沥青路面二维和三维结构分析模型的比较

王威娜，李小飞，徐青杰， 秦 煜， 闫 强

1)重庆交通大学交通土建工程材料国家地方联合工程实验室，重庆 400074； 2)重庆交通大学土木工程学院，重庆 400074；3)中铁二院重庆勘察设计研究院有限责任公司，重庆 400023； 4)广西交投科技有限公司，广西壮族自治区南宁 530021

随着有限元法在道路工程中的不断应用和发展，该方法已成为解决沥青路面力学响应问题的重要工具. 三维有限元模型与实际道路情况较为相符，三维沥青路面分析模型已成为数值模拟的发展趋势. 由于计算模型边界条件复杂，各模型材料参数交互影响，且时间历程较长时，采用三维模型运算效率相对较差，对计算机性能要求较高. 而采用二维有限元模型可显著提高计算效率，应用也较为广泛[1-4].

研究人员基于有限元法建立二维及三维沥青路面分析模型，开展了路面结构层的力学响应规律研究. 已有研究采用二维模型对沥青路面剪应力[1]、垂直位移[2]、竖向应力[2]、水平应力[3]、车辙[1]和裂缝扩展规律[4]等进行了分析. 同时亦有结合三维模型开展了沥青路面剪应力[5]、路表弯沉[6]、水平应力[7]和竖向应力[7]等研究工作. 现有研究结果表明二维有限元模型可揭示沥青路面结构力学响应的一般规律. HUA等[8]开展了二维与三维的车辙预估，结果表明，二维与三维模型的最大永久变形结果相差不大，但该研究中三维模型所采用的荷载形式是条形荷载，与实际三维路面结构的局部面荷载形式有较大区别. 现有研究多是分别建立二维或三维有限元模型进行分析，对比两者关系的研究较少. 个别研究虽对比分析了两种模型的差异，但采用的荷载形式却与实际不同. 现有研究中将三维路面结构简化为二维平面模型的影响尚不明确，尚缺乏二维和三维建模方法对沥青路面力学响应的差异量化.

本研究选取刚性基层、半刚性基层和柔性基层3种典型沥青路面结构，考虑单次静力荷载和动态荷载作用，分别建立二维和三维有限元模型，量化对比两种建模方法对沥青路面位移和应力的影响，针对二维与三维模型的位移和应力进行差异性检验，提出计算不同类型位移和应力的数值模型简化适用性原则.

1 有限元模型的建立

1.1 基本假设

本研究假设：① 各层为均质各向同性材料；② 层间接触面为完全连续；③ 不计各层材料自重.

1.2 计算模型

1.2.1 模型建立

模型尺寸对有限元计算结果有一定影响，现有研究已结合圣维南原理，考虑沥青路面尺寸效应的影响，得到不受边界尺寸效应影响的合理模型尺寸[4,9]. 基于现有研究，二维模型的尺寸选用6 m×3 m[4]，三维模型的尺寸选用6 m×3 m×6 m[9]. 二维和三维模型的边界条件均为：土基底部固定，各层间接触属性设为绑定约束；各个侧面约束其法向位移. 二维模型采用八节点平面应变四边形单元，三维模型采用八节点三维六面体减缩积分单元. 网格划分以荷载作用位置为中心由密到疏逐渐向两边扩展划分.

1.2.2 荷载条件

实际轮载作用于路面的形状较为复杂，可将轮胎作用于路面的形状简化为矩形[5]. 单轮荷载面积简化为0.156 8 m×0.227 7 m，双轮荷载中心的间距为0.319 8 m，二维模型和三维模型的静力荷载形式为单次静力荷载，大小为0.7 MPa[10]. 二维模型动态荷载的加载形式为半正弦波模拟动态荷载[11]，三维模型动态荷载的加载形式为移动荷载.

1.2.3 路面结构与材料参数

为了保证所选的路面结构能较好地反映沥青路面力学特性，结合广东省公路路面典型结构应用技术指南，选取3种典型沥青路面结构进行计算. 主要包括刚性基层、半刚性基层和柔性基层，其结构与材料参数见表1[12].

表1 结构与材料参数

1.3 模型验证与对比

为验证有限元模型的正确性，以肖川等[13]的现场试验为例，选取半刚性基层路面结构，当轴重为10 t，行驶速度为60 km/h时，通过有限元模拟，以面层底面纵向和横向应变的最大值为分析指标，对比有限元数值计算结果与试验数据. 如表2所示，就面层底纵向应变而言，二维与三维模型计算结果和试验数据较为接近. 对于面层底横向应变，三维模型计算结果和试验数据大体一致，二维模型计算结果和试验数据有一定差异. 整体上模型计算结果与试验数据有差异，但均属同一数量级，数值模型基本合理. 模型计算结果的差异是由于三维的路面结构与简化为二维平面模型，导致荷载分布形式的变化，从而引起荷载作用下的应变差异.

为对比二维和三维模型计算结果与基于弹性层状体系理论计算结果的差异，本研究基于弹性层状体系理论，采用BISAR 3.0计算软件，对比弹性层状体系结果和模型计算结果. 由表2可知，二维与三维模型所计算的面层底纵向应变和弹性层状体系计算结果基本相同；对于面层底横向应变，三维模型计算结果和弹性层状体系结果较为相似. 二维模型计算结果约为弹性层状体系结果的6倍，说明三维结构简化为二维平面所导致的荷载变为条形荷载形式，对横向应变的影响较大.

表2 试验数据和模型计算结果及弹性层状体系结果

2 位移对比分析

本研究分别分析了静力荷载和动态荷载作用下3种典型沥青路面结构的位移. 为便于比较，二维与三维模型所选取的分析点为同一位置：横断面上以轮隙中心为起点，沿x轴的各点；深度方向上以轮隙中心为起点，沿y轴的各点.

2.1 竖向位移分析

2.1.1 横断面方向上竖向位移分析

图1给出了静力荷载和动态荷载作用下横断面方向上的竖向位移，其变化规律大致相同. 随着水平距离的增加，竖向位移均呈先增后减趋势. 从轮隙中心到轮载中心，竖向位移有所增加，随着远离轮载中心，竖向位移随之减小. 但二维模型的竖向位移变化量较三维模型大很多.

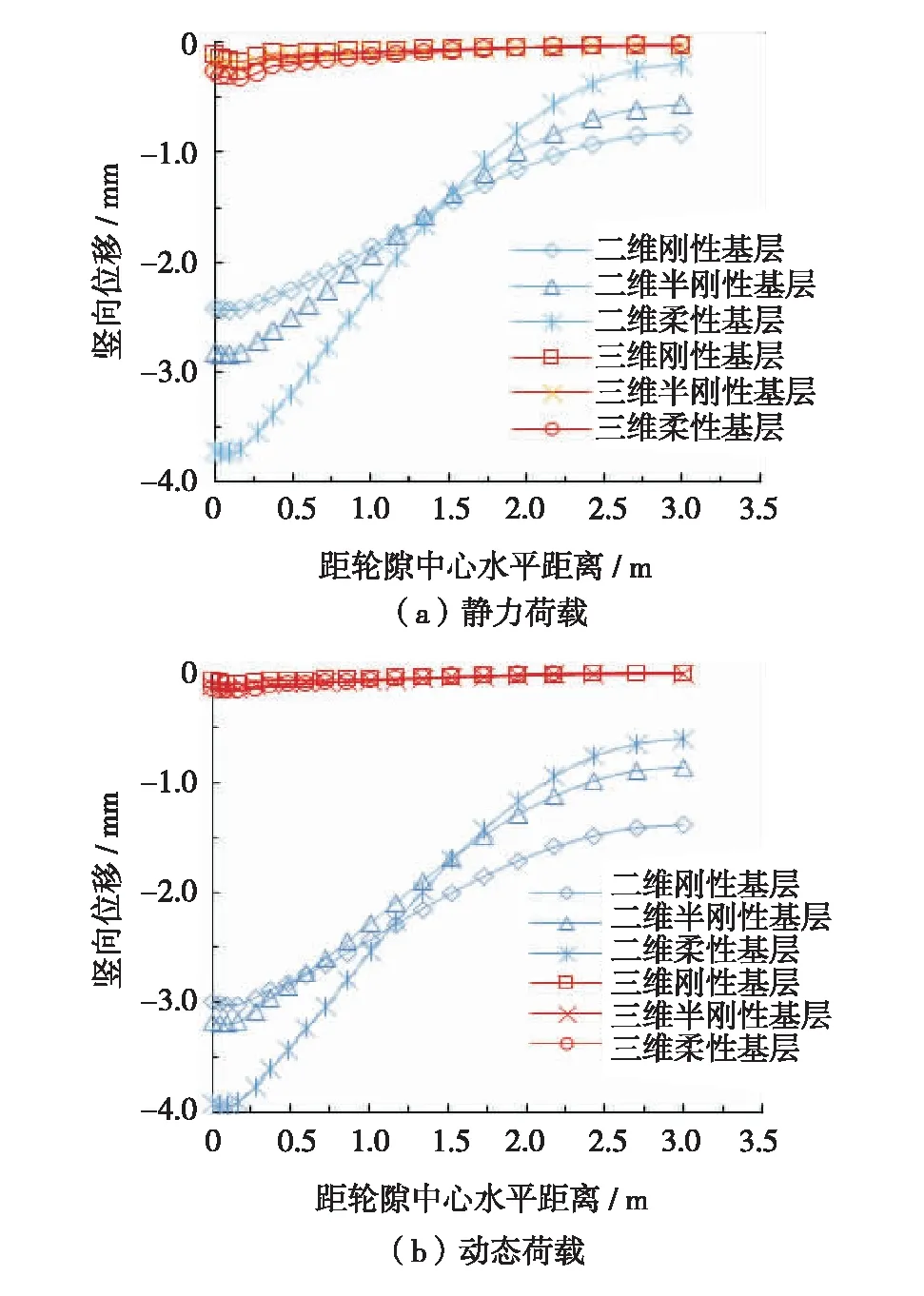
图1 横断面方向上的竖向位移Fig.1 (Color online) Vertical displacement in cross section

为了进一步量化二维和三维模型的差异，以三维模型的竖向位移为x轴，二维模型的竖向位移为y轴，对二维与三维模型竖向位移对比点进行线性拟合．就静力荷载而言，两者竖向位移的线性拟合关系为U竖向2D=15.2U竖向3D，R2=0.73，在进行数据相关分析时，通常要求R≥0.8[14]， 即R2≥0.64．上述拟合模型的R2>0.64， 认为拟合关系模型可靠，可得二维模型竖向位移是三维模型的15.2倍．就动态荷载而言，二维与三维模型竖向位移的线性拟合关系为U竖向2D=29.8U竖向3D，R2=0.41， 难以比较差异. 本研究仅比较两者竖向位移峰值，得到二维模型的竖向位移峰值是三维模型的23.8倍. 所以，无论采用静力荷载还是动态荷载，将三维模型简化为二维模型，会导致轮迹处横断面方向上竖向位移显著增加.

2.1.2 深度方向上竖向位移分析

图2显示了静力荷载和动态荷载作用下深度方向上的竖向位移. 由图2可以看出，静力荷载和动态荷载作用下，二维模型和三维模型的沿深度方向上的竖向位移变化趋势大致相同. 随着深度的增加，荷载作用的影响减小，从面层顶面到底基层底部，竖向位移变形量逐渐减小，在土基区域，竖向位移变形量急剧减小，在土基底部减小到0. 且二维模型的竖向位移变化量比三维模型也大很多.

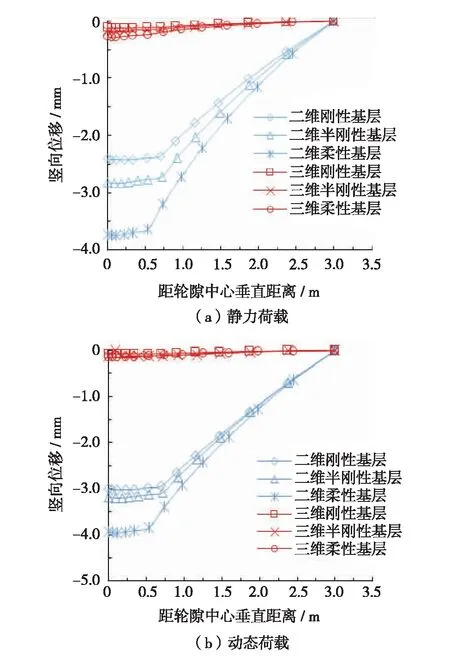
图2 深度方向上的竖向位移Fig.2 (Color online) Vertical displacement in depth direction

同理对二维与三维模型竖向位移对比点进行线性拟合．就静力荷载而言，二维与三维模型竖向位移的线性拟合关系为U竖向2D=16.2U竖向3D，R2=0.84， 所以二维模型的竖向位移是三维模型的16.2倍；就动态荷载而言，二维与三维模型竖向位移的线性拟合关系为U竖向2D=29.7U竖向3D，R2=0.61， 由于R2较小，难以对整个深度范围内的差异进行量化比较，本研究仅比较两者竖向位移计算峰值，计算得到二维模型的竖向位移峰值是三维模型的25.8倍. 所以无论采用静力荷载还是动态荷载，将三维模型简化为二维模型，同样会导致轮迹处的深度方向上竖向位移显著增加.

2.2 水平位移分析

因深度方向上的二维与三维模型的水平位移非常小，均接近0，所以本研究仅对比分析横断面方向上的水平位移. 图3为静力荷载和动态荷载作用下横断面方向上的水平位移. 由图3可知，静力荷载和动态荷载作用下，二维与三维模型的水平位移曲线变化趋势存在差异，从轮隙中心到轮载中心，三维模型的水平位移方向为沿x轴负向，而二维模型水平位移的方向为沿x轴正向，从轮载中心到边界，二维和三维模型的水平位移均是先增后减，且在距轮隙中心1 m处，二维模型的水平位移出现峰值，而在轮载中心附近，三维模型的水平位移出现峰值. 说明将三维路面结构简化为二维平面，将引起水平位移峰值位置的改变.

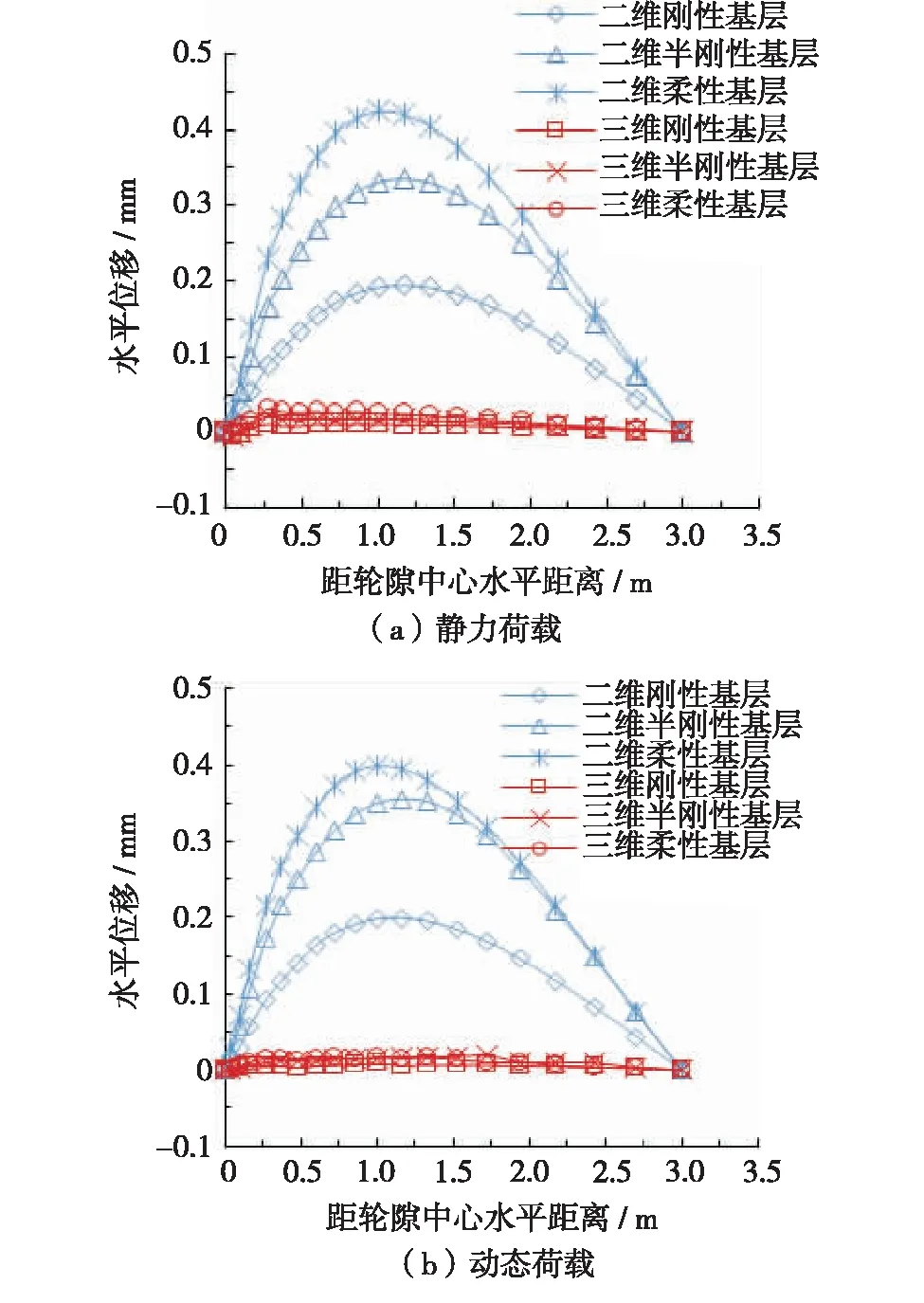
图3 横断面方向上的水平位移Fig.3 (Color online) Horizontal displacement in cross section

同样对二维与三维模型水平位移对比点进行线性拟合．就静力荷载而言，二维与三维模型水平位移的线性拟合关系为U竖向2D=15.4U竖向3D，R2=0.73， 可知二维模型的水平位移是三维模型的15.4倍；就动态荷载而言，二维与三维模型水平位移的线性拟合关系为U竖向2D=21.9U竖向3D，R2=0.88， 即二维模型的水平位移是三维模型的21.9倍. 因此，将三维模型简化为二维模型也会导致轮迹处横断面方向上水平位移显著增加.

3 应力对比分析

本研究还分析了3种典型沥青路面结构的应力，包括垂直应力、水平应力与切应力. 为便于比较分析，二维与三维模型所选取的分析点与位移分析相同.

图4 横断面方向上的垂直应力Fig.4 (Color online) Vertical stress in cross section

3.1 垂直应力对比分析

3.1.1 横断面方向上垂直应力分析

图4给出了静力荷载和动态荷载作用下横断面方向上的垂直应力. 由图4可以看出，静力荷载和动态荷载作用下，二维和三维模型计算所得的垂直应力变化趋势存在差异，垂直应力值均是先增后减，从轮隙中心到轮载中心的区域受轮载作用的影响较大，所以垂直应力值逐渐增大，离轮载中心较远的区域，受轮载作用的影响较小，垂直应力值逐渐减小.

但在轮隙中心处，就静力荷载而言，二维模型的垂直应力表现为拉应力，而三维模型的结果表现为压应力，在距轮隙中心0.45 m处，二维模型的垂直应力表现为拉应力，且二维模型的峰值比三维模型大，就静力荷载而言，二维模型的峰值约为三维模型的1.3倍. 就动态荷载而言，二维模型的峰值约为三维模型的2.5倍.

本研究还对二维与三维模型垂直应力对比点进行了线性拟合. 就静力荷载而言，二维与三维模型垂直应力的线性拟合关系为σ垂直2D=1.2σ垂直3D，R2=0.92， 所以二维模型的垂直应力是三维模型的1.2倍；就动态荷载而言，二维与三维模型垂直应力的线性拟合关系为σ垂直2D=2.6σ垂直3D，R2=0.99， 所以二维模型横断面方向上的垂直应力是三维模型的2.6倍.

图5 深度方向上的垂直应力Fig.5 (Color online) Vertical stress in depth direction

3.1.2 深度方向上垂直应力分析

图5给出了静力荷载和动态荷载作用下深度方向上的垂直应力. 由图5可以看出，静力荷载和动态荷载作用下，二维和三维模型的垂直应力曲线变化趋势有一定的相似性，垂直应力值均是先增后减. 从面层顶面到基层顶面的垂直应力值有所增大，从基层顶面到土基底部，垂直应力值逐渐减小. 但对于静力荷载作用下的二维模型，在轮隙中心处，深度方向上的垂直应力表现为拉应力.

本研究还对两者垂直应力对比点进行了线性拟合. 就静力荷载而言，二维与三维模型垂直应力的线性拟合关系为σ垂直2D=1.49σ垂直3D，R2=0.1， 由于R2较小，本研究仅比较两者垂直应力计算峰值，计算得到二维模型的垂直应力峰值是三维模型的1.8倍；就动态荷载而言，二维与三维模型垂直应力的线性拟合关系为σ垂直2D=3.8σ垂直3D，R2=0.47， 由于R2较小，本研究仅比较两者垂直应力计算峰值，计算得到二维模型的深度方向上垂直应力峰值是三维模型的3.5倍.

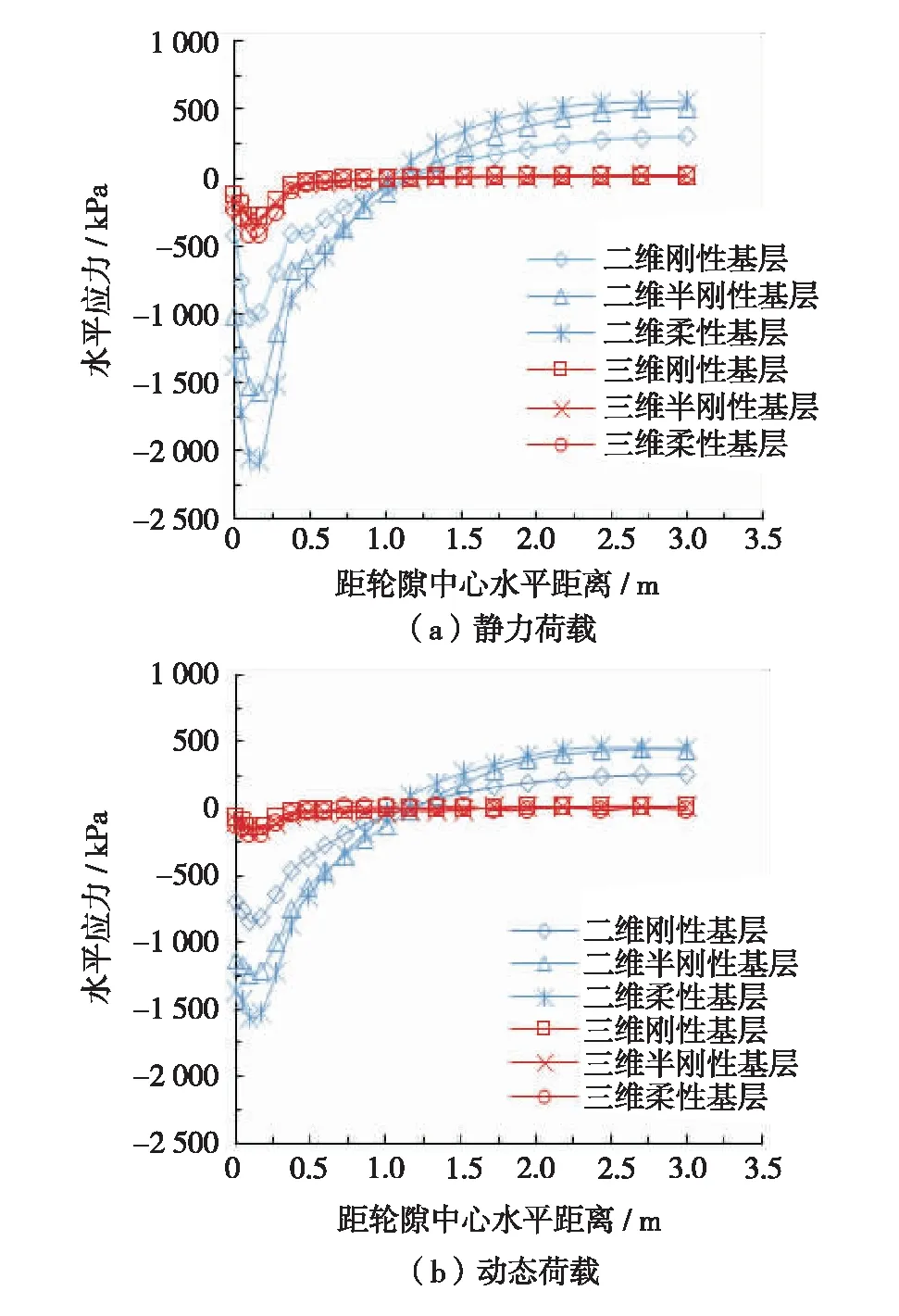
图6 横断面方向上的水平应力Fig.6 (Color online) Horizontal stress in cross section

3.2 水平应力对比分析

3.2.1 横断面方向上水平应力分析

图6显示了静力荷载和动态荷载作用下横断面方向上的水平应力. 由图6可知，二维和三维模型的水平应力变化规律并不完全相同，随着水平距离的增加，水平应力值均是先增后减. 从轮隙中心到轮载中心，水平应力逐渐增大，随着远离轮载中心水平应力随之减小. 但是在距轮隙中心较远区域，二维模型的水平应力表现为水平拉应力.

同理对二维与三维模型对比点进行了线性拟合. 就静力荷载而言，二维与三维模型水平应力的线性拟合关系为σ水平2D=2.1σ水平3D，R2=0.85， 可得二维模型的水平应力是三维模型的5.1倍；就动态荷载而言，二维与三维模型水平应力的线性拟合关系为σ水平2D=9.1σ水平3D，R2=0.86， 所以二维模型的水平应力为三维模型的9.1倍.

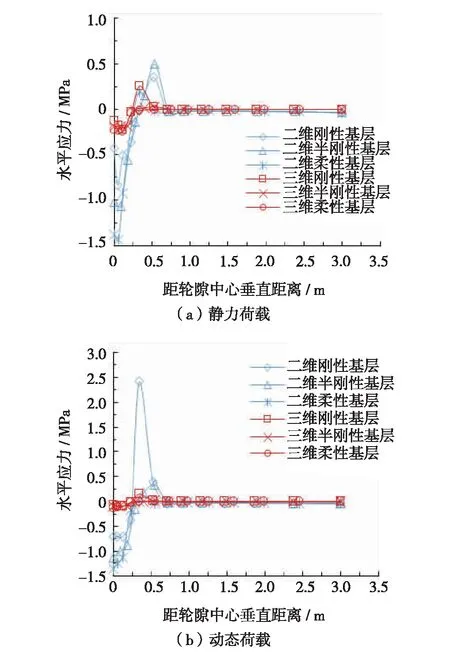
图7 深度方向上的水平应力Fig.7 (Color online) Horizontal stress in depth direction

3.2.2 深度方向上水平应力分析

图7为静力荷载和动态荷载作用下深度方向上的水平应力，其变化趋势大致相同. 从面层顶面到面层底面水平应力均有所增加，均为水平压应力，从基层顶面到底基层底面水平压应力均减小，由压应力变为拉应力，拉应力逐渐增大，在土基区域水平拉应力逐渐减小. 但就动态荷载而言，二维刚性基层路面结构模型的基层底水平应力约为三维模型的16.4倍.

本研究还对二维与三维模型对比点进行线性拟合. 就静力荷载而言，其拟合关系为σ水平2D=4.6σ水平3D，R2=0.85， 二维模型的水平应力是三维模型的4.6倍；就动态荷载而言，其拟合关系为σ水平2D=11.9σ水平3D，R2=0.94， 二维模型的水平应力是三维模型的11.9倍.

图8 横断面方向上的切应力Fig.8 (Color online) Shear stress in cross section

3.3 切应力对比分析

因二维模型仅存在XY面上的切应力，且在深度方向上，二维与三维模型的切应力均非常小，所以本研究仅分析横断面方向上的XY面的切应力. 图8显示了静力荷载和动态荷载作用下横断面方向上的切应力. 由图8可知，静力荷载和动态荷载作用下，二维和三维模型的切应力变化曲线的规律相似，从轮隙中心到轮载中心区域，两者的变化趋势均是先增后减，切应力均是正值，在轮载中心区域某点，减小至零，但在轮载中心区域，就静力荷载而言，二维模型的切应力由正值突变为负值；在距轮载中心较远区域，切应力变为负值，均是先增后减，但在边界处，就动态荷载而言，二维模型和三维模型的切应力由负值突变为正值.

本研究还对二维与三维模型对比点进行了线性拟合．就静力荷载而言，二维与三维模型切应力的线性拟合关系为τ2D=1.1τ3D，R2=0.53， 由于R2较小，本研究仅比较二维模型与三维模型切应力计算峰值，得到二维模型的上下峰值分别是三维模型的2.1与1.5倍，四舍五入近似为2.0倍；就动态荷载而言，二维与三维模型切应力的线性拟合关系为τ2D=2.9τ3D，R2=0.7， 所以二维模型的切应力是三维模型的2.9倍.

4 差异性检验

本研究通过SPSS软件对二维与三维模型的应力、位移进行差异性检验. 同类型二维与三维模型两组数据比较采用双尾t检验，设定P≤0.05时，两组数据存在差异，而P>0.05时，两组数据无显著差异. 检验结果如表3.

当P>0.05时，静力荷载作用下，二维模型与三维模型在横断面方向上垂直应力和切应力的差异不显著，二维模型与三维模型的比值分别为1.2和2倍，这从侧面说明了模型所得比较倍数的正确性. 统计分析表明，动态荷载作用下，二维模型与三维模型在深度方向上水平应力的差异也不显著，但二维模型与三维模型的比值却相对较大，为11.9倍. 结合图7(b)可知，二维模型与三维模型所得水平应力峰值与应力分布特征有差异，但大多数的点差异不明显，所以P>0.05， 统计学上差异不显著，但其比例倍数较大. 所有类型的两组位移数据所对应的P均小于0.05，这说明在应用二维和三维模型计算所有类型的位移时，两个模型结果具有较大差异，这与数值计算所得倍数都超过15的结果相符. 如表3所示，统计学计算所得差异不显著组别的倍数差异均小于2倍，亦说明数值计算所得倍数与统计学结果相一致. 因此，结合统计学上差异不显著组别得到，在分析静力荷载作用下横断面方向上垂直应力和切应力时，可将三维路面结构简化为二维平面，而在分析其他类型位移、应力时，不建议将三维路面结构简化为二维平面.

从荷载作用方面分析，实际三维路面结构为局部面荷载形式，而将三维路面结构简化为二维平面模型导致二维平面模型的荷载实际为条形荷载，这与实际三维路面结构荷载形式有较大差异，这两类模型计算得出的力学响应存在差异也与理论分析相符.

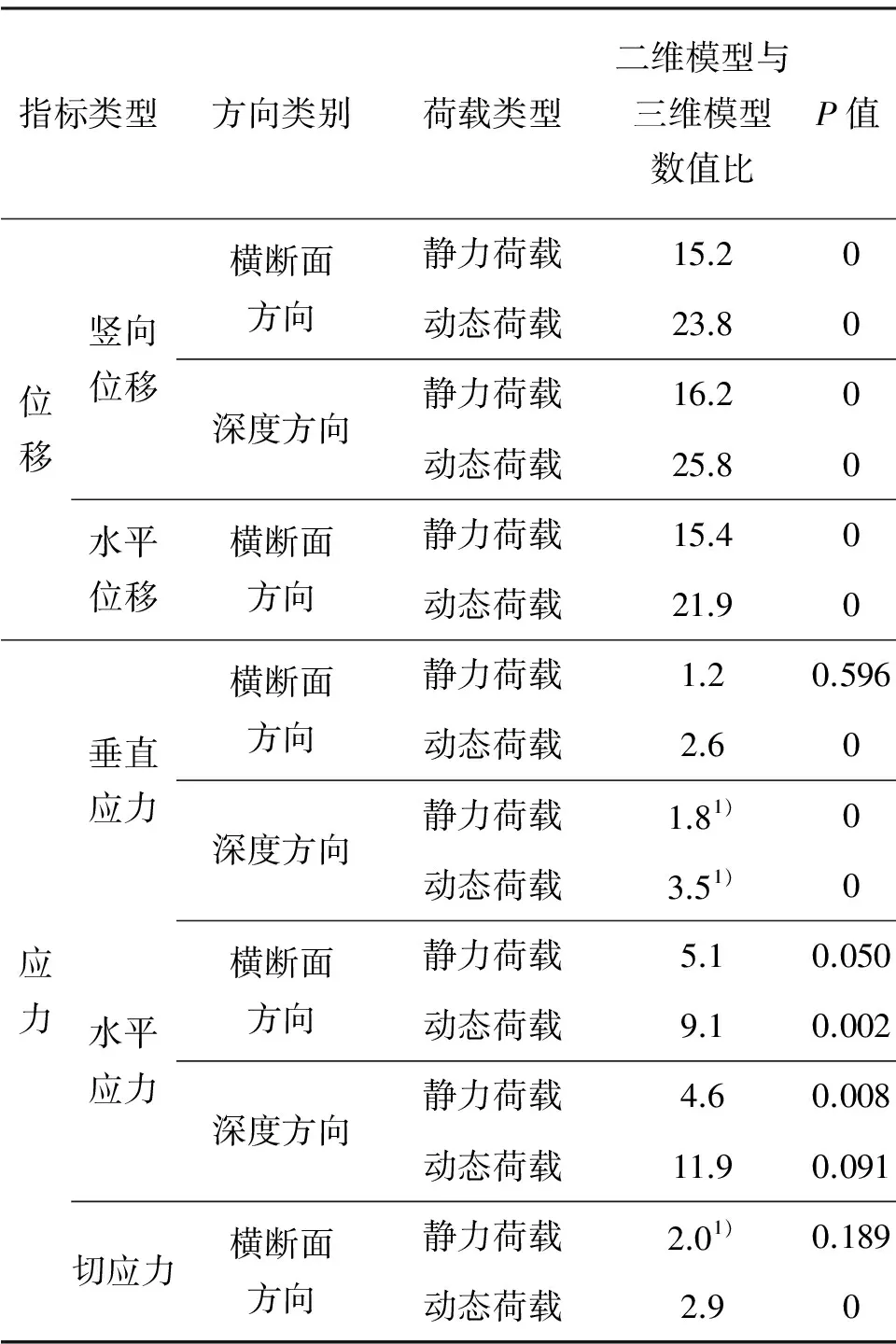
表3 二维与三维模型计算结果比较

1)为峰值比值

5 结 论

1)三维模型简化为二维模型时，在静力荷载作用下二维模型较三维模型的位移会显著增加，可达15倍以上，在动态荷载作用下位移增加更甚，达22倍以上.

2)三维模型简化为二维模型时，两个模型计算所得应力峰值出现位置有所差异，其横断面及深度方向上的不同类型应力比值差异相对较大，应力增加倍数相对位移增加均较小，静力荷载作用下二维模型应力均近似小于三维模型的5倍，动态荷载作用下二维模型应力不大于三维模型的12倍.

3)在分析静力荷载作用下横断面方向上的垂直应力和切应力，可将三维路面结构简化为二维平面. 而在分析其他类型位移、应力时，不建议将三维路面结构简化为二维平面.

4)沥青路面的力学响应受到荷载作用形式、温度等的影响，可进一步考虑疲劳荷载作用情况及温度变化情况，从而更加全面的把握二维和三维沥青路面结构模型的应力应变差异.

引文：王威娜，李小飞，徐青杰，等．沥青路面二维和三维结构分析模型的比较[J]. 深圳大学学报理工版，2018，35(1)：39-47.

/

[1] 彭妙娟, 赵文宣. 层间接触对沥青路面抗车辙性能的影响[J]. 公路交通科技, 2016,33(7):1-6.

PENG Miaojuan, ZHAO Wenxuan. Influence of interlayer contact on anti-rutting performance of asphalt pavement[J]. Journal of Highway and Transportation Research and Development, 2016, 33(7): 1-6.(in Chinese)

[2] 马国存. 竖向移动荷载作用下沥青路面结构体系响应研究[D]. 长沙：中南大学, 2009.

MA Guocun. Study on response of asphalt pavement structure system under vertical moving load[D]. Changsha: Central South University, 2009.(in Chinese)

[3] BUTTLAR W G. Application of graded finite elements for asphalt pavements[J]. Journal of Engineering Mechanics, 2006,132(3):240-249.

[4] 金光来. 基于扩展有限元的沥青路面疲劳开裂行为的数值研究[D]. 南京：东南大学, 2015.

JIN Guanglai. Numerical analysis of fatigue crack growth in asphalt pavement based on extended finite element model[D]. Nanjing: School of Transportation Southeast University, 2015.(in Chinese)

[5] 胡小弟, 孙立军, 刘兆金. 沥青路面非均布荷载下层间接触条件不同时力学响应的三维有限元分析[J]. 公路交通科技, 2003,20(3): 1-4.

HU Xiaodi, SUN Lijun, LIU Zhaojin. Stress response analysis of asphalt pavement with different interlayer touch types under non-uniform distributed tire pressure through 3D finite element method[J]. Journal of Highway and Transportation Research and Development, 2003, 20(3): 1-4.(in Chinese)

[6] 侯 静. 基于动荷载仿真的路面结构响应分析[J]. 河北工业大学学报, 2016,45(1): 114-118.

HOU Jing. Pavement structural mechanics based on the dynamic load simulation[J]. Journal of Hebei University of Technology, 2016, 45(1): 114-118.(in Chinese)

[7] 谢水友, 郑传超. 轮胎接触压力对沥青路面结构的影响[J]. 长安大学学报自然科学版, 2004,24(1): 12-16.

XIE Shuiyou, ZHENG Chuanchao. Effects of tire contact pressure on asphalt pavement structure[J]. Journal of Chang’an University Natural Science, 2004, 24(1): 12-16.(in Chinese)

[8] HUA E J, WHITE P A H T. A study of nonlinear tire contact pressure effects on HMA rutting[J]. International Journal of Geomechanics, 2002, 2(3):353-376.

[9] 李新贺. 沥青路面不同层间接触状态对路面结构受力的响应研究[D]. 西安：长安大学, 2012.

LI Xinhe. Merchanical response of asphalt pavement under different contact condition among interfacials[D]. Xi’an: Chang’an University, 2012.(in Chinese)

[10] 黄仰贤. 路面分析与设计[M]. 北京：人民交通出版社, 1998.

HUANG Yangxian. Pavement analysis and design[M]. Beijing: People Communications Press,1998.(in Chinese)

[11] 陈洪兴. 基于路面平整度时域模型的沥青路面车辙计算方法研究[D]. 重庆：重庆交通大学, 2008.

CHEN Hongxing. Study on the method to calculate the rutting of asphalt pavement based on the time domain model of roughness[D]. Chongqing: Chongqing Jiaotong University, 2008.(in Chinese)

[12] 广东省公路路面典型结构应用技术指南[Z]. 广州：广东省交通运输厅，2008.

Guangdong Province highway pavement typical structure application technical guide[Z]. Guangzhou: Guangdong Provincial Department of Transportation, 2008.(in Chinese)

[13] 肖 川, 邱延峻, 黄 兵. 基于车辆加载试验的沥青路面动力响应分析[J]. 公路交通科技, 2014,31(12): 12-19.

XIAO Chuan, QIU Yanjun, HUANG Bing. Analysis on dynamic response of asphalt pavement based on vehicle loading test[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 12-19.(in Chinese)

[14] 谢 平, 唐亚松, 李彬彬， 等. 基于相关系数的水文趋势变异分级方法[J]. 应用基础与工程科学学报, 2014, 22(6):1089-1097.

XIE Ping, TANG Yasong, LI Binbin, et al. Classification method of hydrological trend variation based on correlation coefficient[J]. Journal of Basic Science and Engineering, 2014, 22(6): 1089-1097.(in Chinese)