基于小波包滤波列车自动驾驶的研究

何 晖， 唐 涛

（北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

ATC作为保障列车运行安全和效率、调节列车运行的关键设备。目前CBTC列车控制系统核心工作就是通过由地面设备、车载设备和控制中心组成的控制系统来完成对列车整个运行过程的控制［1-5］，因此对列车运行控制系统进一步的研究具有重要的意义。

本文通过分析列车停车制动特性，求解出列车ATO制动过程中的制动模型［6-8］，从而便于采用迭代学习的方法对输入初始值进行调节，进而针对列车停车精度不高、运行环境复杂、干扰因素多等问题，提出一种基于小波包滤波和迭代学习相结合的列车自动驾驶控制系统。

由于列车控制器在跟踪曲线过程中，速度数据的采集往往夹杂着噪声的干扰。为能够有效去除噪声干扰，更为准确地获取列车速度，避免造成过于严重的测量误差，应用小波包滤波方法去除速度测量过程中的噪声干扰，进而采用迭代学习控制器实现列车的精确停车［9-12］。实验表明，此方法能够更为精确的实现列车停车控制，且迭代次数少，效率高。

1 列车运行与制动模型

1.1 列车运行过程

ATO的关键工作就是对列车运行速度进行实时自动调整，实施平稳快速地起动，确保平稳地行进于区间，停靠于车站正确位置，完成高质量的自动驾驶。同时，ATO相关操作由ATP实施防护，其功能可分3个阶段。

（1）车站发车

如图1所示的a、b阶段，车站发车功能就是给列车提供加速度，使列车从静止状态加速到目标速度。在保障乘客舒适性的前提下，ATO根据预定的目标速度调节加速度，当列车达到目标速度后以及接受命令的时候，及时调整列车加速度，当列车到达限速时，控制列车进入正常的区间运行阶段。

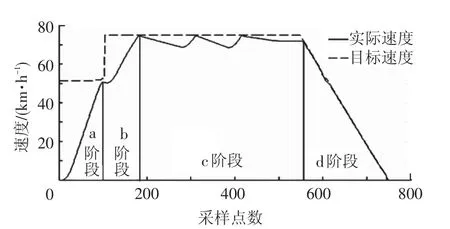
图1 区间运行图

（2）区间速度跟踪

如图1所示的c阶段，区间列车运行速度控制功能就是控制列车在区间正常行车。列车运行控制系统根据线路情况、列车具体位置，以及各种限制条件所计算的速度向ATO速度控制器提供一个参考目标速度，整个线路的参考目标速度最后形成位移-速度曲线。整个区间运行中，ATO控制列车跟踪目标速度，保证列车安全准点到达。

（3）车站精确定点停车

如图1所示的d阶段，车站定点停车功能主要是为了保证乘客上下车便利，由于目前城市轨道系统普遍安装了安全门，如果列车停车位置不恰当，会导致列车车门与安全门存在较大的误差，不便于乘车。列车到站停车时，ATO根据停车点、实际运行速度、列车当前位置，以及其他的一些因素计算出目标制动曲线，按照最优的控制策略保障列车停靠在目标点，以保证误差在30 cm以内。

1.2 制动模型

车载ATO控制从指令发出到指令执行，该过程可以用方程来描述［13-16］，即

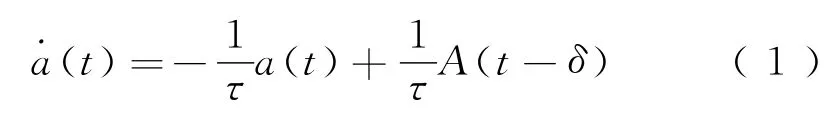
式中：a（t）为制动加速度，由制动系统产生；A（t）为目标加速度；τ为系统响应常数；δ为传输延时。由式（1）可知，列车停车过程为典型的时滞过程，因此整个系统可以用一个纯时滞一阶惯性环节来近似描述其中的延时特性，可描述为

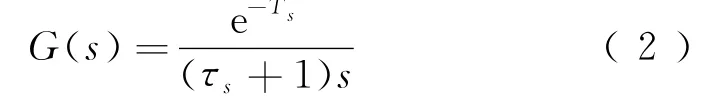
整个车载ATO制动模型的控制框图见图2。

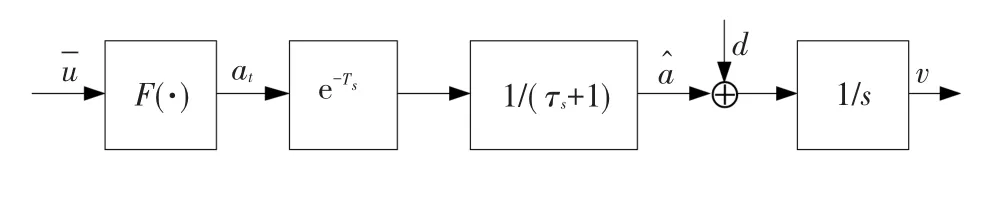
图2 带有延时和上升环节的制动模型

图2中对于无级调速系统而言，F（·）表示连续函数；而对于分级调速系统而言，F（·）表示不同档位与和目标加速度间的函数关系。因此，加速度at可以被认为是经过转换后的实际输入加速度，而^a为经过延时环节和上升环节后的加速度，d为由坡度偏差等造成的干扰。

2 基于小波包的列车自动驾驶控制系统速度滤波

在加速度、速度采集、量测过程中往往伴随着大量的噪声污染与干扰，这会严重影响控制器的性能，甚至导致控制器失灵而无法进行有效的控制［17］。为能够有效的去除噪声干扰，采用基于辅助模型来获取更好的参数的方法，从而获取更好的控制效果，这是工程实践中常用的方法。滤波辅助模型能够将参数数据中的噪声干扰大幅度降低，甚至滤除，从而获取更为接近真值的参数数据，这能有效的避免参数计算引进的测量误差。常用的滤波辅助模型有基于FIR、IIR以及小波包等的信号处理方法。

小波包是一种比小波更为细致、精确的信号分析与处理的方法［18］，它能够对频带进行多分辨率的划分，且能够针对小波分析中不做更加细微划分的高频子带数据做进一步分析处理，依据被处理信号获取特征数据。小波包能够自适应地选取对应子带，使处理后的信号的频谱能够匹配原始信号数据，从而获取更高的时-频分辨率［19］。因此小波包获取更广泛应用场景，在各个领域中都能够融合。小波包3层分解见图3。

图3 小波包三层分解

式中：hl－2m、gl－2m为系数序列，且两系数存在正交关系。

图4针对列车的运行速度，采用db08小波基，用3层小波包对含有白噪声的列车速度数据进行分解并获取各个分辨率下的小波系数数据。

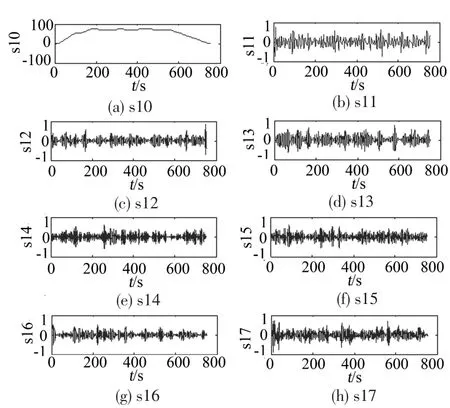
图4 列车速度经过小波包3层分解的8个尺度下的数据

s10、s11、s12、s13、s14、s15、s16、s17代表列车速度经过小波包3层分解的8个尺度下的数据，由于列车速度的变化频率主要集中在低频部分，通过列车速度能量谱分析可知，列车速度能量主要集中在0～20 Hz之间。因而可以将高频部分s11、s12、s13、s14、s15、s16、s17置为零，只保留s10信号。本文采用北京亦庄线某站间列车运行数据为样本，滤波后的列车数据与滤波前的列车数据对比见图5。

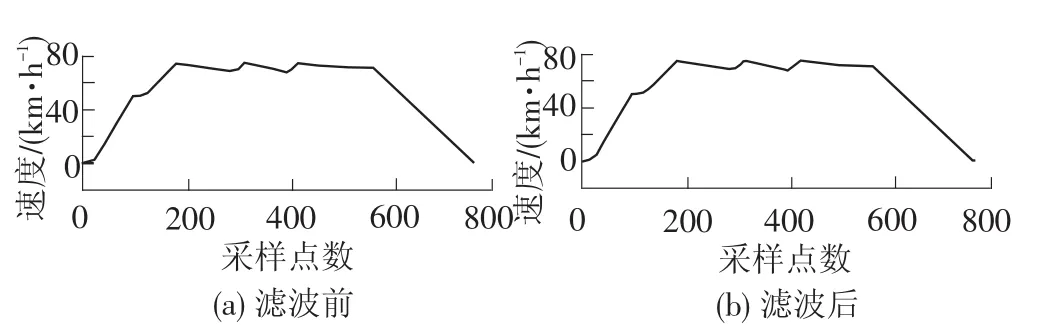
图5 滤波前后的列车速度曲线对比

仿真实验结果表明，小波包滤波器能够有效滤除列车速度中的噪声污染带来的数据干扰，从而获取更加精确的速度数据，进而为后续跟踪速度曲线，确定制动点的起始速度打下良好的数据基础。

3 基于小波包滤波技术停车控制策略

确定起始制动点是所有终端停车控制方法研究的核心问题。为了有效解决此问题，提出一种小波包滤波与“交点法”相结合的起始制动点确定方法。由于含噪声的速度数据直接作为控制器的输入会造成控制器性能下降。因而，首先要获取可靠的速度数据作为控制器的输入，这就需要将采用小波包预处理后的速度数据作为控制器的输入数据，然后由下式估算停车时间

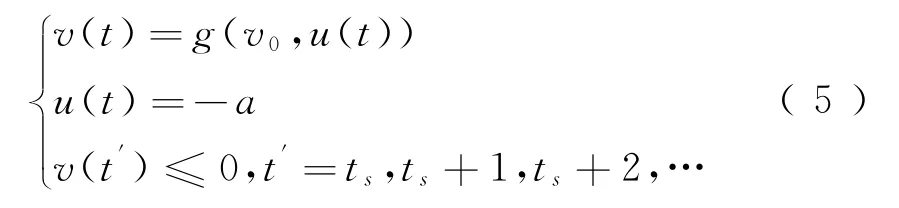
式中：v0为经过小波包预处理后的列车运行初速度；u（k）为施加列车减速度，在此假设该控制输入为负数－a；g（v0，u（k））为经过小波包预处理后速度v在控制作用下的响应函数；ts为列车从制动开始到停稳整个过程中所用的时间。继而通过距离计算，得到列车运行的目标距离。

为了保证通用性，这里令sobj＝f（v0，t*s），令｛st，vt｝为列车在t时刻的状态量，t*为当v＝vt时由方程组所确定的ts，此后，只需要判断st和f（vt，t*）大小来判断是否“相交”。如

在实际中，可以取一个较小的数ε，ε的取值与采样周期，停车精度等因素相关。判断列车是否起动制动确定根据为

4 实验结果

为验证提出控制方法的有效性，采用前所示的制动模型利用表1的仿真参数对本系统模型进行仿真验证与测试。

表1 仿真参数

基于表1的参数，列车运行时的仿真结果见图6。

从图6可知，当迭代次数为5时，列车的停车误差已经达到最小，实际测得停车误差0.1 m，小于0.3 m，达到实际的停车误差标准。

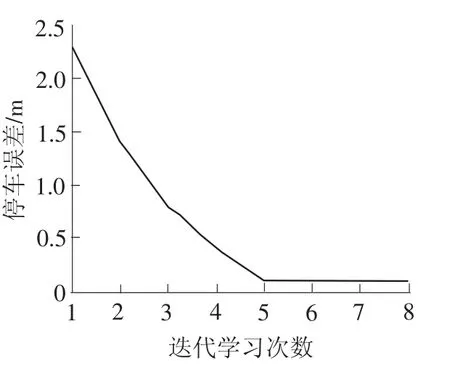
图6 列车运行时的仿真结果

当改变ε时，停车误差和迭代次数都会发生变化，见表2。

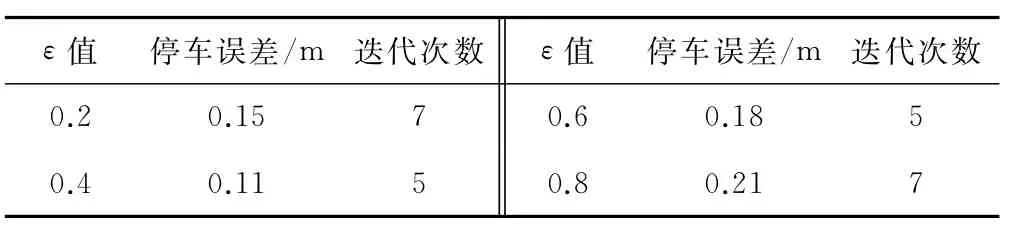
表2 不同ε值的实验结果

表2中当选取ε值为0.4时，停车误差为0.1 m，迭代次数5，要比取值0.2，0.6与0.8要好。从数据的变化趋势来看，ε值为0.4更适合系统模型。

不经过滤波直接把采集到的速度数据作为“相交法”迭代学习的输入，由于含有噪声的干扰，会对实验结果产生不良的影响。列车速度不经过滤波与经过小波包滤波的迭代控制实验结果见表3。

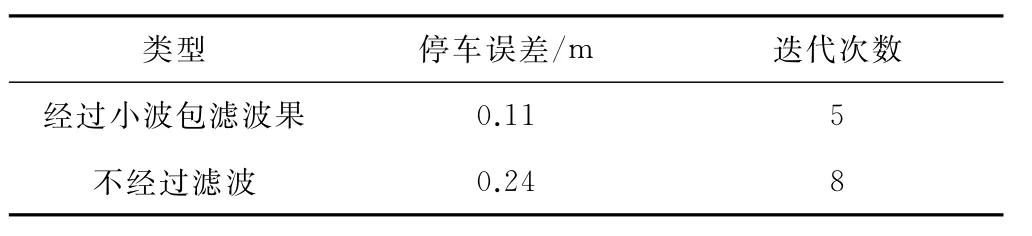
表3 是否经过小波包滤波的实验结果

由表3可见，不经过滤波的停车误差是0.24 m，迭代次数8次，而经过小波包滤波的停车误差是0.11 m，迭代次数5次，实验结果误差大0.13 m，迭代次数也多3次。因此选用小波包与“相交法”相结合的方法具有较好的停车控制性能。

5 结束语

本文针对列车停车精度不高、运行环境复杂、干扰因素多等特点和因素，首先描述了列车的行进过程与制动模型，然后依据列车的行车速度曲线和停车速度位移曲线，采用小波包滤波与迭代学习“交点法”相结合构建了列车行车控制系统。采用小波包方法能够有效滤除数据采集、量测过程中的外部噪声，提高列车速度采集的精度，从而避免噪声扰动，使得列车速度跟踪更为精确，同时也获取了迭代过程中更加稳定、准确的速度初始值。采用迭代学习“交点法”能够有效地将列车运行速度曲线平滑地切换到列车停车速度曲线，从而避免了列车为了单纯跟踪列车行进速度曲线多次切换制动器，同时也简化控制过程并且提高列车行进过程的舒适度。仿真结果表明，采用小波包与“相交法”相结合的方法经过5次左右的迭代学习，停车精度达到0.3m以内，满足实际的列车停车控制要求。

［1］郜春海，陈德旺.基于模型选择和优化技术的自动驾驶制动模型辨识研究［J］.铁道学报，2011，33（10）：57-60.

GAO Chunhai，CHEN Dewang.Study on ATO Braking Model Identification Based on Model Selection and Optimization Techniques［J］.Journal of the China Railway Society，2011，33（10）：57-60.

［2］冷勇林.基于专家经验和机器学习的列车智能驾驶算法研究［D］.北京：北京交通大学，2013.

［3］赵文天，郜春海.城轨列车自动驾驶广义预测控制器的算法研究［J］.计算机工程与应用，2015，51（21）：259-264.

ZHAO Wentian，GAO Chunhai.Study of ATO Control Algorithm in Urban Rail Transit Based on Generalized Predictive Control［J］.Computer Engineering and Applications，2015，51（21）：259-264.

［4］张梦杨.基于滑模的列车运行速度跟踪控制研究［D］.北京：北京交通大学，2015.

［5］杨展.城轨列车自动调整系统模型与算法研究［D］.成都：西南交通大学，2012.

［6］吴鹏.城轨列车精确停车算法研究［D］.成都：西南交通大学，2012.

［7］曾强.城市轨道交通停车算法研究［D］.北京：北京交通大学，2015.

［8］王青元，吴鹏，冯晓云，等.基于自适应终端滑模控制的城轨列车精确停车算法［J］.铁道学报，2016，38（2）：57-63.

WANG Qingyuan，WU Peng，FENG Xiaoyun，et al.Precise Automatic Train Stop Control Algorithm Based on A-daptive Terminal Sliding Mode Control［J］.Journal of the China Railway Society，2016，38（2）：57-63.

［9］GIUSEPPE V，SILVIA C，TOMMASO D.Automatic Detection of Surface EMG Activation Timing Using a Wavelet Transform Based Method［J］.Journal of Electromyography and Kinesiology，2010，20（4）：767-772.

［10］SILVIA C，TOMMASO D，STEFANO P.Optimal Rejection of Movement Artefacts from Myoelectric Signals by Means of a Wavelet Filtering Procedure［J］.Journal of Electromyography and Kinesiology，1999，9（1）：47-57.

［11］GABRIEL K，BRANI V.The Partitioning of Attached and Detached Eddy Motion in the Atmospheric Surface Layer Using Lorentz Wavelet Filtering［J］.Boundary-layer Meteorology，1996，77（2）：153-172.

［12］TAE W J，SEOUNG B K.Time Series Forecasting Based on Wavelet Filtering［J］.Expert Systems with Applications，2015，42（8）：3868-3874.

［13］王呈，唐涛，罗仁士.列车自动驾驶迭代学习控制研究［J］.铁道学报，2013，35（3）：48-52.

WANG Cheng，TANG Tao，LUO Renshi.Study on Iterative Learning Control in Automatic Train Operation［J］.Journal of the China Railway Society，2013，35（3）：48-52.

［14］王呈.列车自动驾驶控制模型参数辨识及其应用［D］.北京：北京交通大学，2014.

［15］贺广宇.基于LQR的列车精确停车控制算法研究［D］.北京：北京交通大学，2009.

［16］张强.基于遗传算法的列车自动驾驶系统研究与实现［D］.北京：北京交通大学，2008.

［17］YOUNGMIN S，SUNGWONK，OZGUR K，et al.Daily Water Level Forecasting Using Wavelet Decomposition and Artificial Intelligence Techniques［J］.Journal of Hydrology，2015，520（1）：224-243.

［18］ACHILLEAS S F，ARNE S，REINER H.Wavelet Transform Filtering and Nonlinear Anisotropic Diffusion Assessed for Signal Reconstruction Performance on Multidimensional Biomedical Data［J］.IEEE Transactions on Biomedical Engineering，2001，48（2）：213-222.

［19］MARIE F，KAI S.Wavelet Transforms and Their Applications to M HD and Plasma Turbulence［J］.Journal of Plasma Physics，2015，81（6）：1-48.