铁路轨道近景影像特征的自动识别与无缝拼接方法

陈 强， 赵晶晶， 彭卫平， 佘 毅， 刘丽瑶， 杨莹辉

（1.西南交通大学 测绘遥感信息系，四川 成都 610031；2.四川省测绘产品质量监督检验站，四川 成都 610041）

高速铁路轨道的高平顺性与高稳定性是列车长期安全运行的重要地面基础，而轨道直接承载车轮并引导列车运行，如果轨道的几何平顺性不良，将引起机车车辆剧烈振动，轮轨作用力成倍增加，严重危害轨道和机车车辆部件，甚至导致脱轨事件。为确保高速行驶列车的平稳性和舒适性，必须加强对铁路轨道几何状态的检测和维护，确保轨道状态具有长期的高平顺性［1-2］。

随着我国高速铁路运营里程和在建规模的不断扩大，快速准确地完成大规模轨道检测将成为一项具有挑战性的工作。而将近景摄影测量技术引入轨道几何状态检测，通过数码相机获取数字影像，采用非接触测量方式，可快速、高效地获取大面积连续的长轨道影像数据。数字图像具有信息量大且易于存储、计算机处理自动化程度高等显著优势，是一种具有应用潜力的轨道检测新方法［3-4］。

轨道影像的准确匹配是近景摄影测量检测轨道几何平顺性的重要技术环节，可为轨道影像的精确定向与建模提供大量分布均匀的同名点［5］。高速铁路轨道近景影像上有钢轨、轨道板及扣件等铁路构筑物，图像纹理特征差异小且灰度变化不显著，灰度值的相似程度比较高，尤其是钢轨的颜色基本保持同一色调，且影像数据量大，因此需要探索一种适合于高速铁路轨道近景影像的准确、快速匹配算法。

本文试验采用ORB（Oriented FAST and Rotated BRIEF）算法对高速铁路轨道近景影像进行特征点检测与匹配，ORB算法具有计算性能高、数据处理实时性和图像旋转不变性［6］，对抗噪性能也有较好表现，可快速、准确地匹配出大量同名点。采用ORB算法对影像进行特征点检测，以最近邻距离与次近邻距离的比值及随机抽样一致性RANSAC（Random Sample Consensus）方法完成同名点的匹配，根据匹配的同名点为基础进行轨道影像的拼接，通过采集杭甬客运专线无砟轨道的影像进行实验与对比分析。

1 ORB算法提取特征点

ORB算法首先使用FAST算法检测得到大量的特征点，之后采用Harris算法过滤得到稳定的特征点，然后通过Hu矩为特征点确定主方向，最后采用BRIEF算法为特征点建立描述符，使特征点具有旋转不变性。ORB算法提取特征点不仅提高了特征点的稳定性，增加了特征点的旋转不变性，而且简化了描述向量的构建过程，缩短了后续特征点匹配所用的时间。

1.1 FAST算法检测特征点

ORB算法采用FAST算法作为特征点的检测核，检测获得特征点。FAST算法定义的特征点是当某个像元异于其周围足够数量的像元时，该像元被认定为这个区域的一个特征点［7］，在灰度图像中表现为该像元灰度值大于或者小于它附近一定数量的像元灰度值，见图1。

在图1中，任取一个像元P为中心，在半径为3个像元的圆环上共有16个像元，按照角点响应函数式（1），圆环上的每个像元存在darker、similar和brighter共3种状态，即

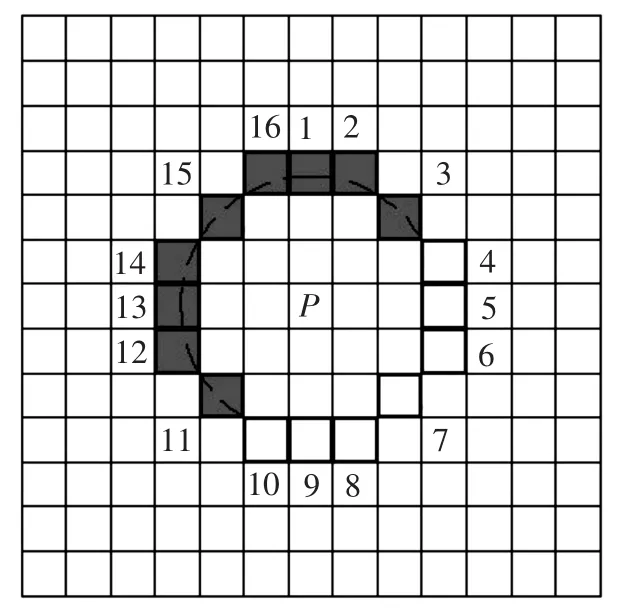
图1 FAST算法定义的特征点

式中：Ip为中心像元的灰度值；Ip→x为圆环上16个像元中某个像元的灰度值；t为一个适当的阈值。假设在圆环上存在1个连续的圆弧，该圆弧上的像元全部处于darker状态或者brighter状态，则中心像元就是1个特征点。其中圆弧的长度可以选择9、10、11、12个像元，考虑到提取特征点的可靠性，通常选择9个像元构成的圆弧，如图1中灰色部分所示的9个像元。

采用FAST算法获得的特征点会存在聚簇现象，需采用非极大值抑制方法去除局部冗余，使保留下来的特征点在局部区域最优。使用非极大值抑制前，需要寻找每个特征点的最大阈值tmax，也就是使中心像元成为特征点的最大临界值，超过该临界值中心像元将不再判定为特征点。通常在判定中心像元为特征点后，采用二分查找法在t与最大灰度值255之间寻找该特征点的临界阈值tmax。确定每个特征点的临界阈值tmax后，在特征点的3×3邻域内，进行非极大值抑制运算，如果中心特征点的临界值大于其他特征点的临界阈值，则保留中心特征点，反之则舍弃，从而得到局部最优的特征点。

1.2 Harris算法过滤特征点

FAST算法检测的特征点沿着影像中地物的边缘分布较多，这类特征点实际上是边缘点，其稳定性相对较差。采用Harris算法的角点响应函数计算特征点的响应值［8］，作为特征点稳定性的评价测度，用以得到稳定的特征点。

Harris算法检测特征点，采用一个窗口在图像I（x，y）上进行局部的微小移动［u，v］，灰度的改变量为

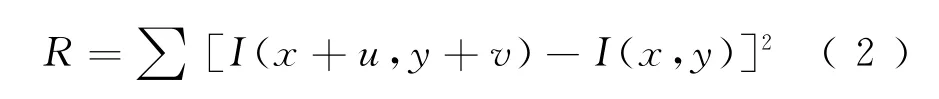
由二元函数的泰勒公式

得到Harris算法的角点响应函数R为

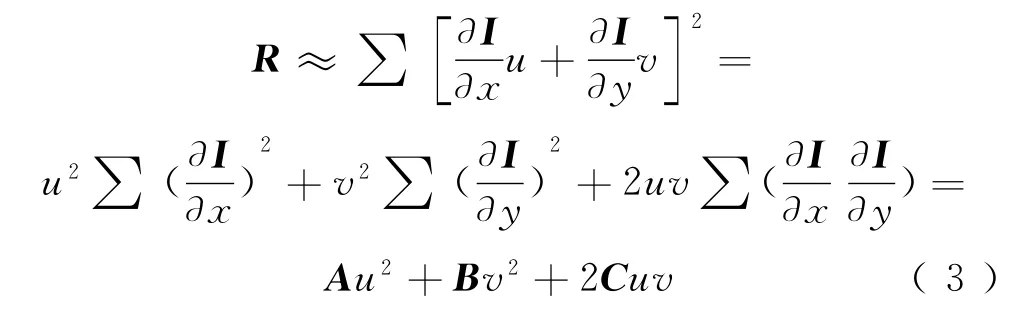
式中：

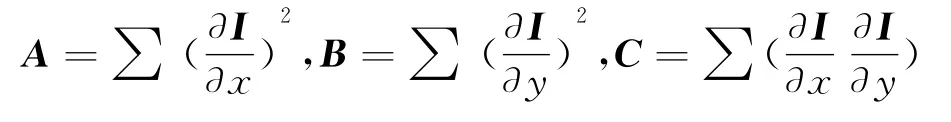
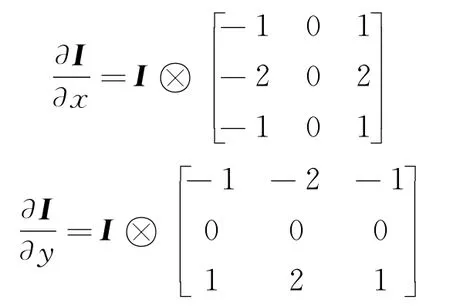
则式（3）用矩阵形式表示为

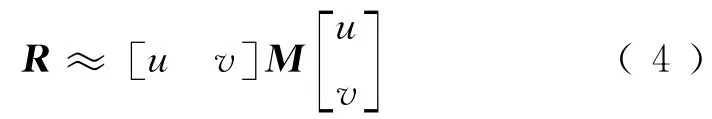
式中：det为矩阵的行列式；tr为矩阵的迹（矩阵对角线元素的和）；k为经验值，一般取0.04～0.06。

由于Harris算法只考虑平坦区域、边缘以及角点3种情况的响应值，其在角点处的响应值最大。因此使用Harris角点响应函数计算每个FAST算法检测的特征点在其邻域内的响应值，按照特征点响应值的大小进行降序排列，截取计划数量的前N个点作为最终稳定的特征点，避免了让所有的候选特征点参与匹配计算，降低误匹配率，节省匹配时间。

1.3 Hu矩确定特征点主方向

目前得到的特征点没有设定主方向，该类特征点不具备旋转不变性，Rosin利用图像的几何矩给特征点提供一个确定主方向的方法［9］，而几何矩由Hu在1962年提出［10］，对于离散状态下的数字图像I（x，y）的（p＋q）阶几何矩定义为

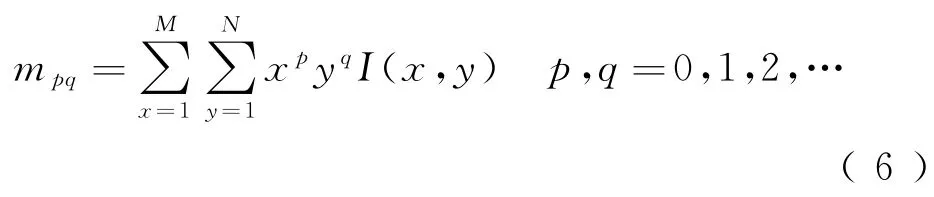
图像不同阶的几何矩表示了图像亮度分布的不同空间特性。零阶几何矩m00代表1幅图像的总亮度；一阶几何矩m10、m01代表图像关于x轴和y轴的亮度矩［11］。由图像的零阶矩和一阶矩得图像I（x，y）的矩心（¯x，¯y）的表达式为

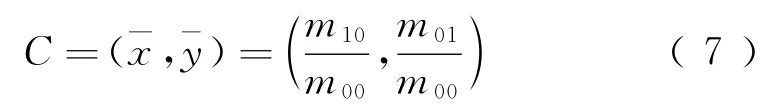
为了保证主方向具有各向同性，以特征点为圆心O，建立一个半径为r个像元的圆，计算圆的矩心C，由于圆心和矩心确定了一个方向OC，则特征点的主方向为

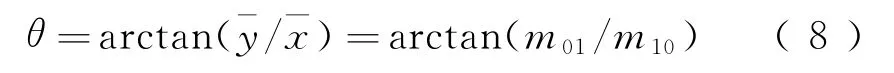
式中：θ的取值范围是（－π，π］。

1.4 建立BRIEF描述符

ORB算法采用BRIEF为特征点建立描述符，使特征点具有旋转不变性。BRIEF是Calonder在2010年提出的一种基于比较的描述向量［12］，该算法对特征点周围指定区域内的多个像素点对进行二值化判断（即0或1的判断），建立一个由二进制数表示的描述向量。在特征点周围S×S大小的图像块中定义1个像素点对p的τ检测

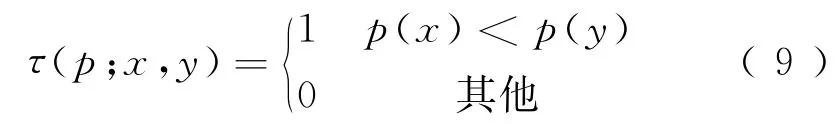
式中：p（x）、p（y）分别表示图像中位于x＝（u，v）T和y＝（u′，v′）T处的像元灰度值，当这两个位置的像元灰度值满足式（9）中第1个条件时，τ的值为1，否则为0。

特征点邻域内的nd个（x，y）点对能够唯一地确定一组二进制τ检测，BRIEF描述符就是nd维的二进制向量，其表达式为

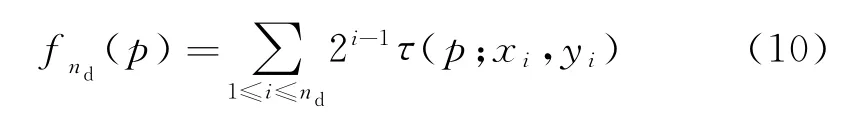
式中：nd可以为128、256或512，考虑到速度和鲁棒性，本文中nd＝256。在特征点的S×S邻域内选择nd个（xi，yi）像素点对，当xi、yi服从高斯分布（0，S2／25）时，采样的像素点对在各个方向性能一致。

为使特征点的BRIEF描述符具有旋转不变性，采用特征点圆形邻域的矩心确立的主方向θ，将nd个像素点对变换到主方向确定的坐标系下，得到像素点对旋转后的BRIEF描述符

式中：Rθ是主方向确定的二维旋转矩阵，即

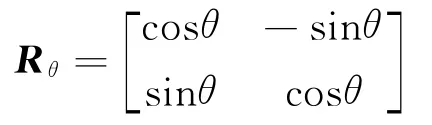
将旋转后的像素点对的BRIEF描述符Sθ，通过式（10）建立特征点的二进制向量描述符，使特征点具有旋转不变性。

2 同名点匹配

同名点匹配是在相邻两幅影像提取的特征点及其描述符建立的基础上，首先以最近邻匹配中的最近邻特征点距离与次近邻特征点距离的比值匹配同名点，然后采用RANSAC方法剔除误匹配的同名点，最后得到精确匹配的同名点。

2.1 最近邻匹配

同名点的匹配需在两幅重叠影像的特征点及描述符建立完成后，本文采用最近邻匹配方法匹配同名点［13］。ORB算法的二进制向量描述符选定为32维，由于空间维度较低，通过比较描述符之间欧式距离的大小评价相邻影像上特征点的相似程度，描述符之间的欧式距离表达式为

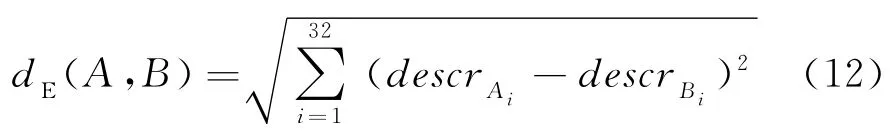
式中：A、B分别为相邻两幅影像的两个特征点；descrA和descrB分别为描述符；dE（A，B）是描述符的欧式距离。

寻找特征点与待匹配点的最近邻特征点距离N N（Nearest Neighbor）和次近邻特征点距离SCN（Second Nearest Neighbor），如果N N／SCN的比值小于给定的阈值，则认为这组特征点相互匹配。

根据FAST算法对特征点的定义，检测得到的特征点同样也只存在darker或者brighter两者之一的状态，重叠影像的同名点必然处于同一种状态，因此在计算欧氏距离之前先判断特征点的明暗状态，不同状态的特征点不用计算描述符的欧氏距离，从而可以节省匹配时间。

当特征点数量比较多时，在基准点集和目标点集之间采用穷举搜索方法寻找同名点是一个非常费时的过程。为了提高特征点的搜索速度，按照特征点描述符的维度对搜索空间进行划分，构建KD-树来加快特征点的检索，可以极大地缩减匹配过程。

2.2 误匹配剔除

由于影像获取环境的光照变化以及噪声等因素干扰，特征点的匹配不可避免的存在错误，为提高匹配的准确率，本文采用RANSAC方法剔除误匹配的同名点，具体步骤为：

Step1在齐次坐标系下，两张重叠影像上的一对同名点Xp＝（x，y，1）T和Xq＝（x′，y′，1）T满足透视变换关系

hi（i＝1，2，…，8），理论上至少4对同名点可以计算出两幅影像间的变换关系。

Step2随机地选取4组同名点，计算单应性矩阵H中的8个未知参数。

Step3计算剩余匹配点的相似性测度ρ，如果小于阈值ε，则选定为内点，并存入内点集S，否则被认为是外点。相似性测度为

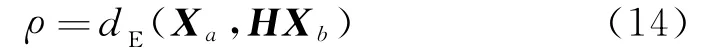
式中：Xa、Xb为一组候选同名点；dE为透视变换后匹配点坐标的欧式距离。

Step4统计内点集S中内点的数量，如果内点的个数大于4，则记录下所有的内点；否则返回到Step2。

Step5经过K次随机抽样后，选择内点数量最大的内点集S′作为最终的精确匹配结果，并用S′估计单应性矩阵H。其中采样次数K＝log（1－p）／log（1－w4），匹配点是内点的概率p应大于95%，内点占数据点集的比例w视具体情况而定。

3 实验与结果分析

3.1 实验数据

本实验的影像数据是利用Canon EOS 5D MarkⅡ数码相机结合车载近景摄影装置，在杭甬客运专线绍兴段采集的无砟轨道近景影像，见图2。相机传感器CMOS的尺寸为36 mm×24 mm，镜头焦距为24 mm，摄影平台高度为1.4 m，影像像素行列数为5 616×3 744，影像地面分辨率为0.4 mm。由图2可见，影像成像范围内主要是钢轨、轨道板及扣件等铁路构筑物，图像特征相对较少，影像色彩信息较为单一，图像灰度数值具有较高的相似性，尤其是钢轨的颜色基本保持在同一色调。

3.2 实验结果分析

为验证在铁路轨道近景影像纹理特征差异小且灰度变化不显著时，ORB算法进行特征点提取与匹配的可靠性和稳定性，本文同时采用ORB算法和SURF（Speeded up Robust Features）算法［15］进行铁路轨道近景影像特征点的提取与匹配，并对这两种算法的结果进行对比与分析。

图2 杭甬客运专线采集的无砟轨道近景影像

采用ORB算法对图2中的两幅影像进行匹配，具体参数设置情况见表1。两幅影像实际提取得到的特征点数量为2 040个，如图3（a），从图中可看出特征点的分布较均匀，没有聚簇现象，主要位于轨道板上，可为同名点匹配提供高质量的数据。在特征点匹配时，采用最近邻匹配得到粗匹配同名点个数是626对，经RANSAC方法提纯后得到同名点个数是266对，如图4（a）所示，图中用红色直线连接左、右两张影像上的同名点，同名点较为均匀地分布在轨道板上，可为铁路轨道近景影像的拼接提供高质量的数据基础。

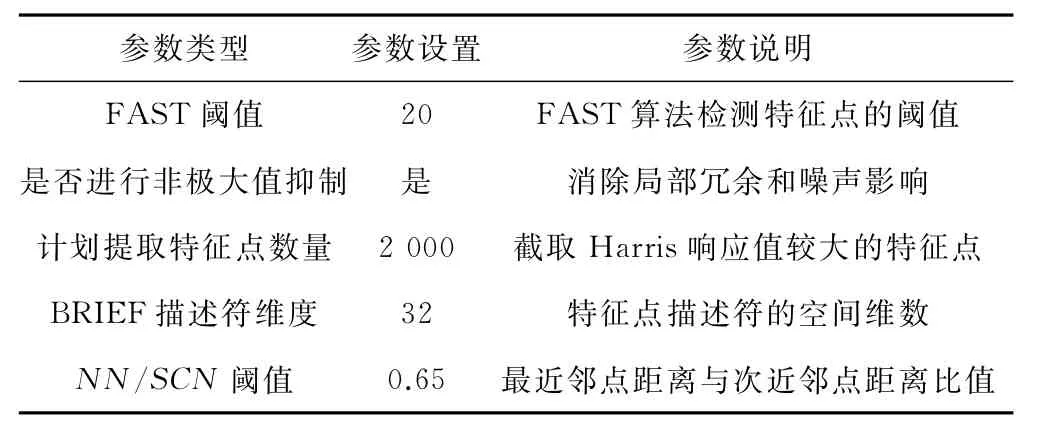
表1 ORB算法参数设置情况

图3 采用两种算法分别提取影像特征点

图4 采用两种算法匹配的同名点

采用SURF算法对图2中的影像进行特征点匹配，具体参数设置情况见表2。SURF算法提取得到的特征点如图3（b），在图3（b）中左影像特征点数量为5 148个，右影像特征点数量为3 998个，从图中可看出特征点分布不够均匀，存在聚簇现象，主要集中在轨道板边缘位置，这类点为边缘点，其稳定性相对较差，不利于特征点匹配。在特征点匹配时，粗匹配得到的同名点个数有630对，精匹配得到的同名点个数有214对，结果见图4（b），同名点分布较集中，主要位于轨道板边缘位置，会影响到轨道近景影像的拼接。

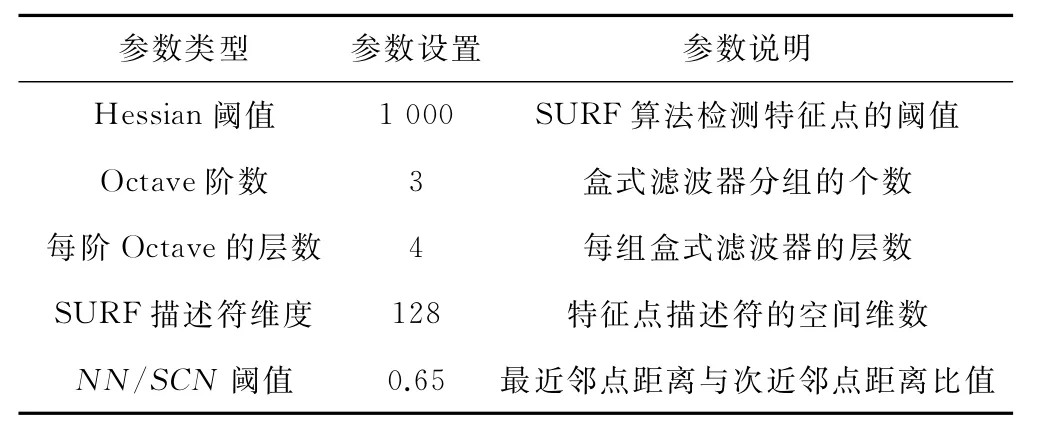
表2 SURF算法参数设置

分别以两种算法匹配得到的同名点为基础，将图2中的两幅影像进行拼接，结果见图5。

图5 轨道影像两种算法下拼接结果比较

从图5中可见，基于ORB算法的影像拼接效果较优，没有拼接缝隙，拼接质量较好；而基于SURF算法的影像拼接在上侧轨道有明显的错位，拼接缝隙较为明显，如图5（b）中圆圈所标记的地方，拼接质量较差。由此可见，基于ORB算法的轨道近景影像匹配得到的同名点稳健性相对更好。

ORB算法和SURF算法均在Visual Studio 2008 C＋＋平台上编写，所用计算机的CPU为2.67 GHz，系统环境内存为2 GB，整个影像匹配过程消耗的时间，见表3。

由表3可得出，基于ORB算法的铁路轨道近景影像特征点提取与匹配全过程消耗的时间约为SURF算法的1／16，即 ORB算法的时间效率明显优于SURF算法，可达到近实时处理的要求；尤其当铁路轨道近景影像数量巨大时，ORB算法较SURF算法其优势将更加突出。

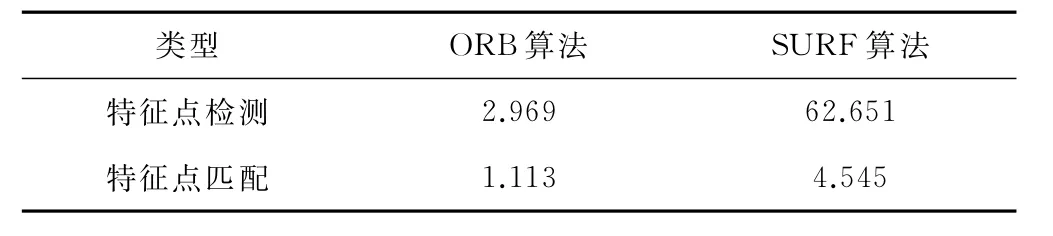
表3 ORB算法和SURF算法匹配时间对比 s

4 结束语

本文提出采用ORB算法对高速铁路轨道近景影像进行特征点提取，采用最近邻距离与次近邻距离的比值及RANSAC方法完成同名点匹配，以匹配的同名点为基础进行相邻影像的拼接。通过对杭甬客运专线上采集的无砟轨道影像进行处理，结果表明，在高速铁路轨道近景影像纹理特征差异小且灰度变化不显著的情况下，ORB算法能够提取到足够数量且分布均匀的同名点；利用这些同名点进行图像拼接，ORB算法较SURF算法得到了较好的拼接结果；在计算效率方面，ORB算法明显优于SURF算法。本文实验表明，采用ORB算法进行铁路轨道近景影像特征点自动识别与无缝拼接，可为近景摄影测量检测高速铁路轨道几何平顺性提供重要的图像技术支撑。

［1］熊卫东，周清跃，穆恩生.高速铁路钢轨的平顺性［J］.中国铁道科学，2000，21（3）：76-83.

XIONG Weidong，ZHOU Qingyue，MU Ensheng.The Smoothness of High-speed Railway Track Rails［J］.China Railway Science，2000，21（3）：76-83.

［2］蔡成标，翟婉明，王其昌.轨道几何平顺性安全限值的研究［J］.铁道学报，1995，17（4）：82-87.

CAI Chengbiao，ZHAI Wanming，WANG Qichang.Study on Allowable Safety Criterion of Track Geometric Irregularities［J］.Journal of the China Railway Society，1995，17（4）：82-87.

［3］陈强，刘丽瑶，杨莹辉，等.基于双向近景摄影测量检测轨道平顺度的计算模型［J］.铁道学报，2012，34（12）：83-89.

CHEN Qiang，LIU Liyao，YANG Yinghui，et al.Track Regularity Determination Model form Two-way Closerange Photogrammetry［J］.Journal of the China Railway Society，2012，34（12）：83-89.

［4］陈强，刘丽瑶，杨莹辉，等.高速铁路轨道几何状态的车载摄影快速检测方法与试验［J］.铁道学报，2014，36（3）：80-86.

CHEN Qiang，LIU Liyao，YANG Yinghui，et al.Static Geometry Measurement of High-speed Railway Tracks by Vehicle-borne Photogrammetry［J］.Journal of the China Railway Society，2014，36（3）：80-86.

［5］张祖勋，张剑清.数字摄影测量学［M］.武汉：武汉大学出版社，1997.

［6］RUBLEE E，RABAUD V，KONOLIGE K，et al.ORB：an Efficient Alternative to SIFT or SURF［C］／／Proceedings of IEEE International Conference on Computer Vision（ICCV2011）.New York：IEEE，2011：2564-2571.

［7］ROSTEN E，DRUMMOND T.Machine Learning for High-speed Corner Detection［C］／／Proceedings of the 2006 European Conference on Computer Vision（ECCV）.Berlin Heidelberg：Springer Verlag，2006：430-443.

［8］HARRIS C，STEPHENS M.A Combined Corner and Edge Detector［C］／／Proceedings of Alvey Vision Conference.Manchester：AVC，1988：15-50.

［9］ROSIN P L.Measuring Corner Properties［J］.Computer Vision and Image Understanding，1999，73（2）：291-307.［10］HU M K.Visual Pattern Recognition by Moment Invariants［J］.IRE Transactions on Information Theory，1962，8（2）：179-187.

［11］王耀明.图像的矩函数：原理、算法及应用［M］.上海：华东理工大学出版社，2002.

［12］CALONDER M，LEPETIT V，STRECHA C，et al.BRIEF：Binary Robust Independent Elementary Features［C］／／Proceedings of the 2010 European Conference on Computer Vision （ECCV）.Berlin Heidelberg：Springer Verlag，2010：778-792.

［13］SZELISKI R.Computer Vision：Algorithms and Applications［M］.London：Springer Verlag，2011.

［14］吴福朝.计算机视觉中的数学方法［M］.北京：科学出版社，2008.

［15］BAY H，TUYTELAARS T，VAN GOOL L.SURF：Speeded Up Robust Features［C］／／Proceedings of the 2006 European Conference on Computer Vision（ECCV）.Berlin Heidelberg：Springer Verlag，2006：404-417.