基于旋转变压器的牵引电机转速与转角测量技术研究

魏星原， 王立德， 申 萍， 岳 川， 白璐瑶

（北京交通大学 电气工程学院，北京 100044）

在常用的光电编码器、霍尔传感器和旋转变压器等位置传感器中，由于旋转变压器精度高、结构坚固、可靠耐用，其大量应用于机器人、机床、飞机、雷达、卫星天线等工业场合［1］。尤其在极端恶劣环境下，如极限高低温或者强振动等，旋转变压器将逐渐代替光电编码器［2］。因此，近些年列车牵引与制动系统领域逐步使用旋转变压器作为电机转速和转角传感器。但在列车中，由于受旋转变压器本身安装、制造工艺以及列车运行环境等影响，旋转变压器的输出存在误差，根据误差信号表现规律的不同，它们可以分为偏移误差、幅值误差、相位误差和谐波误差［3］。误差的存在会干扰电机转速和转角信息的测量结果，影响列车的安全运行，因此如何减小这些误差显得至关重要。

传统的减小误差方法包括硬件方法和软件方法。常见的硬件方法有通过改进硬件电路减少输出信号的非理想特征达到抑制误差的目的［4］，但硬件本身的精度和温漂特性影响该方法抑制误差的效果。软件方法包括误差修正表法和数值分析法等。

也有学者从误差的来源出发，提出其他一些算法减小误差。文献［5］在同步旋转坐标系锁相环法SRFPLL（Synchronous Rotating Reference Frame-based Phase Locked Loop）的基础上提出使用高级自适应谐振滤波器来降低误差对角度计算的影响。文献［6］提出高级自适应数字锁相环法AADPLL（Advanced A-daptive Digital Phase Locked Loop）消除随机噪声造成的误差。文献［7］采用改进加权最小二乘法实时计算误差参数然后进行消除。文献［8］提出一种双同步旋转坐标系锁相环法DSRF-PLL（Double Synchronous Reference Frame-based Phase Locked Loop），利用双旋转坐标系将不平衡的两相旋转变压器信号分解到正反向旋转的两个坐标系上，通过锁相环控制正向旋转矢量的q轴分量为零，使输出角度与正向旋转矢量一致，这种方法精度高且对误差信号有抑制功能，但缺点在于分解到双旋转坐标系上会增加响应时间，影响控制系统的实时性。

本文基于双广义二阶积分器法DSOGI（Dual Second Order Generalized Integrator）来提取不平衡旋转变压器信号的正序分量，然后利用TypeⅡ跟踪锁相环对获得的正序分量进行计算获得准确的速度和角度信息，设计一种减小误差的新型旋转变压器信号转换器，这种方法结构简单，响应时间短。最后通过仿真及实验对比测试了SRF-PLL、DSRF-PLL和DSOGI对含有相同误差的旋转变压器输出信号的解码性能，实验结果表明这种新型旋转变压器数字转换器能够实现自适应容错控制，大幅提升控制系统的转子转速和转角信息的获取精度，并具有暂态波动小和响应时间短的特性。

1 旋转变压器测角系统工作原理

旋转变压器是一种输出电压随转子转角变化的绝对位置传感器。具有分辨率高、输出阻抗低、工作温度范围宽等特点，近些年使用在列车牵引制动系统中充当转速信息和转角信息检测的传感器，参与控制系统的闭环控制。一对极旋转变压器结构见图1。S1－S2为正弦绕组，C1－C2为余弦绕组，R1－R2为激磁绕组，θ为转子转角。

图1 一对极旋转变压器示意图

转子绕组为激磁绕组，其上的激磁信号通过电刷或者定子的磁场耦合得到。两相定子绕组彼此正交放置易产生正弦信号和余弦信号，分别称为正弦绕组和余弦绕组［9］。

与光电编码器可以直接输出位置信号的脉冲量或数字量不同，旋转变压器的输出为包含角度信息的模拟信号量［10］，即

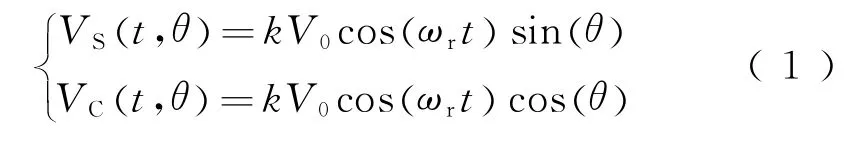
式中：VS（t，θ）为正弦绕组输出信号；VC（t，θ）为余弦绕组输出信号；k为转子绕组与定子绕组有效匝数比；V0为激磁信号幅值；ωr为激磁信号角频率。

该模拟信号需使用轴角数字转换器RDC（Resolver-to-Digital Converter）［11］进行解码才能得到转子的转速信息和转角信息。旋转变压器测角系统结构见图2。φ为测角系统计算角度。通常用于解调旋转变压器信号的方法是在激磁信号峰值处对正余弦信号进行采样。但由于信号传输的时延，在误差存在时，峰值采样会进一步放大误差信号，影响测角系统的精度。为减小干扰，获得高精度的角度信息，文献［8］提出采用一种基于相敏解调的高精度解调方法。

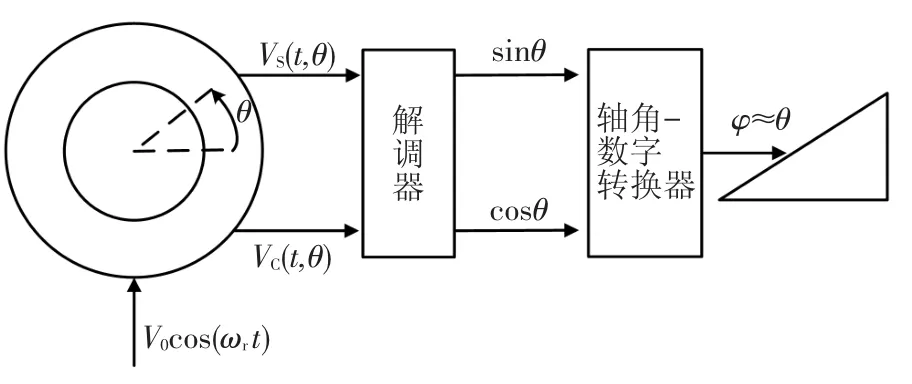
图2 旋转变压器测角系统示意图

理想状态下解调后的旋转变压器信号

式中：vC为解调之后的余弦信号；vS为解调之后的正弦信号；V1为解调之后的正余弦信号幅值。

理想旋转变压器信号是一组幅值相等的正交信号，但在非理想状态下，旋转变压器输出信号会出现误差，主要有以下4种：

（1）偏移误差：旋转变压器转子绕组输出信号中存在的直流成分。

（2）幅值误差：定子绕组与转子绕组的磁场耦合偏差或者轴角转换电路的增益不一样导致正余弦绕组的感应电势最大值不相等。

（3）相位误差：正弦绕组与余弦绕组的放置不完全正交以及在信号传输过程中存在电抗性元件导致两相信号产生相移。

（4）谐波误差：旋转变压器的气隙磁场不是绝对正弦分布而导致输出信号中含有某次谐波［12］。

4种误差中，转子绕组直流偏移误差经过激磁信号叠加后变为高频信号，通过低通滤波器消除，而谐波误差所占比例小于0.01%［13］，因此这两种误差信号影响较小。本文主要针对幅值误差和相位误差进行消除，假设含有这两种误差的旋转变压器信号一般形式

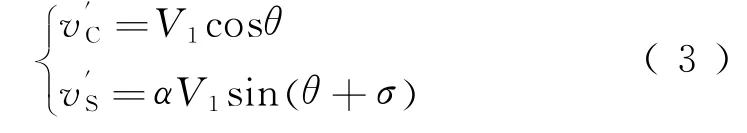
显然，直接利用这两相信号无法得到准确的转速和转角信息，但如果能分离提取得到幅值相同、相位正交的正序分量，就可以准确计算转速和转角信息。

2 具有误差抑制功能的解码算法研究

文献［8］提出一种基于DSRF-PLL的误差消除方案，利用两个反向的旋转坐标系：正向旋转的dq＋1坐标系和反向旋转的dq－1坐标系提取输入信号的正序和负序分量。这种方法精度高且对误差信号有一定消除作用，复杂的正反向解耦模块和其中所需的低通滤波器会增加锁相环处理时延，从而影响闭环系统的瞬态响应和稳态性，导致系统在低速状态很不稳定，暂态波动大、响应时间长，因此实际中很少使用DSRFPLL。

针对DSRF-PLL的缺点，本文提出一种新型误差抑制方案，使用双广义二阶积分器提取两相旋转变压器信号的正序分量，然后利用TypeⅡ跟踪锁相环对获得的正序分量进行计算得到准确的转速和转角信息。

在三相电网中，三相电压经过Clarke变换可以得到一组正交信号［14］

式中：

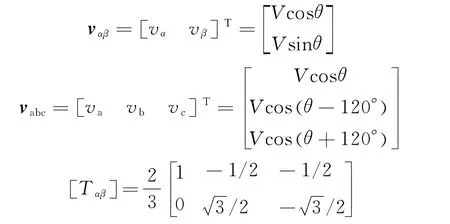
三相电压vabc进行Clarke变换得到两相电压vαβ；V为电压幅值。

对比式（2）和式（4）可以看出，解调后的旋转变压器输出信号可以类比为三相电压经过Clarke变换得到的一组正交信号。

vαβ的瞬间正序分量

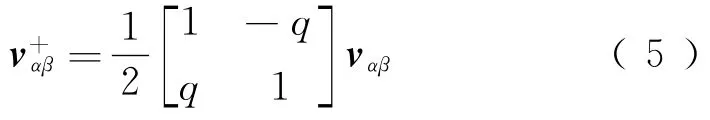
式中：q为正交变换算子，q＝e－j（π／2）。

广义二阶积分器作为一种新型电流谐波消除技术被应用于电力系统中，本文利用它来实现信号的正交变换［15］。广义二阶积分器原理见图3。v′和qv′为v经过广义二阶积分器生成的一组正交信号；K为广义二阶积分器控制参数；ω′为广义二阶积分器系统共振频率。

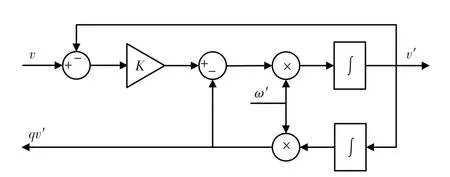
图3 广义二阶积分器示意图

其传递函数

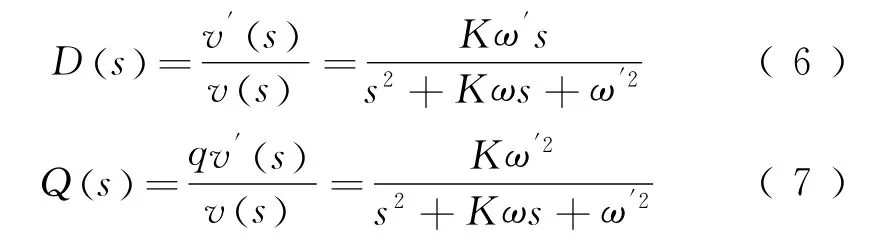
式中：ω为输入信号频率。

控制参数K变化时对应的传递函数波特图见图4。由波特图可以看出不论K、ω和ω′的值如何变化，广义二阶积分器输出信号总是一组正交信号v′和qv′，其中v′与输入信号v相位相同、幅值相等。比较发现K取值越小，广义二阶积分器对谐波和噪声抑制效果越明显，但同时响应时间越长。本文取K＝1.414，此时广义二阶积分器具有比较理想的响应时间与谐波抑制效果［16］。

确定广义二阶积分器的控制参数后，下一步基于它提取正序分量，见图5。为vα、vβ分别经过广义二阶积分器产生的正交信号为双广义二阶积分器提取的正序分量。

理想情况下，vα与vβ是一组幅值相等、相位相差90°的正交信号。当旋转变压器输出信号出现相位误差和幅值误差时，vα与vβ写为

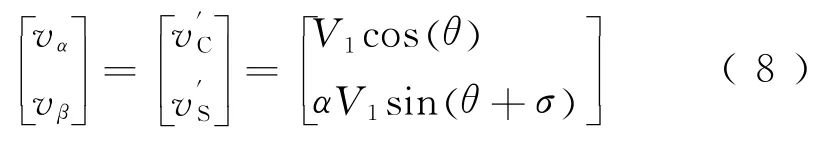
根据式（6）、式（7）求得

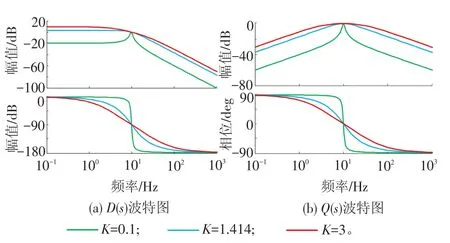
图 4 D(s)与 Q(s)波特图

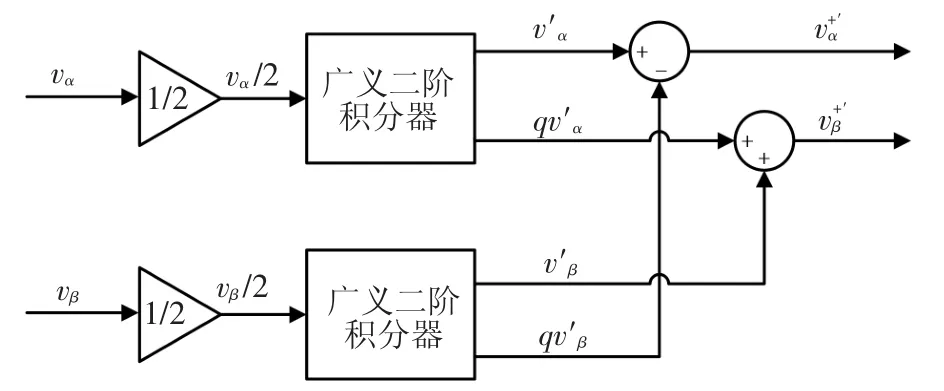
图5 利用广义二阶积分器提取vα与vβ正序分量示意图

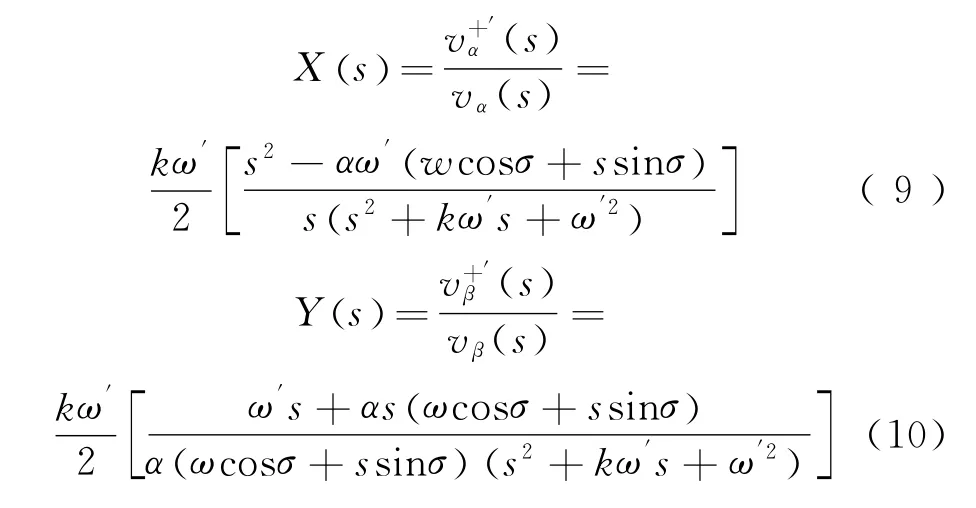
转换到Fourier频谱分析上

式中：

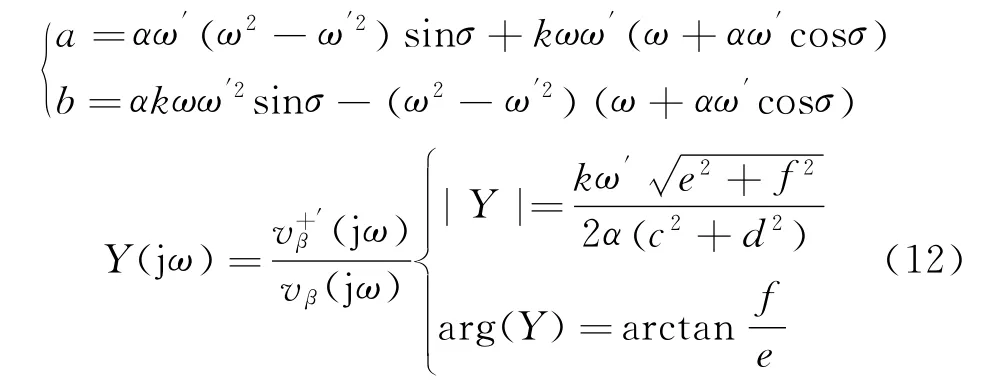
其中

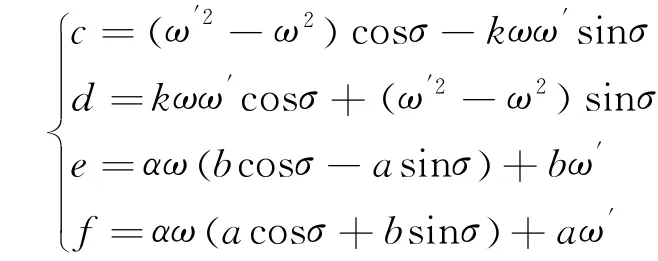
当ω′＝ω时，可以得到

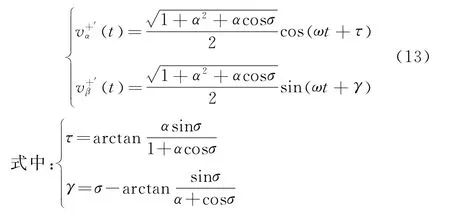
利用三角函数可以证明τ等于γ，因此，通过DSOGI得到两相幅值相同、相位正交的正序分量。然后利用TypeⅡ跟踪锁相环对获得的正序分量进行计算以获得准确的速度和转角信息［17］，见图6。sinθ、cosθ为输入信号，φ为计算轴角，ε为计算角度与真实角度θ的差值。

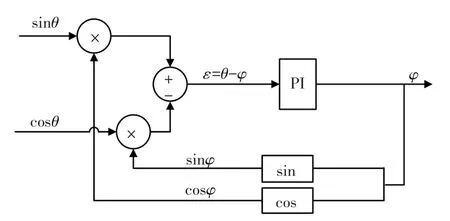
图6 TypeⅡ跟踪锁相环示意图

使用三角函数公式

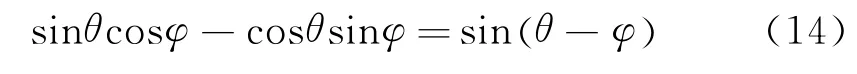
当θ－φ≈0时

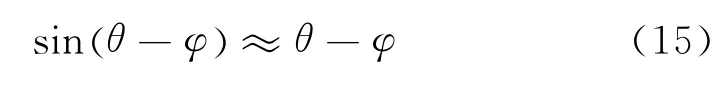
通过调节差值ε的大小使之趋近于0，即完成估算角度φ对真实角度θ的跟踪。

上述理论计算表明该新型旋转变压器解码方案能够自适应消除旋转变压器输出信号的误差，不论幅值误差与相位误差如何变化，DSOGI都可以分离提取旋转变压器不平衡两相输出信号的对称正序分量，再通过TypeⅡ跟踪锁相环计算得到准确地转速与转角信息，实现对误差的抑制，与DSRF-PLL相比结构更加简单，不需要复杂的解耦模块，减少计算量。

3 仿真研究

使用Matlab／Simulink搭建仿真平台，对DSOGI和DSRF-PLL两种算法在极端恶劣环境下的解码性能进行测试。仿真中幅值误差设置为60%，相位误差为30°，为了较直观地显示算法对误差的抑制效果，仿真中也测试常规旋转变压器解码算法SRF-PLL对误差的抑制性能，并将这三种方案的计算结果与实际转速和转角大小进行比较。仿真中，三种方案采用一致的参数以保证相同的瞬态响应，PI环节参数kp＝2.22，ki＝246.7，输入信号波形见图7。

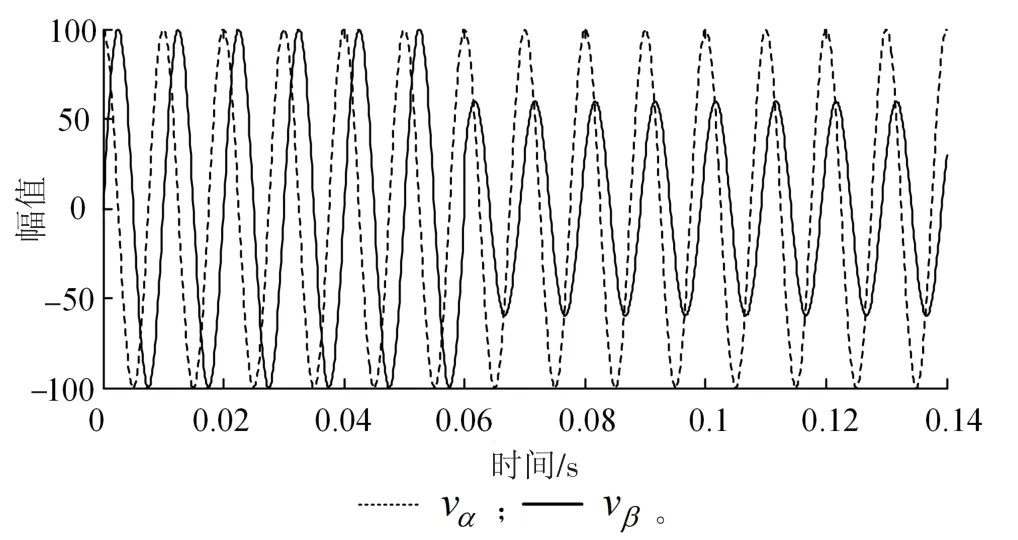
图7 输入信号在60ms产生误差

当t≤0.06 s，输入信号

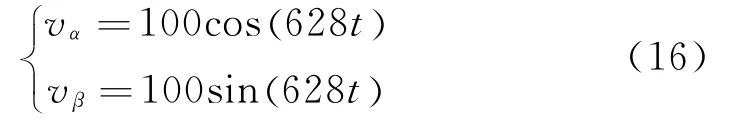
当t＞0.06 s，输入信号

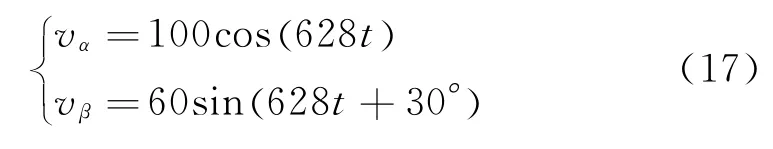
DSOGI和DSRF-PLL对输入信号正序分量的分离提取结果分别见图8（a）、8（b）。

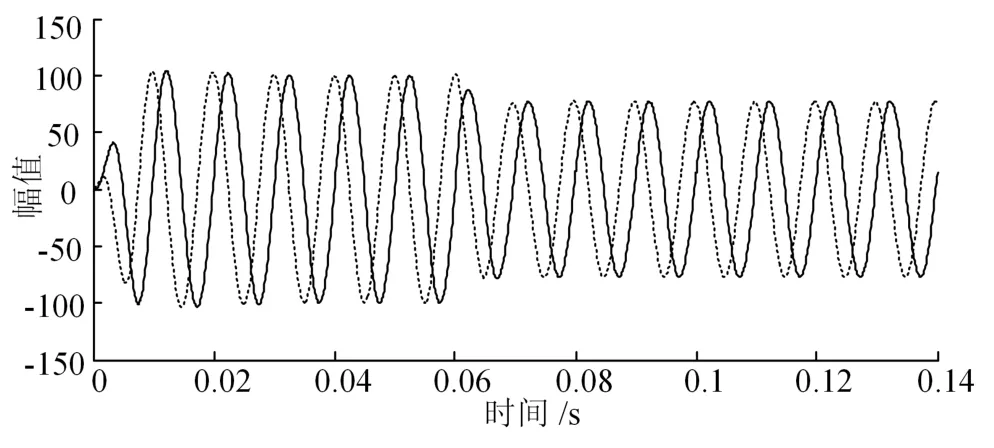
(a)DSOGI分离提取正负序分量

图8 DSOGI、DSRF-PLL分离提取正负序分量仿真结果

SRF、DSRF和DSOGI三种方案的计算转速和实际转速对比（图9（a））以及计算角度和实际角度对比（图9（b）、9（c））见图9。其中图9（b）为图9（a）在0.06 s至0.1 s的放大图，图9（d）为图9（c）在0.105 s至0.106 s的放大图。

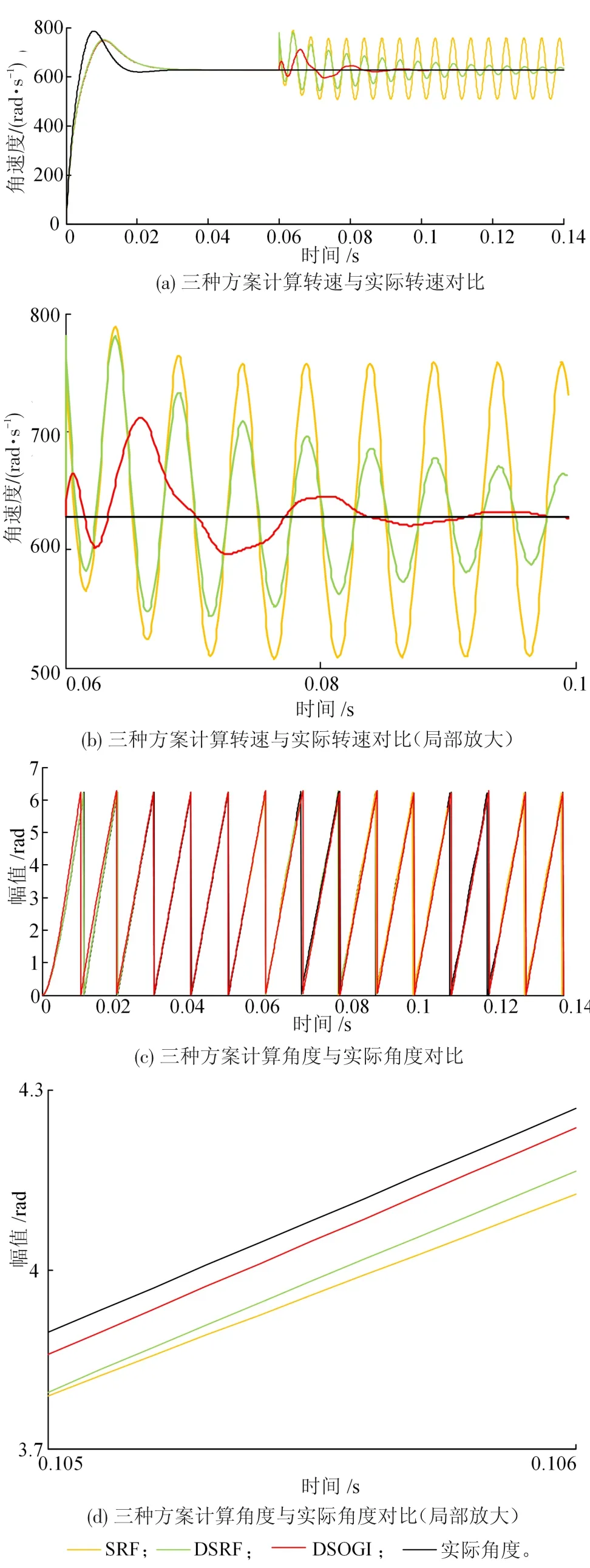
图9 三种方案转速、角度仿真波形

由仿真结果可以看出，在相同旋转变压器输出信号和参数设置条件下，DSOGI的计算结果和真实结果更接近，且暂态波动和响应时间都好于DSRF，验证了极端误差条件下DSOGI仍能准确提取出误差信号的正序分量，准确计算出转速信息和转角信息，对误差具有良好的消除效果，解决了DSRF-PLL计算复杂、响应时间长、暂态波动大的问题。

4 实验验证

最后利用TMS320F28335DSP进行实验验证，进一步评估这几种解码方案的性能。高性能DSP具备12位分辨率的ADC模块和32位浮点运算单元，广泛应用于电机、逆变器和数控机床的控制［18］。另外，使用美国国家仪器NI（National Instruments）公司的高性能PXI-6251 DAQ板卡在实验室环境下模拟旋转变压器输出。该板卡具有2路16位、2.00 MS／s模拟信号输出通道，可以通过Lab VIEW编程模拟得到极端条件下的误差信号，而使用真实的旋转变压器很难实现。实验中，输入信号参数设置和仿真一致，在0.06 s时产生误差，以便更好地测试几种方案的暂态波动和响应时间。SRF-PLL、DSRF-PLL和DSOGI三种方案计算的角度与实际角度对比见图10。从图中可以看出，DSOGI的稳态误差较小，在旋转变压器输出信号存在严重误差时仍能准确计算电机转速与转角。为进一步评估文章所提方案应用于牵引电机转速与转角测量的可行性，增加暂态响应实验以测试该方案在牵引电机速度变化时的暂态波动与响应时间。

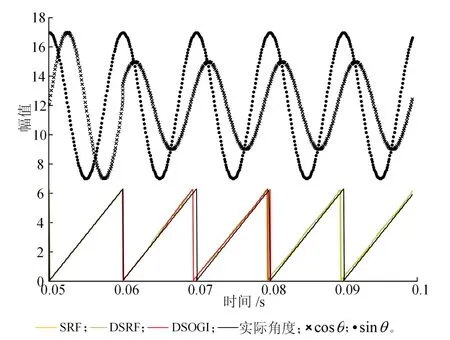
图10 稳态响应实验结果

实验中旋转变压器输出信号角速度在0.1 s时由314 rad／s阶跃到376.8 rad／s，并且在0.1 s时加入误差信号，其中幅值误差α＝0.6，相位误差σ＝30°。实验波形见图11，其中图11（a）为速度突变时SRF、DSRF和DSOGI三种方案的计算频率对比，图11（b）为速度突变时SRF、DSRF和DSOGI三种方案的计算角度与实际角度对比。

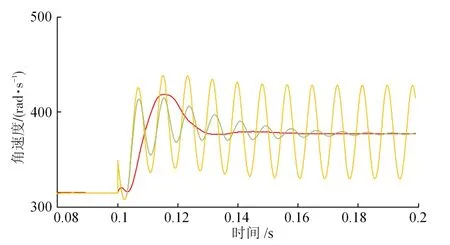
(a)速度突变时三种方案计算转速对比

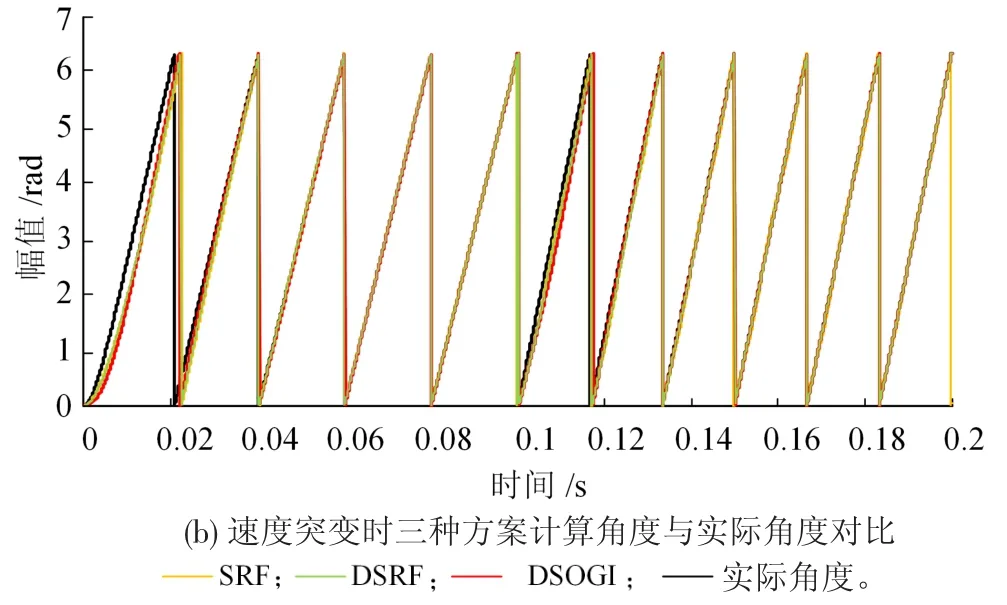
图11 暂态响应实验结果

稳态实验与暂态实验证明这种新型旋转变压器数字转换器能够自适应诊断出旋转变压器输出的误差并实现容错控制，与现有的SRF和DSRF解码技术相比，具有暂态波动小、响应时间短的优点，对恶劣环境下引起的旋转变压器输出误差具有良好的抑制效果，能够提升牵引电机转速和转角的测量精度。

5 结束语

本文提出一种基于旋转变压器的牵引电机转速与转角测量技术，针对极端恶劣环境下旋转变压器的输出误差较大导致测量不准确这一问题，引入对称分量法抑制旋转变压器输出误差，设计一种具备自适应抑制误差功能的新型全数字旋转变压器解码方案。

理论分析表明，这种基于双广义二阶积分正序分量提取的新型旋转变压器数字转换器能够自适应抑制旋转变压器输出信号的误差，相对于双同步旋转坐标系锁相环技术，本文提出的方案无需进行正反向解耦或瞬时对称分量分离，结构更加简单，减少了计算量。仿真研究与实验结果表明，该方法在极端恶劣环境下能够自适应抑制旋转变压器输出误差，准确地解码出电机转速与转角信息，具有良好的误差抑制性能。

［1］BENAMMAR M，GONZALES A S P.Position Measurement Using Sinusoidal Encoders and All-analog PLL Converter with Improved Dynamic Performance［J］.IEEE Transactions on Industrial Electronics，2016，63（4）：2414-2423.

［2］莫会成，闵琳.现代高性能永磁交流伺服系统综述——传感装置与技术篇［J］.电工技术学报，2015，30（6）：10-21.

MO Huicheng，MIN Lin.Summary of Modern High Performance Permanent Magnet AC Servo System：Sensor Device and Technology［J］.Transactions of China Electrotechnical Society，2015，30（6）：10-21.

［3］ZHANG J，WU Z.Automatic Calibration of Resolver Signals via State Observers［J］.Measurement Science＆Technology，2014，25（9）：2223-2237.

［4］MINGJI L，YU Y，JIBIN Z，et al.Error Analysis and Compensation of Multipole Resolvers［J］.Measurement Science＆ Technology，1999，10（12）：1292-1295.

［5］GONZALEZ-ESPIN F，FIGUERES E，GARCERA G.An Adaptive Synchronous-reference-frame Phase-locked Loop for Power Quality Improvement in a Polluted Utility Grid［J］.IEEE Transactions on Industrial Electronics，2012，59（6）：2718-2731.

［6］HOANG H V，JEON J W.An Efficient Approach to Correct the Signals and Generate High-resolution Quadrature Pulses for Magnetic Encoders［J］.IEEE Transactions on Industrial Electronics，2011，58（58）：3634-3646.

［7］HOSEINNEZHAD R，BAB-HADIASH AR A，HARDING P.Calibration of Resolver Sensors in Electromechanical Braking Systems：a Modified Recursive Weighted Leastsquares Approach［J］.IEEE Transactions on Industrial E-lectronics，2007，54（2）：1052-1060.

［8］BERGAS-JANE J，FERRATER-SIMON C，GROSS G，et al.High-accuracy All-digital Resolver-to-digital Conversion［J］.IEEE Transactions on Industrial Electronics，2012，59（1）：326-333.

［9］FIGUEIREDO J.Resolver Models for Manufacturing［J］.IEEE Transactions on Industrial Electronics，2011，58（8）：3693-3700.

［10］SARMA S，AGRAWAL V K，UDUPA S.Software-based Resolver-to-digital Conversion Using a DSP［J］.IEEE Transactions on Industrial Electronics，2008，55（1）：371-379.

［11］CARUSO M，TOMMASO A O D，GENDUSO F，et al.A DSP-based Resolver-to-digital Converter for High-performance Electrical Drive Applications［J］.IEEE Transactions on Industrial Electronics，2016，63（7）：4042-4051.

［12］BUNTE A，BEINEKE S.High-performance Speed Measurement by Suppression of Systematic Resolver and Encoder Errors［J］.IEEE Transactions on Industrial Electronics，2004，51（1）：49-53.

［13］HANSELMAN D C.Techniques for Improving Resolverto-digital Conversion Accuracy［J］.IEEE Transactions on Industrial Electronics，1992，38（6）：501-504.

［14］戴攀，刘田，周浩.高速铁路接触网行波传播特性研究［J］.铁道学报，2014，36（2）：25-30.

DAI Pan，LIU Tian，ZHOU Hao.Characteristics of Travelling Wave Propagation in Catenary of High-speed Railway［J］.Journal of the China Railway Society，2014，36（2）：25-30.

［15］YUAN X，MERK W，STEMMLER H，et al.Stationaryframe Generalized Integrators for Current Control of Active Power Filters with Zero Steady-state Error for Current Harmonics of Concern under Unbalanced and Distorted Operating Conditions［J］.IEEE Transactions on Industry Applications，2002，38（2）：523-532.

［16］RODRIGUEZ P，LUNA A，MUNOZ-AGUILAR R S，et al.A Stationary Reference Frame Grid Synchronization System for Three-phase Grid-connected Power Converters under Adverse Grid Conditions［J］.IEEE Transactions on Power Electronics，2011，27（1）：99-112.

［17］EMURA T，WANG L.A High-resolution Interpolator for Incremental Encoders Based on the Quadrature PLL Method［J］.IEEE Transactions on Industrial Electronics，2000，47（1）：84-90.

［18］李伟，马志文，蔡华斌，等.无二次滤波环节的单相四象限整流器输入电流控制研究［J］.铁道学报，2014，36（5）：28-32.

LI Wei，MA Zhiwen，CAI Huabin，et a1.Control of Input Current of PWM Rectifier without Secondary Filter Circuit［J］.Journal of the China Railway Society，2014，36（5）：28-32.