中国上市保险公司风险度量适用性研究

王向荣 周静宜

【摘 要】 风险度量是衡量公司经营状况的重要指标，如何全面有效地评估我国保险公司信用风险，降低信用风险发生的可能性和投资损失，最终实现风险的有效预测和管理，成为目前保险和投资业界的重要课题。为验证两种保险业信用风险度量方法的有效性，文章选取四家上市保验公司2015—2017年的财务数据，对Z模型和KMV模型在信用风险度量的适用性进行了比较研究，并利用非参数检验进行了实证分析。研究结果表明：Z模型与KMV模型都能在一定程度上识别风险，但在对保险公司信用风险的识别能力上，KMV模型在我国上市保险公司的适用性要优于Z值模型。因此，运用KMV模型能够更好地预测我国上市保险公司的信用风险。

【关键词】 保险业; Z模型; KMV模型; 信用风险

【中图分类号】 F842.0  【文献标识码】 A  【文章编号】 1004-5937（2018）23-0084-05

一、引言

随着保险业的发展，我国逐渐成为一个保险大国。但我国保险业务尚不发达，国民经济相关领域还未被保险业全面覆盖，业务深度尚待进一步挖掘，中国保险机构在国际领域的竞争力和影响力都远远不足，还不能算是保险强国，我国保险业面临重要的发展机遇和挑战。进一步拓展保险业务的深度和广度，增强核心竞争力，成为我国保险业和保险机构的重要发展方向。然而，保险业务经营的安全性、稳定性直接关系到人民群众的生活保障，也影响着国民经济的稳定与发展，如果保险公司经营不善，不仅会造成保险人经济上的损失，而且可能引发一系列深刻的社会问题与危机。当前，国内外经济发展中依然存在许多动荡因素，全球经济增长态势不明朗，增长趋势缓慢。我国經济也面临诸多困难，但实现新旧动能转换，提质增效“缓中趋稳、稳中向好”的前进趋势依然是经济发展的主旋律。在这过程中，保监会严格监督并积极推进行业转型升级，使得我国保险行业处在黄金发展机遇期。与此同时，金融风险定会为企业发展带来不利影响，而企业的发展与稳定又影响着经济的态势，信用风险作为金融风险的主要风险之一，直接影响着一个企业甚至一个行业的发展与稳定。因此，如何度量、弱化、监督和防御信用风险，如何有效降低风险发生的可能性及损失，如何确保我国保险行业高效运行，如何为我国营造一个良好的市场环境，如何实现转型升级，都是当前亟待解决的问题。

信用风险是金融风险中最常见的一种风险，普遍存在于各类交易市场中，狭义上是指另一方在债务到期时不履行义务的风险，具有不确定性、隐蔽性、传递性和难以有效管理等特点[ 1 ]。我国保险市场在国民经济的迅速增长中产生了非常大的需求空间，进而使得保险行业一直处在高速发展阶段，因此必然会涌现并累积大量的信用风险。据保险年鉴资料显示，我国部分未上市的保险公司因为偿付能力不能达到营业要求而被强制逐出市场，因此上市保险公司的信用风险度量与监管是当前整个保险行业经济发展中一个亟待解决的问题。信用风险的评估方法随着时代的发展产生了相继变动，传统的评估方法主要有专家法、信用评分法等。其中，专家法因其标准的不一致性和操作的困难性，目前已不被大多数保险公司采用。信用评分法首先需要找出影响违约概率大小的相关因素，其次赋予每个因素一个权重，最后经过加权得到一个总分，由于其使用方式简便、低成本的优点现阶段被广泛使用。主要的信用评分法包括多元判别模型、神经网络分析法和线性概率模型等。

目前，我国上市保险公司风险管理水平尚未达到一定标准，保险监管工作缺乏一定的主动性和预测性，大部分监管工作都是后期进行，监管能力有待进一步提升，而且还没有一个能够准确地预测风险、全面监控管理风险的模型。为了找到适合我国上市保险行业的风险度量模型，本文拟对信用风险度量应用最广泛的Z模型和KMV模型进行修正对比，选取我国四家上市保险公司进行实证分析，旨在选出最适合我国上市保险公司信用风险测评的模型来规避和预测风险，使我国保险市场能够平稳有序地发展，实现市场经济平稳转型。

二、Z模型

（一）Z模型基本思想

1968年，美国纽约大学教授爱德华·阿尔特曼在前人研究的基础上，提出了Z模型，引起了社会各界的巨大反响，大多数金融机构选择用它来预测信用风险，并取得了相关成果。当前，作为信用风险度量的主要模型之一，Z模型被外国企业广泛应用。该模型为多变量的分辨模型，需要计算出Z值，并对该值进行比较分析，计算时只需将相关财务指标填入[ 2 ]。

首先，选择保险公司中可以完全反映其财务情况以及偿债能力的财务比率;其次，依据保险行业的实际情况以及所查找的样本，确定每一比率的权重，将其与比率相乘再相加，即为Z;最后，对Z进行分析，得到可衡量保险公司信用风险的Z值。其中，Z值与企业信用风险呈负相关，即企业信用风险随Z值的增大而减小。根据我国的实际情况，普通的Z模型主要如下：

Z=1.2X1+1.4X2+3.3X3+0.6X4+1.0X5  （1）

其中：

X1=营运资产/总资产=（流动资产-流动负债）/总资产

X2=留存收益/总资产=（未分配利润+盈余公积）/总资产

X3=息税前利润/总资产=（税前利润+财务费用）/总资产

X4=权益市值/总债务账面值=（每股市价×流通股数+每股净资产×非流通股数）/总负债

X5=销售收入/总资产=主营业务收入/总资产[ 3 ]

因为普通的Z值模型适用于制造业，但是本文讨论的保险行业为非制造业，此行业没有销售收入，所以选取适用于非制造业没有X5变量的四变量模型，即：

Z=6.56X1+3.26X2+6.72X3+1.05X4  （2）

Z值模型有三种违约临界值，Z<1.23时，信用风险处于违约组;1.23<Z<2.9时，信用风险处于未知区;Z>2.9时，信用风险处于非违约组。

（二）Z模型实证分析

考虑数据的可得性及有效性，通过从证券之星、新浪财经以及公司年报选取所得样本数据。由于中国目前上市的保险公司有中国人寿、中国平安、中国太保和新华保险四家公司，因此选取这四家公司2015年、2016年和2017年三年的财务数据进行模型计算，其中股权市值的计算，选取每一年年末的收盘价作为每股市价[ 4 ]。

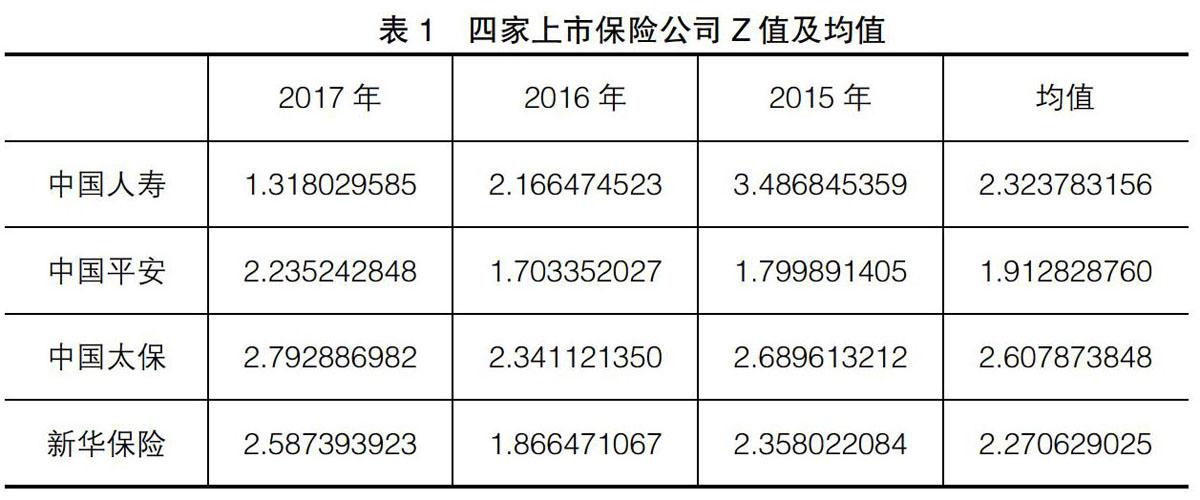
Z值计算结果见表1。

结合Z模型临界值，由表1可见，四大保险公司三年的Z值均值都处于信用风险未知区。当Z值越靠近2.9时，信用风险离非违约组的概率就会越大，相应的Z值越大信用风险就会越小，因此，由Z模型计算出信用风险最小的企业为中国太保，最大的为中国平安。

由于单个模型测算结果的准确度以及适用性难以判断，而我国四大保险公司信用风险是一个需要重点研究和预测的部分，因此为了确保结果的准确性以及该模型对保险行业的适用程度，引出KMV模型，测算结果是否一致，并进行模型对比，找出最适合我国上市保险公司信用风险度量的模型。

三、KMV模型

（一）KMV模型基本思想

在KMV模型中，公司资产价值等于负债价值的点为违约触发点，当公司资产价值低于违约触发点时，债权人和股东就会被公司违约。该模型主要基于资产的波动性来衡量当前市场价值低于违约触发点的可能性，假设资产包括股票和债券且资产价值的波动可以通过股票市价的波动性方差或标准差来表示[ 5 ]。KMV模型认为可以从企业预期资产价值的概率分布中计算出企业的预期违约概率（EDF），并获得预期违约损失。

（二）KMV模型内容

KMV模型的计算过程大体可以分为三步：首先，使用数据计算股票的市场价值及其波动性，利用期权价格模型求出公司的资产价值和波动性;其次，计算出违约距离（DD）用来表示违约风险;最后，计算公司的预期违约概率（EDF）。

详细计算步骤如下：

第一步，利用公式计算企业资产的市场价值及其波动率。通过期权定价理论，使用公司的股票价值、波动率以及负债账面价值来估算公司资产价值和波动性。计算时需假设资产收益的概率分布跟时间无关。计算公式如下：

E=VaN（d1）-De-rTN（d2）  （3）

其中，E为公司的股权价值，D为公司负债的市场价值，Va为公司资产的市场价值，r为无风险利率，T为债务期限，本文设为一年[ 6 ]。

σa为公司资产价值的波动率，只有Va和σa是未知量，因此需要求出这两个未知量，联立方程：

运用fsolve函数使用迭代方法计算方程组（3）、（4）、（5）、（6），求出公司资产的市场价值Va以及公司资产价值的波动率σa。

第二步，因为需要违约距离（DD）来比较信用风险的大小，违约距离与企业市场价值成正比，即随着违约距离的减小，企业市场价值会越接近违约点，将会有更大的可能性发生违约，因此会面临更高的信用风险。假设公司资产价值服从对数正态分布，那么可以通过KMV方程组计算出上市公司的违约距离。

其中，E（Va）为公司资产未来价值的期望值。DP为违约点，DP=SD+0.5×LD，SD为公司一年以下短期债务的价值，LD为未清偿长期债务的账面价值。

第三步，计算企业的预期违约概率EDF，EDF与DD呈反方向变动，相应的违约概率为EDF=N（-DD），N（-DD）为标准正态分布函数。

（三）数据说明

本文选取我国目前已经在上海证券交易所上市的四大保险公司，中国平安、中国人寿、中国太保、新华保险作为研究样本，计算基准日为2017年12月31日、2016年12月31日和2015年12月31日。樣本财务数据来源于新浪财经、证券之星以及四家上市保险公司3年的年报。

1.股权价值波动率的计算

要度量未来股票价格走势的不确定性，就要对四大保险公司的股权价值波动率进行估计。股票价格未来增减变化的可能性与其价格波动率呈正相关，即会随波动率的增大而增大。为使模型具有可比性，KMV模型的股权价值算法选择和Z模型一样的计算方法。

历史波动率法是以前一年上市公司的股价波动率为基础，估计未来一年的股权市场价值变化。本文选择此方法来估计四大保险公司股价变化。假设上市公司股票价格满足对数正态分布，则股票的对数收益率为：式中，Pi为股票收盘价格，Pi-1为股票前一日收盘价格，以此来计算收益率的波动率：

（8）式中，n为一年的交易天数，为收益率均值。因为我国证券市场周末和节假日休息，所以每年的交易天数为251天[ 7 ]，那么，上市公司股权市场价值的年波动率为：

2.无风险利率

本文用国有银行每年的定期存款利率作为无风险利率，其中，2017年和2016年为1.75%，2015年为2.25%。

3.时间范围T为一年。

（四）实证分析

联立公式（3）、（4）、（5）、（6）、（7），运用Matlab编写设计计算公式，计算出四家上市保险公司的股权价值、股权价值波动率、违约点、资产价值、资产价值波动率，2017年数据见表2。

由表2可见，2017年在股权市值与资产价值方面，四家上市保险公司资产价值与股权市值呈正相关，即股权市值越大，资产价值也越大。四家上市保险公司中，中国平安的股权市值最大，继而资产价值也占据首位，新华保险反之。

运用Matlab编写程序，计算出四家上市保险公司2017年的资产价值及资产价值波动率，其中中国平安的资产价值波动率位居第一。资产价值波动率越大，说明公司经营所面临的不确定性越大，相应风险不确定性也更大，因此中国平安的信用风险是四家公司中最难预测的。

由表2可见，2017年四家上市保险公司资产价值波动率由大到小依次为中国平安、新华保险、中国太保、中国人寿。因此，2017年中国平安相比其他三家保险公司，信用风险度量方面波动性更大。

为了比较公司之间信用风险程度，运用违约点DP代入公式（7），计算出四家上市保险公司三年违约距离及其均值见表3。

我国目前尚处在公司历史违约数据库不完善的阶段，还不能计算出精确的理论违约率。因此，本文将直接应用违约距离（DD）来比较我国已上市保险公司的相对违约风险大小[ 8-10 ]。

根据表3可知，四家上市公司三年的违约距离呈波动趋势，其中违约距离越小显示信用风险越大，由均值可知，四家公司中中国平安信用风险最大，中国人寿和中国太保均值相差甚微，显示信用风险较小。中国平安和新华保险的违约距离较小且基本接近，显示信用风险较大，两家公司皆以寿险业务为主，因此违约距离较小可能与两家公司寿险业务范围较广、保费收入地区分布处于劣势、高利率保单较多等因素有关。四家上市保险公司按信用风险大小降序排列为：中国平安、新华保险、中国太保、中国人寿，这与使用Z模型计算出的结果基本相近，因此，需要对两个模型进行对比研究，选出一个最适用的模型。

四、模型可比性分析

综上所述，我国四家上市保险公司中，运用Z模型计算出信用风险最大的公司为中国平安，最小的为中国太保，而利用KMV模型则计算出中国平安信用风险最大，中国人寿最小。模型之间计算结果基本相近，因此选取描述性统计分析和非参数检验对两个模型进行对比，选出最适用于我国上市保险公司信用风险度量的模型。

（一）描述性统计分析

描述性统计分析，即对所研究样本的数据进行统计性表述，通过统计方法将一组数据的集中性和波动性大小用简洁明了的数值体现出来。利用SPSS软件对两个模型进行描述性统计分析，计算四家上市保险公司三年的Z值均值和代表KMV模型的DD值均值的极大极小值、平均值和标准差。将Z值均值、DD值均值分别进行描述性统计分析，得到表4。

由表4可以看出，Z值模型和KMV模型计算出的均值、标准差之间具有较大的差异。Z值模型计算出的标准差远小于KMV模型。标准差小代表该组数据中大多数数值与该组数据的平均值之间差别很小，即离散程度较小，间接可以说明数据之间区分度较小;反之标准差较大，数据之间存在显著差异，区分度较大。因此，从描述性统计分析的结果中可以看出，标准差较小的Z值模型对我国上市保险公司的识别能力没有KMV模型高，因此其度量信用风险的能力没有KMV模型好。

（二）非参数检验

非参数检验与参数检验是统计推断的基本内容，也是统计分析方法的重要组成部分。当数据总体分布已知时，可使用参数检验对其参数的均值或方差等进行推断。但本文在分析数据时，无法预知总体的分布形态，因此参数检验在本文研究中不适用。所以，选取非参数检验，在总体方差未知的情况下，利用选中样本对总体分布形态进行推断。

非参数检验具有多种方法，本文数据总体为连续型随机变量，因此选择拟合优度的K-S检验方法，此检验通过样本数据的变化情况确定该样本的总体变化规律，从而判断其是否服从某一理论分布。

由表5可以看出，显著性水平DD值低于Z值，也就是说KMV模型的显著性水平低于Z模型。即KMV模型犯第一类错误的概率较小，犯错误概率较小即代表该模型精确度较高。因此，KMV模型精确度高于Z模型。

五、结论与建议

为了对保险公司风险度量的适用性进行研究，本文选取了我国全部四家上市保险公司进行对比和实证分析，运用描述性统计和非参数检验等方法对Z模型以及KMV模型进行模型检验和对比，证明在预测度量风险方面，KMV模型相比Z值模型更加准确，也表明在我国上市保险公司中Z模型与KMV模型都能在一定程度上帮助识别风险，但在准确性及有效性上存在差异，表现为KMV模型在我国上市保险公司的适用性要高于Z值模型，在对信用风险的识别能力上，KMV模型明显优于Z模型。利用非参数检验进一步证实了KMV模型在风险度量的精确度要高于Z模型，KMV模型具有更好地预测我国上市保险公司信用风险的能力，KMV模型不仅可以对现在的数据进行风险度量，而且可以预测未来的风险走向。原因可能在于Z模型是一个对于过去历史数据进行判定的模型，不能对未来以及动态的数据进行评判。Z模型仅仅利用若干特定的财务指标，但是其他的财务指标不一定不会对企业信用风险造成一定的影响，因此在某种程度上，该模型存在一定的局限性，这是一个弊端。

针对本文的结论研究，KMV模型在我国上市保险公司的适用性要高于Z值模型，但KMV模型在计算过程中也存在一定的缺陷，例如忽略了债券价值的波动对资产价值的影响。对于违约点的计算方法现阶段我国还没有一个统一的规定，对于违约概率的数据不能较好地运用等。对此，为了更好地帮助识别我国保险公司的信用风险，综合考虑两种模型，上市保险公司在进行风险度量时，应综合考虑保险公司风险的度量问题，多方面多角度度量企业的信用风险。

【参考文献】

[1] 冯楠楠.企业财务危机预警模型设立及分析[J].会计之友，2018（9）：113-115.

[2] 运迪，周建辉.基于改进Z值模型的企业信用风险评估与检验[J].统计与决策，2014（10）：73-176.

[3] 迟晨.基于Z评分模型对我国上市公司信用风险评估[J].商业文化，2011（2）：91-92.

[4] 于申珅.基于Z值模型的商業银行信用风险研究[J].企业研究，2014（14）：6-7.

[5] 王慧，张国君.KMV模型在我国上市房地产企业信用风险度量中的应用[J].经济问题，2018（3）：36-40.

[6] 周沅帆.基于KMV模型对我国上市保险公司的信用风险度量[J].保险研究，2009（3）：77-81.

[7] 闫丽瑞.基于KMV模型的信用风险度量研究[J].山西财经大学学报，2009（5）：104-108.

[8] 潘睿.我国上市企业基于KMV模型的实证研究[J].烟台大学学报，2017（4）：108-115.

[9] 曾诗鸿，王芳.基于KMV模型的制造业上市公司信用风险评价研究[J].预测，2013，32（2）：60-63，69.

[10] 姚德权，张宏亮，黄学军.基于变结构KMV模型的商业银行风险承担度量研究[J].中国软科学，2015（11）：109-122.