γ-α相变中不同晶界特征下铁素体生长形貌的相场模拟∗

张军 陈文雄 郑成武 李殿中

1)(中国科学技术大学化学与材料科学学院,合肥 230026)

2)(中国科学院金属研究所,沈阳材料科学国家(联合)实验室,沈阳 110016)

1 引 言

多晶材料中晶界特征会影响材料的力学行为,如韧脆性[1]等.而在微观组织演化过程中,晶粒的取向性生长也往往与晶界特征密切相关.晶界特征是指由于不同结构的晶体中原子按照特定的对称性排列,晶粒间界面上物理性质出现的差别[2].在固态相变过程中,新相的生长过程有别于一般的晶粒长大过程,化学驱动力和晶界能是控制新相生长过程的主要因素[2].若化学驱动力远大于晶界能,晶粒的取向生长较为不明显;但如果化学驱动力较小,晶粒的生长对晶界的各向异性就显得较为敏感.多相多晶粒系统中晶粒间的晶界特征(包括晶界能和晶界迁移率)的影响更复杂,不仅相与相之间存在不同类型的晶界,而且晶粒与晶粒之间也存在不同的取向关系,故形核于不同奥氏体晶界处铁素体晶粒的生长形貌容易出现多样性.近年来,为了描述晶粒的长大过程,研究者开发出许多模型[3−5]来研究晶粒的形貌演变和生长动力学.然而,这些模型大多仅考虑了晶界各向同性或有限条件下的各向异性的影响,与实际晶界特征相比存在较大差别.在这些模型中介绍的方法众多,相比较而言,相场法在真实和定量模拟上具有一些独特的优势[6−9].

相场法是一种通过系列场变量描述多晶组织的微观结构和成分的介观尺度研究方法,相场模型以相场变量在相邻结构或晶粒之间的离散范围来隐式地表达界面的宽度.如此,晶界能在模型中则表现为界面宽度范围内局部界面能密度的集合.近年来,相场法模拟单相多晶系统中晶粒生长取得了明显的进展.Kazaryan等[10]利用相场法研究了各向异性的晶界能和晶界迁移率对晶粒尺寸及取向差分布的影响,发现其有别于各向同性系统中的晶粒生长动力学和微观组织特征.Chang和Moelans[11]采用相场法研究了不同程度的晶界各向异性对高织构化组织演化的影响,探讨了界面多交叉点存在的稳定性.Miyoshi和Takaki[12]通过在多相场模型[13]中添加序参量的高阶耦合项,避免了三叉晶界处界面能不同带来的计算不稳定性问题,模拟了晶粒异常长大现象.

相场模拟的关键之处在于能把材料真实物性参数以唯象参数的形式有效地表达在模型中,这也是相场发展领域的研究热点[14]之一.但是,这些唯象参数的表达并不是简单的解析解[15].为准确地表达整个系统中不同的晶界特征,需要利用系列模型参数,包括能量梯度系数与耦合项系数等,同时考虑协调变化,否则容易导致计算过程中界面处相场变量的离散范围(即相场界面宽度)出现混乱.在薄界面近似的相场模型中,相场界面宽度会影响模拟的计算精度[16,17],故模拟过程中有必要保持相场界面宽度固定以保证计算精度.

本文采用多相场模型模拟奥氏体-铁素体相变过程中铁素体晶粒的生长行为.相场模型通过协调界面处模型参数定量表达晶界的各向异性特征,研究不同晶界特征下铁素体晶粒的形貌特征和生长动力学.最后,实现多相多晶粒组织相变的模拟,并与实际组织比较,分析不同奥氏体晶界处铁素体晶粒形貌的形成原因.

2 相场模型

2.1 相场方程

在多相多晶粒系统中,采用非保守场变量η(r,t)和保守场变量x(r,t)分别描述不同晶粒的取向与溶质浓度.选择两组序参量η1i(r,t)和η2i(r,t)分别表示奥氏体相和铁素体相的不同晶粒,其中η的第一个下标“1”和“2”分别表示奥氏体相和铁素体相,第二个下标i则表示晶粒取向,n为取向数,r与t分别表示空间位置与时间.

体系内系统总自由能F为[16,18]

式中,Fs和Fc分别为界面自由能和化学自由能,均为序参量η和溶质浓度x的函数.在多相多晶粒系统中,界面自由能Fs的计算引入了各向异性的影响,化学自由能Fc则通过计算各相的化学自由能与势阱函数的耦合而得到.

式中,fs为界面自由能密度,fc为化学自由能密度,V为系统体积.fs由序参量η构建,在晶粒内部值为0,而界面区域不为0,可表述为[15,16]

式中,f0为局部界面自由能密度,可表达为序参量的四阶多项式:

对于任意序参量,f0在晶粒内部取最小值0.在多晶体系中,能量梯度系数κ、耦合项系数ε和参数m受到各向异性晶界能的影响,具体论述见2.2节.

化学自由能密度fc为η与x的函数[18,19]:

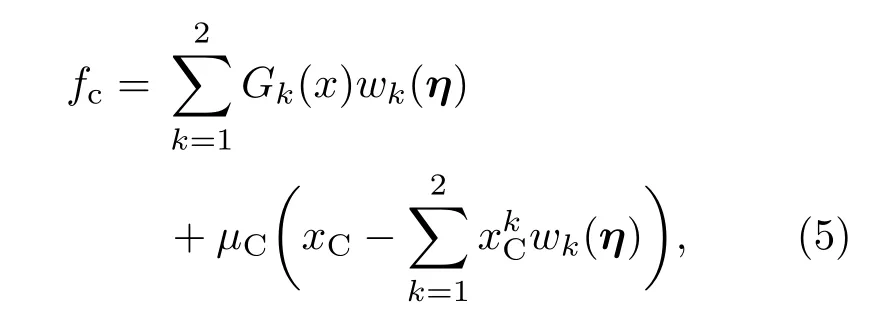
式中,wk(η)为势阱函数[18],其物理意义为相k在某处的体积分数;xC为某处的C浓度;xkC和Gk分别为k相的C浓度和化学自由能(相k为奥氏体相γ或铁素体相α).考虑C原子的长程扩散过程,界面处C浓度可表示为两相的混合[18]:

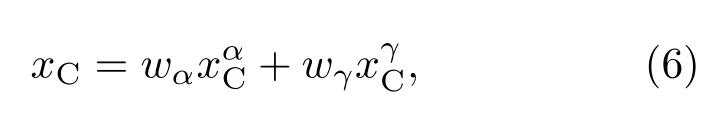
µC为C的扩散化学势,模拟中假设在相界面范围内奥氏体相的C扩散势与铁素体相的C扩散势相等[18]:

奥氏体相与铁素体相化学自由能Gk可采用规则溶体双亚点阵模型[20−22]计算.

C浓度场变量xC(r,t)的演化采用保守场的Cahn-Hilliard动力学方程[16]描述:式中,参数Mk为Mγ或Mα,它们分别为相场模型中奥氏体相和铁素体相中C原子的扩散迁移率,其与两相中C原子的物理扩散迁移率MγC和MαC有关,可参考文献[18].

序参量ηki(r,t)的演化采用非保守场的Allen-Cahn动力学方程[16]描述:

式中,L为与界面迁移率相关的模型参数,与各向异性界面迁移率M相关.

2.2 界面模型参数

相场法模拟铁素体晶粒生长的过程中,为了准确描述界面各向异性对相变过程的影响,需要在相场模型中确定界面处模型参数的物理意义,并对其进行定量表达.

从唯象理论上看,平直界面处界面能σ的计算可描述为[15]

(10)式可直接从(3)和(4)式得到,式中y表示坐标,而能量梯度系数κ、耦合项系数ε和参数m均与各向异性的界面能相关.通过变分原理和系列变量变换[15],(10)式可转化为

式中,场变量ηi与ηj(ηi)的分布及离散范围受能量梯度系数κ和耦合项系数ε的影响,局部界面自由能密度f0的分布也受κ和ε的影响.通常能量梯度系数κ和耦合项系数ε越大,局部界面自由能密度f0越大[15].但对于序参量的离散范围(即实际计算得到的相场界面宽度δ),κ和ε的作用不同:κ越大,序参量的离散范围越大;而ε越大,序参量的离散范围则越小.直接求解(11)式中序参量ηi的积分并不容易,但可以推导出,并且,(11)式中的积分部分也仅与耦合项系数ε相关,故(11)式可简化为

式中,g(ε)为耦合项系数ε的函数.当然,(12)式未考虑对序参量离散范围的约束,模拟计算过程中相场界面宽度δ可能会发生变化,从而影响模拟结果的准确性.为避免此问题,模型中利用模型参数对相场界面宽度进行约束[15]:

式中,(dηi/dy)y=0表示y=0处(相界面中心位置)的序参量梯度,此处序参量相交,存在ηi=ηj=ηinterf,f0取得最大值f0,interf,ηinterf值的大小与耦合项系数ε的大小成反比.结合(12)式和(13)式,可得到界面能和相场界面宽度与能量梯度系数和耦合项系数的关系.模型参数κ和m可表达为

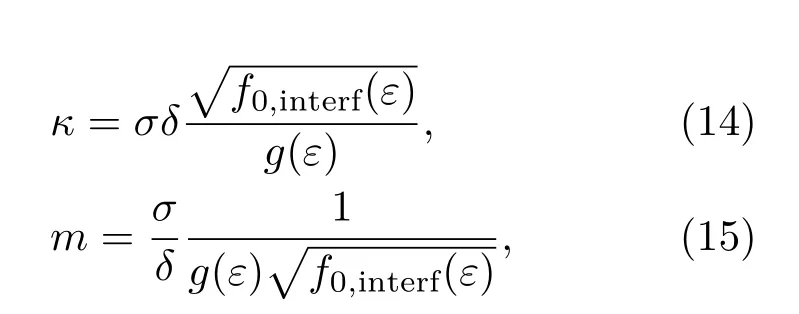
耦合项系数ε隐式地包涵在(14)和(15)式中,而g(ε)和f0,interf(ε)则可通过离散序参量(ηi,ηj)进行求解,可参考文献[15],其结果如图1所示.对此结果进行多项式拟合,即可得到关于ε的函数关系式和反函数g∗(ε)−1,将用于模型参数的求解过程中.(14)和(15)式体现了模型参数κ和m对相场界面宽度δ的约束.对于多晶体系,采用普适计算公式求解模型参数并不合适,需要根据不同晶界特征进行协调.此外,固定相场界面宽度δ有利于求解过程中数值计算的稳定性和准确性.

图1 (网刊彩色)g和f0,interf与耦合项系数ε的关系Fig.1.(color online)Values of the parameters g and f0,interfas functions of ε.

针对不同的晶界特征,结合(14)和(15)式,采用迭代方法求解(9)式中的模型参数κ,ε,L和m,过程如下[15].

1)初始化过程

(a1)参数初始化:各向异性界面能σ和界面迁移率M,设置相场界面宽度δ,初始化界面能σinit,初始化耦合项系数εinit,参数σinit和εinit可以设置为各向同性的界面参数,如εinit=1.5.

(a2)利用图1中拟合的多项式由εinit求解g∗(εinit)和f0∗,interf(εinit),计算

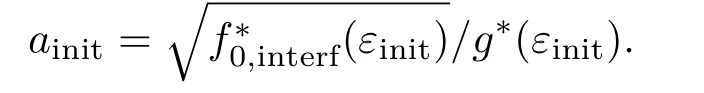
(a3)计算

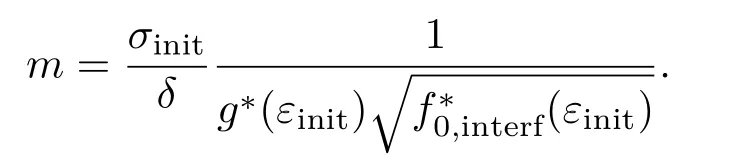
2)循环迭代过程

迭代参数:κ1,ε1,a1和ainit,待求解模型参数κ,ε和L.

(b1)计算κ1=σδainit.

(b2)计算g(ε1)=

(b3)利用图1中拟合的多项式由g∗(ε1)−1求解ε1,再由ε1求解f0∗,interf(ε1),计算

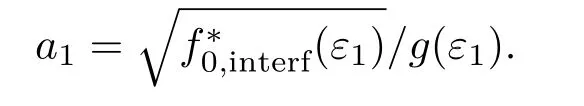
(b4)如果a1/=ainit⇒ainit=a1,返回步骤(b1);

否则,得出κ=κ1,ε=ε1,a=a1,L=M/(δainit),计算终止.

本文主要讨论晶界能与晶界迁移率的各向异性对奥氏体-铁素体相变的影响,其大小受不同晶界取向的影响.相对于一个参考取向角,每个晶粒存在一个取向角θi(θi=[0,π]),并假定其在相变过程中不发生变化.各向异性晶界能σi,j可通过晶粒间的取向差Δθi,j=θi−θj来计算[23]:

式中,σi,j为i/j相之间相界面的最大晶界能,如σα,γ等.本文假设晶粒间晶界取向差Δθi,j＜Δθm时,该界面为小角度晶界;当Δθi,j≥Δθm时,该界面为大角度晶界;Δθm在此取15°.

图2 (网刊彩色)晶界能σ和晶界迁移率M与取向差Δθ之间的关系Fig.2.(color online)Scaled grain boundary energy σ and mobility M as functions of the misorientation Δθ.

晶界迁移率与取向差之间的关系可用如下近似模型[23−25]来确定:

式中,Mi,j为i/j相之间相界面的最大迁移率,如Mα,γ等.图2为不同取向差Δθ下的晶界能与晶界迁移率.在小角度晶界下,随着取向差Δθ的增加,晶界能与晶界迁移率均增大.

2.3 模拟条件

本文以Fe-0.1C-0.5Mn(wt.%)合金为原型材料模拟1123 K等温过程中发生的奥氏体-铁素体相变.模拟所用的物性参数[26]列于表1.

表1 模拟所采用的物性参数[26]Table 1.The physical parameters used in simulations.

整个模拟区域离散成规则正方形网格.计算时间步长Δt与空间步长Δy间满足关系Δt＜Δy2/(4Mα,γ).边界条件设置为周期性边界条件,采用有限差分和迭代方法对动力学方程(8)和(9)进行求解.为避免网格形状带来的误差和满足计算精度的要求,预设相场界面宽度δ与Δy的关系为[16]:δ=nΔy(4≤n≤ 6),Δy=0.4µm.模拟中固定相场界面宽度δ=6Δy,并利用2.2节中介绍的迭代方法计算出不同晶界能的能量梯度系数κ和耦合项系数ε,结果如图3所示.可以发现κ和ε都随着晶界能的增加而增大,意味着界面处的序参量分布会发生变化,如图4所示.

图3 (网刊彩色)能量梯度系数κ和耦合项系数ε与晶界能σ之间的关系Fig.3.(color online)The model parameters κ and ε as functions of the interfacialenergy σ.

图4(a)和图4(b)分别为铁素体晶粒α在奥氏体晶粒γ1和γ2之间生长的相场值和序参量沿图中虚线的分布. 模拟设置晶界能σα,γ1＜σα,γ2. 从图4(a)和图4(b)中可以看出,不同晶粒间界面处的相场值和序参量的大小及变化范围均收敛较好,图4(a)中α/γ2界面处的最低相场值(序参量相等时,即ηinterf=ηα=ηγ)要小于α/γ1界面处的最低相场值,此结果也能从图4(b)中α/γ1和α/γ2界面处ηinterf值大小得出,这表明晶界能在模型中得到了正确的反映.此外,图4(b)显示α/γ1和α/γ2界面宽度保持不变,界面处序参量的离散范围保持一致,表明该模型能有效控制计算精度.引入不同晶界能时,虽然会改变界面处序参量大小的分布,但不会改变相场界面宽度而引起误差.

图4 (网刊彩色)(a)铁素体生长过程中相场值的分布情况;(b)序参量沿图4(a)中虚线的分布情况Fig.4.(color online)(a)Distribution of the phasefield values during ferrite growth;(b)pro file of the order parameter along the dashed line in Fig.4(a).

3 结果分析与讨论

3.1 原始奥氏体晶界能对铁素体生长的影响

已报道的相场模型大多仅考虑了奥氏体相与铁素体相之间的晶界能σα,γ在相变过程中的影响,而对奥氏体与奥氏体相之间晶界能σγ,γ的影响则少有关注,但事实上,σγ,γ也是影响相变过程的一个重要因素.为讨论原始奥氏体晶界能对相变的影响,模拟中保持σα,γ不变,设置不同的σγ,γ值进行模拟,考察铁素体晶粒形貌和转变动力学.随着σγ,γ取值的变化,相场模型中奥氏体与奥氏体界面处的能量梯度系数κ和耦合项系数ε随之改变. 从图3的结果可以看出,σγ,γ/σα,γ∈[1.0,2.0]时,κ∈[0.9×10−7,1.8×10−7]且ε∈[1.5,10].σγ,γ/σα,γ增大,κ和ε也将增大, 界面处自由能密度fs升高,会加快界面处相场变量的演化.

图5 (网刊彩色)(a)铁素体晶粒α与奥氏体晶粒γ1和γ2之间的相界面轮廓示意图,β为三叉界面平衡角;(b)—(e)不同σγ,γ/σα,γ值对α/γ 相界面轮廓的影响:(b) σγ,γ/σα,γ =1.0;(c) σγ,γ/σα,γ =1.25;(d) σγ,γ/σα,γ =1.5;(e) σγ,γ/σα,γ =2.0Fig.5.(color online)(a)Schematic of the interface pro file between the ferrite α and austenite γ1and γ2;(b)–(e)the simulated α/γ interface pro files under different σγ,γ/σα,γ ratios:(b) σγ,γ/σα,γ =1.0,(c) σγ,γ/σα,γ =1.25,(d) σγ,γ/σα,γ =1.5,(e)σγ,γ/σα,γ =2.0.The equilibrium angle β is determined from the intersection of the grain boundaries.

图6 不同σγ,γ/σα,γ值下相界面平衡角β的变化情况Fig.6.The equilibrium angles β at the triple junction under different σγ,γ/σα,γ ratios.

图5为不同σγ,γ/σα,γ比值下的α/γ相界面轮廓的模拟结果.模拟中设置单一铁素体晶粒α在两个奥氏体晶粒γ1和γ2间生长,设置α/γ1界面能为σα,γ1,α/γ2界面能为σα,γ2, 并假定此处σα,γ1=σα,γ2=σα,γ,σγ,γ/σα,γ值分别取为1,1.25,1.5和2. 从图5可以发现, 不同σγ,γ/σα,γ值下三叉晶处平衡角β不同. 图6为β值随σγ,γ/σα,γ值的变化情况,图中不同σγ,γ/σα,γ值下β值的大小经过多次统计而确定,存在误差.从图6中可以发现, 当σγ,γ/σα,γ值从1逐渐增加到2时,β值从115°逐渐减小到80°.这表明晶界能的变化将导致三叉界面处平衡角β发生改变,从而影响铁素体晶粒的生长形貌. 需要说明的是,当σγ,γ/σα,γ=1时,β值小于120°,这是因为铁素体晶粒的生长是由化学驱动力和晶界能共同控制,三叉晶界处平衡角会偏离120°.

图7 (网刊彩色)不同σγ,γ/σα,γ 值下铁素体晶粒生长距离llength的演化情况Fig.7.(color online)Variation of the ferrite thickness llengthwith time under different σγ,γ/σα,γ ratios.

从图5中还可以看出,铁素体晶粒沿原始奥氏体晶界方向与垂直于奥氏体晶界方向的生长距离不同.由于σα,γ不变,晶粒α垂直于奥氏体晶界方向的生长距离lwidth基本相同,而沿原奥氏体晶界生长的距离llength则随σγ,γ/σα,γ值的增大而增加.图7给出了晶粒α初期生长过程中llength的演化情况.可以发现,对单一曲线,llength与时间t成线性关系,即铁素体沿原奥氏体晶界生长的速率基本不发生变化. 但各曲线的斜率不一样,σγ,γ/σα,γ值越大,曲线斜率越大,铁素体晶粒的生长速率越快.清晰地认识不同类型晶界对铁素体生长动力学的影响,将有助于分析不同晶粒形貌的形成原因.上述结果表明晶界能的提高会加快相界面迁移,改变相界面轮廓,从而影响铁素体晶粒的生长形貌.

3.2 α/γ晶界取向差对铁素体生长的影响

新相形核于母相之间的晶界上,会与紧邻的母相存在着不同取向关系,产生不同大小的晶界能和晶界迁移率,导致铁素体晶粒向不同奥氏体晶粒内的生长速率不同.模拟中设定晶界能比值σγ,γ/σα,γ为2, 为方便对比, 将α相晶粒与γ2母相晶粒之间的界面设置为大角度晶界(Δθα/γ2≥ 15°), 而与γ1母相晶粒之间的界面设置为不同取向差的小角度晶界(Δθα/γ1≤ 15°),进而模拟不同Δθα/γ1值对α晶粒生长形貌的影响.图8为t=40 s时不同取向差Δθα/γ1下铁素体晶粒形貌的模拟结果.可以看出,当α/γ1与α/γ2的取向差相等且其界面均为大角度晶界时,铁素体晶粒向奥氏体晶粒γ1和γ2内部生长的距离lwidth相同,铁素体晶粒呈椭圆形状(图8(a1));而当α/γ1的界面为小角度晶界时,铁素体晶粒向γ1内部的生长明显被抑制,而且取向角差Δθα/γ1越小,其生长距离lwidth越小.这是因为取向差Δθα/γ1值减小,晶界能随之变小,界面处的自由能密度fs降低,延缓了界面处相场变量的演化.图9统计了不同Δθα/γ1值下铁素体晶粒向奥氏体晶粒γ1内部生长的距离lwidth随时间的演化情况.可以看出,当Δθα/γ1较大时,相界面的迁移速率较快,α晶粒向母相γ1内部生长明显.取向差对相变过程的影响主要表现在对晶界能和晶界迁移率的影响上,如图2所示.因此,如果新形成的铁素体晶粒的取向与母相奥氏体晶粒取向相近,即使能提供足够高的化学驱动力,铁素体晶粒生长也会被抑制,如图8(a4)所示.故考虑晶界各向异性时,新相晶粒的生长存在多样性,在某些方向上正常生长,而在某些方向上缓慢生长,晶粒的局部生长形貌受到晶粒间取向的影响.晶粒间取向越接近,相对生长越缓慢.

图8 (网刊彩色)t=40 s时不同取向差Δθα/γ1下铁素体晶粒的生长形貌 (a1)Δθα/γ1=15°;(a2)Δθα/γ1=10°;(a3) Δθα/γ1=5°;(a4) Δθα/γ1=1°Fig.8.(color online)The simulated morphology of ferrite α at t=40 s with different misorientations Δθα/γ1:(a1) Δθα/γ1=15°;(a2) Δθα/γ1=10°;(a3) Δθα/γ1=5°;(a4) Δθα/γ1=1°.

图9 (网刊彩色)不同取向差Δθα/γ1下铁素体晶粒生长距离lwidth(α/γ1)的演化情况Fig.9.(color online)Evolution of the ferrite thickness lwidth(α/γ1)with different misorientations Δθα/γ1.

3.3 三叉晶界处铁素体晶粒的生长特征

为了更清楚地描述晶粒取向对铁素体晶粒生长形貌的影响,对三叉晶界处铁素体晶粒的生长形貌进行了模拟,如图10所示.考虑了三叉晶界处铁素体晶粒与3个奥氏体晶粒间之间的3种不同的取向关系:

1)铁素体晶粒与相邻2个奥氏体晶粒保持取向近似(取向非常接近,θα/γ≤ 1°),这种情况下铁素体晶粒仅向保持大取向差的奥氏体晶粒内部生长,向另外两个奥氏体晶粒的生长被抑制,如图10(a)所示.

图10 三叉晶界处铁素体晶粒的生长情况 (a) Δθα/γ1= Δθα/γ2 ≤ 1°,Δθα/γ3＞ 15°;(b) Δθα/γ1 ≤1°,Δθα/γ2= Δθα/γ3＞ 15°;(c) Δθα/γ1= Δθα/γ2= Δθα/γ3＞ 15°Fig.10.Evolution of the ferrite morphology at the triple junctions with different grain-boundary structures:(a) Δθα/γ1= Δθα/γ2 ≤ 1°,Δθα/γ3＞ 15°;(b) Δθα/γ1 ≤ 1°,Δθα/γ2= Δθα/γ3＞ 15°;(c) Δθα/γ1=Δθα/γ2= Δθα/γ3＞ 15°.

2)铁素体晶粒与其中1个奥氏体晶粒保持取向近似,此时铁素体晶粒向此晶粒内的生长被抑制,如图10(b)所示.

3)铁素体晶粒不与任何晶粒存在近似取向,此时铁素体进行等轴生长,如图10(c)所示.

3.4 与实验结果的对比

为实现与真实组织的比较,应用此模型模拟多相多晶粒系统中不同奥氏体晶界处铁素体晶粒的生长形貌. 模拟过程假设σγ,γ/σα,γ=2不变,并随机设置新形成的铁素体相晶粒与近邻奥氏体相晶粒之间的取向差.图11(a)为模拟得到的微观组织形貌,图中白色区域为新形成的铁素体相,灰色区域代表原奥氏体相,黑色表示相场界面.从图中可以看出不同奥氏体晶界处的铁素体晶粒形貌表现出明显差异.作为对比,图11(b)给出了Fe-0.1C-0.5 Mn(wt.%)合金在1123 K等温后淬火的金相组织,白色晶粒为铁素体相,其他区域为马氏体相(即高温时的奥氏体相).对比图11(a)与图11(b)可以发现,模拟的铁素体晶粒形貌能很好地反映实验中所观察到的现象.实验组织中观察到不同奥氏体晶界处铁素体晶粒展现出几种不同形貌,在模拟中也能找到相应的晶粒形貌.

1)形核于原奥氏体晶界:类型A和B.

2)形核于原奥氏体三叉晶界:类型C,D和E.

A类:铁素体晶粒仅向紧邻某个奥氏体晶粒内生长.

B类:铁素体晶粒向紧邻奥氏体晶粒内生长.

图11 (网刊彩色)模拟结果(a)与金相组织(b)的比较Fig.11.(color online)Comparison of the microstructure between the simulation(a)and the micrograph(b)in the given Fe-C-Mn alloy.

C类:铁素体晶粒仅向紧邻某个奥氏体晶粒内生长.

D类:铁素体晶粒向紧邻某两个奥氏体晶粒内生长.

E类:铁素体晶粒向紧邻奥氏体晶粒内生长.

以上不同类型的晶粒形貌反映出铁素体晶粒生长受到不同晶界特征的作用.模拟组织能很好地再现实际组织中铁素体晶粒生长形貌的多样性,表明了该模型的有效性和正确性.更重要的是该相场模型在物理和数学方面对界面模型参数进行了精细化处理,把物性参数准确地表达在相场模型中,故相场模拟结果具有明确的物理基础,并成功地反映到模拟结果中,能描述铁素体相变真实组织的特征.

4 结 论

1)所建立的多相场模型通过协调能量梯度系数和耦合项系数定量表达晶粒的晶界特征,且能固定相场界面宽度以保证必要的计算精度.本文相场模型可用于描述各向异性晶界作用下的相变行为.

2)相场模拟结果显示,晶界类型的变化会影响相变中三叉界面处的平衡角与新相晶粒的生长速率.晶粒间取向差会影响铁素体向紧邻奥氏体内的生长速率,晶粒间取向越接近,新相的生长越缓慢.

3)通过与实验结果对比,本文相场模型可成功描述奥氏体-铁素体相变过程中铁素体晶粒生长形貌的多样性,从而为相变过程中的复杂晶粒生长行为提供机理解释.

[1]Palumbo G,Lehockey E M,Lin P 1998JOM5040

[2]Xu Z,Zhao L C 2004Principle of Solid-State Transformation in Metal(1st Ed.)(Beijing:Science Press)pp7–19(in Chinese)[徐洲,赵连城 2004金属固态相变原理 (北京:科学出版社)第7—19页]

[3]Anderson M P,Srolovitz D J,Grest G S,Sahni P S 1984Acta Metall.32783

[4]Raabe D1998Mater.Sci.Forum.273–275169

[5]Fan D,Chen L Q 1997Acta Mater.45611

[6]Militzer M 2011Curr.Opin.Solid State Mater.Sci.15106

[7]Chen L Q 2002Annu.Rev.Mater.Res.32113

[8]McFadden G B,Wheeler A A,Braun R J,Coriell S R 1993Phy.Rev.E482016

[9]Steinbach I 2009Modell.Simul.Mater.Sci.Eng.17073001

[10]Kazaryan A,Wang Y,Dregia S A,Patton B R 2002Acta Mater.502491

[11]Chang K,Moelans N 2014Acta Mater.64443

[12]Miyoshi E,Takaki T 2016Comput.Mater.Sci.11244

[13]Steinbach I,Pezzolla F 1999Physica D134385

[14]Moelans N,Wendler F,Nestler B 2009Comput.Mater.Sci.46479

[15]Moelans N,Blanpain B,Wollants P 2008Phys.Rev.B78024113

[16]Moelans N 2011Acta Mater.591077

[17]Zhang X G,Zong Y P,Wang M T,Wu Y 2011Acta Phys.Sin.60068201(in Chinese)[张宪刚,宗亚平,王明涛,吴艳2011物理学报60068201]

[18]Zhang J,Zheng C W,Li D Z 2016Acta Metall.Sin.521449(in Chinese)[张军,郑成武,李殿中 2016金属学报521449]

[19]Eiken J,Böttger B,Steinbach I 2006Phys.Rev.E73066122

[20]Gustafson P 1987Metall.Trans.A18175

[21]Huang W 1990Metall.Trans.A212115

[22]Loginova I,Ågren J,Amberg G 2004Acta Mater.524055

[23]Holm E A,Hassold G N,Miodownik M A 2001Acta Mater.492981

[24]Takaki T,Tomita Y 2010Int.J.Mech.Sci.52320

[25]Kim Y J,Hwang S K,Kim M H,Kwun S I,Chae S W 2005Mater.Sci.Eng.A408110

[26]Zheng C W,Raabe D 2013Acta Mater.615504