基于相干光时域反射型的光纤分布式声增敏传感研究∗

陈文杰 江俊峰 刘琨 王双 马喆 张晚琛 刘铁根

(天津大学精密仪器与光电子工程学院,天津大学水利工程仿真与安全国家重点实验室,光电信息技术科学教育部重点实验室,天津大学光纤传感研究所,天津市光纤传感工程中心,天津 300072)

1 引 言

与电磁和压电传声器相比,光纤声传感技术具有抗电磁干扰能力强、对潮湿高温的恶劣环境适应力强、信号传输损耗小等优点[1−4].研究人员已提出多种光纤声传感方法,包括光纤光栅型[5,6]、光纤Fabry-Perot型[7]、马赫-曾德尔干涉仪型或迈克耳孙干涉仪型[8]、相干光时域反射型(C-OTDR)[9,10]、相位敏感光时域反射型(phase-OTDR)等[11].其中,基于C-OTDR或phase-OTDR的分布式光纤声传感技术具有传感规模优势.目前国内外研究人员初步展示了分布式光纤声传感系统的声探测能力,如Lu等[12]将传感光纤绕环固定于金属薄板上,基于C-OTDR分布式声传感系统探测到薄板附近的铅笔芯断裂发出的声信号;Wu等[13]将光纤直线粘贴于金属薄板上对空气中的声信号进行探测,能探测到最弱声压级72 dB;Shang等[14]采用调制相位载波解调算法提高解调信号的动态范围和灵敏度,将光纤绕环放置于水中进行声信号探测,探测最小声压为6 Pa,对应声压级135 dB.声传播是介质中压强的传播,光纤分布式声传感本质上是探测光纤中声导致的动态微应变[15].由于声信号是微小的压强,而光纤非常纤细且刚度大,声压直接在光纤上引起的应变非常小,导致灵敏度低.因此不少光纤分布式声传感研究采用压电陶瓷换能器(PZT)模拟声传感实验,如Wang等[16]基于phase-OTDR并采用3×3耦合器解调信号相位,使用2个PZT模拟声振动,展示多点声信号探测;Iida等[17]在phase-OTDR系统中采用多频系列脉冲研究以提高系统可探测信号频率,但实验中也使用PZT模拟声探测过程,未对实际声音信号进行探测.为实现高灵敏度的声传感,本文提出了一种基于单端开口波纹薄筒的光纤分布式声传感增敏方法,利用波纹薄筒的筒壁变形,将声压转化为光纤轴向应变.实验结果表明,该方法具有良好增敏效果,最小声探测信号声压级可至60.1 dB.

2 光纤分布式声增敏传感原理

2.1 基于C-OTDR的光纤分布式声增敏传感系统

基于C-OTDR的光纤分布式声增敏传感原理如图1所示,窄线宽激光器输出连续激光,经过50:50偏振分束器后,一半作为本地参考光,表示为

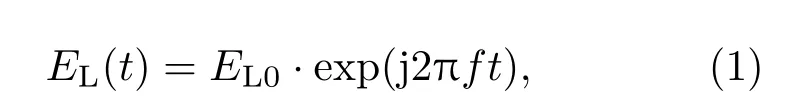
其中f为激光频率,EL0为本地参考光的电场振幅.另一半通过声光调制器(AOM)、掺铒光纤放大器(EDFA)被调制成移频脉冲光,再经过环形器,注入传感光纤中.移频脉冲光沿光纤传输,并在每处产生后向瑞利散射光,

其中,Es0(t)为返回瑞利散射光场振幅,随着衰减不同,返回信号光强是随时间变化的;Δf为经过AOM产生移频;φ(t)则为信号光与本地参考光相位差,表征沿光纤各处的应变情况.在90°光混合器,信号光与本地参考光相干产生四路干涉信号,在X偏振方向和Y偏振方向各有2个正交信号,

其中AX(t),AY(t)表示t时刻接收到X,Y偏振方向信号强度振幅,经过正交相位解调,即可得到相位差φ(t).由于时间t是光脉冲在光纤中往返运动的时间,对于位于光纤长度Z处的传感光纤,携带其传感相位信息的信号光返回的时间t为t=2nZ/c,其中n为光脉冲在光纤中的有效折射率,c为真空中光速.所以,在T时刻发出的脉冲测量得到的传感光纤位置所对应的相位差为ΦT(Z)=φ(t)=φ(2nZ/c),由于有重复的光脉冲周期性测量,得到传感光纤对应的一系列等时间间隔测量的该传感位置的相位差ΦT(Z),Φ2T(Z),Φ3T(Z),···,ΦnT(Z). 通过跟踪该位置的相位差变化,即可得到传感光纤周围的声信号.

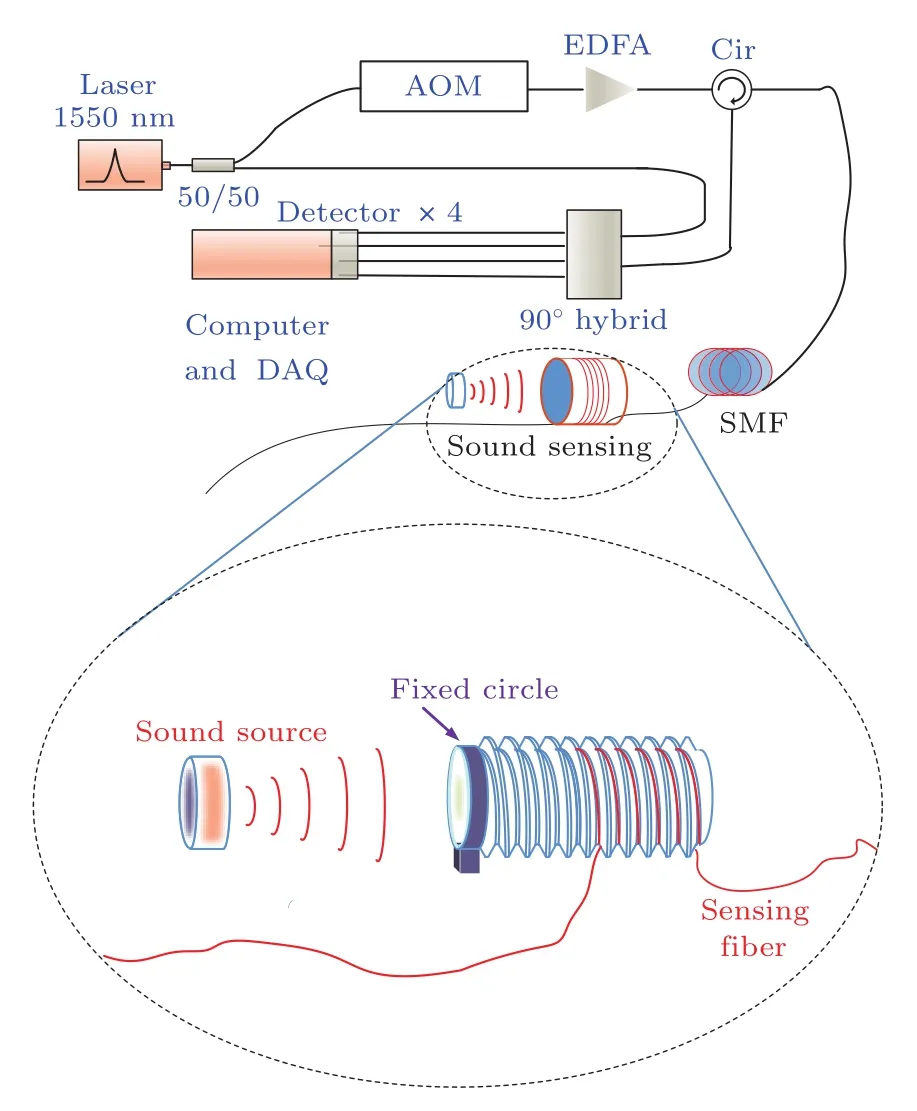
图1 基于C-OTDR的光纤分布式声增敏传感原理图Fig.1.Enhanced optical fiber distributed acoustic detection system based on C-OTDR.

2.2 单端固定开口波纹薄筒增敏模型

采用图2所示的单端固定开口波纹薄筒,进行光纤声传感局部增敏.光纤缠绕并粘贴于单端开口的单层波纹薄筒的波谷中,即传感光纤的轴向应变量等于所在波谷位置的环向应变量ε.对于单层波纹薄筒,其整体轴向刚度K可表示为K=K0/N,其中N为有效波节数,K0为单波节轴向刚度.

图2 基于波纹薄筒的光纤声传感增敏原理图Fig.2.Principle of fiber acoustic detection enhancement based on corrugated tube.

声信号通过开口进入波纹薄筒内部,激发波纹薄筒轴向受迫振动,带动缠绕于波纹薄筒波谷中的传感光纤发生形变,从而增强幅值响应.推动波纹薄筒底部沿轴向振动的最大位移ΔX与声信号的声压p和薄筒底面积S的乘积成正比,同时与整体轴向刚度K成反比,即有

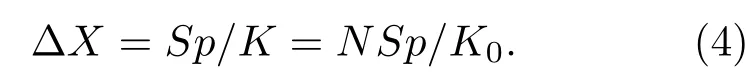
轴向拉伸或压缩产生的传感光纤应变ε大小为

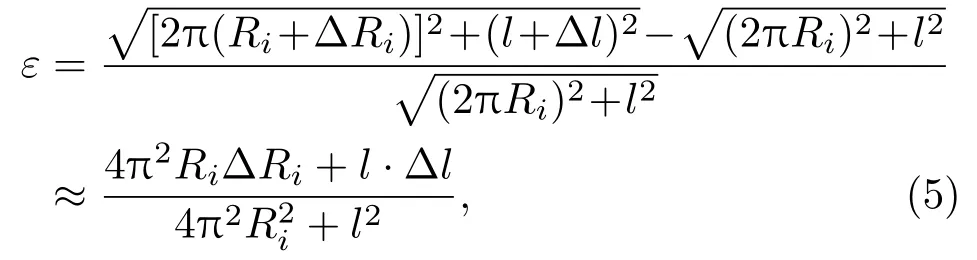
其中Ri,ΔRi分别为波纹薄筒内半径及其变化量,l,Δl分别为波节间距及其变化量,且有,Δl= ΔX/N;σ为轴向位移产生的径向薄膜应力;d为波纹薄筒筒壁厚度;h为波纹薄筒波节高度.(5)式可进一步简化为

对于粘贴长度为L的光纤,轴向应变导致相位变化为[19]

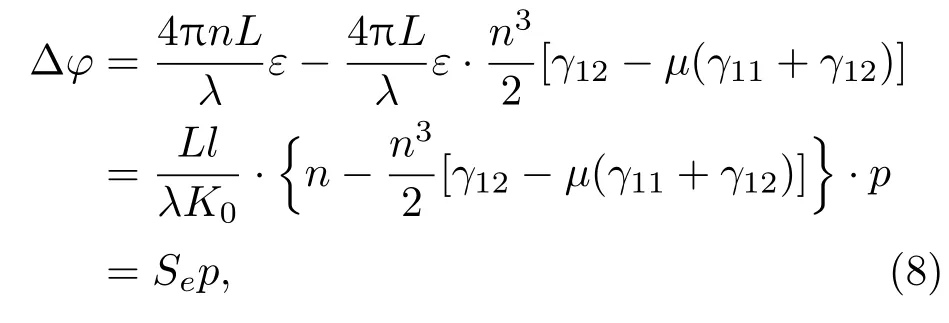
其中,λ为光波长,γ11,γ12为单模光纤弹光系数矩阵元素;µ为室温下石英材料泊松比.其中,

为相位灵敏度.由(8)式可知,相位变化近似随声压线性变化,波纹薄筒的增敏效果与波纹薄筒波节间距l成正比,与波纹筒的单波节轴向刚度K0成反比.当选取波纹薄筒波节间距为10.4 mm,单波节轴向刚度为5.2 N/mm时,声压至应变的传递系数为159.2 nε/Pa,光源波长λ=1550.12 nm,且取γ11=0.121[19],γ12=0.27[19],µ=0.1817[20],粘贴光纤长度L为2 m,探测相位灵敏度Se为2.975 rad/Pa.普通单模光纤直接在声压p作用下,纤芯产生的轴向应变为[19],相位变化为

其中,Ef为室温下石英材料的杨氏模量,Ef=7.787×104N/mm2[20],则单模光纤声压至应变的传递系数为0.0047 nε/Pa,传递系数低33872倍,长度2 m普通单模光纤的相位灵敏度Sef为2.073×10−4rad/Pa,相位灵敏度低14351倍.因此,本文采用的波纹薄筒将声压更有效地转化为光纤应变量,从而提高系统的声传感探测极限和相位灵敏度.

3 实验与结果分析

按图1搭建实验系统.窄线宽激光器发出中心波长1550.12 nm、线宽3 kHz、功率40 mW 的激光,信号光先后进入AOM,EDFA被调制成为移频Δf=40 MHz、脉宽w=50 ns,重复周期T=100µs的移频脉冲光,脉冲光经过环形器进入传感光纤,对光纤中的声信号进行探测,声源频率固定为300 Hz,同时将单点声传感器放置于待测位置进行声压监测.

首先,由于普通单模光纤的灵敏度低,未获得有效信号,增加其传感部分的长度,将长度4.7 m的单模光纤绕制成直径6 cm的光纤环对声信号进行传感.光纤环距离光纤起始位置35 m,将光纤环悬挂在声源前5 cm处,单点声传感器放置于光纤环位置.当光纤环所在位置声压级分别为87.3 dB和99.1 dB时,可以从图3(a)和图3(e)时间距离相位图以及图3(b)和图3(f)距离相位中分辨出声信号在35—40 m之间存在声信号;但是,对比图3(c),图3(d)和图3(g),图3(h)探测得到的强弱两个声信号的时域信号和频谱图,仍能分辨出99.1 dB声信号在300 Hz频率处的被测信号,而87.3 dB声信号被测的频谱中,300 Hz的信号被其他频率噪声所淹没.因此,虽然能够定位低于87.3 dB的声信号,但是其声信号的频率等特征已经无法探测.

我们将2 m长的光纤,螺旋形粘贴在直径10 cm、波节间距10.4 mm、单波节轴向刚度为5.2 N/mm的单端开口波纹薄筒的波谷中,该段光纤距离光纤起始位置35 m,声源方向正对薄筒开口端且距其10 cm远.同时,将单点传感器放置于波纹薄筒开口位置,监测声信号强度.图4为系统探测声压级79.2 dB信号的探测结果,可以看到35 m处存在清晰的300 Hz声信号.

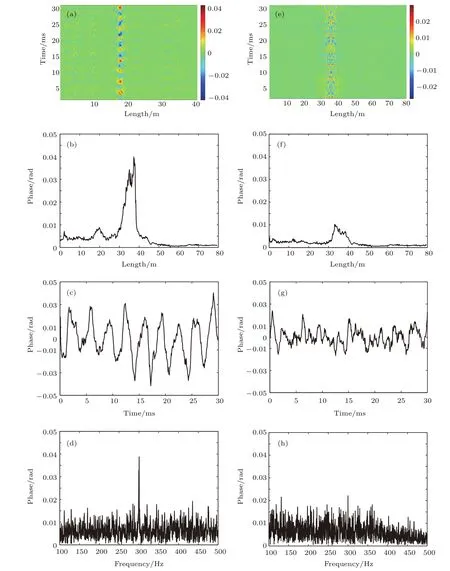
图3 光纤环声传感探测结果 (a)—(d)99.1 d B时信号时间距离等高图、距离相位图、信号时域图和信号频谱图;(e)—(h)87.3 dB时信号时间距离等高图、距离相位图、信号时域图和信号频谱图Fig.3.The results of sound detecting with fiber ring:(a)–(d)Signal contour between time and length,length phase curve,signal time domain picture and signal spectrum with 99.1 dB sound pressure level;(e)–(h)signal contour between time and length,length-phase curve,signal time domain picture and signal spectrum with 87.3 dB sound pressure level.

图4 声压级79.2 dB时的声增敏传感结果 (a)信号时间距离等高图;(b)信号时域图;(c)距离相位图;(d)信号频谱图Fig.4.The sensing result with 79.2 dB sound pressure level:(a)Signal contour between time and length;(b)signal time domain picture;(c)signal length-phase curve;(d)signal spectrum.

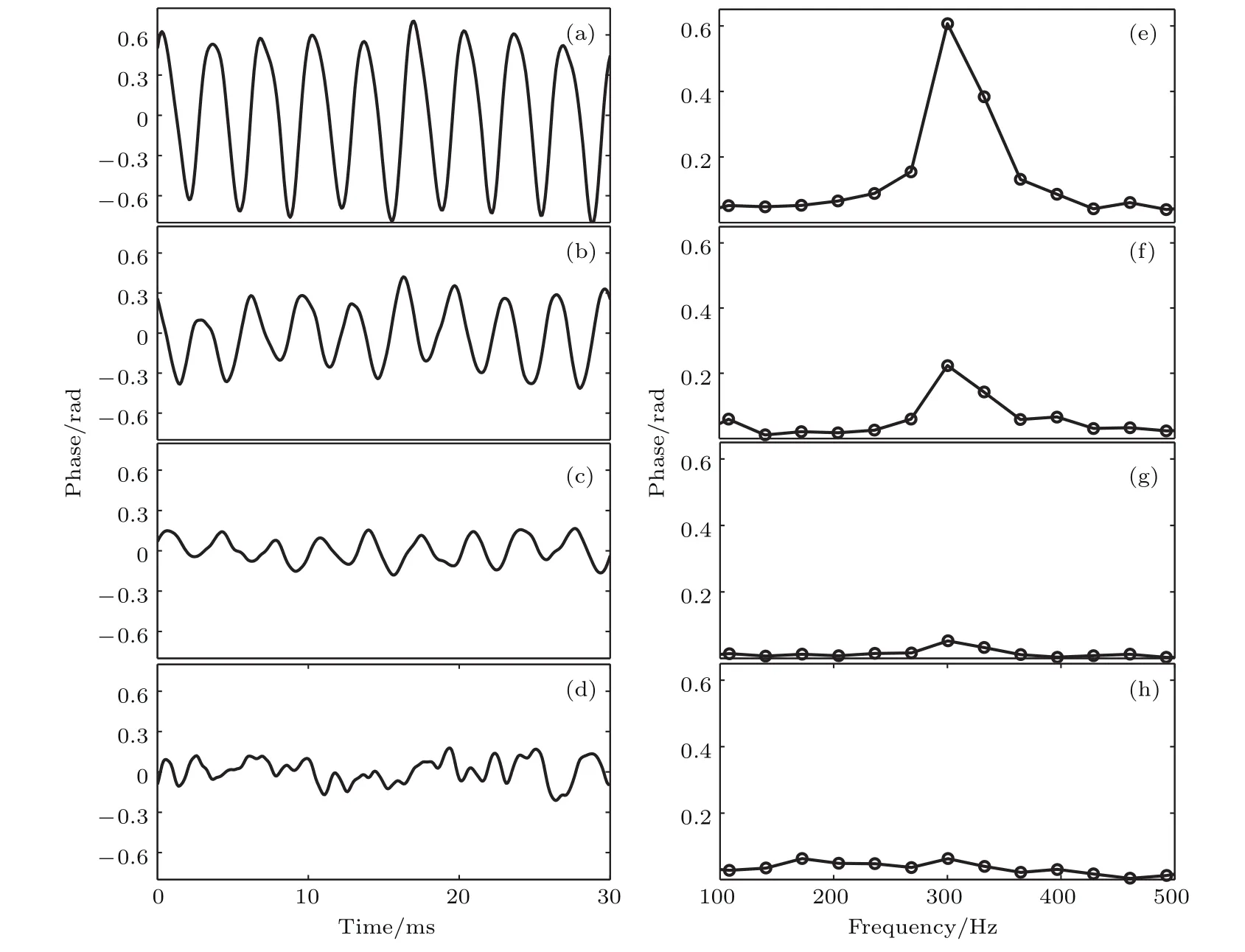
图5 声增敏传感系统探测声信号时域图和频谱图 (a)—(d)84.6 dB,76.3 dB,60.1 dB,54.3 dB时域图;(e)—(h)84.6 dB,76.3 dB,60.1 dB,54.3 dB频谱图Fig.5.The time domain pictures and spectrum from acoustic detection enhancement:(a)–(d)Time domain picture with 84.6 dB,76.3 dB,60.1 dB,54.3 dB;(e)–(h)spectrum with 84.6 dB,76.3 dB,60.1 dB,54.3 dB.

表1 3种声增敏传感器主要参数Table 1.Main parameters of three kinds of acoustic sensors.

依次从 84.6 dB至 54.3 dB(对应声压从339.6 mPa至 10.4 mPa)改变声源强度,进行声信号探测,并通过傅里叶变换得到信号频谱图.图5为不同声压下,35 m位置处探测得到声信号时域波形及其频谱.图中声压级分别为84.6,76.3,60.1,54.3 dB,对应声压为339.6,130.6,20.2和10.4 mPa.图5显示,在60.1至84.6 dB声压级范围内正弦信号波形清晰,幅值随声压降低而减小,而在声压级为54.3 dB时,被探测的声信号已淹没于噪声中.

图6所示为35 m位置处探测得到声信号频谱幅值随声压变化的关系.从图6可以看到,在声压20.2—339.6 mPa部分,信号幅值随声压近似成线性关系;从图6插图中可以看到声压小于20.2 mPa时,信号幅值几乎不随声压变化,表明系统最小探测声压级为60.1 dB.相比未经增敏的光纤环,最小探测声压级显著提升.

我们进一步对3个不同参数的声增敏传感装置进行实验.由(8)式可知,声传感增敏效果与传感光纤长度L、波纹薄筒的波节间距l和单波节轴向刚度K0有关,故选取波节间距相近、单波节轴向刚度不同的波纹薄筒,设计制作了3种灵敏度不同的声增敏传感器,其主要参数列于表1.

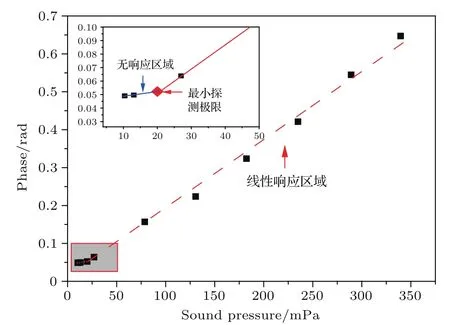
图6 探测声信号频谱幅值与声信号声压的关系(插图为局部放大图)Fig.6.The relationship between signal’s spectrum amplitude and the sound pressure,the illustration is the zoomed in picture.

图7 3种声增敏传感装置对比实验原理图、时间距离相位图和灵敏度拟合结果 (a)实验原理图;(b)信号时间距离等高图;(c)灵敏度拟合结果Fig.7.The principle diagram experimental result and fitting result of the compared experiment among three devices:(a)The principle diagram;(b)contour between time and length;(c)the fitting result.

将3种声增敏传感装置按图7(a)所示依次连接入光路,1号传感装置距光纤起始端44 m,2号与1号传感装置、3号与2号传感装置间分别连接25 m和23 m光纤,传感装置固定在距声源10 cm处,开口端正对声源.同时将单点声传感器放置于波纹薄筒开口端监测声信号强度.改变声源强度,3个声增敏传感装置同时进行探测.

图7(b)所示为3种声增敏传感装置的时间距离相位图,图中分别在45 m,70 m和93 m位置传感到声信号.图7(c)为幅值声压测试结果,可看到幅值随声压变化具有良好的线性度,线性拟合R2分别为0.9984,0.9990和0.9992;三种声增敏传感装置的相位灵敏度测量值分别为1.80,1.22和0.68 rad/Pa,相比3号传感器,1号和2号声增敏传感装置的相位灵敏度分别增加2.712倍和1.758倍.三种声增敏传感装置的相位灵敏度理论计算值为2.975,1.929和1.097 rad/Pa;相比3号传感器,1号和2号声增敏传感装置的理论相位灵敏度分别增加2.647倍和1.794倍.相位灵敏度实验结果与理论计算值存在差异,但趋势一致,这可能由于实际中的部分参数偏离理论值,但是声增敏传感装置间的比值关系基本一致.因此建立的模型可用于实现灵敏度的灵活设计,指导声增敏装置的声增敏传感装置几何尺寸和不同材料选择.

4 结 论

本文提出了一种基于C-OTDR光纤分布式声增敏传感方法,采用单端固定开口的增敏薄筒转化声压为光纤应变.建立声压至光纤应变传递模型用于分析单端固定开口的增敏薄筒的增敏机理,给出了相位灵敏度与声增敏传感装置的波节间距、单波节轴向刚度等几何参数和力学参数的关系,理论分析表明增敏薄筒能有效提高声传感灵敏度.搭建声增敏传感系统进行测量实验,结果表明声增敏传感装置最小探测声信号达到60.1 dB,3种规格声增敏传感装置灵敏度变化趋势基本符合理论计算结果,并且灵敏度之间比值与计算值一致.该声增敏传感系统有效提高了声传感相位灵敏度,通过改变增敏参数可实现灵敏度的灵活设计.研究结果为高灵敏度的光纤分布式声传感的进一步发展提供了理论和实验基础.

[1]Teixeira J G V,Leite I T,Silva S,Frazão O 2014Photon.Sens.4198

[2]Wild G,Hinckley S 2008IEEE Sens.J.81184

[3]Takahashi N,Hirose A,Takahashi S 1997Opt.Rev.4691

[4]Wang S,Lu P,Liao H,Zhang L,Liu D,Zhang J 2013J.Mod.Opt.601892

[5]Sakai T,Suzuki S,Wakayama S 2016Exp.Mech.561439

[6]Moccia M,Pisco M,Cutolo A,Galdi V,Bevilacqua P,Cusano A 2011Opt.Express1918842

[7]Guo F,Fink T,Han M,Koester L,Turner J,Huang J 2012Opt.Lett.371505

[8]Wei P,Shan X,Sun X 2013Opt.Fiber Technol.1947

[9]He H,Shao L,Li Z,Zhang Z,Zou X,Luo B,Pan W,Yan L 2016Sensors-Basel16681

[10]Hussels M T,Chruscicki S,Habib A,Krebber K 2016In Sixth European Workshop on Optical Fibre Sensors(EWOFS’)Limerick,Ireland,May 30,2016 p99162Y

[11]Palmieri L,Schenato L 2013The Open Opt.J.7104

[12]Lu Y,Zhu T,Chen L,Bao X 2010J.Lightwave Technol.283243

[13]Wu Y,Gan J,Li Q,Zhang Z 2015IEEE Photonics J.71

[14]Shang Y,Yang Y,Wang C,Liu X,Wang C,Peng G 2016Measurement79222

[15]Wang D H,Jia P G,Ma Z G,Xie L F,Liang Q B 2014Electron.Lett.50649

[16]Wang C,Shang Y,Liu X,Wang C,Peng G D 2014Asia Communications and Photonics ConferenceShanghai,China,November 11–14,2014 pATh3A-213

[17]Iida D,Toge K,Manabe T 2016Optical Fiber Communications Conference and ExhibitionAnaheim,California United States,March 20–22,2016 pM2D-6

[18]Luo W 2006M.S.Dissertation(Qinhuangdao:Yanshan University)(in Chinese)[骆伟 2006硕士学位论文 (秦皇岛:燕山大学)

[19]Lü D C,Zhang X P 2010Acta Opt.Sin.251025(in Chinese)[吕丁成,张晓萍 2010光学学报 251025]

[20]Zhao L J 2010Acta Phys.Sin.596219(in Chinese)[赵丽娟2010物理学报596219]