基于相场模型的一维拉杆脆性断裂分析

袁集海，陈昌萍†

（1.厦门大学建筑与土木工程学院，福建厦门 361005；2.厦门理工学院土木工程与建筑学院，福建厦门 361024）

上世纪末，Francfort 和Marigo[1]基于能量最小化原理，提出了解决固体结构断裂损伤的变分方法.该方法认为裂纹的出现和演化使总势能最小，其实质是从能量变分的角度对Griffith[2]脆性断裂理论的发展和推广，然而在连续介质力学框架下求解过程中仍然存在位移不连续带来的求解困难，该工作为二阶相场模型的建立奠定了理论基础.Bourdin[3]等在断裂变分方法的基础上，通过引入在0 到1 之间连续变化的相场变量d-来表征裂缝的起裂和延伸，同时引入裂缝宽度参数l 来控制裂缝的弥散程度.随后，Miehe[4]等建立了与热力学自洽的二阶相场损伤模型.二阶相场模型的完善迅速吸引了一大批国内外学者的关注，为后续相场损伤模型的发展做出了重要的贡献.Borden[5]等提出了四阶相场损伤模型并采用等几何法对耦合方程进行求解，另外，还研究了动态脆性断裂[6]和塑性材料[7]断裂问题.邓俊俊[8]采用无网格相场模型研究了复杂边坡破坏问题.张飞[9]基于自适应移动网格方法优化了相场模型并模拟了水力裂缝延伸过程.付禹铭[10]针对各向异性损伤相场模型提出了新的投影算子算法.仇杰峰[11]和庄洛嘉[12]采用相场损伤模型研究了混凝土破坏问题.

相场损伤模型采用连续方法来描述不连续问题，与传统求解断裂问题方法相比具有一定的优势[13-14].本文以受拉结构为研究对象，采用相场损伤模型数值模拟了无缺陷杆、含几何缺陷杆以及含损伤杆应变局部化行为和脆性断裂行为.

1 相场损伤模型

考虑一维杆断裂问题，其长度和截面分别为L和A.假设杆在x∈Γd处断裂，其他地方完好无损，并引入相场变量d（x）来描述杆的破坏状态，则该变量分布（如图1（a）所示）为

为了便于数值计算，引入如下形式的指数函数来逼近上述不连续函数分布，即

式中：l 为正则化参数，该参数可以控制相场变量的分布区域，如图1（b）所示，正则化参数越小，相场变量分布区域也越小，当l 趋近于0 时，该连续函数分布趋近于上述不连续函数分布.显然，式（2）是如下微分方程的解[4].

且满足下列边界条件

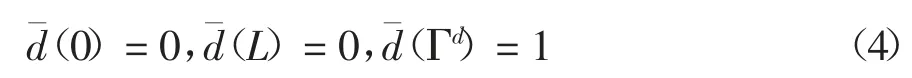
对方程（3）运用变分原理再在整个域内积分可构建相应泛函

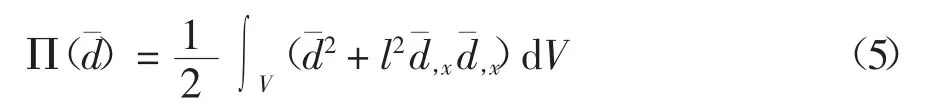
且在整个积分域内满足dV=Γdx，则

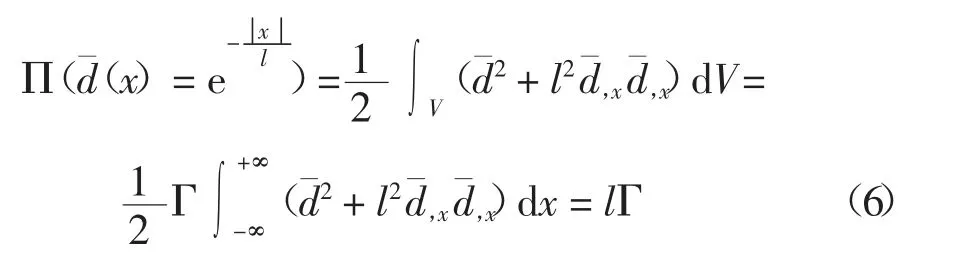
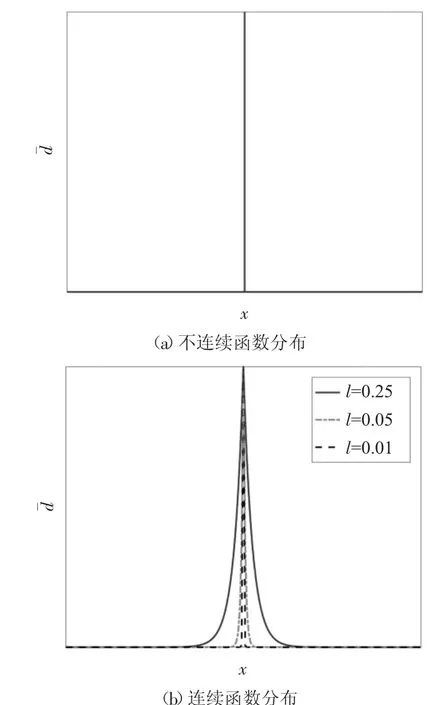
图1 相场变量分布Fig.1 Distribution of phase field

因此，断裂面Γ 可用裂缝分布函数近似表示为

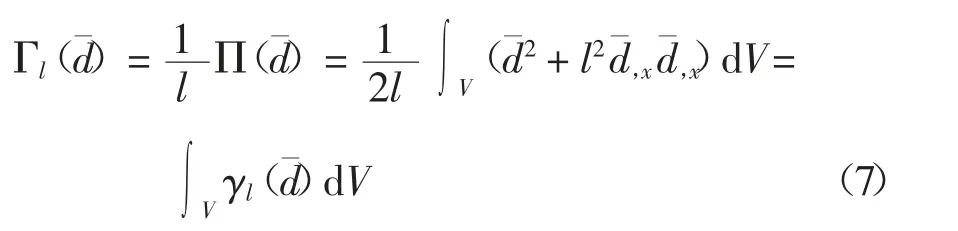
该函数描述了断裂面处裂缝的分布情况.引入裂缝分布密度函数

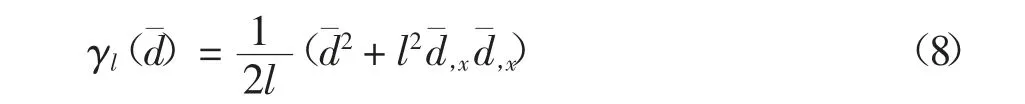
对于多维断裂问题，在求解域Ω 内相应裂缝分布函数和裂缝分布密度函数分别为

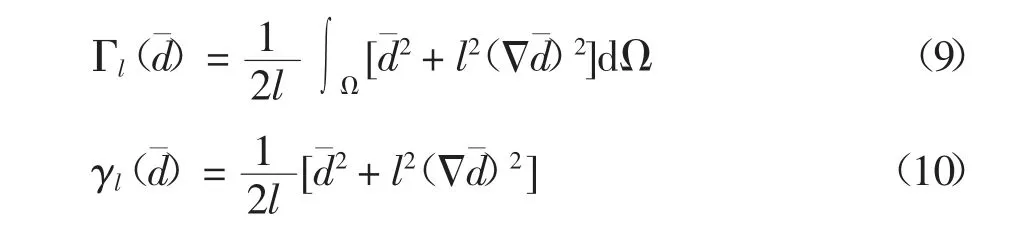
基于格里菲斯断裂理论，弹性体在单位面积上耗散的能量为Gc，则在断裂面处Γl（d）结构断裂耗散能量[8].

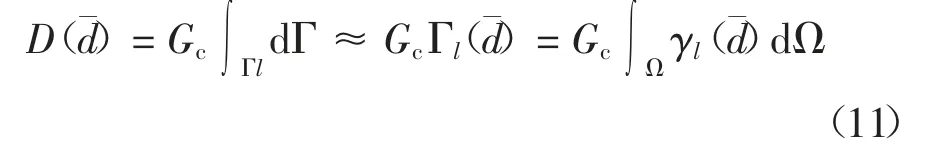
在不考虑动能的情况下，根据能量守恒定律，弹性体总能量变化率为0，即

将式（13）～（15）代入能量守恒方程即可得到相场损伤模型控制方程

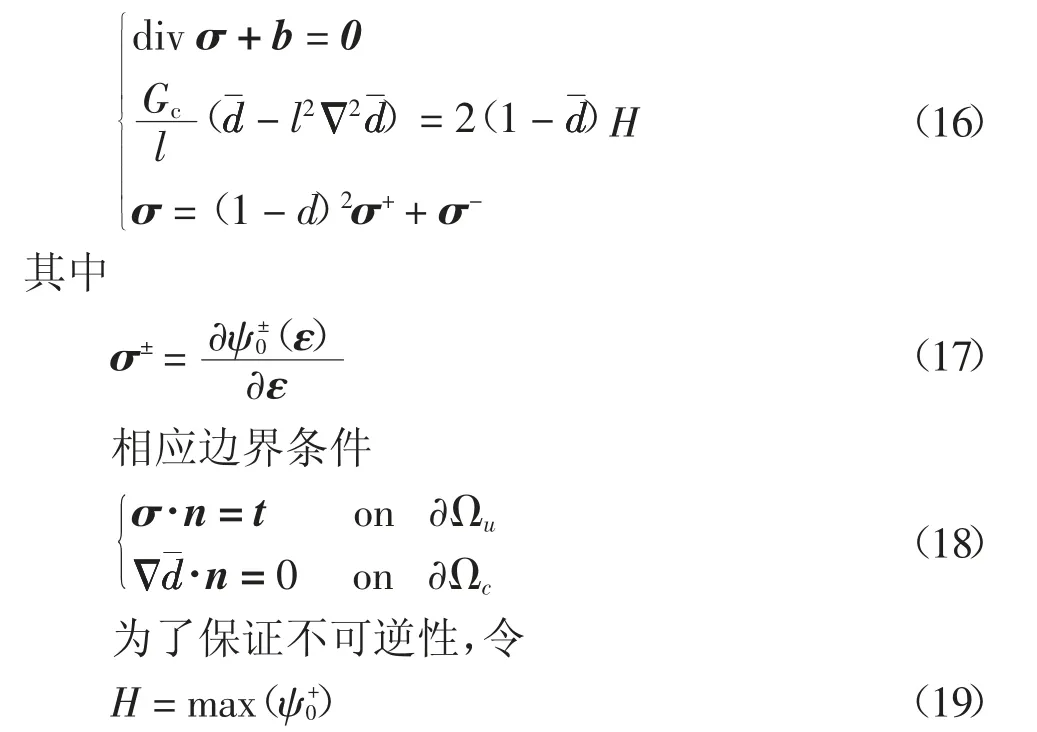
采用有限元方法对方程（16）进行数值求解，平衡方程伽辽金弱形式

采用线性单元对相场和位移场及其相应增量进行离散化

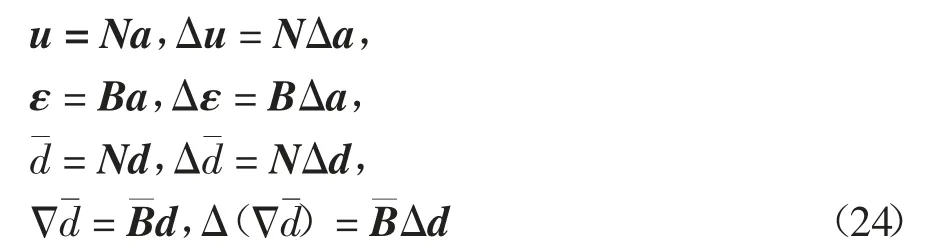
式中：N、B 分别为形函数和梯度矩阵；a、d 为节点位移和相场.将式（24）代入弱形式和增量方程，并将所得结果代入方程（23）可得增量迭代方程组.本文采用交错最小算法[15]，故忽略耦合刚度后的迭代方程组为

式中：刚度矩阵和节点力向量分别为

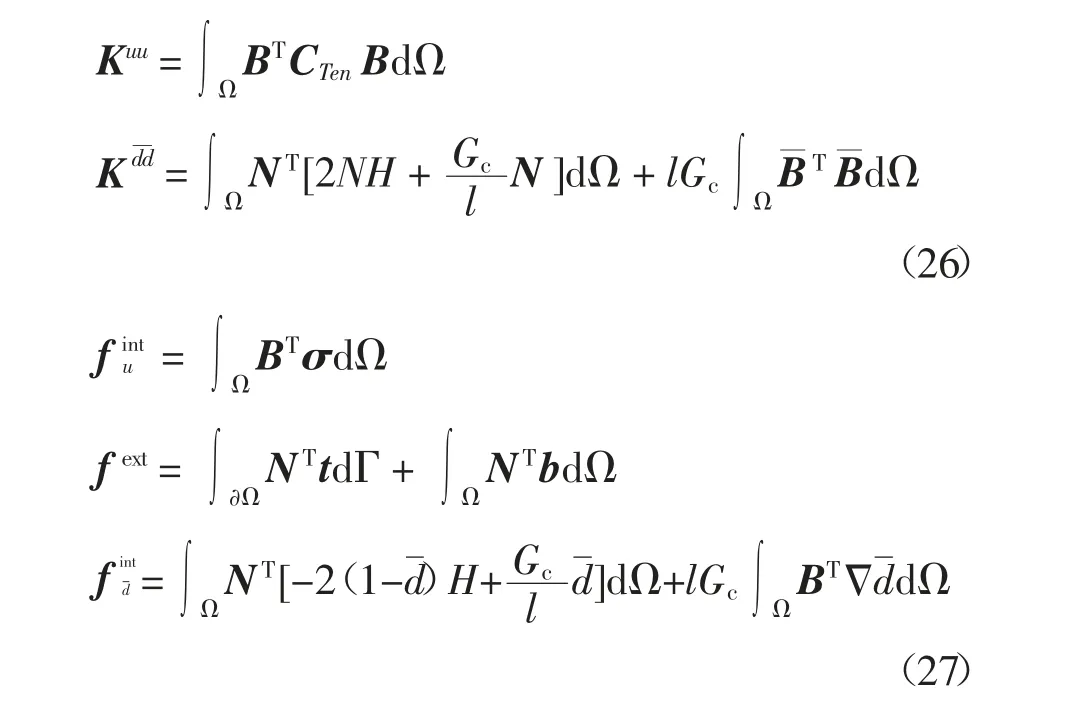
2 结果与讨论

考虑如图2 所示一维受拉杆，其长度L=100 mm，截面面积A=4 mm×4 mm，左端固定，右端施加位移荷载u（L），不计体力.若无特别说明，弹性模量E=210 GPa；泊松比υ=0.3；正则化参数l=0.2 mm；断裂能释放率Gc=2.7 × 10-3kN/mm.本节通过三个数值算例分析一维受拉杆结构脆性破坏.

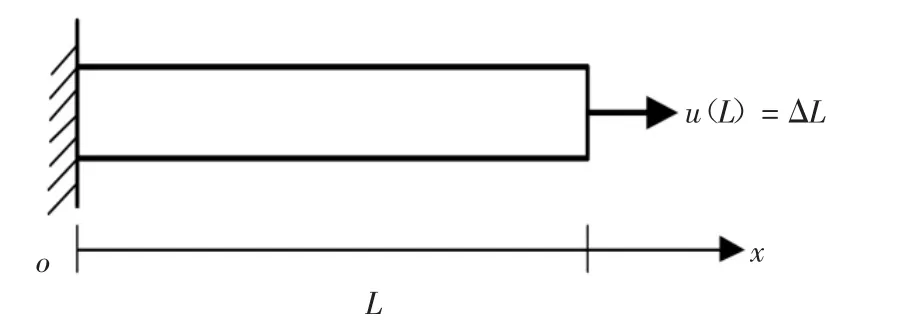
图2 一维受拉杆Fig.2 One dimensional bar under tension

2.1 无缺陷受拉杆

对于如图2 所示无缺陷受拉杆，由于应变和相场均匀分布，故可忽略控制方程中相场变量梯度项，即可得到解析解.图3 给出了荷载位移曲线有限元解和解析解，其中，虚线为解析解，实线为有限元解.对于有限元解，当位移荷载超过临界荷载后，曲线垂直下降到0，这是因为杆发生了脆性断裂，开裂后，内力立即减小为0.而对于解析解，曲线上升阶段与有限元解保持一致.另外，值得指出的是解析解曲线只有上升阶段才有意义，脆性断裂无软化阶段.

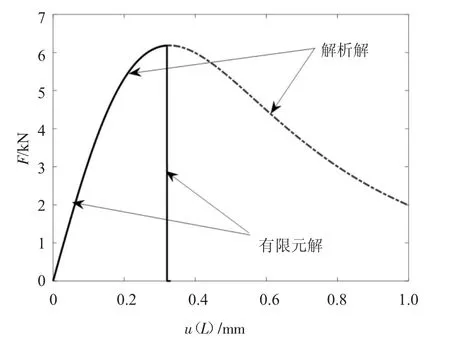
图3 有限元解与解析解对比Fig.3 Comparision beween numerical solution and analytical solution

2.2 含几何缺陷受拉杆

本节第二个数值算例为含缺陷受拉杆，其长度为L=10 mm，截面面积为A=1 mm×1 mm；中间部分为弱化区，长度为l0=1 mm，截面积为A′=0.9A，如图4 所示.由解析解可以得到临界位移荷载uc=0.032 7 mm；加载过程荷载步长Δu=uc/2 000.

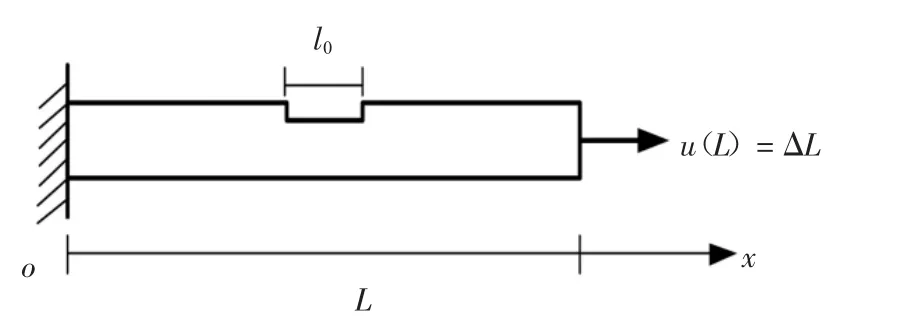
图4 含几何缺陷受拉杆Fig.4 One dimensional bar with geometric imperfection under tension

图5 给出了含缺陷杆（实线）和无缺陷杆（虚线）荷载位移曲线，从图中可以看出曲线上升阶段二者保持一致，下降阶段无缺陷杆最大内力和临界位移荷载均大于含缺陷杆最大内力和临界位移荷载.图6给出了不同荷载步n 相场、应变和位移分布，其对应荷载位移点如图5 所示.当位移荷载较小（n=500）时，相场和应变均匀分布，位移线性分布；当位移荷载接近临界位移荷载时，相场和应变开始局部化，其分布集中在弱化区，且在该区位移不再线性分布.当位移荷载超过临界荷载（n=1 889）时，在杆中点处发生断裂（相场在该点达到1，应变趋于无穷大，位移均匀分布：左侧位移为0，右侧位移为所施加位移荷载）.

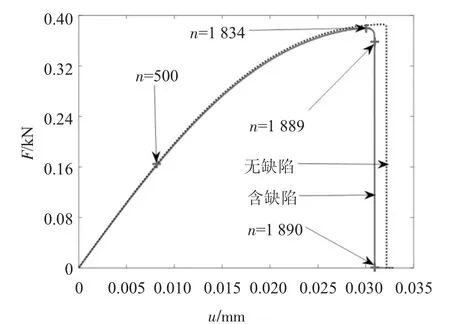
图5 荷载位移曲线Fig.5 Load deflection curve

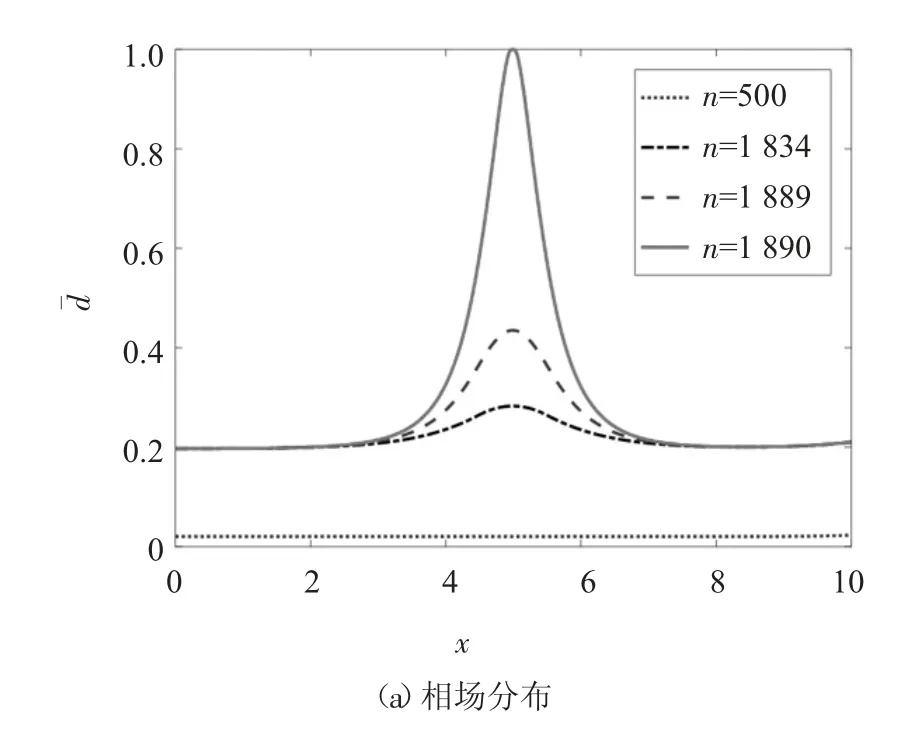
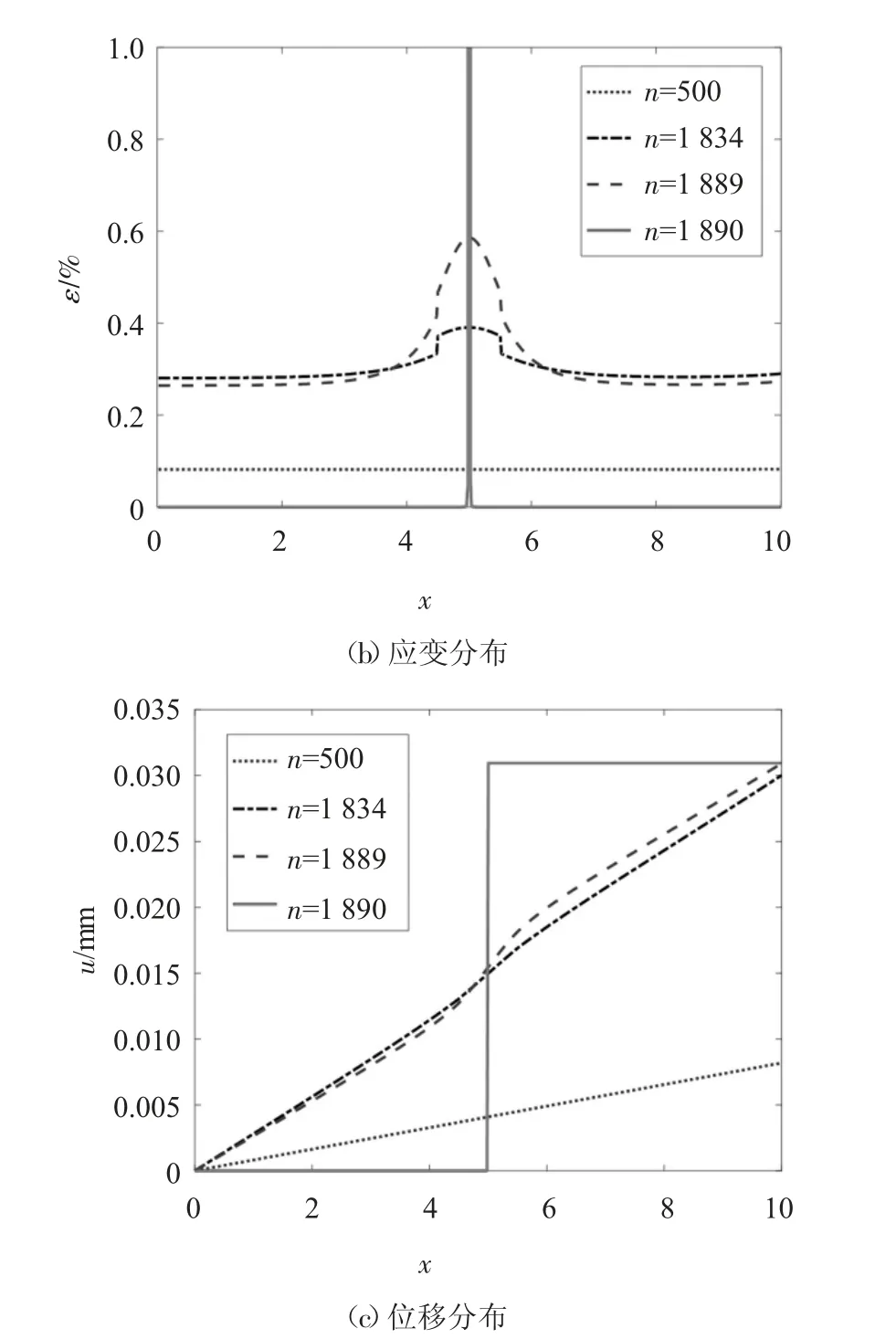
图6 相场、应变和位移演化Fig.6 Evolution of phase field，strain and displacement

2.3 损伤受拉杆

类似损伤力学中损伤变量的概念，可以将相场变量视作量化结构损伤指标.本节最后一个算例在杆中点预设相场变量，如图7 所示.其他材料参数和几何参数同算例2，荷载步Δu=uc/4 000.

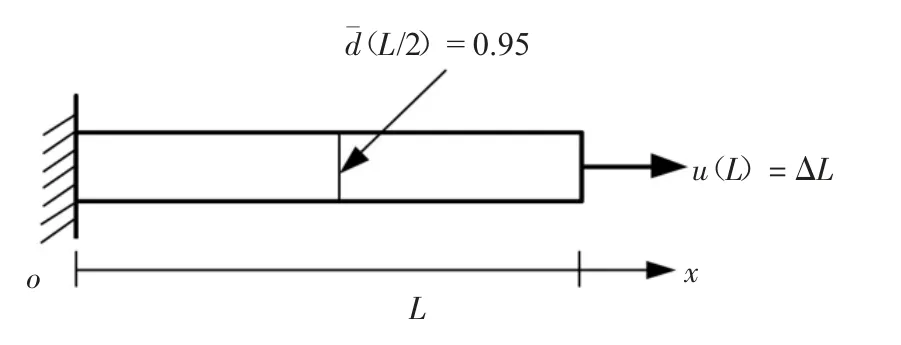
图7 损伤受拉杆Fig.7 One dimensional bar with damage under tension

图8 给出了损伤受拉杆荷载位移曲线，由于杆在中点处发生了严重的损伤，损伤杆临界位移荷载和最大内力明显远小于无损伤杆临界位移荷载和最大内力.图9 给出了不同荷载步n 相场、应变和位移分布，其对应荷载位移点如图8 所示.与含几何缺陷杆不同的是，位移荷载较小时，预设损伤变量会导致杆结构发生局部化现象，如图9 所示.

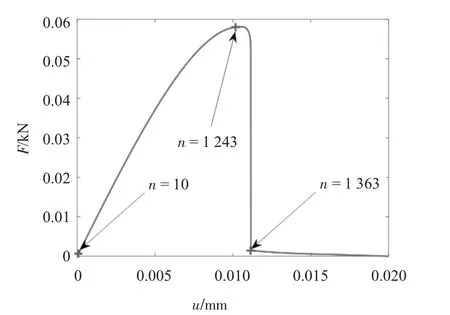
图8 荷载位移曲线Fig.8 Load deflection curve

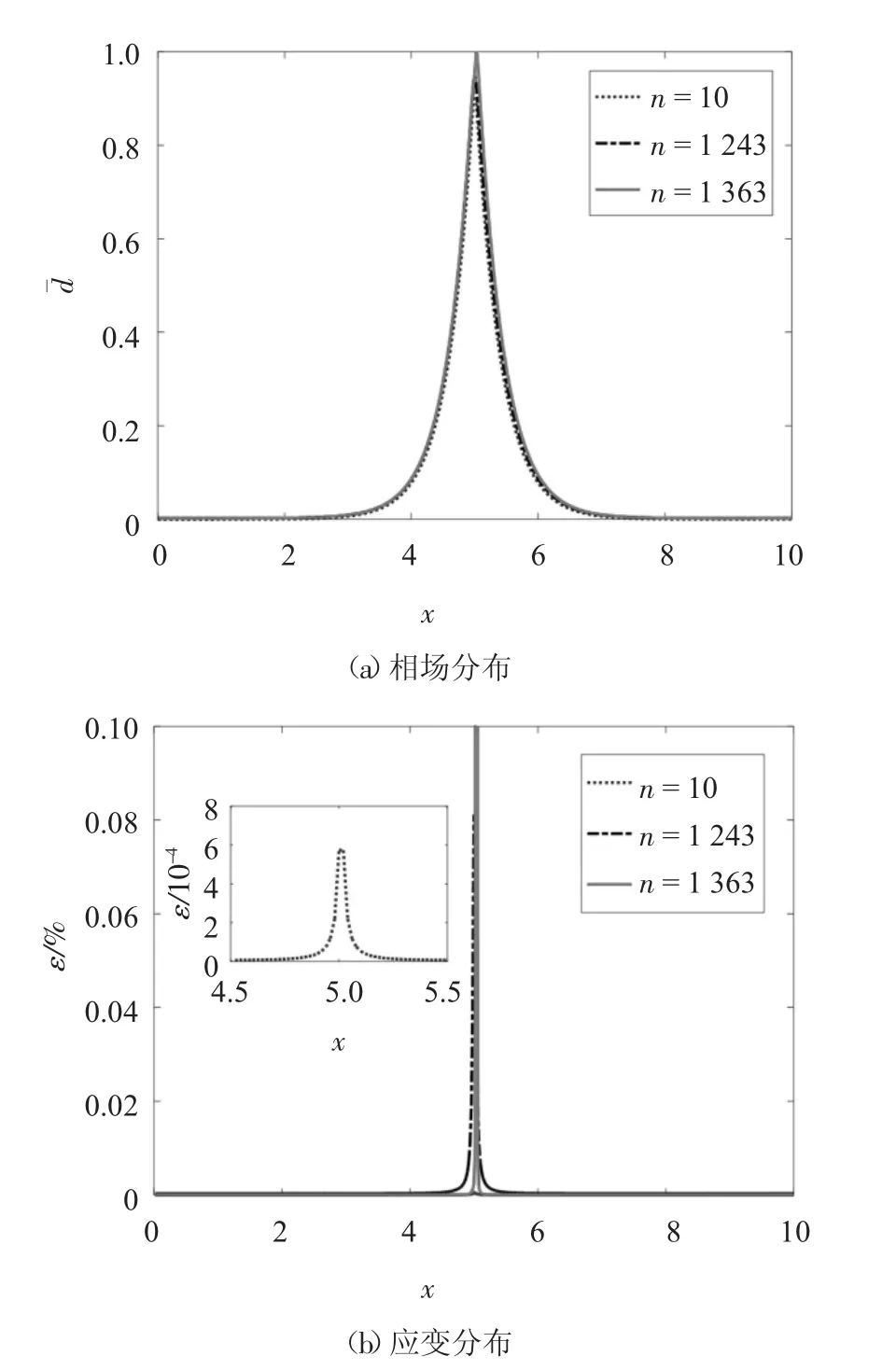
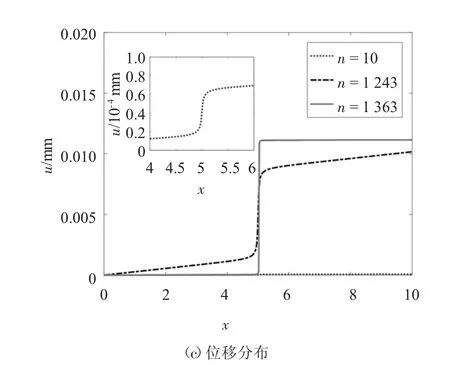
图9 相场、应变和位移演化Fig.9 Evolution of phase field，strain and displacement

3 结论

基于相场模型，本文采用有限元数值方法通过三个数值算例分析了一维受拉杆在位移荷载下脆性断裂破坏.算例一模拟了无缺陷杆受拉断裂破坏，并将数值解与解析解对比，论证了数值解的正确性.算例二和算例三分别分析了含几何缺陷杆和损伤杆受拉破坏.计算结果表明有限元相场分析方法能够较准确地模拟破坏区应变局部化行为和破坏演化过程.