广义线性混合模型及其在非寿险信度费率厘定中的应用

康萌萌

(山东财经大学 保险学院，山东 济南 250014)

一、引 言

在非寿险费率厘定中，常用广义线性模型对保险标的进行分类，并且厘定每个风险类别的费率。但是，随着时间的推移，这样划分的风险类别仍然存在异质性，有的保险标的实际索赔高于模型预测值，有的则低于模型预测值，如果仍然按照这种分类收取保费，则会对索赔经验少的保险标的收取相对较高的保费，从而导致逆选择问题。为了避免这种情况，应该利用新索赔经验对原来的费率进行调整，信度理论主要研究这个问题。

信度理论是非寿险重要的定价方法，主要包括有限波动信度理论和最精确信度理论。有限波动信度理论假设随机因素是造成经验数据波动的最主要原因。为了克服该理论的不足，1950年Arthur Bailey利用贝叶斯方法研究信度理论，开创了最精确信度理论。1967年Bühlmann在贝叶斯理论框架下，提出最简单的线性信度模型。随后，学者不断改进该模型，提出Bühlmann-Straub和Hachemeister回归等信度模型。Frees 等证明线性信度模型等同于线性混合模型，并在此框架下推导出线性信度模型结构参数和信度保费的预测值[1]。线性混合模型是将随机效应加入普通线性回归模型的均值方程中来处理变量间的相关性，因此其因变量服从正态分布。但在精算中，损失次数数据为离散型分布，损失金额模型为右偏分布，都不服从正态分布，大大限制线性混合模型在非寿险精算中的应用。广义线性混合模型将线性混合模型的因变量推广到指数分布族，大大提高其在精算建模中的灵活性。目前这类模型在非寿险精算中有着广泛的应用。Antonio 和Beirlant利用因变量服从伽玛分布和泊松分布的广义线性混合模型对信度理论进行建模，并进行实证分析[2]。Fred在广义线性混合模型的框架下，讨论了信度费率厘定问题[3]。Ohlsson 和 Johansson利用迭代算法将广义线性模型和信度模型相结合，建立多水平费率因子厘定模型[4]。

国内，贺宝龙等和康萌萌假设因变量服从泊松分布、过离散泊松和负二项分布，基于广义线性混合模型对非寿险信度保费进行厘定[5-6]。谢远涛等利用广义线性混合模型研究非寿险信度模型，并以特例形式利用同时考虑先验和后验信息的Tweedie模型重新构建经典Bühlmann和Bühlmann-Straub信度模型[7]。张连增和孙维伟利用因变量服从泊松分布的广义线性混合模型对汽车保险费率进行厘定，并用R软件进行实证分析[8]。康萌萌和孟生旺在广义线性混合模型框架下，利用MCMC模拟和伪似然估计法对因变量服从伽玛分布和逆高斯分布的交叉分类信度模型进行估计[9]。李政宵和孟生旺建立具有空间效应的零膨胀贝叶斯分层模型，并对模型中连续型协变量引入惩罚样条函数来描述非线性效应，并将其用于非寿险索赔频率预测，研究表明该模型优于传统的广义线性模型[10]。

从上面的分析来看，国内外学者对混合效应模型在非寿险费率厘定中的应用进行大量深入的研究，但他们的研究中存在一个问题，即在研究索赔次数时，对因变量的推广仅仅推广到负二项分布。本文在前人的研究基础上，将因变量推广到广义泊松、负二项K分布、双泊松分布，然后运用极大似然估计中的限制性虚拟似然法和自适应高斯求积法对参数进行估计，最后用美国劳工补偿保险进行实证分析，比较模型拟合效果，得到最优模型。

二、理论模型

(一)线性混合效应模型下的信度模型

根据Frees 等构建的Bühlmann信度模型表达式为：

yit=β+αi+εit

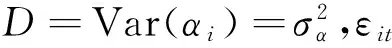
在此框架下，将因变量yit推广到指数分布族，即可得到广义线性混合模型，可以利用其研究信度模型结构参数估计和信度保费预测。

(二)广义线性混合模型

广义线性混合模型是在广义线性模型的基础上将随机效应引入均值方程中来处理重复测量之间的相关性，其构成与广义线性模型相似，也是由随机成分、系统成分和连接函数三部分构成。随机成分假设因变量服从指数分布族；系统成分为线性预测部分，随机效应体现其中；连接函数为连接系统成分和随机成分的函数，一般采用对数连接。

假设Yit表示第i个风险类别第t年的索赔观测值。若给定随机效应bi，Yit来自指数分布族，则其密度函数为：

其中，φ(·)和c(·)为给定函数，θ为自然参数，φ为尺度参数。随机效应bi给定的条件下，其因变量的均值和方差是一个条件函数：

μij=E[Yit|bi]=φ′(θit)

Var[Yit|bi]=φφ″(θit)=φV(μit)

其中，V(·)是E[Yit|bi]的函数；φ为离散参数(残差变异)。在广义线性混合模型中，连接函数是连接均值和线性预测部分的函数，与广义线性模型相同。

其中，g(·)为连接函数，β(p×1)表示固定效应，bi(q×1)表示第i个风险类别的随机效应。Xi(ni×p)和Zi(ni×q)分别表示固定效应和随机效应的设计矩阵。

(三)实证模型构建

本文构建7种广义线性混合模型进行实证分布，区别主要在于随机成分不同。

1.泊松广义线性混合模型。泊松分布是最常见的拟合非寿险索赔次数的分布。若Yit表示第i个风险集合在第t年的索赔次数，则其泊松分布的概率密度函数为：

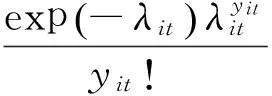
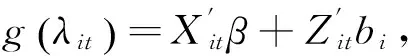
2.过离散泊松广义线性混合模型。泊松分布的均值等于方差，但在精算中，损失次数数据通常方差大于均值，即存在过离散问题。此时，可以将离散参数引入泊松分布方差函数中来对过离散进行调整。

Var(Yit)=φλit

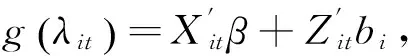
3.负二项广义线性混合模型。负二项分布也是调整过离散问题的常用方法。根据方差和均值的关系，负二项分布可以分为负二项Ⅰ、负二项Ⅱ和负二项K三种分布，分别记为NBⅠ、NBⅡ和NBK。

(1)NBⅠ

NBⅠ分布(Cameron 和Trivedi，1986)的概率密度函数为：

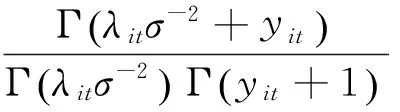
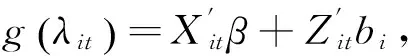
(2)NBⅡ

NBⅡ分布(Cameron 和Trivedi,1986)的概率密度函数为：

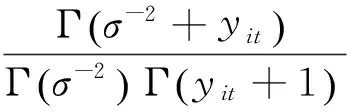
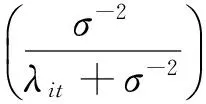
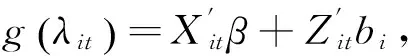
(3)NBK

NBK分布的概率密度函数为：

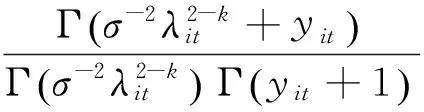
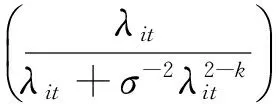
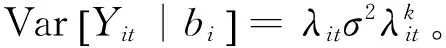
4.广义泊松广义线性混合模型。广义泊松分布(Wang 和Famoye,1997)的概率密度函数为：

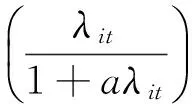
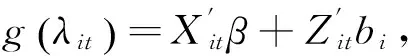
5.双泊松广义线性混合模型。双泊松分布的概率密度函数为：

Pr[Yit=0|bi]=θ1/2e-θ2λit

Pr[Yit=yit|bi]=

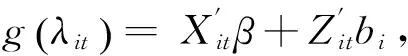
(四)参数估计

本文采用限制性虚拟似然法和自适应高斯求积法对广义线性混合模型进行参数估计。

1.限制性虚拟似然法。Yi为第i个对象的观测向量。假设随机效应bi～N(0,D)，Yi的条件协方差矩阵定义为：

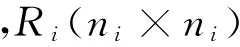
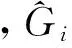
vi=Xiβ+Zibi+εi

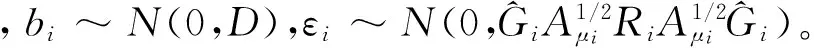
2.自适应高斯求积法。Lin 和Pierc(1994)给出了利用高斯求积解混合模型的具体计算过程。首先考虑单一随机效应bi的情况，第i个个体对边际似然率的贡献为：

其中，假设随机效应bi服从均值为0，标准差为σ的正态分布。令δi=σ-1bi，可以表示为：

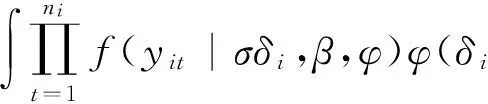
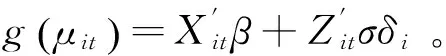
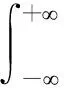
Q表示近似阶数，zq表示第Q阶第厄密多项式，wq表示相应的权重。Abramowitz和Stegun(1972)将节点zq和权重wq制成了表格。

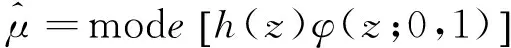
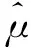
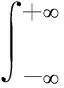
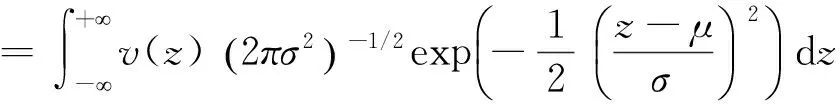
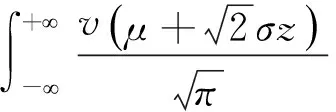
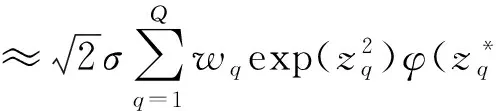
L(β,α,φ；y)≈

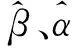
三、实证分析

(一)数据来源

本文利用劳工补偿保险数据(Klugman，1992)进行实证研究。该数据的风险单位数为经过通货膨胀调整的工资总额，原数据中共有133个风险集合连续7年的索赔次数，其中有5个风险集合含有缺失值，将其删除，共得到128个风险集合连续7年的索赔次数数据。每年索赔次数随时间变化的轨迹图如图1所示。

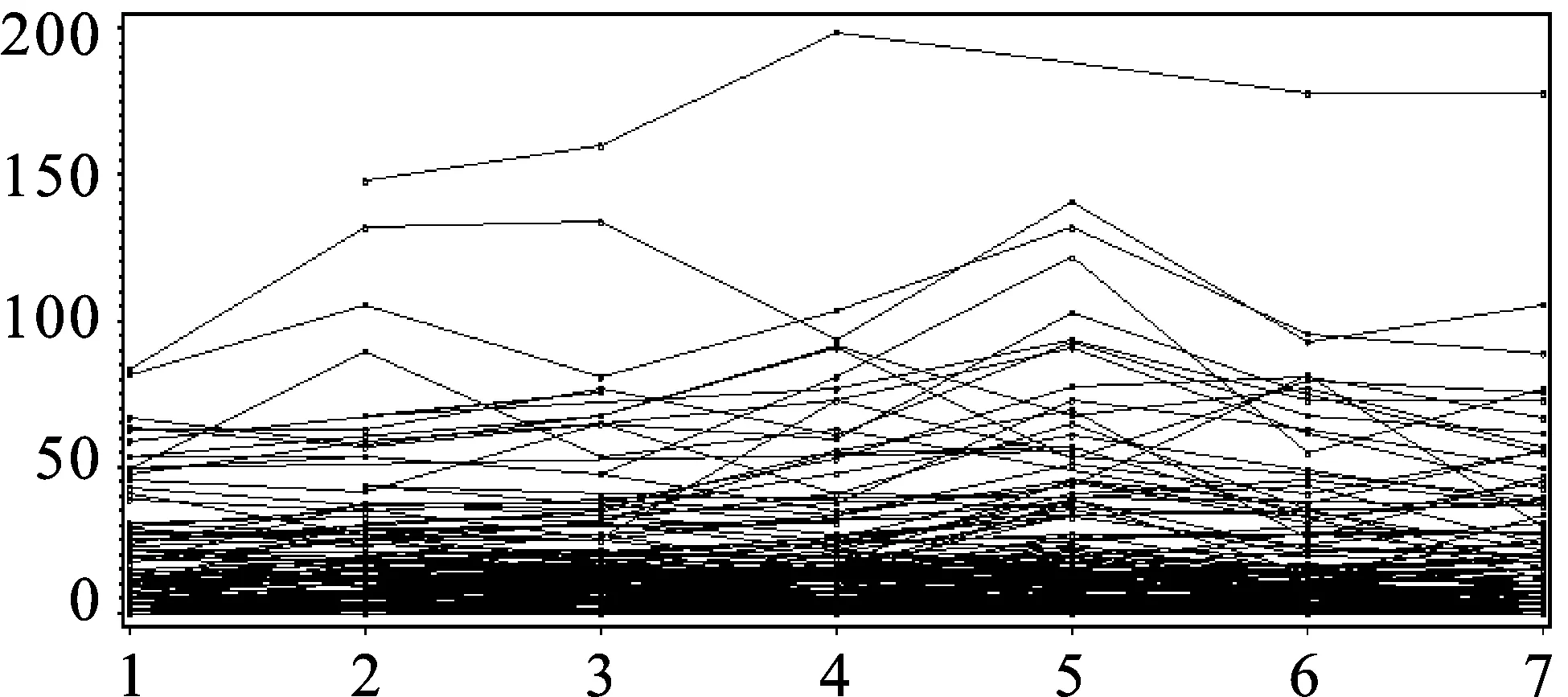
图1 索赔次数随时间变化轨迹图

图1表明，每个风险集合在不同年份索赔次数观测值具有较高的相关性，即第一年索赔次数较高的风险集合在随后几年的索赔次数也较高，第一年索赔次数较低的随后几年索赔次数也较低。每个风险集合的索赔变化率也不相同，即有的风险集合索赔增长率较高，有的风险集合增长率较低，还有一些没有显著变化。从图1中还可以看出，每个风险集合的组内差异和组间差异随时间推移都有所增大。因此，建模分析时，既要考虑各个风险集合的同质性，又要考虑风险集合组间异质性和非常数方差等问题。为了研究组间和组内的变异性，给出随机效应模型的四种均值方程：

模型1：log(λit)=log(Payrollit)+β0+bi,0

模型2：log(λit)=log(Payrollit)+β0

+β1Yearit+bi,0

模型3：log(λit)=log(Payrollit)+β0+bi,0

+bi,1Yearit

模型4：log(λit)=log(Payrollit)+β0

+β1Yearit+bi,0+bi,1Yearit

其中，β0和β1为固定效应，bi,0和bi,1为随机效应。bi,0度量的是第i个风险集合的索赔次数偏离总体均值的程度，bi,0度量的是第i个风险集合的变化率偏离总体平均变化率的程度。假设bi,0和bi,1服从二元正态分布，即bi=(bi,0,bi,1)′～N(0,D)，其方差/协方差矩阵为：

即var(bi,0)=δ0，var(bi,1)=δ1，δ0，1=δ1，0=Cov(bi,0,bi,1)，为信度模型的结构参数。

(二)实证结果

本文利用SAS软件进行实证分析。首先，利用PROC GLMMIX过程步实现的限制性虚拟似然法对信度模型的结构参数进行估计。由于GLIMMIX过程步存在以下三点不足：第一，因变量是事先设定好的，只能选择泊松分布、过离散泊松分布和负二项分布三种；第二，用虚拟数据进行迭代估计，不提供真实似然值，其-2LL只能粗略比较模型优劣；第三，随机效应的标准误存在偏倚，不能用于随机效应显著性检验。因此，本文只用该过程步来确定使用哪个均值方程。经检验最终选择模型3。表1给出模型3的参数估计结果(其他模型估计结果可与作者联系)。

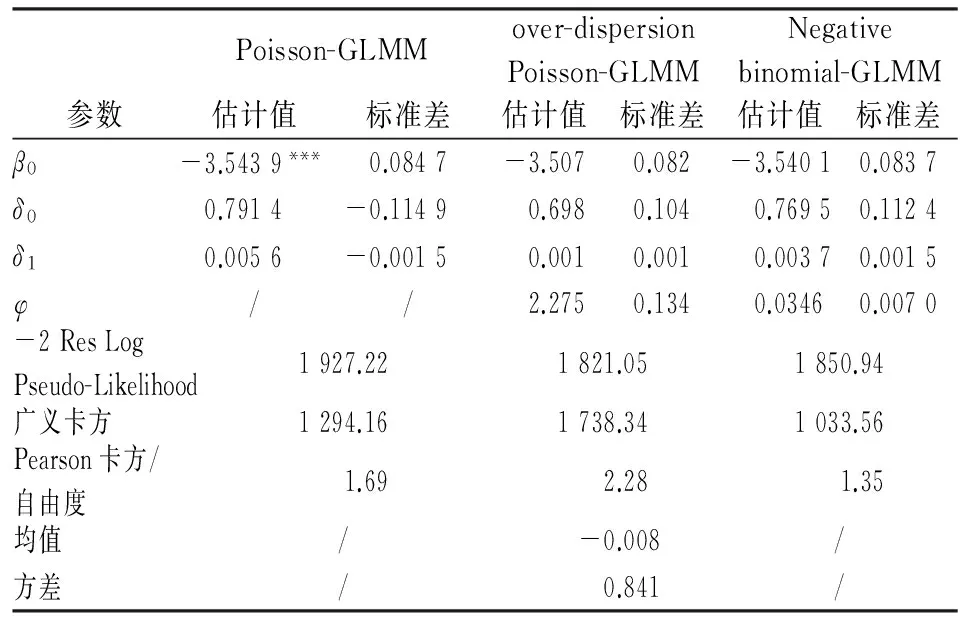
表1 基于限制性虚拟似然法模型3参数估计结果表

表1表明，模型3固定效应的截距项通过显著性检验。SAS PROC GLIMMIX过程步只给出随机效应的估计值和标准误，没有给出随机效应的显著性检验，可以将估计值和标准误的比值近似看成t检验值。在模型3中，泊松广义线性混合模型的随机截距估计值为0.791 4，标准差为-0.114 9，比值为-6.887 7，随机时间估计值为0.005 6，标准差为-0.001 5，比值为-3.733 3；过离散泊松的随机截距比值为6.711 5，随机时间比值为1；负二项的随机截距比值为6.846 1，随机时间比值为2.466 7。一般情况下，t统计量大于2通过显著性检验。因此，模型3随机截距和随机时间很有可能是显著的。下面将会用自适应高斯求积法进一步对参数进行估计。模型拟合部分，由于SAS PROC GLIMMIX过程步参数估计所用数据是用虚拟数据迭代产生的，因此-2 Res Log Pseudo-Likelihood统计量是能粗略判断模型拟合效果，over-dispersion Poisson-GLMM统计量的值最小为1 821.05，说明优于其它两个模型。Pearson卡方/自由度大于1，说明数据存在过离散现象。过离散泊松的Pearson卡方/自由度为2.28，经过调整后为0.841，说明过离散泊松模型对数据的过离散现象有所调整。负二项的Pearson卡方/自由度为1.35大于泊松的1.69，说明负二项模型对过离散也有所调整。

为了克服PROC GLMMIX过程步中的限制性虚拟似然法的三点不足，再使用PROC NLMIXED过程步中的自适应高斯求积法对信度模型结构参数进行估计。该方法的优点是允许因变量分布形式更多；参数估计时所用数据是原始数据，因此其-2LogLikelihood可以用于模型比较；提供了随机效应的显著性检验。表2和表3为用自适应高斯求积法将因变量进一步拓展，对模型3做进一步检验，得到的参数估计结果。

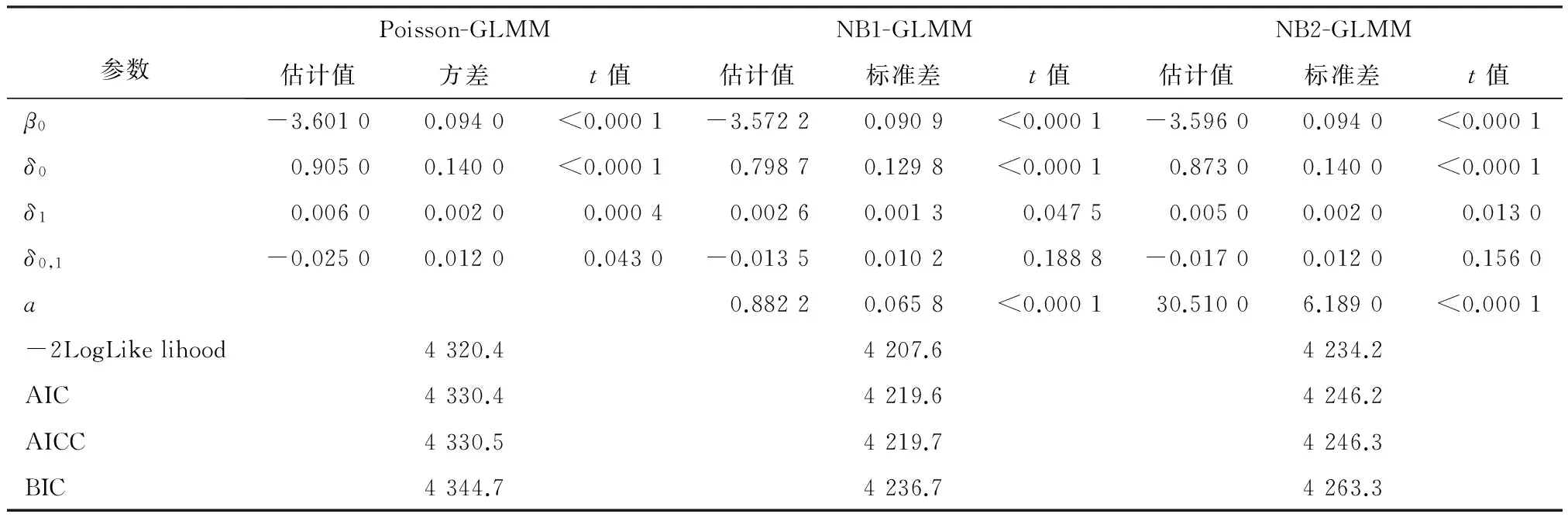
表2 基于自适应高斯求积法模型3参数估计结果表

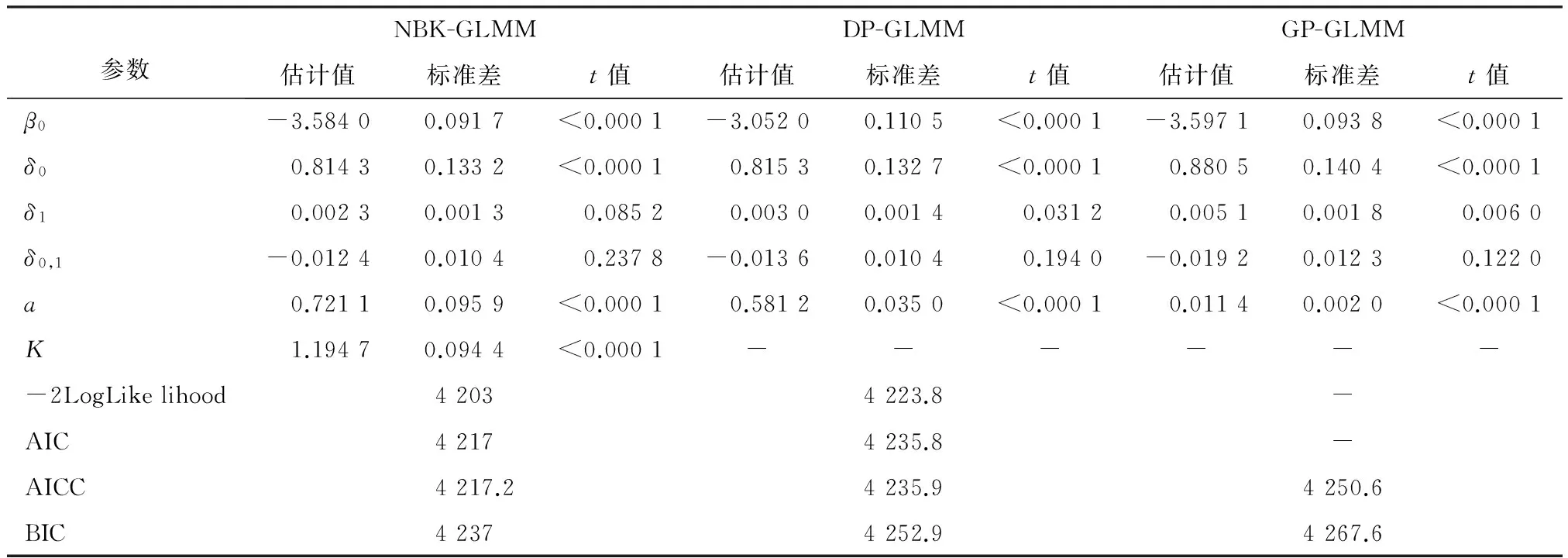
表3 基于自适应高斯求积法模型3参数估计结果表(续)

由表2和表3可知，根据-2LogLikelihood、AIC和BIC越小越优的准则，K=1.194 7负二项K广义线性混合模型对数据的拟合效果最好，其次为负二项1、负二项2、双泊松和广义泊松广义线性混合模型，拟合效果最差的为泊松广义线性混合模型。这进一步说明，当数据存在过离散问题时，泊松广义线性混合模型并不合适，应该采用能处理过离散的广义线性混合模型对数据建模。

四、结 论

本文介绍了信度理论与广义线性混合模型的相关理论及它们之间的关系，并建立了一些拓展的广义线性混合模型，利用这些模型对美国劳工补偿数据进行实证分析，得出以下结论：

第一，在非寿险精算中，由于保险产品的复杂性和多样性，保险产品定价面临较大的不确定性，因此精算师应该采用不同的方法来厘定非寿险产品的费率，比较不同的方法，得出公平准确的最优保费。广义线性混合模型的因变量服从指数分布，该分布族里有很多模型适合非寿险产品定价，能够满足定价多样性的要求。

第二，传统的信度模型虽然是无分布假设，其实际利用方差分析的思想，结构与线性随机效应模型相同，估计结果也相同。线性混合模型，假设因变量服从正态分布，随机效应也服从正态分布。但在精算中，损失数据是离散型数据或者右偏数据，数据的方差也并非常数，因变量与解释变量之间不再是单纯的线性关系。因此，广义线性混合模型弥补了传统定价模型的不足，提高了估计精度，丰富了保险公司费率厘定的工具。

第三，本文对索赔次数建立泊松、负二项1、负二项2、负二项K、广义泊松和双泊松广义线性混合模型。通过检验，发现负二项广义线性混合模型对数据拟合效果最好，其次为双泊松，广义泊松，最后是泊松广义线性混合模型。在负二项广义线性混合模型中，负二项K分布对模型的拟合效果最好，K取值为1.194 7，其次为负二项1分布，最后是负二项2分布。

[1] Frees E W,Young V R，Luo Y.A Longitudinal Data Analysis Interpretation of Credibility Models[J].Insurance：Mathematics and Economics，1999,24(3).

[2] Antonio K，Beirlant J.Actuarial Statistics with Generalized Linear Mixed Models[J].Insurance：Mathematics and Economics，2007,40(1).

[3] Fred K.Generalized Linear Mixed Models for Ratemaking：A Means of Introducing Credibility into a Generalized Linear Model Setting.Casualty Actuarial Society E-Forum[C].Winter.2011.

[4] Ohlsson E，Johansson B.Exact credibility and Tweedie models[J].Astin Bulletin，2006，36(1).

[5] 贺宝龙,唐湘晋.广义线性混合模型在信度理论中的应用[J].金融经济,2008 (10).

[6] 康萌萌.基于广义线性混合模型的经验费率厘定[J]，统计与信息论坛，2009，24(7).

[7] 谢远涛,王稳,谭英平,杨娟.广义线性混合模型框架下的信度模型分析[J].统计与信息论坛,2012,27(10).

[8] 张连增,孙维伟.广义线性混合模型在保险索赔中的应用及R实现[J].江西财经大学学报.2013 (4).

[9] 康萌萌,孟生旺.基于MCMC模拟和伪似然估计法的交叉分类信度模型费率厘定.[J].统计与信息论坛，2014,29(2).

[10] 李政宵，孟生旺.考虑空间效应的贝叶斯分层模型与索赔频率预测[J].数学的实践与认识,2016,46(10).