基于Expectile风险建模的原油价格风险测度研究
胡宗义,万 闯,李 毅
(湖南大学 金融与统计学院,湖南 长沙 410079)
一、引 言
原油作为国际贸易中最活跃的大宗商品之一,其价格的波动是各国政府关注的焦点。特别是进入21世纪以来,围绕原油的博弈日趋激烈。由于国际原油市场受政治、经济等多重因素影响,近年来油价波动呈现出明显的无规则性和不可预测性,而且越来越容易受到突发事件的影响,出现极端市场行为。因此,寻找合理有效的原油价格风险度量方法已刻不容缓。
目前,国际能源领域主流的风险量化手段是风险价值(Value at Risk, VaR)和预期不足(Expected Shortfall,ES)。有关VaR和ES的测算技术有很多,但学术界对哪种技术最优尚未达成共识。这主要是基于以下三个方面的考量:第一,主流的风险测度技术要求假定资产收益分布类型,但问题是收益率分布是时变的,因而会降低结果的可靠性。第二,大多风险建模建立在分位数基础上,但基于分位数的风险度量工具存在严重不足,如不满足次可加性定理,对损失规模不敏感等。尤其对于后者,国际原油市场异常波动,极易出现离群值,采用分位数模型会大大降低油价风险管理质量。第三,对于ES测算工作往往要涉及到复杂函数积分,而且大多数函数的积分不存在闭形式,因而会带来庞大的计算量。因此,基于以上考虑,本文提出采用期望分位数(expectile)方法测算VaR和ES的大小。
期望分位数(expectile)是由Newey等提出[1],与分位数刻画分布的尾部特征类似但不相同。expectile的估计是采用非对称平方损失函数法,它的计算更简洁,估计更有效,而且估计方差和协方差时无需知道条件密度函数。Kuan等证明了基于expectile的VaR对极端损失更加敏感[2];Rossi等证明了其为一致性风险度量工具[3];Taylor推导了expectile与ES之间的数量关系式,可直接用来估计ES,并在实证中取得良好的效果[4]。这奠定了expectile估计ES的理论基础。同时,Kim等指出expectile模型的估计直接采用ALS回归,可跳出对收益分布的假设,避免了模型误设风险[5]。
关于expectile的应用多集中于股指、股票或者基金组合的收益率波动中[4,6-7],极少有文献涉及到大宗商品原油价格风险。原油交易区别于传统的金融资产交易,它同时存在买方和卖方市场,理应有多头和空头之分。Aloui 和Mabrouk 认为油价收益序列的左尾和右尾呈现出显著不同的波动特征[8]。但是,从已有文献来看,仅有陈磊等考察了油价多头和空头水平下的波动特征,获得了VaR估计值[9]。然而,该文并没有考察极端风险水平的油价预测问题,而且无法获得ES估计值,没有解决传统分位数VaR存在的缺陷。为弥补已有文献存在的不足,本文尝试进行三方面的工作:第一,将expectile纳入油价风险研究框架,提出用EAR和CARE模型刻画油价风险,从而挖掘油价波动特征;第二,采用严谨的似然比检验和Bootstrap检验分析模型在不同头寸下的预测效果,并针对极端水平预测效果差的问题,提出采用极值理论与expectile模型相结合的理论方法;第三,从多水平多头寸的角度考察油价收益率,全面地揭示油价收益率的动态演进规律。
二、 原油价格风险测度的模型与方法
expectile又称为期望分位数,与分位数(quantile)类似,它同样可以刻画变量分布的尾部特征。相比于均值回归,它可以更加全面反映自变量对因变量位置、形状等的信息。特别是在风险度量中,expectile对异常值更加敏感。
(一)使用expectile估计VaR和ES
在值风险(VaR)和期望不足(ES)已经发展成为现代金融风险管理中两大标准的风险度量工具。对VaR建模的方法有很多,其中绝大多数都是基于分位数的思想,存在诸多不足。Kuan等提出使用expectile估计VaR,可以有效改善分位数VaR的不足[2]。令Y为某一资产组合收益率的随机变量,其分布为FY,Y的第τ个expectile值为:
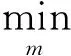
(1)
其中,τ∈(0,1)在风险度量中称为谨慎性水平,当τ=0.5时,expectile退化成变量的均值。Qτ(x)=|τ-I(x<0)|x2表示非对称平方损失函数。μ(τ)为第τ个expectile 的估计值,也是VaR的估计值。Taylor等证明了μ(τ)的大小取决于随机变量的尾部期望规模[4],即:
=μ(τ)-E(Y)
(2)
式(2)实际上给出了expectile与ES之间的关系。ES定义为超出VaR部分的条件损失均值,即ES(τ)=E[Y|Y<μ(τ)]。将式(2)化简成尾部期望形式:
E[Y|Y<μ(τ)]=
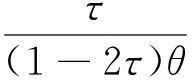
(3)
其中,θ为样本落在μ(τ)下方的比例。式(3)给出了θ<0.5时的数量关系式,对于上尾部(θ>0.5)的风险测度工作,只需将τ和θ分别替换成1-τ和1-θ即可。Efron证明了expectile与分位数之间存在一一对应的关系[10],即存在分位数估计值q(θ),q(θ)=μ(τ)。至此,本文给出了基于expectile建立的VaR和ES之间的联系。
(二)基于expectile的原油价格风险测度模型
本文基于expectile度量技术,构建如下风险测度模型:
Yt=ft,τ(β)+εt,τ,0<τ<1
(4)
其中,Yt为油价收益率,τ为给定的谨慎性水平。ft,τ(β)是由β∈Rp构造的平稳过程,它的估计即为Yt的第τ个expectile值,也是VaR的估计值。εt,τ为τ水平下的随机扰动项,满足μεt(τ)=0,本文对其分布形式不做任何假定。通过设定ft,τ(β)的形式,可以刻画不同特点的风险演进规律,其中最主要的是EAR模型和CARE模型。
EAR(Expectile Auto Regression)模型是刻画收益率序列变化的回归模型之一,该模型认为过去的收益率会影响当前收益率,其模型形式为:
(5)
其中,q为滞后阶数,它的大小根据相关准则如AIC准则确定。Kuan等证明了该模型的渐进正态分布性质[2]。EAR模型优缺点十分明显,主要在于模型构造简单,对参数不施加任何约束,但它仅仅考虑过去收益率的动态演进形式,忽视了风险影响的持续性,因此不能平滑地刻画风险变化过程。后来,Taylor等提出了条件自回归expectile(CARE)模型,可以同时考察收益率和VaR影响的持续性[4]。
CARE模型与Engle等提出的CAViaR模型的建模思想相同[11]。Engle认为VaR作为资产组合收益序列的某一尾部特征值,也应存在具有金融时间序列的典型特征,因而可以直接对VaR进行自回归建模,跳出对收益分布的假设。CARE模型对expectile进行自回归建模,其模型形式为:
(6)
其中,∑βi+1ft-i,τ(β)为expectile的自回归项,用来反映风险影响的持续性;∑βp+j+1l(yt-j)为市场冲击项,体现了收益率的滞后观测值对风险的影响。为了考察正负收益率对风险的不对称影响,Engle提出了AS模型形式,其形式为:
ft,τ(β)=β0+β1ft-1,τ(β)+β2yt-1I(yt-1≥0)+
β3yt-1I(yt-1<0)
(7)
该模型考察了市场信息的非对称效应,在实际应用中应用最广泛,如简志宏、彭伟等人的研究[12-13]。Kim等进一步完善了CARE模型的相合性与渐进正态分布性质[5]。
expectile模型的求解采用的是Aigner等提出的非对称最小二乘回归(ALS),即:
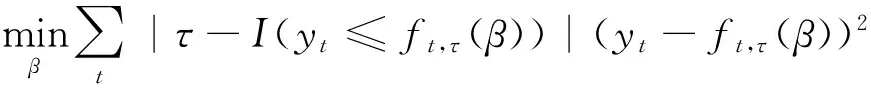
(8)
通过设置不同的τ,可以充分刻画油价收益率在不同谨慎性水平下的位置、刻度和波动特征。
(三)极端风险度量方法改进:expectile-EVT模型
为考虑极端水平对原油价格风险的影响,本文将极值理论引入到expectile模型,构建expectile-EVT模型。该模型结合expectile处理常规水平VaR的稳健性,以及极值理论在拟合尾部风险的有效性,因而该模型在理论上度量极端油价风险时具有一定优势。以多头头寸为例,将expectile与EVT相结合的方法如下。
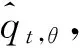
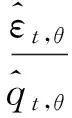
(9)
其次,令p(p<θ)为所求的极端风险水平,它与式(9)中标准化残差序列的关系满足:
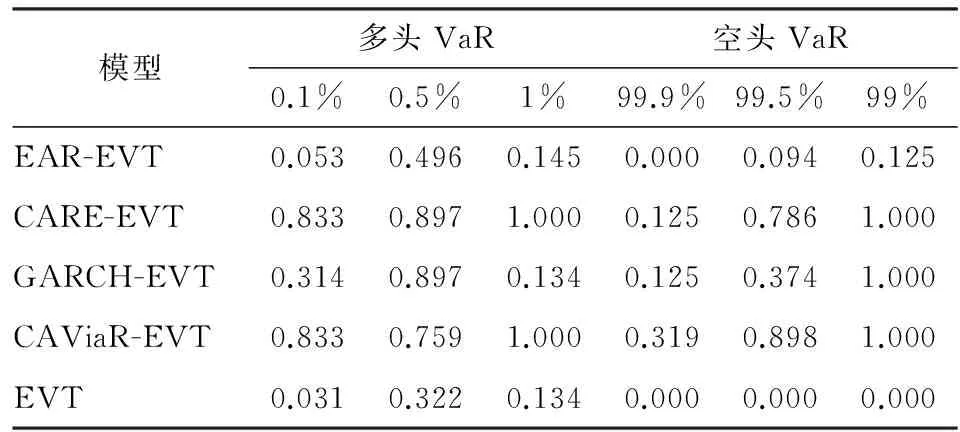
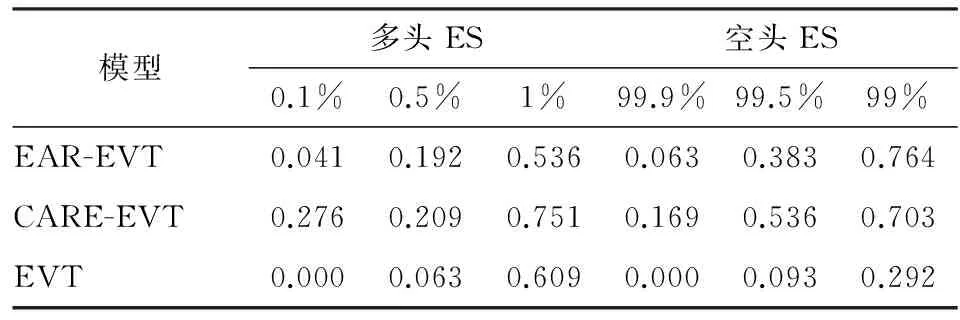
Pr(rt (10) 其中,qt,θ为负值,可以由expectile模型估计得到。zp=qt,p/qt,θ-1为标准化残差序列的1-p分位估计值,可以由EVT方法求解。 从上述建模过程可以发现,expectile与EVT的结合实际上是将所求的极端水平p的风险值转化成求解标准化残差序列的1-p分位估计值。因此,建模的关键在于采用EVT对zp进行求解。常用的EVT求解方法有两种:分组极大值模型(BMM)和超阈值模型(POT)。本文采用POT模型建模,因为该模型可以有效利用超过阀值的观测信息,对数据量要求较少,而且对突发事件有较强的预见性。另一方面,POT模型目前已广泛用于极端风险管理实务中,在实证中取得较好效果。有关POT模型求解过程参见McNeil等的研究[14],本文限于篇幅不做详细介绍。 本文的研究对象为西德克萨斯中质原油(WTI)。WTI原油是世界三大基准油之一,其现货产品在纽约商品交易所(NYMEX)挂牌交易,至今已有近40年的历史。依托纽交所商品交易良好的流通性和价格透明度,WTI原油价格被国际上视为主要的定价基准。考虑到每个交易日受到当前市场信息的影响,本文将每日结算价作为实证样本,数据来源于美国能源情报署。 近年来,受国际政治、经济因素的影响,国际原油市场变得愈发不稳,油价风险管理迫在眉睫。因此,本文将2001年1月2日定为样本的初始日期,将可获得的最晚日期2017年7月4日确定为样本的终止日期,样本规模为4 019个。其中前3 019个数据作为估计样本,后1 000个数据作为预测样本。油价收益率计算采用的形式为: rt=100×(lnpt-lnpt-1),t=1,2,…,T (11) 其中pt为第t交易日的结算价格。表1给出了研究数据的描述性统计信息。 表1 WTI油价收益率序列的描述性统计量 注:J-B为Jarque-Bera统计量p值;ADF为Augmented Dickey-Filler单位根检验统计量p值;***代表1%显著性水平下显著。 由表1可以看出:WTI油价收益序列具有明显左偏(偏度)和高峰厚尾(峰度)形态;JB和BDS检验的p值都在99%显著性水平下拒绝原假设,表明WTI和美元指数收益率序列均拒绝正态分布和独立同分布假设,ADF 检验表明收益率序列是平稳的,可以进行建模。 由于国际原油市场采取双向交易模式,即同时存在买方市场和卖方市场。现有的文献大多选择度量下侧风险(如1%和5%),但原油市场具有多头和空头之分,原油价格的涨跌会对相关头寸的持有者造成损失。因此,本文同时考察多头和空头VaR的波动特征,其中选择0.5%、1%、5%和10%的expectile作为油价下侧风险水平,表明原油期货多头持有者面临的风险,简记为多头VaR;而选择99.5%、99%、95%和90%的expectile值作为空头持有者面临的风险,简记为空头VaR。 表2给出了EAR模型在不同水平下的最优滞后阶数以及一阶滞后项的系数估计值。表2中所有谨慎性水平下EAR模型的最优滞后项数目都大于等于9,这说明油价收益率序列具有典型的长记忆性特征。事实上,本文在对油价收益率序列做Ljung-Box检验时,发现Q(10)统计量显著拒绝原假设,这也证实了油价收益率具有明显的长记忆性。此外,一阶滞后系数均高度显著,即油价收益率是序列相关的,并且前一期收益率对当期油价风险的影响随着谨慎性水平的变化而变化。进一步观察可以发现:油价收益率对下尾VaR产生负向影响,而对上尾VaR具有明显正向影响。特别是在多头情形下,随着谨慎性水平的减小,前期的市场冲击项对当前VaR的冲击效果越明显。 表2 EAR模型估计结果 注:***、**分别表示1%、5%显著性水平。滞后项数目由相关信息准则确定。 表3 多头CARE模型估计结果 注:***、**、*分别表示1%、5%和10%显著性水平;β1为常数项系数;β2为自回归项系数,反映了滞后一期风险项的影响,β3和β4反映了前期正负收益率对当期油价风险的冲击。下表同。 表3、表4分别给出了CARE模型在多头和空头VaR下的模型估计结果,包括系数估计值、标准差以及显著性检验统计量p值。综合分析表3和表4,可以得出以下结论:(1)所有谨慎性水平下模型的自回归系数β2均高度显著。这表明油价VaR波动序列存在典型的自相关特征,即当前风险值与过往风险规模高度相关。(2)在多头头寸下,系数β3和β4在绝大多数情形下均高度显著。油价的上涨和下跌会同时影响多头风险的大小,并且随着谨慎性水平不断减小,油价风险受正负市场冲击项的影响不断加重。(3)在空头头寸下,从表4可以发现,市场冲击项中仅有β4在任何水平下高度显著。这表明空头风险主要受油价下跌的影响,而且随着空头水平的增加,油价下跌对风险的影响面不断加大。这暗示相关头寸持有者,在分析下侧风险时应同时注意油价涨跌的影响,而在上侧风险测度中应特别关注油价的下跌效应。(4)分析表3和表4结果,不难发现在越极端的谨慎性水平(如0.5%、1%、99.5%和99%)下,油价收益率对当前风险的冲击越大。另外,空头和多头头寸CARE模型的市场冲击系数β3和β4的正负号相反,这说明油价的上涨和下跌对多头和空头风险产生反向影响。 表4 空头CARE模型估计结果 1.VaR和ES后验检验方法说明。为了检验上述模型在不同水平下得到的动态VaR的预测精度,Kupiec构造了一种似然比检验统计量,将其命名为无条件覆盖(Unconditional Coverag)检验[15]。该检验首先计算VaR的“碰撞序列”Hitt,满足: (12) 它表示,若yt+VaRt<0,意味着这是一次失败事件,称之为击中(Hit)事件。如果模型可以很好地反映油价风险的波动,那么碰撞序列应该服从贝努利分布。此时,可以构造似然比检验统计量: LRuc= (13) 其中,θ为所有失败事件的比例,K为超出VaR部分的观测值个数,N为总的观测序列的规模。当LR统计量落入卡方分布临界值的右边时,即p值小于给定的显著性水平时,拒绝原模型。反之,则接受原模型。 (14) (15) (16) Pvalue (17) 2.模型后验结果分析。在不同谨慎性水平下得到CARE模型和EAR模型的参数估计值,将其重新代入模型便得到动态VaR的估计序列。根据式(4),可由动态VaR估计序列得到动态ES估计序列。利用VaR和ES的后验检验对expectile模型进行诊断,所得检验统计量的p值见表5。 表5 模型后验检验结果 注:表中数据为VaR和ES检验统计量p值,p值越大,模型预测精度越高。 从表5中VaR和ES后验检验结果可以发现,在常规风险水平下(如5%、10%和95%、90%),CARE和EAR模型均能通过似然比检验和Bootstrap检验。这说明本文中两类expectile模型均能很好地刻画油价风险的动力学特征。但是在极端风险水平下如(0.5%,1%等),仅有CARE模型部分通过5%显著性水平的后侧检验。这是因为在极端水平下,半参数CARE模型在模型优化时采用非对称平方损失函数,非对称程度越高,模型可利用的数据信息极少,因此会造成模型估计结果的不稳定性和不适用性。针对该问题,本文考虑采用与极值理论相结合的方法进行改进。最后,从表5所做的16次对比中,CARE模型后验检验p值大于EAR模型的p值的次数有14次,这说明CARE模型相比于EAR模型具有更优的风险预测精度。 3.极端风险后验结果分析。引入极值理论控制极端水平对原油价格风险预测的干扰,同时为进行比较研究,本文采用expetile-EVT模型、GARCH-EVT模型、EVT模型以及CAViaR-EVT模型对原油价格风险进行测度。表6和表7报告了各个模型在极端风险水平0.1%、0.5%和1%以及对应的空头头寸99.9%、99.5%和99%水平下的后验检验结果。可以得到如下结论:(1)将极值理论引入到expectile模型中可以显著提高模型在极端水平下的预测精度,由表6、表7可以发现,除了99.9%的显著性水平下,EAR-EVT模型没有通过似然比检验统计量,其余无论是VaR还是ES均通过5%显著性水平的假设检验;(2)就VaR而言,CARE-EVT、GARCH-EVT以及CAViaR-EVT均通过似然比检验统计量,这说明3个模型均可以用于预测VaR。但3个模型在6种水平下达到最优的次数分别为4,2,5次,意味着相较于另外两个模型,GARCH-EVT模型的效果要弱一点。究其原因,GARCH模型需要选择合适的波动率分布类型,这往往会带来模型选择误差,降低预测精度。而CAViaR和CARE模型则不需要面对这个问题。EVT模型的预测效果最差,特别是在空头风险水平下,其检验统计量p值甚至为0。EAR-EVT模型的效果也弱于剩下3个模型效果,这是因为与GARCH、CARE与CAViaR模型相比,EAR模型的建模没有引入风险的自回归项。因此当油价市场出现异常波动时,EAR模型在反应风险时会出现滞后现象;(3)尽管EVT模型也可以作为ES估计的手段之一,但CARE-EVT和EAR-EVT模型检验结果均要优于EVT模型。因此,在实际应用中,不推荐使用EVT模型。总体而言,本文提出的expectile-EVT模型尽管在极端水平的VaR预测中并无太大优势,但它可以迅速获得极端水平下的ES估计值,并且可以通过ES后验检验,因而可以更加准确地分析油价市场风险可能发生的极端事件带来的冲击,以便相关头寸的持有者快速有效地做出管控措施。 表6 极端风险下VaR后验分析结果 注:表中数据为VaR统计量的p值,p值越大,模型预测精度越高。 表7 极端风险下ES后验分析结果 注:表中数据为ES检验统计量的p值,p值越大,模型预测精度越高。 原油作为国际上最活跃的大宗商品之一,其价格风险的测度和防范工作始终是能源领域研究的热点之一。本文以WTI现货原油价格为例,采用半参数expectile模型中的EAR和CARE模型对油价变化的动力学特征进行了深入考察。运用严谨的似然比检验和Bootstrap检验方法对比了两种模型在多头和空头两种头寸下的预测精度,并针对极端风险预测效果不佳的问题,将极值理论引入到expcetile模型中。通过实证研究得出以下结论: 第一,油价收益率序列呈现典型的长记忆性和自相关性特征,并受往期收益率的不对称影响,且在空头和多头头寸下呈现出不同的波动特征:在多头头寸下,油价上涨和下跌会同时影响风险规模,且下跌的反响更强烈;而在空头头寸下,风险规模仅受油价下跌的影响。 第二,通过VaR和ES的后验检验发现expectile模型对常规水平风险具有较强的预测能力,并且CARE模型要优于EAR模型。但是在极端风险水平下,两类模型仍需改进。 第三,为了预测极端水平下VaR和ES,本文将极值理论巧妙地与expectile模型结合,构建expectile-EVT模型,结果发现极值理论可以有效提高expectile模型预测绩效,并且在ES风险度量中更具优势。 总之,本研究首次将expectile工具应用到油价风险度量中,揭示了油价风险变化的典型特征。从风险管理角度来看,这些可以为中国应对国际原油市场价格风险提供良好的理论指导,进而丰富风险测度方法的选择。 [1] Newey W K,Powell J L.Asymmetric Least Squares Estimation and Testing[J].Econometrica:Journal of the Econometric Society,1987(4). [2] Kuan C M,Yeh J H,Hsu Y C.Assessing Value at Risk with CARE,the Conditional Autoregressive Expected Shortfall Models[J].Journal of Econometrics,2009(2). [3] Rossi G,Harvey A.Quantiles,Expectiles and Splines[J].Journal of Econometrics,2009(2) [4] Taylor J W.Estimating Value at Risk and Expected Shortfall Using Expectiles[J].Journal of Financial Econometrics,2008,6(2). [5] Kim M,Lee S.Nonlinear Expectile Regression with Application to Value-at-Risk and Expected Shortfall Estimation[J].Computational Statistics & Data Analysis,2016,94(2). [6] 苏辛,周勇.条件自回归expectile模型及其在基金业绩评价中的应用[J].中国管理科学,2013(21). [7] 谢尚宇,姚宏伟,周勇.基于ARCH-Expectile方法的VaR和ES尾部风险测量[J].中国管理科学,2014(9). [8] Aloui C,Mabrouk S.Value-at-risk Estimations of Energy Commodities Via Long-memory,Asymmetry and Fat-tailed GARCH Models[J].Energy Policy,2010,38(5). [9] 陈磊,曾勇,杜化宇.石油期货收益率的分位数建模及其影响因素研究[J].中国管理科学,2012(3). [10] Efron B.Regression Percentiles Using Asymmetric Squared Error Loss[J].Statistica Sinica,1991(1). [11] Engle R F,Manganelli S.CAViaR:Conditional Autoregressive Value at Risk by Regression Quantiles[J].Journal of Business & Economic Statistics,2004,22(4). [12] 简志宏,曾裕峰,刘曦腾.基于CAViaR模型的沪深300股指期货隔夜风险研究[J].中国管理科学,2016(9). [13] 彭伟,曾裕峰,袁阳阳.基于门限加权不对称斜率模型的CAViaR研究[J].系统管理学报,2016(3). [14] McNeil A J,Frey R.Estimation of Tail-related Risk Measures for Heteroscedastic Financial Time Series:An Extreme Value Approach[J].Journal of Empirical Finance,2000,7(3). [15] Kupiec P H.Techniques for Verifying the Accuracy of Risk Measurement Models[J].The Journal of Derivatives,1995,3(2).
三、原油价格风险测度的实证分析
(一)数据来源及预处理

(二)国际原油价格风险的测度

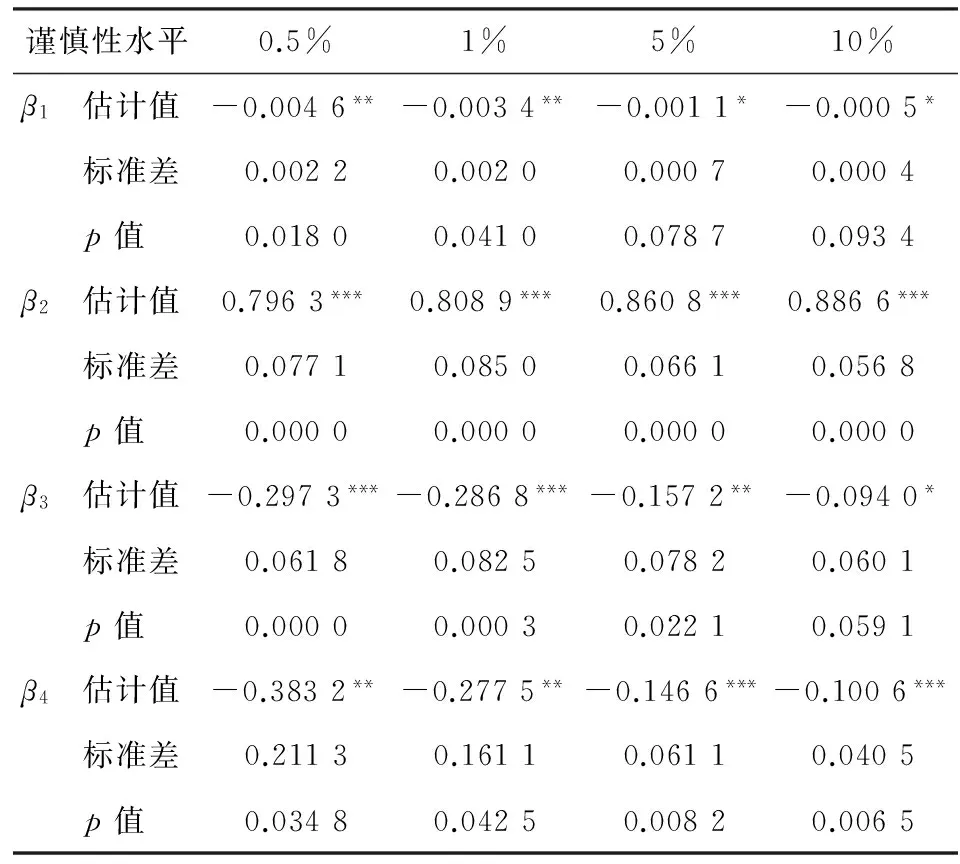
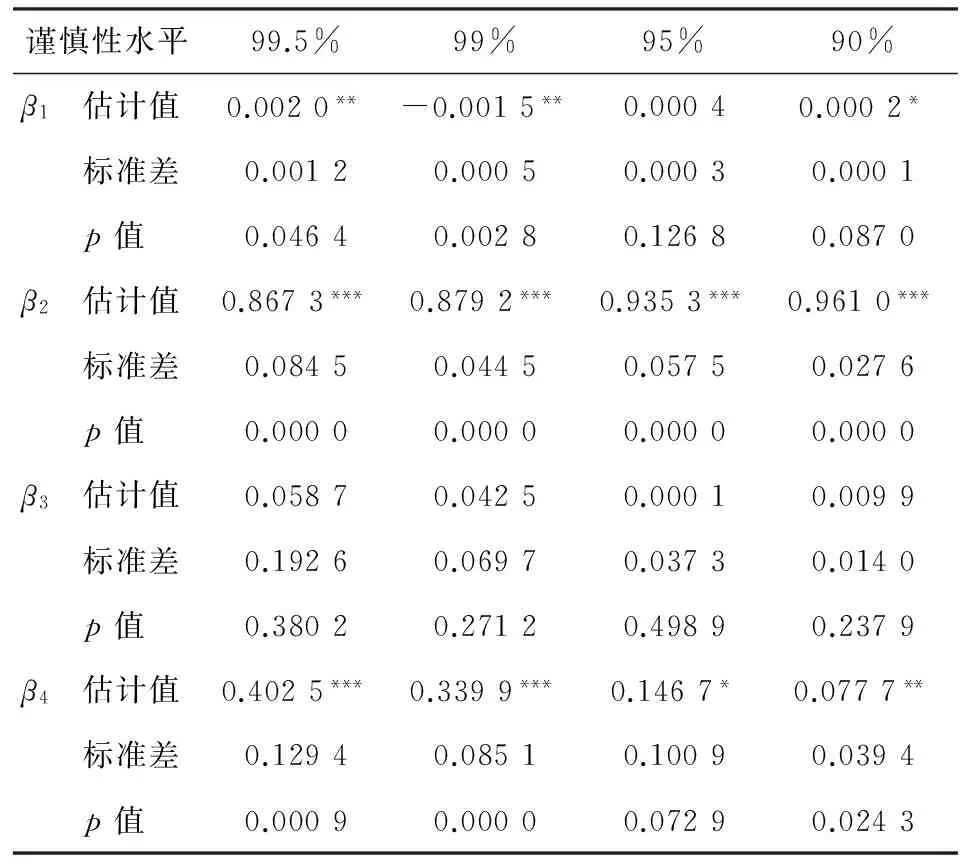
(三)后验分析
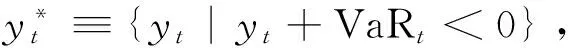
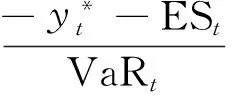
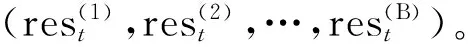
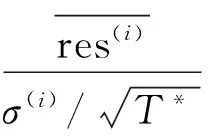
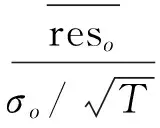
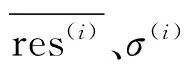

四、 结 论

