基于粒度的电子系统环节及传递关系模型的确定方法*

罗天峰，易 瑔，曹 勇

（陆军装甲兵学院，北京 100072）

0 引言

半实物仿真是在计算机仿真回路中接入一些实物进行试验，取代相应的数学模型，这样更接近实物，获取信息更准确［1］。半实物仿真设计主要根据原有系统的某种属性建立仿真模型，其重点关注系统作用的实现。曹勇等人提出的环节及传递关系建模方法，为复杂系统的半实物仿真设计提供了一种可行性方法［2-3］。

但仅仅为半实物仿真设计提供基本模型还不够，仍存在以下问题：一是仿真模型的分辨率是否满足仿真任务的需求；二是仿真模型中的部分环节能否进行工程实物化，即是否易于工程实现；三是建立的实物模型能否易于检测，从而获取实验信息。

为解决上述问题，本文在环节及传递关系模型研究基础上，引入了粒度的概念。粒度是对问题的不同角度、不对层次进行细化的度量［4］。1979年Zadeh在文献中提出并讨论了模糊信息粒度。本文采用粒度作为评价环节及传递关系的指标，确定电子系统的环节及传递关系模型，以满足仿真任务的不同层次及分辨率要求，提高了其工程适应性。

1 基于粒度的环节及传递关系模型

环节及传递关系模型是选取全系统功能作为数据域，按照系统功能划分域，在系统功能域构成的解空间内，构建基于功能域的信息流传播模型。在确立功能域的基础上，按照环节的形式划分系统的内部事件，以功能相关的独立结构作为一个环节，将映射作为运算置于环节中，每个环节独立构建输入输出映射模型，并将环节按照信号的传递关系连接起来，特定功能由一系列相关环节级联而成。环节及传递关系模型在建模过程中关注系统功能空间的维数、信号的接口属性、映射作用及功能环节间的传递关系。环节及传递关系模型如图1所示。

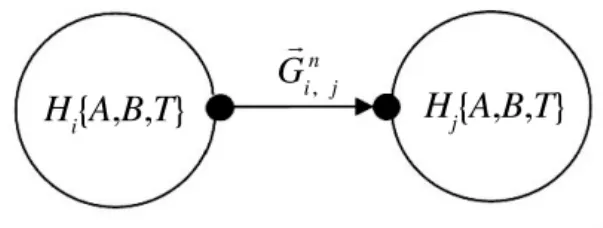
图1 环节及传递关系模型

电子系统环节及传递关系模型在某种属性下，经过聚合后，使模型结构得到简化，仿真设计简化，但仿真建模的分辨率下降；在某种属性下，经过解聚后，仿真建模的分辨率提高，但模型结构变得复杂，仿真设计工作量增加。因此，如何评价环节及传递关系模型是否合理，从而建立恰当的仿真模型是一项重要技术，而粒度为确定电子系统环节及传递关系模型的结构提供了一种有效手段。

环节及传递关系模型中的不同环节可以看作是一个个不连续的信息颗粒，每个信息颗粒具备的信息量是不同的。因此，通过描述每个环节的粒度，可以恰当地反映该环节的某种属性。本文将环节的粒度定义为级别、单一性和透明性3个属性。其中，粒度的级别描述的是信息粒的粗细，粒度级别越高，信息粒越粗，模型分辨率越低，反之则模型分辨率越高；粒度的单一性和透明性则描述环节的输入输出特性，环节的粒度具备单一性，则该环节所有输出信号均相关，环节的粒度具备透明性，则该环节所有输入信号均相关。通过引入粒度这一概念，可以反映出环节及传递关系模型的分辨率和各环节的输入输出特性。

2 模型的确定方法及步骤

确定电子系统环节及传递关系模型的基本方法如下：将模型按照功能域划分为若干相关环节及传递关系，采用粒度作为评价环节及传递关系的指标，通过粒度的级别、单一性和透明性3个基本特性规划和修正该模型，从而实现确定电子系统环节及传递关系模型的目的。具体步骤如下：

2.1 确定环节及传递关系模型粒度的级别、单一性和透明性

2.1.1 确定环节及传递关系模型粒度的级别

如果在系统的功能域 F={f1，f2，…，fn}中，环节 Hx对应的独立功能fx∈F，可以拆分成n个独立功能fx1，fx2，…，fxn∈F，且独立功能 fx1，fx2，…，fxn对应的 n个新环节Hx1，Hx2，…，Hxn间具有串联或并联相关性，则环节Hx可以解聚为多个子环节Hx1，Hx2，…，Hxn，即：

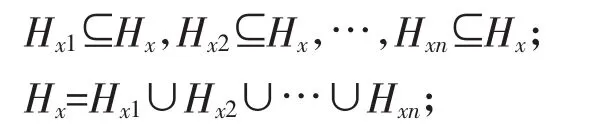
则子环节Hx1，Hx2，…，Hxn的粒度级别小于原环节Hx的粒度级别。

粒度级别体现了仿真模型的粗细程度。模型经过聚合后，模型的复杂程度降低，但粒度变粗，粒度级别升高，模型的分辨率下降；模型经过解聚后，模型的复杂程度增加，但粒度变细，粒度级别下降，模型的分辨率得以提升。因此，粒度级别的确定，为模型分辨率的评价提供了定性依据。

2.1.2 确定环节及传递关系模型粒度的单一性

在环节H{A，B，T}中，若输出信号集B中的元素bi之间具备相关性，则该环节的粒度具备单一性。否则，该环节的粒度不单一。

粒度的单一性表征了环节输出信号B中元素之间的相关性，其特征为：当环节为单一粒度时，其输出信号为相关信号集，即输出信号类型保持一致。不难看出，单一粒度的模型较不单一粒度的模型更加适于建模仿真的工程实现。

2.1.3 确定环节及传递关系模型粒度的透明性

在环节H{A，B，T}中，若输入信号集A中的元素ai之间具备相关性，则该环节的粒度具备透明性。否则，该环节的粒度不透明。

粒度的透明性强调了环节输入信号A元素之间的相关性，其特征为：当环节为透明粒度时，其输入信号为相关信号集，即输入信号类型一致。可以看出，透明粒度的模型较不透明粒度的模型更加易于工程检测。

2.2 通过粒度的级别，规划环节及传递关系模型的结构

电子系统环节及传递关系模型的功能域F={f1，f2，…，fn}中，环节 Hx对应的独立功能 fx∈F。当环节Hx的粒度级别高于仿真任务的分辨率需求时，且环节 Hx可以拆分成 n 个独立功能 fx1，fx2，…，fxn∈F，独立功能 fx1，fx2，…，fxn对应的 n 个新环节 Hx1，Hx2，…，Hxn间具有串联或并联相关性，则环节Hx解聚为多个子环节 Hx1，Hx2，…，Hxn；当环节 Hx的粒度级别低于仿真任务的分辨率需求时，且n个环节H1，H2，…，Hn间具有串联或并联相关性，则n个环节H1，H2，…，Hn聚合为一个新环节Hn+1，Hn+1对应的独立功能 fn+1∈F。

通过对环节Hx的粒度级别与仿真任务分辨率需求相比较，可评价该模型结构是否满足任务需求，并通过对不满足任务分辨率需求的环节Hx进行聚合和解聚，使其产生的新环节满足分辨率需求，从而实现对电子系统环节及传递关系模型结构的规划。

2.3 通过粒度的单一性，修正环节及传递关系模型，优化模型的工程可实现性

在环节Hx{A，B，T}中，该环节的粒度不单一，输出信号集B中的元素bi之间不具备相关性，若该环节 Hx可以拆分成n个独立功能 fx1，fx2，…，fxn∈F，独立功能 fx1，fx2，…，fxn对应的 n 个新环节 Hx1，Hx2，…，Hxn间具有串联或并联相关性，则环节Hx解聚为多个子环节 Hx1，Hx2，…，Hxn，每个子环节的粒度具有单一性，其输出信号为相关信号集，即输出信号类型保持一致，则这些子环节可工程实现。

2.4 通过粒度的透明性，修正环节及传递关系模型，优化模型用于工程检测的适应性

在环节Hx{A，B，T}中，该环节的粒度不透明，输入信号集A中的元素ai之间不具备相关性，若环节Hx 可以拆分成 n 个独立功能 fx1，fx2，…，fxn∈F，独立功能 fx1，fx2，…，fxn对应的 n 个新环节 Hx1，Hx2，…，Hxn间具有串联或并联相关性，则环节Hx解聚为多个子环节Hx1，Hx2，…，Hxn，每个子环节的粒度具有透明性，其输入信号为相关信号集，即输入信号类型一致，则这些子环节易于工程检测。

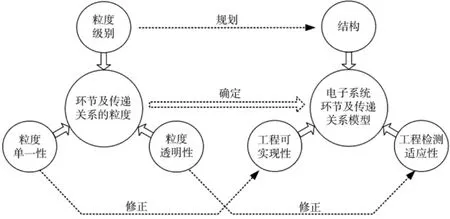
图2 确定电子系统环节及传递关系模型的步骤

3 实例建模

下面以一个实际电路为例，说明本文提出的方法步骤。

图3所示为火控计算机D/A转换电路（DAC1230芯片）内部逻辑关系，DAC1230为输入锁存12位D/A转换器，是一个模/数混合芯片，内部有一个T型电阻网络，用以实现D/A转换，其输出为电流信号，需要外接运算放大电路，得到模拟电压输出。

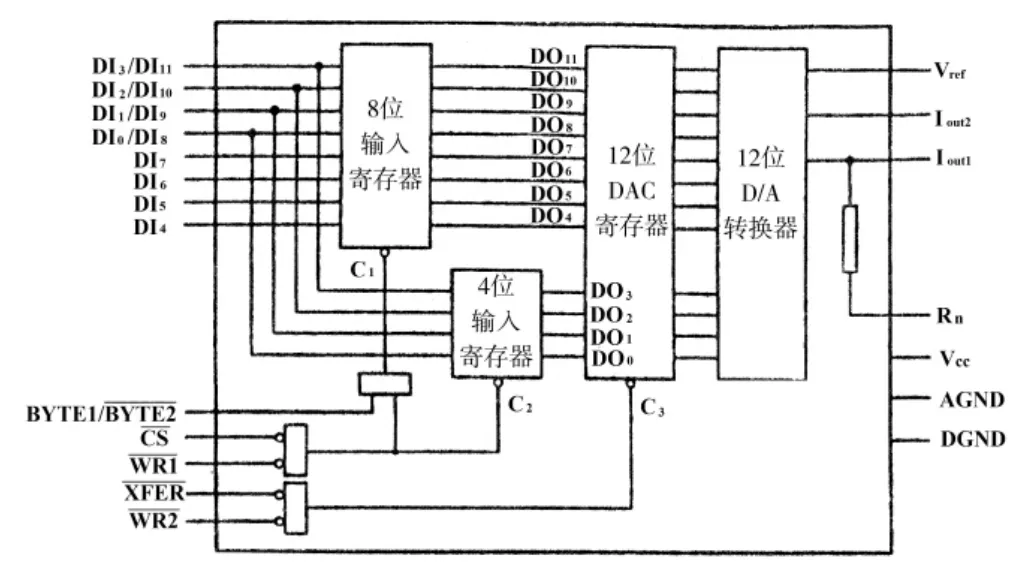
图3 12位D/A转换器DAC1230的电路原理图

其环节及传递关系模型如图4所示。

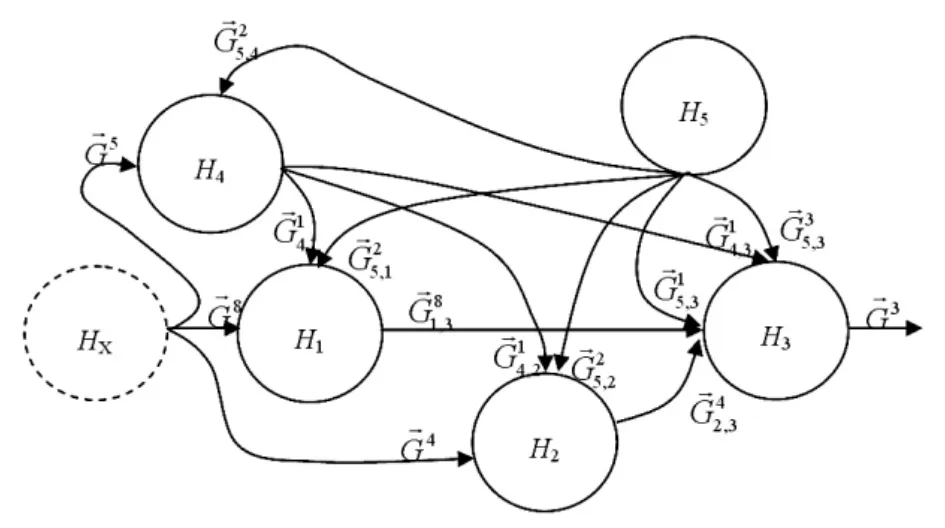
图4 12位D/A转换器DAC1230对应的环节及传递关系模型

通过粒度的3个基本特性，确定DAC1230芯片环节及传递关系模型的步骤如下所示。

3.1 通过粒度的级别，规划DAC1230芯片环节及传递关系模型的结构

如图4所示模型中，与图3电路原理图对应，其各个环节分别为：

①H1：等效于8位输入寄存器的单向可控环节；

②H2：等效于4位输入寄存器的单向可控环节；

③H3：等效于12位寄存D/A转换器的单向可控环节；

④H4：等效于控制信号组合逻辑的单向可控环节；

⑤H5：等效于供电的源环节；

⑥HX：为外部某个相关环节，不属于本模型。

3.1.1 DAC1230芯片仿真模型要求精确到元件层次

环节H3是由12位DAC寄存器和12位D/A转换器两个电路单元共同构成的，该环节粒度级别高于仿真任务的分辨率需求，将12位DAC寄存器构建为环节H31，12位D/A转换器构建为环节H32，则环节H31及环节H32具有串联相关性，可以将环节H3解聚为H31、H32两个新的环节，如下页图5所示。解聚后两个环节均等效于单个元件，其粒度级别满足仿真任务的分辨率需求。

环节H4是一个组合逻辑，是由12位输入寄存控制逻辑和12位DAC寄存控制逻辑共同构成的，该环节粒度级别高于仿真任务的分辨率需求，将12位输入寄存控制逻辑构建为环节H41，12位DAC寄存控制逻辑构建为环节H42，则环节H41和环节H42具有串联相关性，可以将环节H4解聚为H41、H42两个新的环节，如图5所示。解聚后的两个环节均等效于单个元件控制逻辑，其粒度级别满足仿真任务的分辨率需求。

经过解聚后的模型粒度级别均满足仿真任务需求，据此实现对DAC1230芯片仿真模型结构的规划。

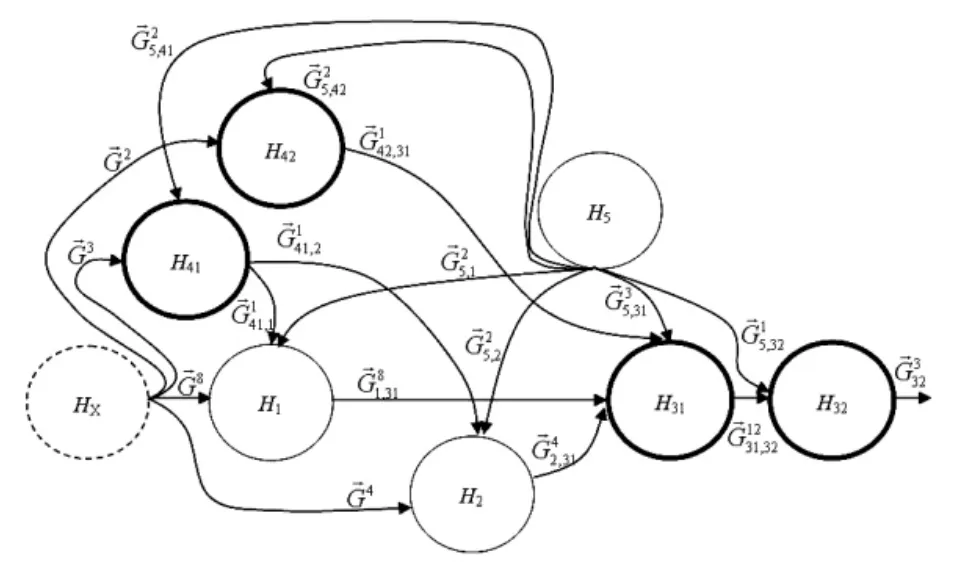
图5 第1种规划的环节及传递关系模型

3.1.2 DAC1230芯片仿真模型要求精确到基本功能层次

如图4中，环节H1等效于8位输入寄存器的单向可控环节，H2等效于4位输入寄存器的单向可控环节，两个环节具有相同的输入寄存器功能，环节H1和H2的粒度级别低于仿真任务的分辨率需求，在输入寄存器功能限定下，H1，H2两个环节具有并联相关性，可以将H1，H2两个环节聚合为一个新的环节H6，如图6所示。聚合后的环节粒度级别满足仿真任务的分辨率需求，据此实现对DAC1230芯片仿真模型结构的规划。

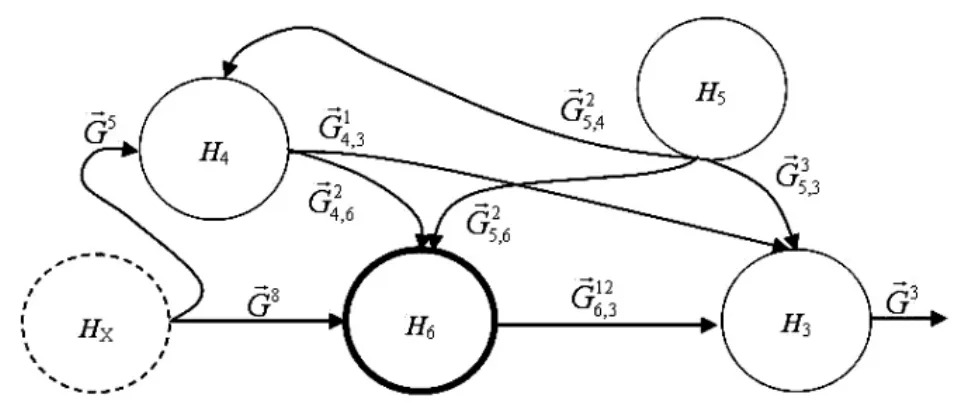
图6 第2种规划的环节及传递关系模型

3.2 通过粒度的单一性，修正DAC1230芯片环节及传递关系模型，优化模型的工程可实现性

如图4所示模型中，与图3电路原理图对应，其环节输出信号B如表1所示。

由表1可知，由于环节H3粒度不单一，该环节难以工程实现，因此，将环节H3解聚为环节H31和环节H32，其中环节H31输出信号为2维，等效于信号IOUT1、IOUT2，环节H32输出信号为1维，等效于信号Rn，则环节H31及环节H32具有并联相关性，如图7所示。解聚后两个子环节的粒度具有单一性，其输出信号为相关信号集，则这两个子环节可工程实现。

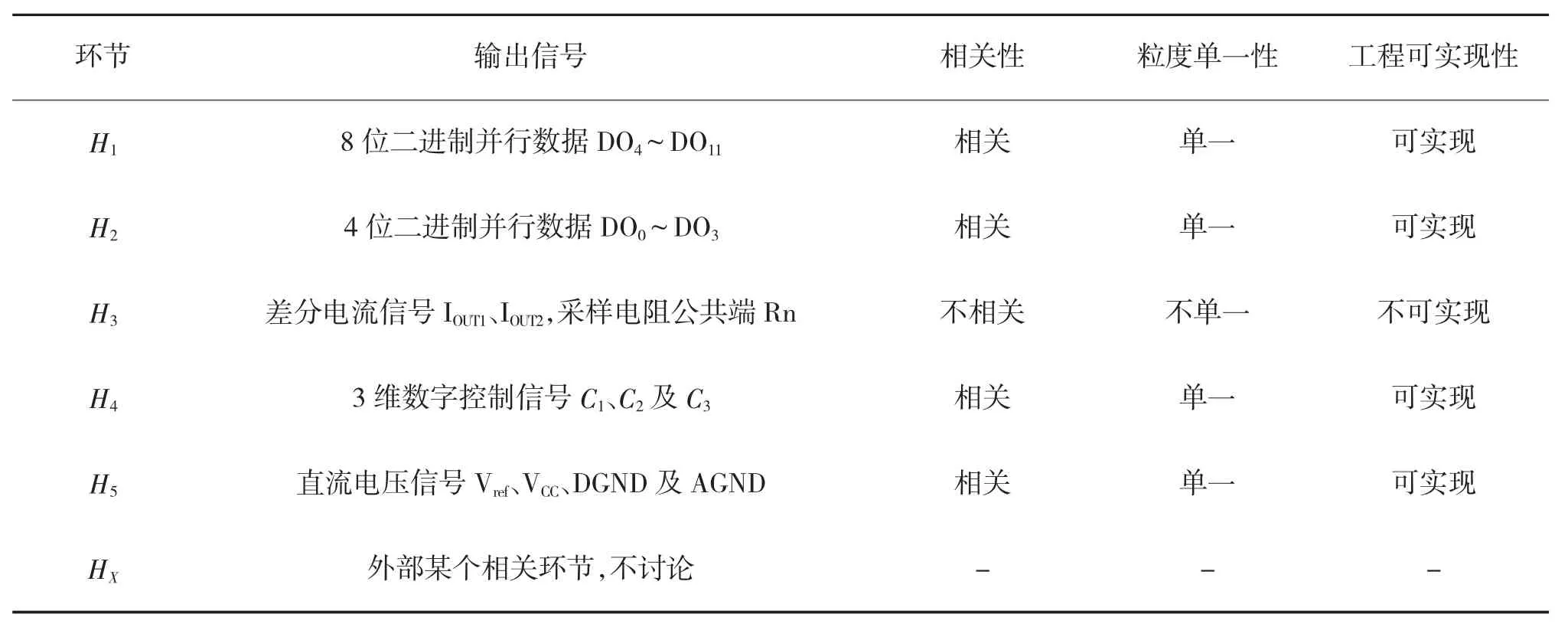
表1 输出信号特性表

3.3 通过粒度的透明性，修正DAC1230芯片环节及传递关系模型，优化模型用于工程检测的适应性

如图4所示模型中，与图3电路原理图对应，其环节输入信号A如下页表2所示。

由表2可知，由于环节H3粒度不透明，该环节不易进行工程测试，因此，将环节H3解聚为环节H31和环节H32，其中环节H3输入信号为12维，等效于信号DO0～DO11，环节H32输入信号为1维，等效于信号Vref，则环节H31及环节H32具有并联相关性，如下页图7所示。解聚后两个子环节的粒度具有透明性，其输入信号为相关信号集，则这两个子环节易于工程检测。

综上所述，通过用粒度作为评价环节及传递关系的指标，确定DAC1230芯片环节及传递关系模型，使DAC1230芯片环节及传递关系模型满足仿真任务的不同层次及分辨率要求，并提高了其工程适应性和可检测性。

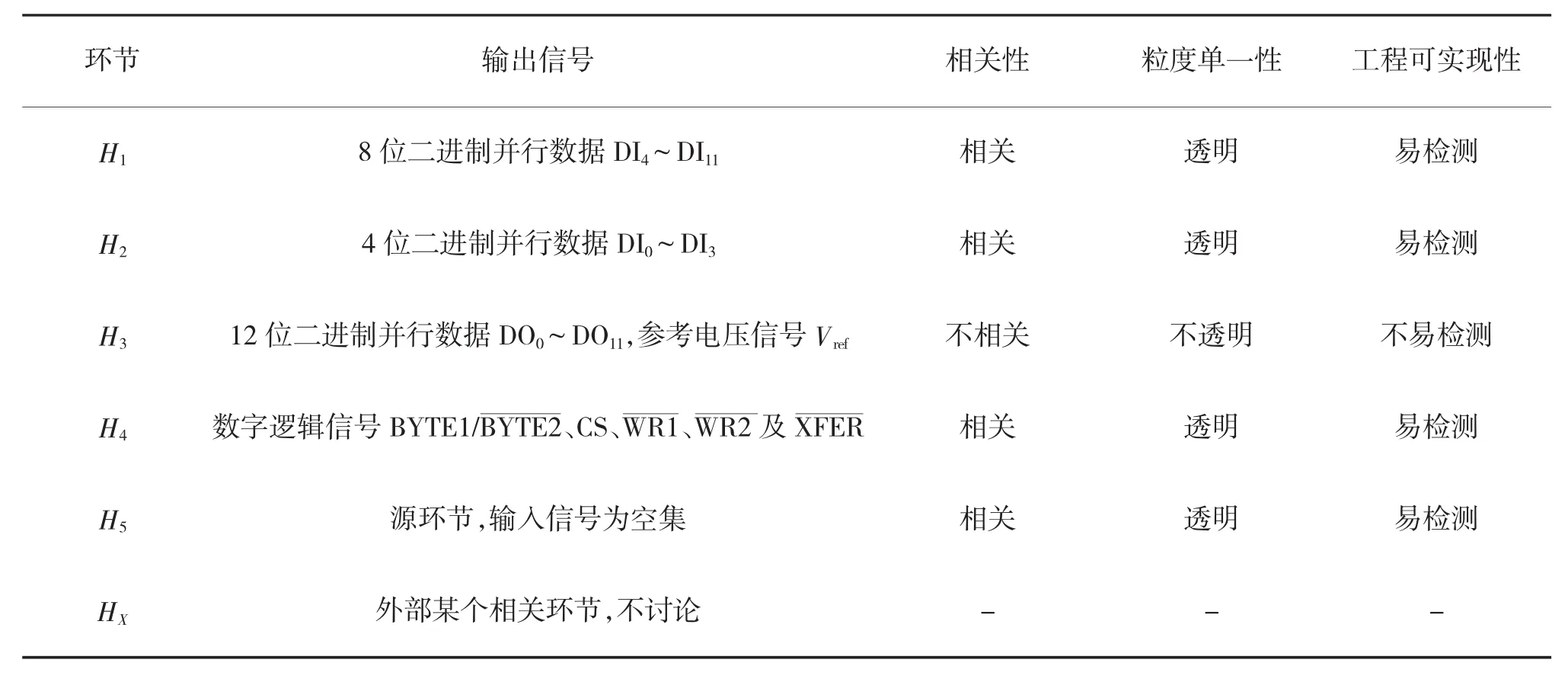
表2 输入信号特性表

图7 修正的环节及传递关系模型

4 结论

本文通过将模型按照功能域划分为若干相关环节及传递关系，采用粒度作为评价环节及传递关系的指标，定义粒度的级别、单一性和透明性3个基本特性来确定该模型结构并进行修正，使环节及传递关系模型满足仿真任务的不同层次及分辨率要求，并提高了其工程适应性和可检测性。

［1］刘延斌，金光.半实物仿真技术的发展现状［J］.光机电信息，2003（1）：27-32.

［2］曹勇，苏欣，邵思杰，等.面向半实物仿真设计的环节及传递关系建模方法研究［J］.军械工程学院学报，2013，25（4）：55-59.

［3］曹勇，苏欣，邵思杰，等.面向故障仿真的环节及传递关系建模方法［J］.装甲兵工程学院学报，2013，27（4）：75-79.

［4］翟俊海，王熙照，张素芳.信息粒度、信息嫡与决策树［J］.计算机工程与应用，2009，45（12）：126-129.