面向不确定文本数据的余弦相似性查询方法*

朱命冬，徐立新，申德荣，寇 月，聂铁铮

1.河南工学院 计算机科学与技术系，河南 新乡 453003

2.东北大学 计算机科学与工程学院，沈阳 110819

1 引言

随着基于位置的服务、传感器网络、人脸识别、人工智能、数据挖掘等技术的流行，不确定数据在现实生活中广泛存在。例如，温度传感器测量出一个地区温度70%的概率为26℃，30%的概率为30℃，即一个事件都以一定的概率发生。而对不确定数据的管理中一个不可或缺操作是查询操作，如查询一个区域范围内平均温度大于30℃的城市。因此不确定性的相似性查询也被广泛关注，如不确定性top-k，不确定性数据连接和不确定性最近邻（nearest neighbor，NN）等[1-6]。随着云计算技术的成熟和处理大数据需求的加剧，分布式计算和云平台下算法的研究成为一种趋势。

随着数据类型多样化和复杂化，互联网中出现了大量的不确定性文本数据。例如对互联网中的图书进行分类时，从不同网站抽取到的同一本书的摘要信息可能是不同的。假设有一本书Book1,从4个网站抽取到的摘要为A11,从6个网站抽取到的摘要为A12,则这本书的摘要以不确定性的形式可以描述为{＜A11,0.4＞,＜A12,0.6＞}, 即Book1={＜A11,0.4＞,＜A12,0.6＞},可设第二本书的摘要信息为Book2={＜A21,0.5＞,＜A22,0.5＞}。那么在计算Book1和Book2这两本书的类别时，不仅仅要计算两本书的摘要内容，还要考虑两本书的摘要权重。再如，对图书网站的评价信息进行抽取时，每一个书评都有其支持度，如图1是《史蒂夫∙乔布斯传》的一条书评，对应每个书评都有“有用”或“喜欢”点击数，代表该书评的支持度。每本书都有许多书评，每个书评都有一个支持度，很明显所有的书及其书评组成一个巨大的不确定性文本数据集。同样的，在微博网站中,每条微博都有点赞数量和转发数量，根据这些数量可以计算出某个微博的支持度。这些文本和对应的支持度组成了不确定性文本数据集。通过这个数据集可以查找潜在的朋友，这会比单纯比较用户属性更全面。类似的应用还有通过影评找相似的电影，通过餐馆的评价找相似的餐馆等。并且面向不确定文本数据基于余弦相似度的相似性查询在组合推荐、实体识别、数据集成等领域都具有广泛应用。例如在读书网站豆瓣网上，人们倾向于阅读书评，从而获得有共同爱好的朋友或者找到和自己读过的书比较类似的书。当数据集比较大时，这些应用都需要一种高效的面向大规模不确定性文本数据集的相似性查询方法。

Fig.1 Areview and support rate of“Steve Jobs”图1《史蒂夫∙乔布斯传》的一条书评及其支持度

从信息检索领域的理论和实践可知，对文本进行分类（例如网页分类，评论的情感分类）常用方法是先将文本转化为TF-IDF向量，然后通过计算对应向量的余弦距离得出文本之间的相似性[7]。余弦相似度考虑了文本本身的词频和全局词频等信息，以及信息论对TF-IDF的理论支持[8]，将文本型的相似匹配转化为数值型的矩阵计算，使其在计算长文本的相关性和相似性时具有更好的严密性和有效性[9-10]。

本文面向不确定文本数据，研究基于余弦相似度的分布式最近邻查询方法，目标是提出一种解决方案。一方面该方法需要提高查询准确度和效率；另一方面该方法需要基于分布式环境处理大规模数据集。基于余弦距离计算不确定性文本的相似性主要优势有：

（1）余弦相似度的计算TF-IDF的理论支持[8]，将文本型的相似匹配转化为数值型的矩阵计算，在整合计算不确定性数据的权重的过程中，纯数据的计算比混合数据和文本的计算效率更高。

（2）目前大数据的应用需求普遍存在，通过对余弦相似距离构建索引，可以支持面向大规模数据的分布式环境下的k近邻(k-nearest neighbor,kNN）、逆向k近邻(reversek-nearest neighbor,RkNN）等复杂查询。

本文提出基于余弦相似度的分布式环境下的不确定相似性查询方法及最近邻查询算法，并给出面向度量空间的逆向最近邻查询算法。本文的主要贡献可概括如下：

（1）通过分析不确定文本数据的余弦相似度计算的特征，提出了高效的相似度计算方法和改进的索引结构sMVP-tree（statistic multiple vantage point tree）。

（2）通过对余弦距离进行转化，提出了一种基于sMVP-tree的相似性查询方法UnCos（uncertain cosine similarity）。

（3）给出了基于sMVP-tree的查询过滤方法，然后在UnCos的基础上提出了分布式kNN查询算法，以及面向度量空间的RkNN查询过滤方法。

（4）通过大量实验验证了本文算法的有效性。

本文组织结构如下：第2章给出了相关工作；第3章介绍了预备知识和本文使用的数据模型；第4章详细描述了本文提出的查询方法UnCos；第5章提出了分布式查询处理算法；第6章给出实验结果与分析；第7章对全文进行总结，并指出进一步的工作方向。

2 相关研究

近年来，面向不确定数据的相似性查询引起了广泛的关注，根据研究对象大致可将现有研究分为两类：针对数值型数据的方法[11-16]和针对文本型数据的方法[17-21]。

在针对数值型数据的方法中，文献[11]针对不确定数值型数据进行研究，分别在欧式距离、欧式平方距离和直角距离的条件下提出了查询期望最近邻（expected nearest neighbor，ENN）的计算方法，这些方法只需要构建线性大小的索引就可以在综合对数或次线性时间代价内计算出ENN。文献[12]提出了查询非零概率最近邻数据对象的高效算法，提出了预估一个数据对象是查询的最近邻的概率的方法，分别给出了返回最大似然估计的最近邻和返回大于一定概率的最近邻的算法。文献[13]提出了在欧式距离条件下面向不确定数据的相似性查询方法，该方法可以返回用户指定概率阈值内的kNN查询。为了处理大规模高维数据，文献[14]通过将空间和时间信息整合构建统一索引的基础上提出了一种快速的kNN查询算法。文献[15]提出了一种概率逆向kNN(probabilistic RkNN,PRkNN)的查询框架，然后基于已有的空间过滤法给出了有效的概率过滤准则，将空间过滤、概率过滤和概率确认方法整合起来提出了新的PRNN算法和PRkNN算法。文献[16]对现有的基于欧式距离计算路网kNN查询方法在内存中计算效果进行了详细比较，提出了改进的增量欧式限制（incremental Euclidean restriction，IER）方法。但现有方法的RkNN查询过滤方法多针对欧式空间，不适用于度量空间，本文提出的RkNN算法可以有效处理度量空间的数据。

在针对文本型数据的方法中，文献[17]提出了面向无结构文本的相似性查询方法，该方法通过有效的词组划分过滤不相关的数据对象。但该方法需要预先查询阈值进行查询过滤。文献[18]提出了在编辑距离条件下面向不确定性字符串的相似连接方法。该方法引入了字符串级不确定性模型和字符级不确定性模型，并基于概率q-gram提出了上界过滤器和下界过滤器，从而提高相似字符串识别效率。文献[19]提出了一种面向近似近邻查询的分布式哈希学习方法 SparkPQ（spark product quantization）。SparkPQ基于一种按行列划分的分布式矩阵，采用分布式K-Means算法实现模型求解和码本训练，利用训练出的码本模型对分布式数据进行编码和索引，最终通过Spark分布式框架实现近似近邻查询系统。Wang等人提出了可以适用于余弦相似度的不确定性文本类型的相似连接方法[20]。该方法通过字符串特征生成策略对候选查询结果进行过滤，但该方法需要预先设置不确定性阈值，阈值大小很难准确地设定使其适合各种场景。现有的针对不确定性文本型数据的相似性查询方法多是集中式方法，文献[3,21]提出了基于MapReduce的不确定性相似性查询方法。文献[3]的方法主要是基于Jaccord距离对两个集合进行相似性连接。与本文最相关的是文献[21]提出的方法，文献[21]利用Voronoi结构将相似的数据对象映射到同一个节点进行相似性查询处理，本文在实验部分和此方法进行了详细的比较。

3 预备知识

本章介绍所使用的基本概念和数据结构。

字符串相似度函数主要用于衡量两个字符串之间的相似度，可大致分为两类：面向词组的相似度方法和面向字符的相似度方法。面向词组的方法有余弦相似度方法、Dice相似度方法和Jaccard相似度方法等；面向字符的方法有编辑距离方法、Q-gram方法和Smith-Waterman算法等。本文主要分析基于余弦相似度的计算方法。余弦相似度是通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。如果两个向量的方向是一样的，则它们之间的余弦相似度是1，如果两个向量的方向是垂直的，则它们之间的余弦相似度是0。

余弦相似度多用在高维正向量空间中。比如在信息检索和数据挖掘领域，一般一个词条被认为是一个维度，一篇文档可以被看作一个多维的向量，向量值代表对应词条在这篇文档中的重要度。已知两个字符串s1和s2的向量s1和s2，则s1和s2的余弦相似度是[22]：

TF-IDF是将字符串转化为向量的常用方法，TF是指一个词条t在一篇文档s中出现的次数，记为tft,s。直观地说，一个词条的频度越大，该词条在文档中的重要性就越高。但是有的词条在别的文档中也普遍存在，不具有区分度。比如一个汽车公司的文档，几乎每篇文档中都有“汽车”这个词。因此一种衡量一个词条是否具有区分度的概率被提出来了。一个词条t的IDF计算方法是：idft=lb(N/dft),其中dft是指包含词条t的文档数，N是总的文档数量。整合两个概念后，词条t在文档s中的TF-IDF为：tfidf(t,s)=tft,s×idft,通过TF-IDF可以计算出词条在文档中的权重。

定义1（度量空间距离函数）设D是一个数据对象域，任意x,y∈D,如果距离函数d(x,y)满足以下条件，则d(x,y)是度量空间距离函数[23]：

面向度量空间的索引方法是通过数据对象之间的距离进行查询过滤，对于索引方法，数据对象的内容及距离计算函数则是黑盒（black-box）。在面向度量空间的索引方法中，MVP-tree（multiple vantage point tree）是较好的常用方法之一[23]。

MVP-tree是一种基于VP-tree的改进索引方法。主要面向如下两方面进行改进：（1）数据空间外部的枢纽点可以对数据空间进行划分，而且在索引中的不同层可以共享枢纽点。这样，一方面可以减少计算代价，另一方面可以对数据空间进行更好的划分。（2）索引的构建过程中，叶子节点中的数据对象保存了从根节点到该叶子节点中枢纽的距离。在查询处理过程中通过这些距离可以减少计算代价，从而提高查询效率。

根据文献[23]，可以得出关于MPV-tree的一个引理。

引理1构建MVP-tree的计算代价是O(nlogmn),其中m是索引节点的出度，n为数据对象的个数。基于MVP-tree进行等值查询的计算复杂度是O(logmn)。

下面给出本文的数据模型。

数据模型：一个不确定数据对象p是由字符串集S={s1,s2,…,sl}和对应的一个集合W={w1,w2,…,wl}组成，其中wi是对应si的支持度，wi∈[0,1]且。用d表示两个字符串的余弦距离函数，即对于任意两个字符串s1和s2,d(s1,s2)=1-CS(s1,s2),其中s1和s2分别是字符串s1、s2的TF-IDF向量，CS是余弦相似度函数。给定余弦距离函数d,两个不确定数据对象p1和p2的期望距离是：

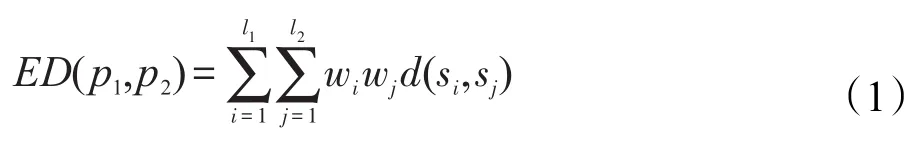
其中，l1和l2分别是数据对象p和q中的字符串个数。

定义2（期望k最近邻）设P={p1,p2,…,pn}是包含n个不确定性数据对象的数据集，对于一个不确定性对象q,q在数据集P中的期望最近邻是ENN(q,P)=argminp∈PED(q,p),q的期望k最近邻(expectedkNN,EkNN)是本文在不产生歧义的情况下EkNN被简写为kNN。

定义3（逆向期望k最近邻）给定一个不确定性对象q,q的逆向期望k最近邻(reverse EkNN,REkNN)是REkNN(q,P)={p∈P|q∈EkNN(p,P)}。本文在上下文清晰的情况下REkNN被简写为RkNN。

4 查询方法UnCos

本章分析基于不确定性文本数据余弦相似度计算的特性，提出面向不确定性文本数据基于余弦相似度的查询方法UnCos。UnCos的构建是基于MVP-tree的改进索引sMVP-tree，在给出UnCos方法之前，首先介绍改进的MVP-tree，称为sMVP-tree。

sMVP-tree的构建过程与MVP-tree的构建过程基本类似，主要区别在于sMVP-tree的构建过程中每个索引节点的分支都保留对应孩子节点所属数据对象的距离统计直方图，直方图表示为histogram(Ni),索引节点Ni是第i个索引节点。如图2所示是索引节点N3中枢纽点p1对孩子节点N4中数据对象的距离直方图histogram(N4)，其中x轴代表距离的划分区间，y轴代表对应区间内数据对象个数。sMVP-tree的构建过程如算法1所示，首先构造一个索引节点（第1行），从数据集中随机选择一个数据对象，计算出该数据对象和其他数据对象距离的中位数，并根据该中位数将数据集分成两部分DS1和DS2（第2～4行），用同样的方法将数据集进一步划分为四部分DS11、DS12、DS21、DS22（第5～9行）。在计算距离中位数的过程中将四部分的距离直方图保存在索引节点中（第10行）。然后对这四部分递归调用构建sMVP-tree算法，直到不可再分，并返回结果（第11～12行）。

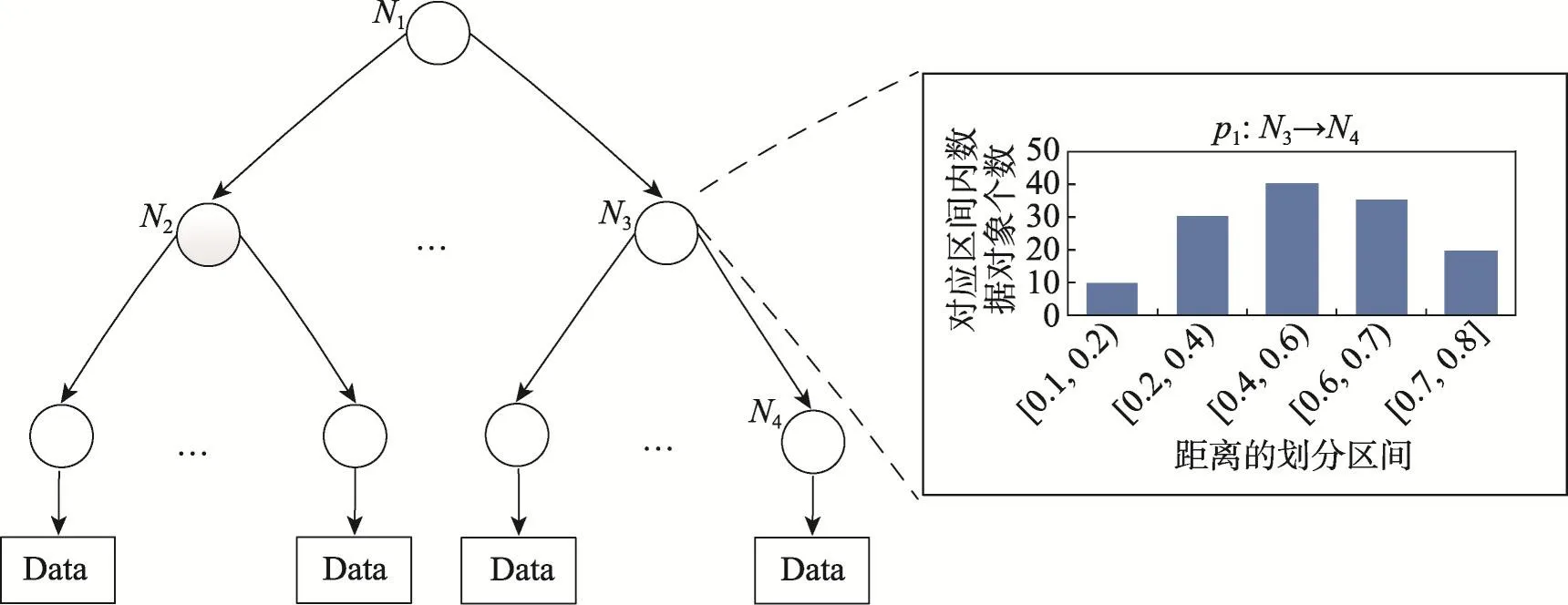
Fig.2 Space partition of sMVP-tree图2 sMVP-tree结构示意图

算法1sMVP-tree构建算法sMVP

输入：数据集DS

输出：sMVP-tree

1.创建根索引节点in

2.P1←从数据集DS中随机选择一个数据对象

3.M1←对于所有ds∈D计算距离d(P1,ds)并得出中位数

4.根据M1将DS划分为两个集合DS1和DS2

5.P2←从数据集DS2随机选择一个数据对象

6.M11←对于所有ds∈DS1计算距离d(P2,ds)并得出中位数

7.M12←对于所有ds∈DS2计算距离d(P2,ds)并得出中位数

8.DS1被M11划分为DS11和DS12

9.DS2被M12划分为DS21和DS22

10.将枢纽数据对象(P1,P2)存入索引节点in中，并且为集合(P1,P2,DS11),(P1,P2,DS12),(P1,P2,DS21),(P1,P2,DS22)构建距离直方图并存入索引节点in中

11.递归调用sMVP(DS11),sMVP(DS12),sMVP(DS21),sMVP(DS22)生成索引节点in的子节点直到叶子节点

12.返回in

根据算法1，sMVP-tree的计算复杂度同MVP-tree一样，多了存储直方图的空间复杂度，因此可以得出引理2。

引理2构建sMVP-tree的计算复杂度为O(nlogmn),m是索引节点的出度，空间复杂度为

根据枢纽点的直方图可以计算出指定距离段的数据对象数量，定义该函数为NumHist(Ni,dist1,dist2),其中dist1和dist2是距离区间，Ni是索引节点i。如果Ni是根节点，则需要对整个索引树的直方图进行计算。

基于sMVP-tree索引结构，提出基于余弦相似度的查询方法UnCos。UnCos主要分为两部分：第一部分是索引构建部分，在不确定数据集上构建sMVP-tree。该部分通过分析不确定性余弦相似度计算的理论特征，给出了高效的相似度计算方法。第二部分是查询处理，基于sMVP-tree进行相似性查询。该部分给出了有查询质量保证的查询方法，并给出了计算复杂度理论分析。下面将对这两部分分别进行详细的介绍。

4.1 索引构建

设P={p1,p2,…,pn},pi={＜si1,wi1＞,＜si2,wi2＞,…,＜sil,wil＞},为了计算不确定字符串间的余弦相似度，将每个字符串视为一个文档，然后计算该文档的TF-IDF向量。令pi={＜si1,wi1＞,＜si2,wi2＞,…,＜sil,wil＞},其中s即对应字符串s的TF-IDF向量。根据式（1）即可计算出不确定字符串间的基于余弦相似度的期望距离。通过分析不确定性余弦相似度的特性，可以给出更快的计算方法，见定理1。

定理 1设，则对于任意pi,pj∈P,

证明根据式（1），又 因 为因此可以得出ED(pi,pj)=定理1得证。 □

通过定理1，不确定性的余弦相似度计算的复杂度可以从O(l2d)减少为O(ld),其中d为TF-IDF向量的维度。

sMVP-tree可以有效地适用于度量空间的最近邻查询，但余弦相似度的计算不属于度量空间。为了有效使用sMVP-tree，首先需要将余弦相似度等价转化为角度相似度。两个字符串s1和s2的角度相似度转化公式如下：

则s1和s2的角度距离可表示为AD(s1,s2)=1-AS(s1,s2)。下面引理3给出了将余弦相似度转化为角度相似度的合理性。

引理3对于任意的不确定对象q∈P,q的角度相似度的最近邻即为q的余弦相似度最近邻。

证明使用反证法，已有一个数据对象q∈P,设p*是q的角度相似度的最近邻，但不是q的余弦相似度最近邻，则根据式（1），存在数据对象p,使得：

又因为对任意p∈P,ED(q,p*)≤ED(q,p),即：

因此至少有一对字符串使得：

令x=CS(q,p),则因为F(x)是单调增函数，所以对∀x1＜x2,F(x1)＜F(x2)。根据式（3），F(CS(q.si,p∗.sj))＜F(CS(q.si,p.sk)),这与式（4）冲突，从而引理3成立。 □

参照引理2，在不确定数据集上的一个sMVP-tree可以以O(ndlogmn+ndl)计算复杂度计算出来，其中d是TF-IDF向量的维度，O(ndl)是计算不确定性数据对象期望的计算复杂度。

4.2 查询处理

构建好sMVP-tree后，当有不确定性最近邻查询q时，首先计算出q的平均点qˉ，然后在构建好的sMVP-tree中查询qˉ的最近邻，最后将qˉ的最近邻返回作为q的查询结果。具体算法见算法2。

算法2UnCos查询算法

输入：查询q和sMVP-tree

输出：q的最近邻查询结果

1.计算出q的平均点qˉ

2.根据索引节点中的枢纽数据对象，从根节点开始计算与qˉ距离最小的孩子索引节点qnode

3.如果qnode不是叶子节点，迭代查找与qˉ距离最小的孩子索引节点

4.如果qnode是叶子节点，则查找叶子节点中与qˉ距离最小的数据对象最近邻

5.返回最近邻

为了保证查询结果的正确性，提出了引理4。

引理4q为一个不确定性查询数据对象，在sMVP-tree中和qˉ的最近邻即是数据对象q的ENN。

证明根据定理1和引理3，此引理易得证。 □

因此，可以通过O(ndlogmn+ndl)的计算复杂度计算出不确定数据对象集的sMVP-tree。当给定 一个不确定查询数据对象q，以O(ld)计算出q的 平均点q，因为最近邻查询是由两次范围查询组成且 以第二次计算复杂度高于第一次，所以可以以在sMVP-tree中找出qˉ的最近邻点并返回结果。其中m为索引树的出度，r为查询的平均选择度，h为sMVP-tree的高度。因此可以得出定理2。

定理2P为一个不确定性数据集，以O(ndlogmn+ndl)的计算复杂度在P上构建sMVP-tree，从而可以以的时间复杂度处理基于余弦相似度的不确定性最近邻查询。

5 分布式查询处理算法

当数据集比较大时，如定理2所示算法的计算复杂度会比较高，因此为了有效处理大规模数据集，本章将算法扩展到分布式环境下，提出分布式kNN算法和分布式RkNN算法。

分布式算法是基于分而治之的思想，如图3所示，P2P分布式系统中各个计算节点是相互独立并自治的。设C是计算节点的数量，PV是数据集的枢纽点集，PV={pvi},其中1≤i≤pn,pn是枢纽点数量。PV作为全局信息存储在各个计算节点上，每个计算节点负责一个或多个枢纽点，数据对象根据数据对象与枢纽点的距离被划分到各个计算节点上，然后各个计算节点在本地构建sMVP-tree。

当有计算节点接收一个不确定性数据对象为q,查询范围为R的查询后，该计算节点会充当协调者，并通过式（5）计算相关的枢纽点：

Fig.3 Data flow of distributed algorithm图3 分布式算法的数据流图

其中maxdi是pvi维护的数据对象中最大的距离。然后协调者会转发查询到相关的枢纽点所在的计算节点上，各个计算节点通过本地sMVP-tree计算出查询结果并返回给协调者。最后协调者收集中间查询结果并返回最终结果给用户。很明显枢纽点的选择和查询算法是系统性能的关键点，接下来具体讨论这两点。

5.1 数据划分枢纽点的选择

（1）枢纽点的选择。枢纽点的主要作用是在查询过程中过滤不相关的数据对象，因此选择枢纽点的指标是尽可能增加查询的过滤能力。在度量空间中一般选择较远的枢纽点[24]，基于这种启发式方法，提出了与文献[23]类似的枢纽点选择方案：

①从样本数据集中随机选择一个数据对象o；

②将样本数据集中距离o最远的数据对象放到枢纽点集PV中；

③将样本数据集中和PV中枢纽点平均距离最大的数据对象加入到PV中；

④重复上一步工作直到|PV|=pn。

（2）查询敏感的负载均衡。在分布式环境中用一致性哈希对枢纽点进行维护和管理，即枢纽点被划分在[0,2max]域上，[0,2max]被划分成多个区间（token），每个计算节点负责一个或多个区间，查询在系统中通过分布式哈希表进行路由。使用较好的哈希方法如SHA1，枢纽点可以均匀地划分在各个计算节点上。但是查询往往不是均匀分布的，而且分布会发生动态变化，因此为了达到系统的负载均衡，需要一种查询敏感的调整方法。首先为负载均衡设置阈值t，如果一个计算节点（NodeA）超过平均负载的t倍，即NodeA成了查询热点，则NodeA与其负责区域相邻的计算节点（NodeB）进行通信，减少NodeA负责的区域并增加NodeB负责的区域，并将相应的枢纽点从NodeA移动到NodeB上。在这个过程中如果别的计算节点产生了负载失衡，则对该计算节点重复这个过程直到实现系统的负载均衡。注意为了避免发生抖动（thrash）现象，负载调整方法要以同一个方向进行。

（3）枢纽点的数量pn的选择。查询处理的计算时间可以分为两部分：一部分是根据枢纽点计算相关计算节点的时间gt；另一部分是各个计算节点进行本地查询的计算时间lt。因此查询处理的计算时间ct=gt+lt。很明显，相关计算节点的计算时间gt和枢纽点数量pn成正比，即gt=α×pn,α是系数比，α的取值和计算节点的处理性能有关；而本地查询的计算时间lt和pn成反比，在平均情况下，其中r是查询对索引树孩子节点的平均选择度，m是索引树的出度，N是数据集的大小，β是系数比，β由计算节点的平均处理性能决定。因此可以得出ct的计算公式：

通过求导并计算极值可以得出，当式（7）满足时：

ct取最小值。通过式（7）可以计算出合适的枢纽点数量。

5.2 分布式查询算法

如本章开篇所述，在该分布式查询模型中利用式（5）易于处理范围查询。下面讨论两种复杂查询处理算法：最近邻查询算法和逆向最近邻查询算法。

5.2.1 kNN查询

先考虑简单情况，k=1时，即为1NN查询，当一个计算节点接收到一个数据对象为q的1NN查询后，该计算节点作为调度者首先以q为查询对象，0为查询半径发起查询，计算相关的枢纽点，即计算出枢纽点集PS={pni|ED(pni,q)≤maxdi},其中maxdi是枢纽节点pni与其维护最远数据对象的距离。然后调度者将查询转发给负责PS集中数据对象的计算节点（表示为CS），各个计算节点计算数据对象q在本地的最近邻并返回给调度者。调度者接收到所有候选最近邻后，计算出与q距离最小的数据对象，设mind是最小距离。之后，调度者以q为查询对象，mind为查询范围计算出相关的枢纽点，向负责这些枢纽点除了CS集的计算节点，转发最近邻查询。最后，调度者收集候选数据对象计算出最近邻，返回给用户。

下面介绍kNN查询算法，具体过程如算法3所示。首先根据统计直方图预估出初始查询距离initR,并计算出相关的计算节点（第1行），对于一个查询对象为q的kNN查询，q与各个枢纽点的距离是qdisti=ED(pni,q),令：

其中，NumHist是第5章定义的直方图中数据对象计算函数。然后将查询转发给相关的计算节点集CS1,各个计算节点计算出本地的kNN数据对象作为候选集返回给调度者，调度者从所有的候选数据对象中计算出最小的kNN候选数据对象的距离mind,并计算出查询范围为mind时相关计算节点CS2（第2～6行），向计算节点集CS1-CS2转发请求，并收集各个计算节点本地的kNN候选数据对象，计算出最终的kNN结果并返回（第7～11行）。

kNN查询算法也是使用两个范围查询实现的，但主要区别是在第一个范围查询时，kNN使用枢纽点中sMVP-tree汇总的直方图信息可以预估出更好的查询范围initR。initR可以对k个最近邻的数据对象有较好的估计，从而有效降低第二次范围查询的代价。

根据算法3的计算过程，kNN查询算法的通信代价由三部分组成：第一部分是收集预估initR的信息，通信代价为O(pn),其中pn为枢纽点数量。第二部分是根据查询半径mind计算出的相关计算节点，通信代价为O(pn)。第三部分是各个计算节点返回的查询结果，通信代价为O(k)。因此可得出kNN查询算法的通信代价为O(2pn+k)。

算法3kNN查询算法

输入：查询q和整数k

输出：q的kNN查询结果

1.根据式（8）计算出initR，进而计算出相关的计算节点CS1

2.将查询q和查询半径initR转发给CS1

3.candity←各个计算节点y∈CS1，计算出本地的k最近邻

4.candit1←汇总所有candity信息，计算出候选的kNN

5.mind←计算出candit1中数据对象与q最远的距离

6.CS2←根据式（5）计算出查询半径为mind时的相关计算节点

7.将查询q转发给计算节点集{CS2-CS1}

8.candity←各个计算节点y∈CS2,计算出本地的kNN

9.candit2←汇总所有candity,计算出候选的kNN

10.finalkNN←汇总candit1和candit2,计算出最终的kNN

11.ReturnfinalkNN

5.2.2 RkNN查询

RkNN也是常用的相似性查询之一，但需要消耗更多的计算代价。在欧式空间中，可以利用空间划分的特性[25]对RkNN构建索引并进行有效的过滤。但在度量空间中，只能使用数据对象之间的距离过滤数据对象，而没有方向性等辅助信息，这使得RkNN查询代价非常高。一个容易想到的简单方法（SimM）是：首先对数据集进行预处理，并计算出各个数据对象的kNN,对应于每个数据对象p存储一个列 表 {＜1,d1＞,＜2,d2＞,…,＜i,di＞,＜2i,d2i＞,…,＜lbn,dlbn＞},其中di是数据对象p和iNN之间的距离，n是数据集的大小。假设有一个RkNN查询q,对于数据对象p,如果满足ED(o,p)≤d2i,其中i=argmini(i＜k≤2i),则p可能是q的查询结果，否则p不是q的查询结果。SimM需要的空间复杂度是O(nlbn),过滤过程的计算复杂度O(n)。很明显这样的计算复杂度过高，下面给出一种基于sMVP-tree直方图的查询过滤方法。设一个RkNN查询对象q,一个枢纽点p及该枢纽点负责的数据对象集O。对于任意数据对象o∈O,如果满足式（9），则o不可能是RkNN查询结果。

NumHist(p,0,|ED(q,p)-ED(o,p)|-ED(o,p))＞k（9）

用式（9）可以从索引节点上过滤到大量不相关的数据对象，从而提高查询效率。如图4，是枢纽点p维护数据对象的直方图，当有一个R3NN查询q时，根据三角不等式，任意数据对象o和q的距离大于o的3NN的最远距离，因此该数据对象集不包含R3NN的查询结果，可以过滤掉。

基于该过滤方法，提出了RkNN算法，见算法4，根据式（9）计算出相关的枢纽点（第1行），将查询转发给相关的计算节点，各个计算节点在本地的sMVP-tree上使用式（9）计算出候选数据对象（第2～3行），利用kNN查询算法过滤出真正的RkNN结果并返回（第4～8行）。

Fig.4 Query filtering ofRkNN图4RkNN查询过滤

算法4RkNN查询算法

输入：查询q和整数k

输出：q的RkNN查询结果

1.根据式（9）计算相关的枢纽点和计算节点集CS

2.将查询q转发给计算节点集CS

3.candity←各个计算节点y∈CS,计算出候选的数据对象

4.For∀oi∈candity

5.canditi←利用算法3计算出oi的kNN

6.Ifq∈canditi

7.将oi放入结果集RS中

8.Endif

9.Endfor

10.ReturnRS

从算法4可以看出，RkNN算法主要由|canditi|次kNN查询算法组成，因此通信代价为O(|canditi|×(2pn+k))。

6 实验测试与分析

6.1 实验设置

实验中使用了两个真实数据集，第一个数据集抽取自著名的读书网站豆瓣读书（http://book.douban.com/），记为Douban，抽取了50万本书籍信息，平均每本书记录了30个评价，根据支持度每个评价被赋予一个概率值。第二个数据集抽取自微博网站（http://weibo.com/），记为Weibo，抽取了10万人的微博信息，平均每个人搜集了45条微博，并且根据喜欢度给定每条微博一个概率值。去除掉TF-IDF值比较低的词组并通过LDA（latent Dirichlet allocation）[26]算法将词组合并，从而使词组数小于500。

实验基于Cassandra实现，分布式集群由20个计算节点组成，计算节点的配置为：Red Hat Linux System 6.1操作系统，IntelCore i3 2100 3.1 GHz CPU和8 GB内存。本文分布式算法的实现主要基于Cassandra系统中P2P的路由协议，并不依赖于其他优化，因此为了客观考察算法的性能，不使用缓存技术和内存数据库系统。

目前没有针对不确定性的基于余弦相似度的相似性查询算法，本文实验主要和两个比较相关的算法进行比较：一个是简单法（SimM），使用MVP-tree而不是sMVP-tree，对于kNN查询使用简单的两次范围查询，对于RkNN查询则使用文中所述的简单策略。另一个较相关方法是DistV（distributed Voronoi）[21]，该方法是一个基于Voronoi图的方法，通过Cassandra系统（http://wi了计算方法的近似度，将计算出的最近邻和ki.apache.org/cassandra/HadoopSupport）的MapReduce扩展实现。本文提出的方法在实验中简称为DistUC（distributed uncertain cosine similarity）。

实验中参数默认值如表1所示。

如第5章所述，构建sMVP-tree的计算复杂度和构建MVP-tree的计算复杂度一样，但空间复杂度要略高于MVP-tree。如表2所示，Weibo中sMVP-tree的空间代价比MVP-tree多28%，Douban数据集中sMVP-tree的空间代价比MVP-tree多30%。因为数据集大小不同，对于Douban数据集的索引空间代价要高于Weibo数据集的索引空间代价。而对于Douban数据集的索引空间代价在分布式环境中是可以接受的，即平均每个计算节点的空间代价约为38.9 MB。

Table 1 Experiment parameters表1 实验参数

为了计算方法的近似度，将计算出的最近邻和人工选出的结果进行比较。具体地说，对于kNN查询，设是真实的结果，o1,o2,…,om是算法查询结果，则近似度为，显而易见近似度越接近1，性能越好。

Table 2 Space cost of sMVP-tree表2 sMVP-tree的空间代价 MB

6.2 定理1的效果

首先通过1NN查询验证定理1对算法性能的影响。在图5和图6中比较了使用定理1和不使用定理1时算法的运行时间和准确度。很明显图5显示了使用定理1时算法的运行时间约是不用时的至图6显示了算法在Douban和Weibo数据集上的近似度，可以看出在Douban上的近似度要好于在Weibo上的近似度。这是因为Douban的评价长度要比Weibo的更长，包含的信息量更大。本文的算法更适合于Douban数据集。

Fig.5 Effect of Theorem 1图5 定理1改进效果

为了验证余弦相似度在处理不确定性文本数据时的优势，图7和图8比较了在Douban和Weibo数据集中分别使用余弦相似度计算和Jaccard相似度计算的运行时间和准确性。从图7中可以看出，在运算时间方面，因为余弦相似度计算方法的计算过程全是数值型运算，效率比混合文本匹配和数值计算的Jaccard相似性计算方法高，进一步通过定理1的优化方法，运行时间约是Jaccard相似性计算方法的至同时，从图8中可以看出，在Douban和Weibo数据集上，余弦相似度计算方法的准确性要优于Jaccard相似性计算方法。

Fig.7 Running time:Cosine similarity vs.Jaccard similarity图7 余弦相似度和Jaccard相似性方法运行时间比较

Fig.8 Accuracy:Cosine similarity vs.Jaccard similarity图8 余弦相似度和Jaccard相似性方法准确性比较

6.3 词组数的影响

图9和图10是在Douban数据集上从100到400变化词组数时进行1NN查询时的实验结果。在度量空间内，查询通过数据对象之间的距离进行过滤，查询效率和数据分布密切关系。因为通过枢纽点的划分使得相近的数据对象在一个计算节点上，词组数的增加没有对性能产生很大的影响，如图所示，查询的计算代价和数据的词组数呈线性关系。图9显示出随着数据集的词组数增加，各个算法的运行时间也在逐渐增加，可以看出在词组数各种取值情况下，DistUC都要比其他两种算法快。图10显示出，随着数据词组数的增加，近似度趋于更好。

Fig.9 Effect of tokens number:running time图9 词组数的影响：运行时间

Fig.10 Effect of tokens number:accuracy图10 词组数的影响：近似度

6.4 kNN查询性能

通过变化参数k来验证kNN查询算法的性能。图11和图12显示了在Douban和Weibo数据集上的kNN算法运行时间。本质上DistUC是由两轮最近邻查询组成，且可以看出DistUC的执行效率要明显好于DistV。图13显示了kNN算法的准确度，在Douban和Weibo数据集上近似值都小于3，说明了算法的有效性。

6.5 RkNN查询性能

最后通过变化参数k来验证RkNN查询算法的性能。图14和图15显示了在Douban和Weibo数据集上的RkNN算法运行时间。从图14和图15中可以看出sMVP-tree的过滤方法明显提高了查询效率，DistUC方法要比SimM方法快一个数量级。图16显示了RkNN算法的准确度，本质上RkNN算法是由多个并行的最近邻算法组成，保持了其较好的近似度。

6.6 负载均衡

Fig.11 Running time ofkNNalgorithm on Douban图11 kNN算法在Douban上运行时间

Fig.12 Running time ofkNNalgorithm on Weibo图12 kNN算法在Weibo上运行时间

Fig.13 Accuracy ofkNNalgorithm图13 kNN算法近似度

Fig.14 Running time ofRkNNalgorithm on Douban图14 RkNN算法在Douban上运行时间

最后通过包含不同比例的kNN查询和RkNN查询的混合查询任务验证系统的负载均衡情况，主要考察3种kNN查询和RkNN查询的比例，分别是（30%，70%）、（50%，50%）、（70%，30%）。实验中通过计算系统中计算节点负载的相对标准差来衡量负载均衡，即，其中xˉ是各个计算节点负载的平均值，δ是各个计算节点负载的标准方差。图17显示了DistUC算法的负载均衡情况，得益于一致性哈希的均衡性和查询敏感的动态平衡性，DistUC算法在不同的查询负载下均表现出良好的负载均衡，相对标准差维持在0.4以下。

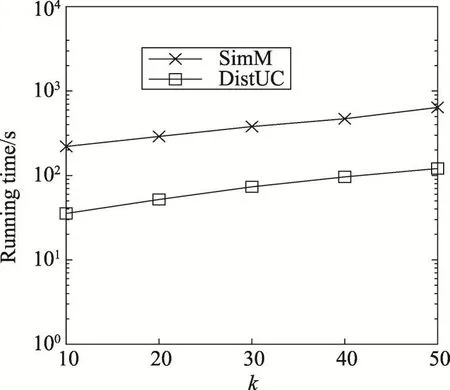
Fig.15 Running time ofRkNNalgorithm on Weibo图15 RkNN算法在Weibo上运行时间

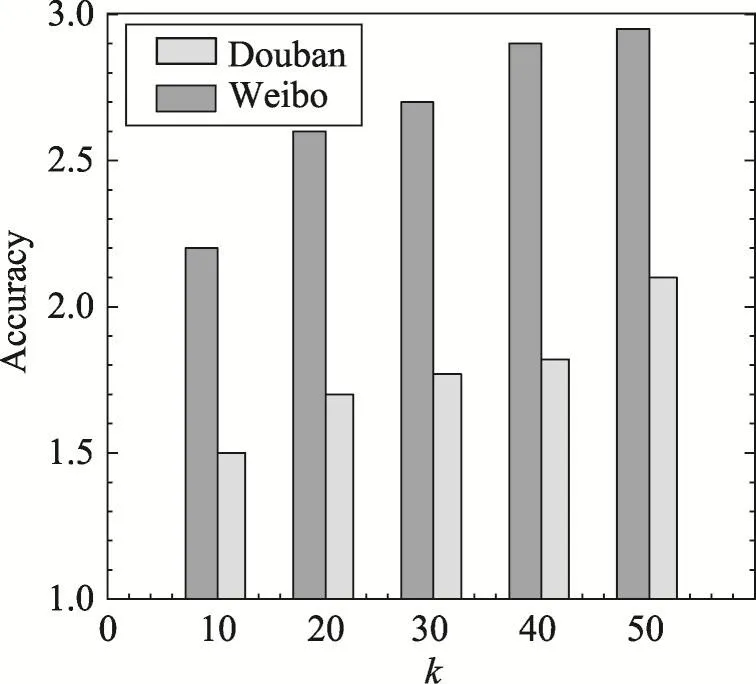
Fig.16 Accuracy ofRkNNalgorithm图16 RkNN算法近似度

Fig.17 Load balance图17 负载均衡

7 结束语

随着大数据的应用急速增长，面向大规模数据的分布式查询处理成为研究热点。本文研究了分布式环境下基于余弦相似度的不确定最近邻查询的问题。首先分析了不确定性余弦相似度计算的特性，并给出了高效的计算方法，提出了基于sMVP-tree的查询方法。然后将算法扩展到分布式环境中，介绍了分布式环境下的kNN查询算法，并首次提出了面向度量空间的RkNN查询和过滤方法。最后通过真实数据上的实验验证了算法的有效性。

[1]Zhang Peiwu,Cheng R,Mamoulis N,et al.Voronoi-based nearest neighbor search for multi-dimensional uncertain databases[C]//Proceedings of the 29th International Conference on Data Engineering,Brisbane,Apr 8-12,2013.Washington:IEEE Computer Society,2013:158-169.

[2]Peng Liping,Diao Yanlei,Liu Anna.Optimizing probabilistic query processing on continuous uncertain data[C]//Proceedings of the 37th International Conference on Very Large Data Bases,Seattle,Aug 29-Sep 3,2011.New York:ACM,2011:1169-1180.

[3]Ma Youzhong,Meng Xiaofeng.Set similarity join on massive probabilistic data using MapReduce[J].Distributed and Parallel Databases,2014,32(3):447-464.

[4]Ye Mao,Lee W C,Lee D L,et al.Distributed processing of probabilistictop-Kqueries in wireless sensor networks[J].IEEE Transactions on Knowledge&Data Engineering,2013,25(1):76-91.

[5]Yi Ke,Li Feifei,Kollios G,et al.Efficient processing oftop-Kqueries in uncertain databases with X-relations[J].IEEE Transactions on Knowledge&Data Engineering,2008,20(12):1669-1682.

[6]Dallachiesa M,Palpanas T,Ilyas I F.Top-knearest neighbor search in uncertain data series[J].Proceedings of the VLDB Endowment,2014,8(1):13-24.

[7]Huang Chenghui,Yin Jian,Hou Fang.A text similarity measurement combining word semantic information with TF-IDF method[J].Chinese Journal of Computers,2011,34(5):856-864.

[8]Robertson S.Understanding inverse document frequency:on theoretical arguments for IDF[J].Journal of Documentation,2004,60(5):503-520.

[9]Han Min,Tang Changjie,Duan Lei,et al.TF-IDF similarity based method for tag clustering[J].Journal of Frontiers of Computer Science and Technology,2010,4(3):240-246.

[10]Wu H C,Luk R W P,Wong K F,et al.Interpreting TF-IDF term weights as making relevance decisions[J].ACM Transactions on Information Systems,2008,26(3):55-59.

[11]Agarwal P K,Efrat A,Sankararaman S,et al.Nearest-neighbor searching under uncertainty[C]//Proceedings of the 31st ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems,Scottsdale,May 20-24,2012.New York:ACM,2012:225-236.

[12]Agarwal P K,Aronov B,Har-Peled S,et al.Nearest neighbor searching under uncertainty II[C]//Proceedings of the 32nd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems,New York,Jun 22-27,2013.New York:ACM,2013:115-126.

[13]Zheng Kai,Fung G P C,Zhou Xiaofang.K-nearestneighbor search for fuzzy objects[C]//Proceedings of the 2010 International Conference on Management of Data,Indianapolis,Jun 6-10,2010.New York:ACM,2010:699-710.

[14]Li Chen,Shen Derong,Zhu Mingdong,et al.kNNquery processing approach for content with location and time tags[J].Journal of Software,2016,27(9):2278-2289.

[15]Bernecker T,Emrich T,Kriegel H P,et al.Efficient probabilistic reverse nearest neighbor query processing on uncertain data[C]//Proceedings of the 37th International Conference on Very Large Data Bases,Seattle,Aug 29-Sep 3,2011.New York:ACM,2011:669-680.

[16]Abeywickrama T,Cheema M A,Taniar D.k-nearestneighbors on road networks:a journey in experimentation and inmemory implementation[J].Proceedings of the VLDB Endowment,2016,9(6):492-503.

[17]Wang Pei,Xiao Chuan,Qin Jianbin,et al.Local similarity search for unstructured text[C]//Proceedings of the 2016 International Conference on Management of Data,San Francisco,Jun 26-Jul1,2016.New York:ACM,2016:1991-2005.

[18]Jestes J,Li Feifei,Yan Zhepeng,et al.Probabilistic string similarity joins[C]//Proceedings of the 2010 International Conference on Management of Data,Indianapolis,Jun 6-10,2010.New York:ACM,2010:327-338.

[19]Wen Qingfu,Wang Jianmin,Zhu Han,et al.Distributed learning to hash for approximate nearest neighbor search[J].Chinese Journal of Computers,2017,40(1):192-206.

[20]Wang Jiannan,Li Guoliang,Feng Jianhua.Extending string similarity join to tolerant fuzzy token matching[J].ACM Transactions on Database Systems,2014,39(1):7.

[21]Akdogan A,Demiryurek U,Kashani F B,et al.Voronoibased geospatial query processing with MapReduce[C]//Proceedings of the 2nd International Conference on Cloud Computing,Indianapolis,Nov 30-Dec 3,2010.Washington:IEEE Computer Society,2010:9-16.

[22]Manning C D,Raghavan P,Schtze H.Introduction to information retrieval[M].New York:Cambridge University Press,2008:113-133.

[23]Bozkaya T,Ozsoyoglu M.Indexing large metric spaces for similarity search queries[J].ACM Transactions on Database Systems,1999,24(3):361-404.

[24]Bustos B,Navarro G,Chávez E.Pivot selection techniques for proximity searching in metric spaces[J].Pattern Recognition Letters,2003,24(14):2357-2366.

[25]Yang Shiyu,Cheema M A,Lin Xuemin,et al.Reverseknearest neighbors query processing:experiments and analysis[J].Proceedings of the VLDB Endowment,2015,8(5):605-616.

[26]Shu Liangcai,Long Bo,Meng Weiyi.A latent topic model for complete entity resolution[C]//Proceedings of the 25th International Conference on Data Engineering,Shanghai,Mar 29-Apr 2,2009.Washington:IEEE Computer Society,2009:880-891.

附中文参考文献：

[7]黄承慧,印鉴,侯昉.一种结合词项语义信息和TF-IDF方法的文本相似度量方法[J].计算机学报,2011,34(5):856-864.

[9]韩敏,唐常杰,段磊,等.基于TF-IDF相似度的标签聚类方法[J].计算机科学与探索,2010,4(3):240-246.

[14]李晨,申德荣,朱命冬,等.一种对时空信息的kNN查询处理方法[J].软件学报,2016,27(9):2278-2289.

[19]文庆福,王建民,朱晗,等.面向近似近邻查询的分布式哈希学习方法[J].计算机学报,2017,40(1):192-206.