集成DEMATEL-ISM的防暴弹药寿命影响因素分析*
张宇飞 ,汪 送 ,段雄义
(1.武警工程大学装备工程学院,西安 710086;2.武警福州指挥学院,福州 350002)
0 引言
防暴弹药作为公安和武警部队执行任务中一种应用广泛的防暴武器,在处置各类群体性突发事件中发挥了极其重要的作用[1]。作为武警部队战备物资中极其重要的一种物资,防暴弹药会受到储存环境应力的作用,性能会随时间的变化而发生改变,其储存寿命及在投入使用过程中的可靠性一直倍受关注。通常专业人员对储存了多年的防暴弹药进行性能检测,结果只能显示所测试弹药是否失效,无法得到防暴弹药发生失效的准确时间[2]。防暴弹药寿命与某些特定因素相关,通过提炼寿命影响因素,分析因素之间的相互影响关系,可以构建因素间的层次结构模型,并可对关键影响因素进行有效辨识。
决策实验室分析法(Decision Making Trial and Evaluation Laboratory,DEMATEL)和解释结构模型法(Interpretive Structural Modeling,ISM)是对复杂系统进行分析和决策的重要方法,两种方法均已得到了广泛应用[3]。周德群等[4]最早提出了集成DEMATEL/ISM构建系统层次结构的方法,并给出了二者集成的理论依据和算法;方爱丽等[5]建立了网络化的DEMATEL方法模型,用于产业经济系统分析;崔和瑞等[6]应用集成DEMATEL-ISM方法对风电项目经济运行影响因素与结构模型进行分析;汪送等[7-8]在提取复杂系统安全事故的致因因素后,给出了集成DEMATEL-ISM方法分析事故致因因素的算法步骤;史丽萍等[9]集成解释结构模型和决策实验室分析法,建立企业应急能力多层递阶解释结构模型;张英芝等[10]结合某汽车缸体加工自动线国产组合机床故障数据,采用基于DEMATEL-ISM对其进行故障相关性分析;吴小东等[11]利用集成DEMATEL/ISM方法得出海洋工程装备产业的发展问题之间的综合影响程度及中心度和原因度,建立反映问题之间相互作用的多层次递阶系统结构模型。鉴于DEMATEL-ISM方法分析因素层次结构的有效性,本文将首先提取防暴弹药寿命影响因素,邀请多位领域专家对因素之间的相互影响关系进行直接评判,并采用熵权方法将多位专家的数据进行集结,以消除个人的主观因素,在此基础上采用DEMATEL-ISM方法划分因素之间的层次结构,给出关键因素,旨在为防暴弹药寿命管理提供决策参考。
1 防暴弹药寿命影响因素分析
不同型号的防暴弹药主要都是由发火机构、保险装置、弹体和主装药4大部分组成[2]。结合专家经验、文献资料提炼出影响防暴弹药储存寿命的主要因素有:发火机构失效、弹体锈蚀及变形、药柱失效等。发火机构、保险装置、弹体这些部件都是机械、电子元件,防暴弹药寿命影响因素如图1所示,领域专家主要根据因素的理化特性来判断因素间的相互影响关系。
防暴弹药中,发火机构主要在击针簧、针刺延期点火管等结构上以及与弹体连接方面存在失效的情况;弹体主要是在高压管、弹筒上存在变形或锈蚀;保险装置主要在保险销、拉环上存在失效的情况;药柱主要是在引爆药剂及主装药剂等在非特定储存环境下存在失效情况;地区气候和储存环境差异主要影响弹体和药剂的性能,运输过程的非人为撞击及在储存过程中的人为失误可能导致弹体及保险装置的失效;指挥员、管理人员在运输、装卸、管理和使用过程中发挥作用不明显也可能导致防暴弹药达不到预计的储存寿命。
图1中虽然提取出了9个影响因素,但是因素重要度及因素间的结构层次并不清晰,因此,下文将基于熵权集结的专家数据,改进集成DEMATEL-ISM方法来解决上述问题。
2 DEMATEL-ISM方法的改进
2.1 DEMATEL-ISM方法集成的理论根据
DEMATEL方法运用图论与矩阵论原理进行系统因素分析,通过系统中各因素之间的逻辑关系构建直接影响矩阵,计算因素的影响程度和被影响度,进而确定因素的中心度和原因度[4]。根据中心度确定因素的重要程度,根据原因度确定因素的属性。ISM方法是一种以定性分析为主的方法,可以分析系统的因素选择是否合理,分析系统因素以及相互关系变化时对系统总体的影响等问题,是定性表示系统构成要素以及它们之间存在着的本质上相互依赖、相互制约的模型。
DEMATEL侧重于分析系统因素相对重要性和划分原因因素与结果因素,ISM侧重于建立系统因素相互影响的系统递阶层次结构模型;基于两者的具有一定的共性,将DEMATEL和ISM进行集成,可达到既简化ISM建模的计算量又同时获得系统因素的相对重要性、性质和相互影响关系链[4]。
2.2 改进DEMATEL-ISM方法步骤
改进DEMATEL-ISM划分系统层次结构的思路如下:通过提取防暴弹药寿命影响因素,熵权集结专家数据,再利用DEMATEL方法推导因素间综合影响矩阵并进行计算;根据整体影响矩阵和可达矩阵的关系,将整体影响矩阵转换为ISM方法中的可达矩阵。根据可达矩阵和ISM方法划分出系统因素的层次结构。
步骤1:确定防暴弹药寿命影响因素a1,a2,…,an,ai∈A(i=1,2,…,n),其中 n 为影响因素的数目,A为影响因素的集合。
步骤2:计算规范化影响矩阵。根据所提取的防暴弹药寿命影响因素,邀请专家 k(k=1,2,…,m)结合自身经验对因素间的直接影响关系进行判定,得到矩阵表示第k位专家给出的寿命影响因素ai对aj的直接影响程度,m为参与评价的专家数量。由于因素间的相互影响关系并非同等,因此,一般情况 aij≠aji,当 i=j时,取 aij=0。为消除专家主观因素的影响,采用熵权对多位专家的数据进行集结。
基于Shannon定义对离散信息源“产生”的信息量进行度量公式[12-13]:
式中,H为第i'(i'=1,2,3,4,5,6)维数据的熵值,K为波尔兹曼常数,K>0,一般取K=1/Inn,i'为转置所得的n×m矩阵中的列,此时j变成行。
第i'维数据的熵权计算式为:
式中,ωi'为第i'维数据的熵权;gi'为差异性系数。
基于矩阵B[βij],所有矩阵元素除以行和的最大值得到规范化直接影响矩阵 C(C=[cij]n×n)
通过规范化处理,使得 0<cij<1,此时规范化直接影响矩阵C对角线上的元素仍为0。
步骤 3:计算综合影响矩阵 T(T=[tij]n×n)。综合影响矩阵表示因素间直接影响和间接影响的综合累加,以确定每一个因素相对于系统中最高水平的因素的最终影响,有
步骤4:计算各影响因素的影响度fi和被影响度ei。基于综合影响矩阵T,将元素按行相加得到因素影响度fi,将元素按列相加得到因素被影响度ei。
步骤5:计算中心度Mi和原因度Ni。影响度fi和被影响度ei相加得到其中心度Mi,影响度fi和被影响度ei相减得到其原因度Ni。
中心度Mi表示该因数i在所有因素中的重要性程度,中心度越大,因素重要度越高。原因度Ni表示该因数i对其他所有因素的因果逻辑关系程度。若为正,表示该因数对其他因素的影响大,称为原因因数;若为负,则表示该因素受到其他因素的影响大,称为结果因素。
步骤6:绘制原因结果图。以中心度为横坐标、原因度为纵坐标绘制笛卡尔坐标系,标出各影响因素在坐标系上的位置,分析各个因素的重要性和属性。
步骤 7:计算整体影响矩阵 H(H=[hij]n×n)
式中,I为单位矩阵。
步骤8:计算标准化可达矩阵。给定阈值λ,得出标准化可达矩阵 K(K=[kij]n×n)
步骤9:确定各影响因素的可达集合以及前因集合。影响因素ai的可达集合和前因集合按下式计算:
式中,Ri表示可达矩阵K第i行中所有元素为1的列对应的要素组成的集合,Si表示可达矩阵K第i列中所有元素为1的行对应的要素组成的集合。
步骤10:验证公式Ri=Ri∩Si(i=1,2,…,n)是否成立。如果成立则说明因素ai为最高层因素,这时在矩阵K中划除第i行和第i列。重复计算直到划除所有因素。
步骤11:根据被划除因素的顺序,绘制因素递阶层次结构图。
3 案例分析
3.1 案例背景
下面举例说明改进的集成DEMATEL-ISM方法划分层次结构的有效性和可行性。.
对某型防暴弹寿命影响因素进行分析,提取了如图 1 所示的 9 个影响因素,分别记为 a1,a2,…,a9。邀请6位领域专家对上述9个因素根据较强、强、一般、弱、无 5 个等级分别赋值 4,3,2,1,0 来确定因素间的直接影响关系,利用熵权法集结数据后,得到直接影响矩阵,见表1。
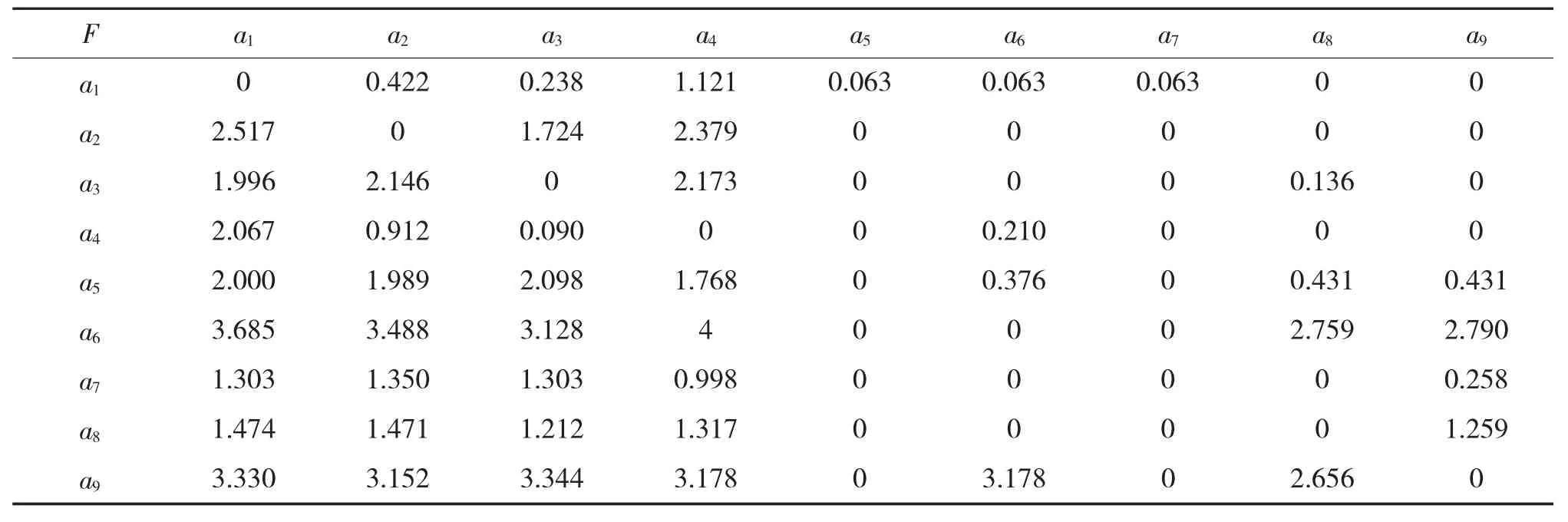
表1 直接影响矩阵
3.2 分析计算
经计算,直接影响矩阵中行和最大值为19.85,根据式(4)可求得规范化矩阵C,进而根据式(5)求得综合影响矩阵T,见表2。
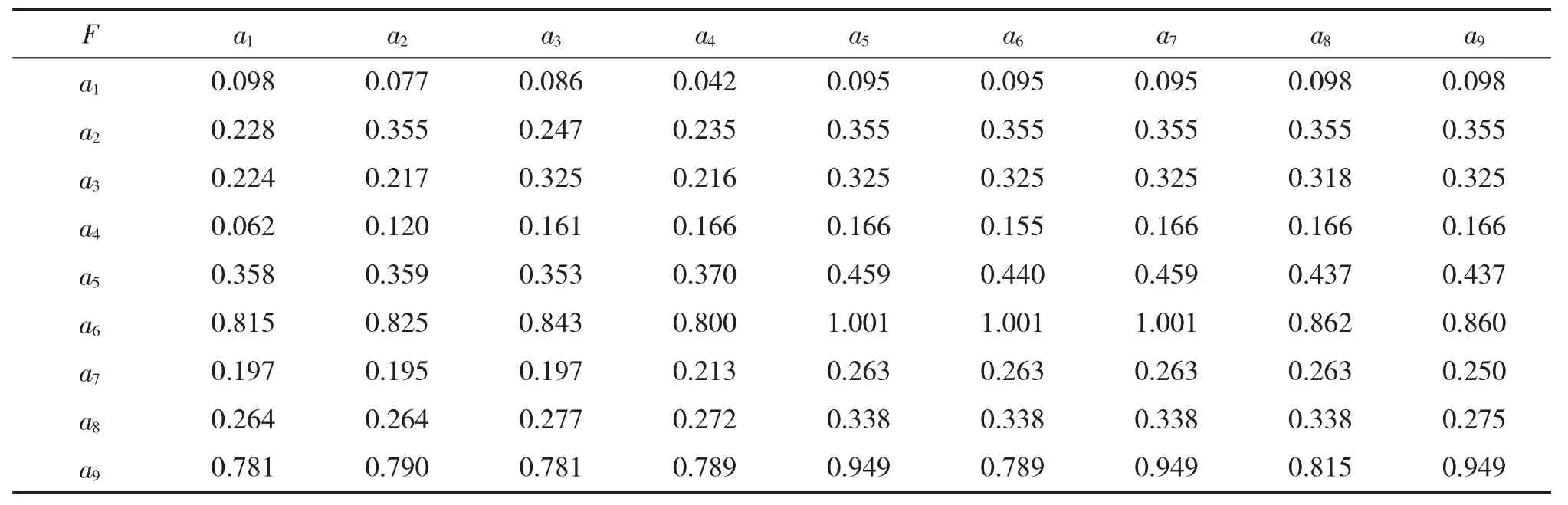
表2 综合影响矩阵
根据步骤4、步骤5的计算公式得到如表3所示的防暴弹药寿命影响因素评估参数和图2所示的因果图。
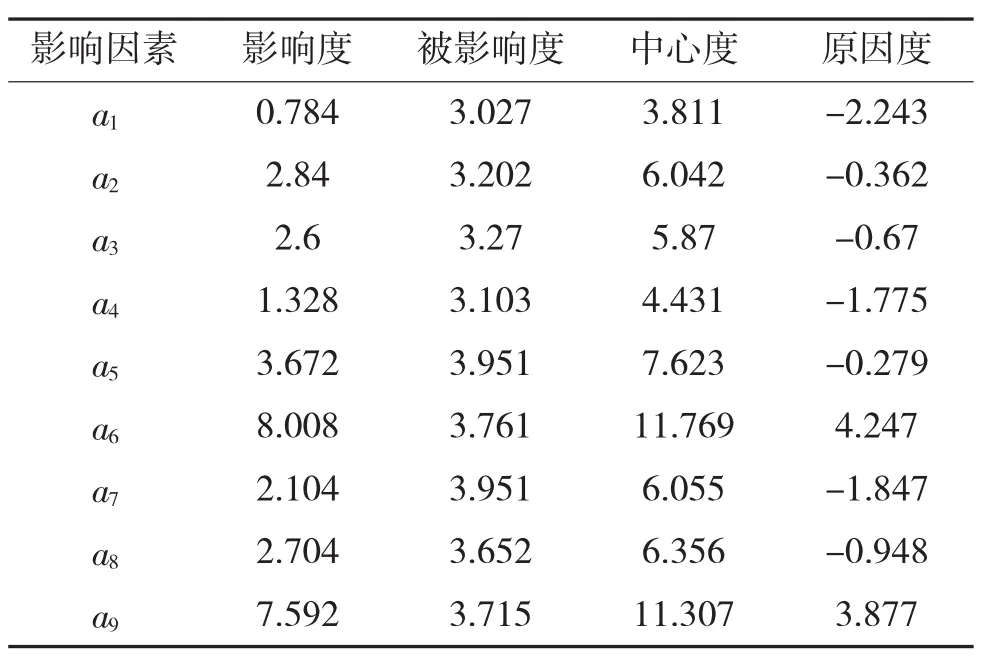
表3 防暴弹药寿命影响因素评估参数
从图 2 可知,储存环境差异(a6)、组织失效(a9)是防暴弹寿命的关键影响因素,也是需要重点预防的潜在因素,取阈值λ=0.3,可得到如表4所示的标准化可达矩阵。
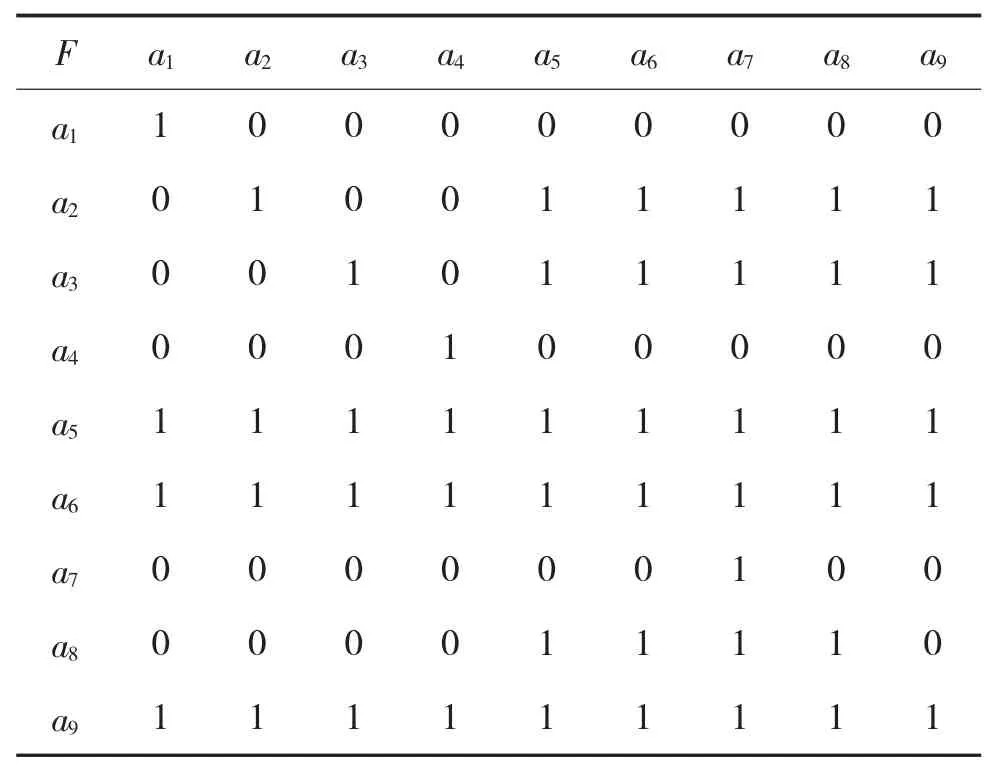
表4 标准化可达矩阵
根据公式Ri=Ri∩Si(i=1,2,…,n),经计算分析得到最高层影响因素集为L1={a1,a4,a7},同理可得L2={a8},L3={a2,a3},L4={a5},最底层影响因素集为 L5={a6,a9}。
根据以上分层结果及标准化可达到矩阵得到如图3所示的防暴弹药寿命影响因素多级递阶层次结构模型。
从图2、图3可知,寿命影响因素6、9是递阶层次结构底层元素,同时中心度又最大,表明这两个因素对其他因素的影响程度和受其他因素的影响程度最大,因此,在防暴弹药寿命管理中,对上述两个因素进行重点管控,可以获得最大的管理效益。
4 结论
在提取防暴弹药寿命影响因素的基础上,邀请多位领域专家对因素之间的相互影响关系进行直接评判,为消除个人的主观因素并保证数据符合客观实际,采用熵权方法对多位专家的数据进行集结,在此基础上分别采用DEMATEL方法获取了关键影响因素,采用ISM方法构建了防暴弹药寿命影响因素多级递阶结构模型。通过实证表明储存环境差异和组织失效是影响防暴弹药储存寿命的关键因素。各部队只要改善库存条件、发挥好组织职能,就可以最大限度保证防暴弹药的寿命尽可能地长,确保防暴弹药的贮存寿命达到出厂时的标准。利用本文所建立的数学模型,对部分催泪弹的贮存寿命进行实际验证,证明了评估结果与实际基本相符。
[1]朱光涛,马永忠,马志伟.防暴弹药储存寿命研究综述[J].化学工程与装备,2016(5):235-236.
[2]郭红霞,庄弘炜.基于成败型试验的催泪弹贮存寿命评估方法[J].火工品,2008(6):45-47.
[3]吴彪,许洪国,戴彤炎.基于DEMATEL-ISM的高速公路作业区交通安全影响因素辨识[J].交通运输系统工程与信息,2010,10(5):130-136.
[4]周德群,章玲.集成DEMATEU/ISM的复杂系统层次划分研究[J].管理科学学报,2008,11(2):20-26.
[5]方爱丽,高齐圣,张嗣流.网络化DEMATEL方法在产业经济系统分析中的应用[J].数学的实践与认识,2009,39(5):78-83.
[6]CUI H R,LI X L,HAO S S.The DEMATEL-ISM analysis on influence factors of economic operation of wind power projects[J].International Journal of u-and e-Service,Science and Technology,2016,9(7):35-42.
[7]WANG S,WANG Y,DU C.Analysis of complex system accident causation network based on DEMATEL-ISM method[J].International Journal of Digital Content Technology and its Applications,2012,6(17):26-35.
[8]杜纯,王瑛,汪送,等.集成DEMATEL/ISM的复杂系统安全事故致因因素分析[J].数学的实践与认识,2012,42(22):143-150.
[9]史丽萍,杜泽文.基于DEMATEL-ISM的企业应急能力结构研究[J].科技管理研究,2013(5):227-230.
[10]张英芝,吴茂坤,申桂香,等.基于DEMATEL/ISM的组合机床故障相关性分析 [J].工业工程,2014,17(3):92-96,127.
[11]吴小东,黄剑锋,赵晶英.基于集成DEMATEL/ISM的海洋工程装备产业发展问题的相互关系分析[J].科技管理研究,2015(4):145-148,161.
[12]汪送.熵权集结多维数据的事故网络节点重要度评估[J].中国安全科学学报,2014,24(5):26-31.
[13]迟宝山,李永泰,李军.基于熵权-双基点研制技术风险评估方法研究[J].科技进步与对策,2006(10):131-133.

