小型冲击式涡轮泵气动效率试验方法研究

王志峰，郝小龙，朱凤琦，张淑敏，郭军刚

(北京精密机电控制设备研究所，北京100076)

1 引言

小型冲击式涡轮泵(以下简称涡轮泵)是航天飞行器伺服系统的核心动力元件。涡轮泵内部的能量转换过程主要有三个：首先是气体内能向气体动能的转换，该转换过程发生于超声速喷嘴内，物理过程近似于绝热等熵过程[1]；其次为气体动能向轴系机械能的转换，转换效率主要为涡轮的气动效率(实际上涡轮内功还需克服轴承和动密封摩擦损耗一部分功[2]，才能输出轴功率驱动泵做功，但这部分损失相对很小)；第三个过程为通过泵组件实现轴系机械能向液压能的转换。因此，表征涡轮泵核心单元涡轮做功能力的气动效率，是设计中的一个重要参数，对其准确测量是研制高性能涡轮泵的基础。

从目前公开的文献看，大部分关于涡轮泵的研究中对于气动效率是先进行CFD仿真，再在试验时测试流场中典型位置点的气动参数，然后与仿真结果进行对比分析确定。其过程实际是对仿真得到的气动流场进行了一次验证，而气动效率仍然是计算值。近年来出现了用电涡流测功机对涡轮轴功率进行测量的方法[3]。该方法通过测量轴的扭矩进而得到轴功率，再与计算的等熵功率相比得到涡轮气动效率，准确度高。但采用该方法时涡轮产生的功率必须由测功机消耗，其耗功形式固定，不适用于涡轮驱动特定负载形式的情况。对于涡轮泵，涡轮与泵叶轮同轴高速运转，后者是前者的特定负载，无法用测功机实现轴功率测量。

在涡轮泵产品研制过程中，由于涡轮与泵结构高度集成，涡轮气动效率的测试问题一直未得到有效解决。传统的研制手段采取理论计算结合经验修正的方式，缺少试验数据支撑。本研究提出一种试验方法，在维持原负载形式的情况下通过测量轴扭矩这一关键数据，得到轴系运转的机械功率，进而得到涡轮气动效率。

2 涡轮泵气动效率理论分析

涡轮泵工作时，工质通过超声速喷嘴膨胀加速，驱动冲击式涡轮，切线泵叶轮与涡轮同轴运转，将高能气体内能转化为液压油压力能，为伺服系统提供动力能源。其结构示意如图1所示。

涡轮气动效率与气动参数和结构有关，在轴系机械损失相对较小的情况下，体现了涡轮输出轴功的能力和水平。一般而言，不同研究者会从不同研究角度出发，使用不同的效率指标[4]对涡轮做功能力进行衡量。本文使用的涡轮气动效率，涵盖了所有与气动过程有关的损失，即考虑了除机械损失(轴承和动密封摩擦损耗)以外的所有损失。在叶轮机械行业，该效率相当于涡轮内效率。

定义涡轮气动效率ηi为涡轮有效比焓降hi与理想比焓降(最大可用焓降)的比值：

式中：∑Δhi为涡轮的主要内部损失，Δhn为喷嘴能量损失，Δhb为动叶能量损失，Δhe为余速损失，Δhδ为二次流损失，Δhf,v为冲击式涡轮局部进气引起的损失。

对于冲击式涡轮，决定气动效率的关键参数是速比u/c1。其中u为涡轮叶片中径处的切向速度，c1为喷嘴出口处的气流速度。气动效率随速比的变化规律如图2所示。由图可知，气动效率对应的最佳速比范围为0.4～0.5[5]。

在涡轮泵研制过程中，涡轮气动效率一般经热力计算求得。

3 试验技术方案

3.1 基本原理

涡轮气动效率可表示为：

式中：P为轴功率，Ni为输入涡轮的总气动功率，ηm为机械效率，T为轴扭矩，n为轴转速，m为涡轮工质质量流量。

式中：R为工质气体常数，k为工质绝热指数，为喷嘴入口总温，为喷嘴入口总压，为喷嘴出口总压。式中各个压力和温度可通过试验实测。

工质质量流量的计算式为：

式中：A为喉部面积。

同样，质量流量也可通过工质压力、温度的实测值和已知的物性参数计算求得。注意，公式中没有考虑流量系数修正，实际流量可能低于计算流量。本研究暂未进行流量标定。

综上，文中气动效率数据是结合轴扭矩测量和等熵焓降计算得到，可称之为准试验数据。要实现对该数据的获取，关键在于轴扭矩的测量。通过搭建涡轮-扭矩仪-泵试验系统，在涡轮泵正常运转状态对轴扭矩进行测量，结合转速数据实测值和气动输入功率计算值，可实现对气动效率的间接测量。

3.2 技术方案及实施

涡轮-扭矩仪-泵试验系统的基本结构如图3所示。试验系统中冲击式涡轮、精密扭矩仪及切线泵共同安装在一个T型槽板平台上，并通过T型槽板上导向凸台进行同轴定位。扭矩仪运转过程中由单独的稀油站为其轴系提供润滑冷却。驱动涡轮与负载泵轴系共用一套润滑油站，分别对轴系统及密封进行冷却润滑。驱动涡轮、扭矩仪及负载泵之间通过高速花键联轴器连接，并分别通过底部垫片进行高度调节。试验过程中，由高压气源驱动涡轮高速旋转输出轴功率，通过高速花键联轴器将轴功率传递至精密扭矩仪的输入端，同时实现转速与扭矩的测量，再通过扭矩仪输出轴及花键联轴器传递给负载泵端做功。冲击式涡轮试验件见图4。

图5、图6分别为一次试验的转速和轴系扭矩数据曲线，可见试验系统在45 000 r/min以上的高转速下可稳定运行。

4 试验结果分析

利用涡轮-扭矩仪-泵组成的气动效率试验系统，开展了不同工质多种工况下的试验测试。提取所需数据信息，并对试验数据进行分析，将涡轮气动效率准试验数据与理论计算值进行比较研究。

4.1 压缩空气工质试验分析

首先利用压缩空气做功能力相对较低的特性，开展了较低转速下涡轮气动效率的测试。对试验工况按热力计算程序进行计算，得到气动效率理论值。表1给出了气动效率试验值与理论值的对比。可见，试验值与理论值吻合度在95%以上，说明在空气介质、低转速下理论计算方法可以得到较为准确的效率预估。

表1 气动效率试验值与理论值的对比(空气)Table 1 Comparison between the test data and calculation results of aerodynamic efficiency(air)

4.2 氦气工质试验分析

以氦气作为驱动涡轮的工质，开展了较高转速下涡轮气动效率的测试。对试验工况按热力计算程序进行计算，得到气动效率理论值。表2示出了气动效率试验值与理论值的对比。从表中可看出，涡轮气动效率理论值比试验值高出20%左右，说明在氦气介质、较高转速下理论计算方法存在一定偏差。

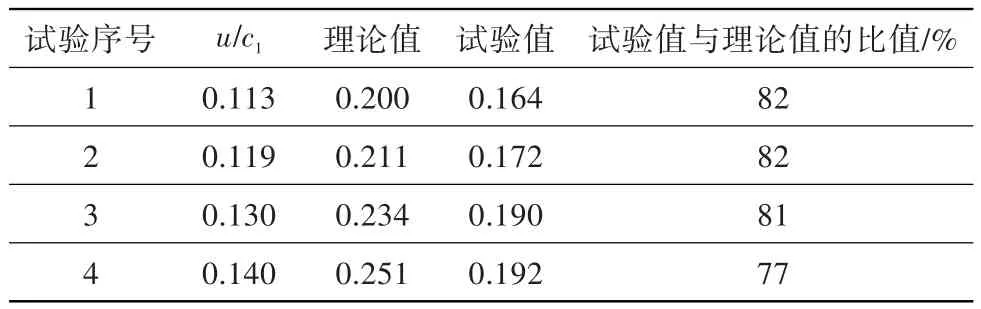
表2 气动效率试验值与理论值的比较(氦气)Table 2 Comparison between the test data and calculation results of aerodynamic efficiency(He)

5 结论

(1)通过将涡轮泵中负载端(泵)与输出功率端(涡轮)进行分体，实现了小型超高速涡轮运转状态下输出扭矩的测量。

(2)通过与试验数据的对比，可以初步确定现有热力计算程序对涡轮气动效率的预估存在一定偏差，目前可测出最大偏差在20%左右。

(3)不同工质下涡轮气动效率理论值与试验值吻合度有差异，说明对于不同工质，理论计算方法应有变化。

[1]王保国，刘淑艳，刘艳明，等.空气动力学基础[M].北京：国防工业出版社，2009.

[2]张远君.液体火箭发动机涡轮泵设计[M].北京：北京航空航天大学出版社，1995.

[3]吴中野，方祥军，刘思永，等.1+3/2级对转涡轮气动性能试验研究[J].北京航空航天大学学报，2016，42(12)：2676—2682.

[4]刘广涛.大膨胀比涡轮机内流场数值计算研究[D].哈尔滨：哈尔滨工业大学，2012.

[5]王仲奇，秦 仁.透平机械原理[M].北京：机械工业出版社，1982.