运用地理加权泊松模型估测天然次生林枯损量分布1)

张凌宇 刘兆刚 董灵波

(东北林业大学，哈尔滨，150040)

天然次生林具有树种繁多、分布范围广等特点，在我国东北、西南和东南地区均有分布，天然次生林不仅作为用材林以及林副产品的重要生产基地，在涵养水源以及维持生态平衡方面等都起到了重要的作用。我国次生林面积约占全国森林面积的46.2%，对天然次生林进行全面规划、改善林分质量，使其尽快成为重要的森林资源。林分枯损影响着森林资源的动态变化，在森林演替过程中也起着至关重要的作用，因此，对天然次生林枯损株数分布的研究具有重要的理论意义。

在20世纪60年代，我国学者就已经开始了对林分枯损的研究，李克志[1]利用带岭地区4种天然林的实测数据，对红松等4种天然林枯损率进行了计算，对各龄组的枯损原因进行了分析；曾伟生[2]利用2006年西藏地区云杉林的实测固定样地数据，在非线性混合估算模型的基础上，构建了云杉林消耗率、枯损率、收获率三者一致兼容的估算模型，这一方法为西藏自治区天然云杉林的枯损量预估提供了参考依据。随着统计模型在林业上的应用，一些学者开始利用全局模型对林分枯损株数进行预测和分析，张雄清等[3]利用落叶松(Larixolgensis)林分连续观测数据，分别利用泊松回归模型、负二项模型、零膨胀模型拟合林分枯损株数。由于在林业调查中所收集的数据往往处于不同的地理位置，无论是研究枯损概率的logistic模型，还是研究枯损株数的泊松模型，实际上都没有考虑到空间异质性，因此，空间异质性在有关林业的各项研究中普遍存在，也往往是研究者最容易忽略的问题。

20世纪90年代，英国学者提出了地理加权回归模型(GWR)，解决空间非平稳性以及空间异质性问题[4-5]。在国内林业领域，有关GWR模型的研究一般集中在森林碳储量以及生物量预估等方面[6-8]，将地理加权回归模型应用到林分枯损株数空间分布中的研究还未见报道。地理加权泊松模型(GWPR)是以地理加权回归模型(GWR)为基础扩展建立的局域泊松模型，可以用来构建以林木枯损株数为因变量的局域模型。本研究采用帽儿山实验林场2期固定样地数据，分别建立了模拟天然次生林枯损株数的全局泊松模型和局域模型，将为大范围内天然次生林枯损株数预测以及解决计数型数据的空间非平稳性问题提供理论基础。

1 研究区概况

帽儿山实验林场位于黑龙江省尚志市西部，地理坐标127°30′～127°34′E、45°20′～45°25′N，总面积26 496 hm2，共划分10个森林经营施业区、151个林班。帽儿山实验林场的植被类型属于长白山植物区系，是地带性顶级植被阔叶红松林被人为干扰破坏后形成的较典型天然次生林。主要林分类型有杨桦林、珍贵硬阔混交林、色木(Acermono)、柞树(Quercusmongolica)为主的硬杂木林,其它主要树种还有水曲柳(Fraxinusmandshurica)、胡桃楸(Junglusmandshurica)、黄菠萝(Phellodendronamurense)、枫桦(Betualcostata)、白桦(Betualplatyphlla)、山杨(Populusdavidiana)等[9]。

2 研究方法

2.1 数据来源

本研究数据来源于帽儿山实验林场森林资源二类调查的2期固定样地数据(2004年和2016年)，在所有的固定样地中剔除宜林沼泽、非林地、农田等样地，同时检查数据中的异常值，对于异常值予以剔除，最终选择101块天然次生林样地作为研究数据，样地面积均为0.06 hm2，数据涵盖研究区内的所有10个施业区。

2.2 模型变量的选择

采用混合逐步选择法对模型变量进行选择，混合逐步选择法是在常规模型的基础上，根据一定的显著性标准，逐步将所选变量剔除或添加进模型的方法[10]，本研究将显著性标准设为α=0.05，最终得到海拔、坡度、林分平均胸径、林分密度和蓄积量共5个影响次生林枯损株数分布的变量。以往国内外研究结果表明，林分枯损株数主要与林分密度、林分平均胸径以及单位面积蓄积量有关[11-12]，同时，林分单位面积枯损株数与土壤因子、立地条件和林分密度有着密切的关系[13]，而坡度以及海拔作为重要的地形因子影响着土壤水分以及养分的含量[14]，间接影响着天然次生林枯损株数分布。在所有的模型中对独立变量均采取了标准化处理，模型各变量的统计量见表1。

表1 模型各变量的基本统计量

2.3 全局泊松模型

全局泊松模型(GP)作为分析计数型数据的一种方法，来模拟天然次生林枯损株数的分布情况，其概率密度函数如下：

(1)

式中：P(Y=y)表示在一段时间内时间Y发生次数的概率；λ为随机变量Y的期望和方差，且期望和方差相等，即E(Y)=λ，Var(Y)=λ；当y=0时，表示天然次生林枯损株数为0的概率；当y=1时，表示天然次生林枯损株数为1的概率；当y=k时，即P(y=k)=e-λλk/k!，表示枯损株数为k的概率。全局泊松回归模型的形式如下：

log(E(Y))=logμ=β0+β1x1+β2x2+β3x3+β4x4+

β5x5。

(2)

式中：log(.)为一个链接函数；μ表示枯损株数；β1～β5为模型的回归系数；x1～x5分别为海拔、坡度、平均胸径、林分密度以及单位面积蓄积量。

2.4 地理加权泊松模型

地理加权泊松模型属于全局泊松回归模型在局域形式上的一种表达，在计算过程中可以将每块样地的地理坐标都纳入到模型中，具体形式如下：

log(e(Y))=logμ=β0(ui,vi)+β1(ui,vi)x1+β2(ui,vi)x2+β3(ui,vi)x3+β4(ui,vi)x4+

β5(ui,vi)x5。

(3)

式中：log(.)为一个链接函数；β1(ui,vi)～β5(ui,vi)为样地点(ui,vi)上的回归系数；x1～x5分别为海拔、坡度、平均胸径、林分密度以及单位面积蓄积量。

2.5 模型残差的空间自相关性分析

真实值与预测值之间的差为模型残差，通过引入莫兰指数(MoranI)这一概念来检验模型残差中的空间相关性，近年来，莫兰指数被普遍运用到在林业研究中[6,15]。全局莫兰指数计算公式如下：

(4)

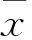
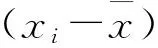
(5)

在研究中，首先设定一个零假设，即当莫兰指数的值为零时，假设模型残差服从随机分布，对于本研究而言，即天然次生林枯损株数的空间随机分布。通过计算莫兰指数，给出一个可以判断出是否拒绝零假设的阈值，称之为Z值，如果Z值在-1.96～1.96的区间内，则P>0.05(α=0.05)，表示不能拒绝模型残差服从随机分布这一零假设，认为模型残差表现出的模式在很大程度上是随机空间过程产生的结果；反之，如果不在这一区间内，则认为模型残差的空间模式不是随机过程产生的，在这种情况下可以拒绝零假设，所表现出来的空间分布模式为具有统计性显著的聚类或分散模式，这种方法可以判断n个样点之间的观测值是否存在空间自相关性[6]。

2.6 模型评价

本研究使用均方误差(MSE)以及赤池信息准则(AIC)值来比较2种模型的拟合效果，当MSE值越小时，说明模型的精度越高，模型的拟合效果越好。具体公式如下：

(6)

赤池信息准则是在熵的概念基础上建立的一种衡量统计模型拟合效果优良的指标[16]，在模型比较时，AIC值越小的模型，说明该模型拟合效果越好。具体公式如下：

AIC=2p-2ln(L)。

(7)

式中：L为最大似然函数值；p为变量个数。

本文采用SAS9.4通过混合逐步选择法对影响天然次生林枯损株数的变量进行筛选，并建立全局泊松模型；采用GWR4.0建立局域GWPR模型，采用ROOKCASE软件来计算全局莫兰指数以及局域莫兰指数，利用反距离权重法(IDW)对局域模型各变量对应参数的空间分布图、局域莫兰指数的空间分布图、局域Z值的空间分布图以及全局和局域模型枯损株数的空间分布图分别进行绘制。

3 结果与分析

3.1 模型拟合

3.1.1 全局泊松模型和局域模型的拟合结果

表2分别给出了全局泊松模型参数估计值、标准误差、显著性检验以及局域模型系数的拟合结果。对于全局泊松模型来说，所有的模型系数均通过了α=0.05水平下的显著性检验，海拔、坡度、林分密度以及单位面积蓄积量的参数估计值均为正值，说明这4个变量与天然次生林枯损株数呈正相关关系，相反地，只有林分平均胸径的参数估计值为负值，说明林分平均胸径与天然次生林枯损株数呈负相关关系。在所有影响天然次生林枯损株数的因子中，林分因子对枯损株数的影响最大，其中林分平均胸径对次生林枯损株数的影响最大，其次是林分密度，最后是单位面积蓄积量，海拔和坡度等地形因子对于次生林枯损株数的影响要小于林分因子。

表2 全局泊松模型和局域模型的参数估计值

全局泊松模型只有一组固定的模型参数，局域模型的参数则是连续变化的，表2给出了5组模型参数统计量，分别为最小值、Q1(四分位数下限值)、中值、Q3(四分位数上限值)以及最大值。

由表2可知，局域模型参数随着地理位置的不同产生了一定的变化范围，在全局泊松模型中β0=1.668 3，β0的参数范围为-0.127 2～3.043 2，同理，在全局泊松模型中β1=0.452 7，β2=0.404 7，β3=-1.427 2，β4=1.128 3，β5=0.966 4，对应局域模型中β1的范围为-1.435 9～1.013 4，β2的范围为-0.238 9～2.044 1，β3的范围为-3.362 9～2.004 8，β4的范围为-1.575 7～5.192 5，β5的范围为-2.967 6～2.829 3。

3.1.2 局域模型各参数的空间分布

从图1A可以看出，在研究区的东南部地区以及东北部小范围内，海拔参数的估计值为负值，说明在这些区域内，随着海拔的逐渐增高，天然次生林枯损株数逐渐减少，而在研究区的中部地区以及西部地区，海拔参数的估计值为正值，说明在这些区域内枯损株数随着海拔高度的增加而增加。

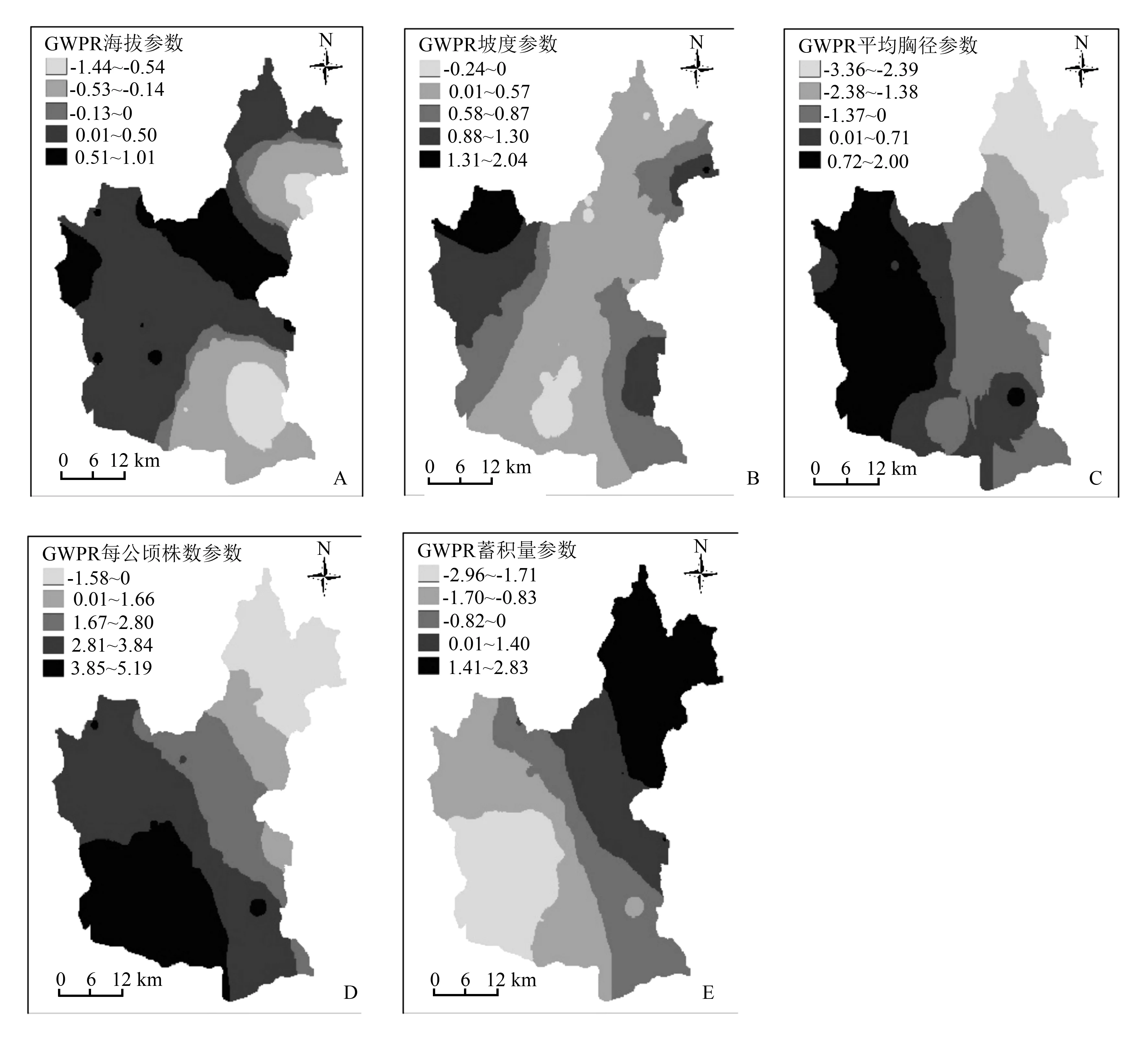
图1 GWPR模型各变量对应参数的空间分布

图1B中，在研究区的北部以及南部地区很小范围内的坡度参数值为负值，所占区域的比例很小，在大部分范围内，随着坡度的逐渐增加，林分枯损株数逐渐增加。

图1C中，西部地区及东南部分地区林分平均胸径的参数估计值为正，说明在这两个区域内，林分平均胸径与枯损株数呈正相关关系，在其他区域内林分平均胸径与枯损株数呈负相关关系，从总体上看，在整个研究区范围内，自西南向东北方向林分平均胸径参数估计值的变化范围从正到负。

在图1D中，林分密度的参数估计值除了在东北部地区极小范围内为负值外，在其他大部分地区林分密度的参数估计值均为正值，说明在这些区域内，随着林分密度的增加，天然次生林枯损株数也随之增加。

在图1E中，林分单位面积蓄积量的参数估计值自东南至西北方向均为负值，参数估计值为负值的区域约占整个研究区域面积的50%，说明在此研究区域内，随着蓄积量的增加，林分枯损株数也随之增加，在其他区域内林分单位面积蓄积量与枯损株数呈正相关关系。总的来说，在局域模型下各参数分级的细化程度较为清晰，同时形成了较好范围内的局域化空间分布效果。

3.2 模型拟合优度比较

根据两种模型的均方误差和赤池信息准则值的计算结果可知，全局泊松模型赤池信息准则值为702.14，局域泊松模型的赤池信息准则值为192.28，说明局域模型在拟合数据的优良性上产生了较好的效果；同时局域模型的均方误差为14.64，全局泊松模型的均方误差值为37.28，说明局域模型的拟合效果要好于全局模型。

3.3 空间自相关性分析

3.3.1 模型残差的全局空间自相关性

图2显示了处于不同空间滞后距离(Lag)状态下，全局泊松模型和局域模型残差的莫兰指数(MoranI)相关图。从总体上看，在空间滞后距离大致相同的情况下，全局泊松模型的莫兰指数值要明显大于局域模型，表明在大部分情况下，全局泊松模型的全局空间相关性要明显高于局域模型；随着空间滞后距离的增加，全局泊松模型的莫兰指数值逐渐减小，而局域模型的莫兰指数值基本在0点上下浮动，起伏没有全局泊松模型明显，说明在降低模型残差全局空间自相关性的效果上，局域模型要明显好于全局泊松模型。此外，全局泊松模型(GP)在空间滞后距离为14 km时，产生最小的莫兰指数值，局域模型(GWPR)在空间滞后距离为5 km时产生最小的莫兰指数值。

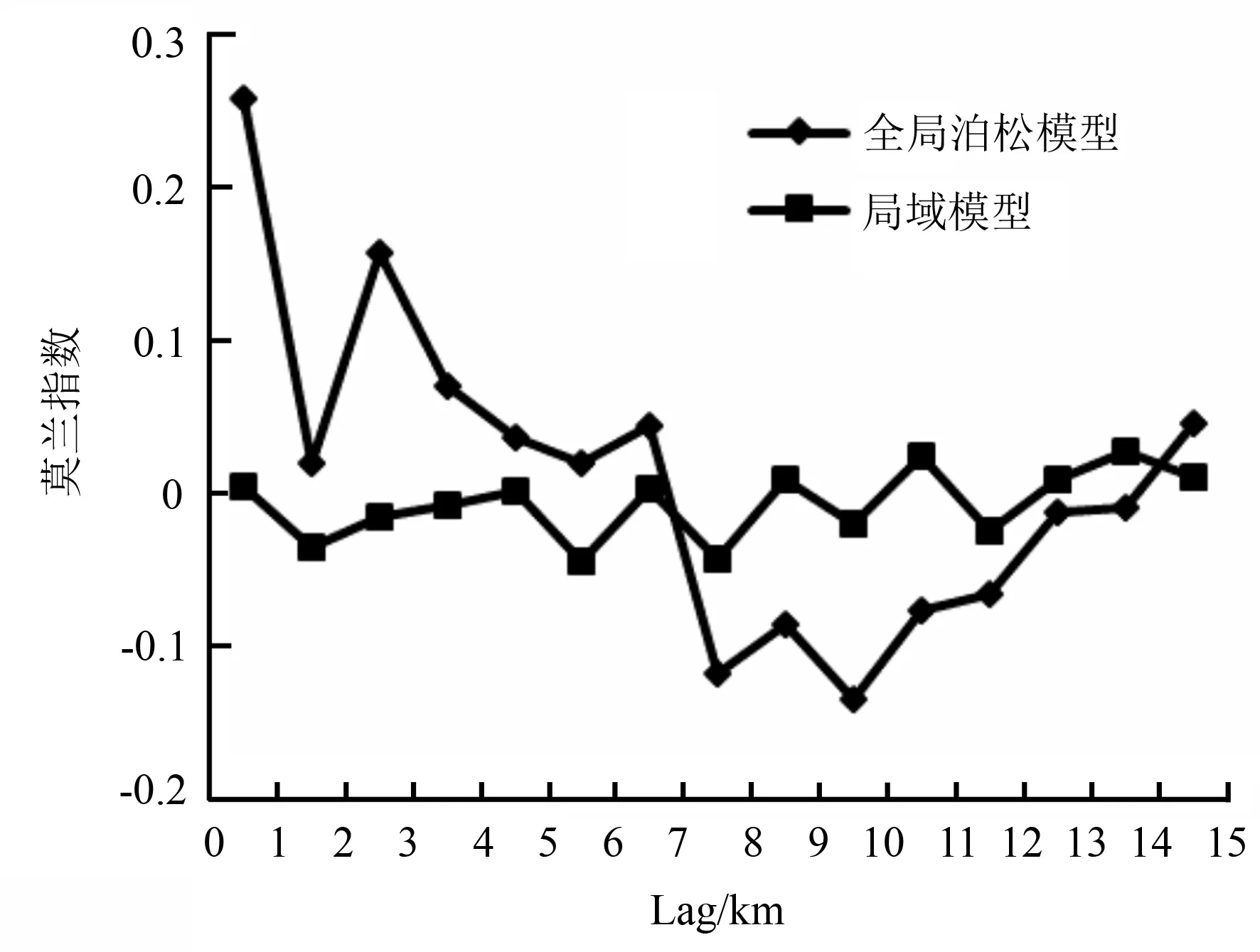
图2 全局泊松模型和局域模型残差的莫兰指数相关图

3.3.2 模型残差的局域空间自相关性

图3给出了全局泊松模型和局域模型残差的莫兰指数值的空间分布图。

由图3A可知，在本研究区域的中部地区，全局泊松模型产生了较大范围且取值为正值的局域莫兰指数值，说明模型残差在该区域内倾向于出现相同观测值的聚类模式；在图3B中，局域模型则在相同区域内产生了取值为负且范围较小的局域莫兰指数值，说明在局域模型下模型残差出现了不同观测值的聚类模式，不同观测值的聚类模式可以很好的揭示空间异质性，产生了较为理想的效果。

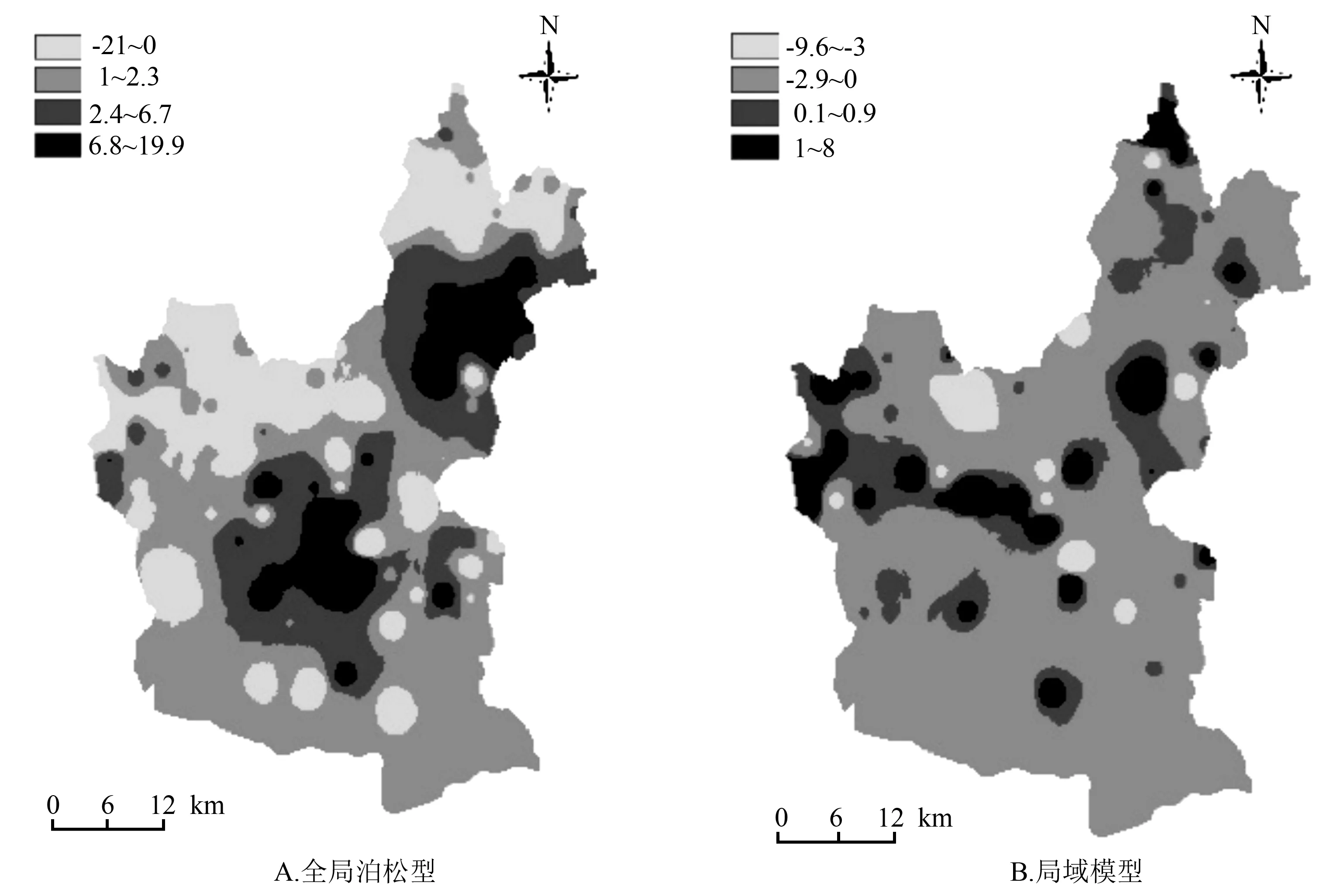
图3 不同模型残差的局域莫兰指数的空间分布

图4给出了在α=0.05显著性水平下，全局泊松模型和局域模型残差局域莫兰指数的Z值空间分布。GWPR模型(图4B)的局域Z值在大部分情况下均在-1.96～1.96，在P>0.05的情况下，各样地点间无显著性差异；全局泊松模型(图4A)的Z值呈现显著性的区域，说明局域模型在降低局域空间自相关性的效果上要明显好于全局泊松模型。

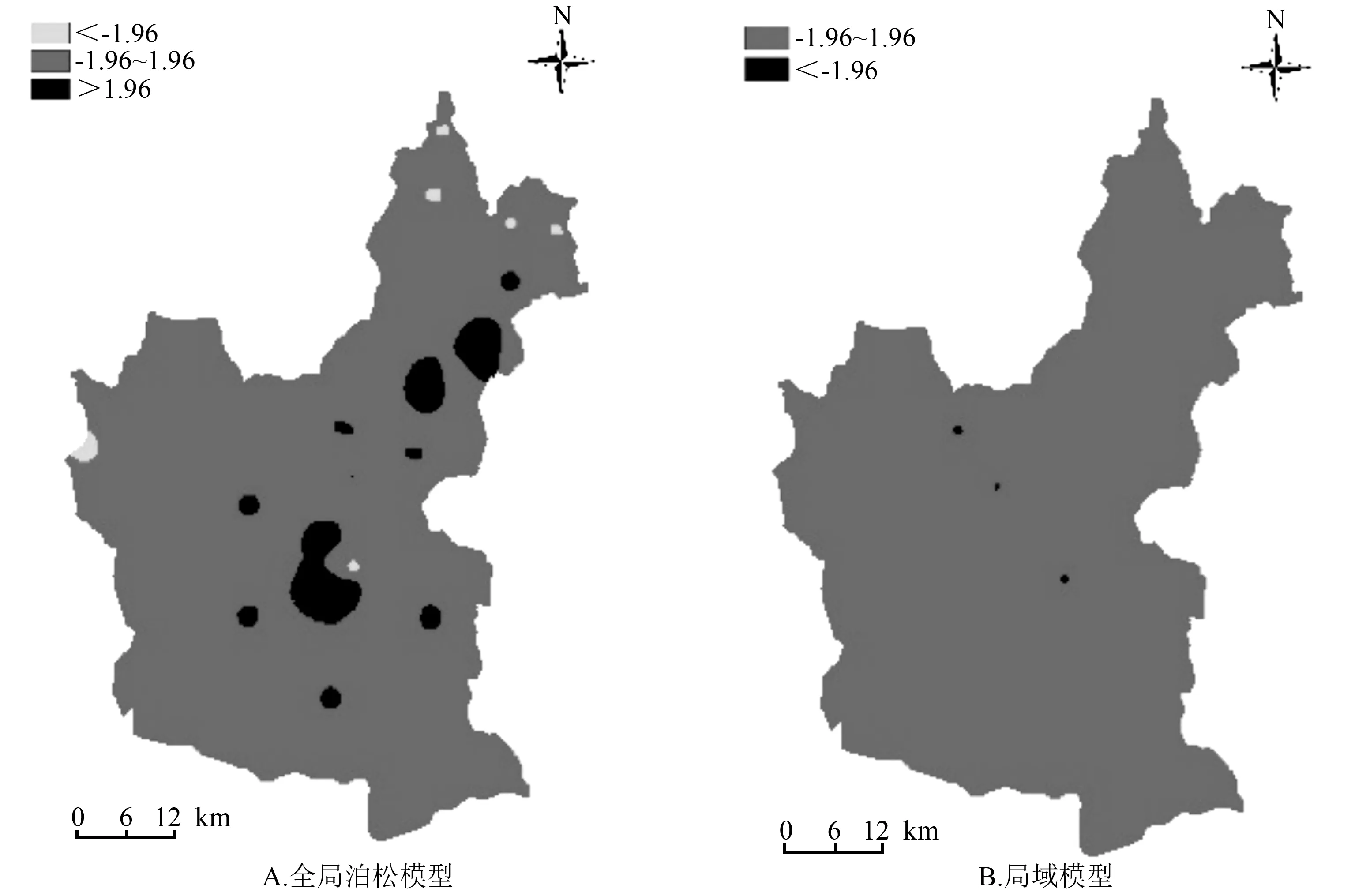
图4 不同模型残差的局域莫兰指数的Z值空间分布

3.4 枯损株数的空间分布

由图5可知，从总体上看，两种模型在对天然次生林枯损株数空间分布的模拟上与样地内实际枯损株数的空间分布大致相同，即研究区的东北部地区林木枯损株数较多，在该地区内两种模型的林木枯损株数均在15株以上；在研究区的东南部地区，全局泊松模型的林木枯损株数在10～15株，而对应局域模型的枯损株数为8～10株；此外，两种模型的拟合偏差存在差异，全局泊松模型对样地内枯损株数模拟的拟合偏差在6株左右，局域模型的拟合偏差在3～4株，要明显低于全局泊松模型，同时在分级的细化程度上，局域模型也要好于全局泊松模型。

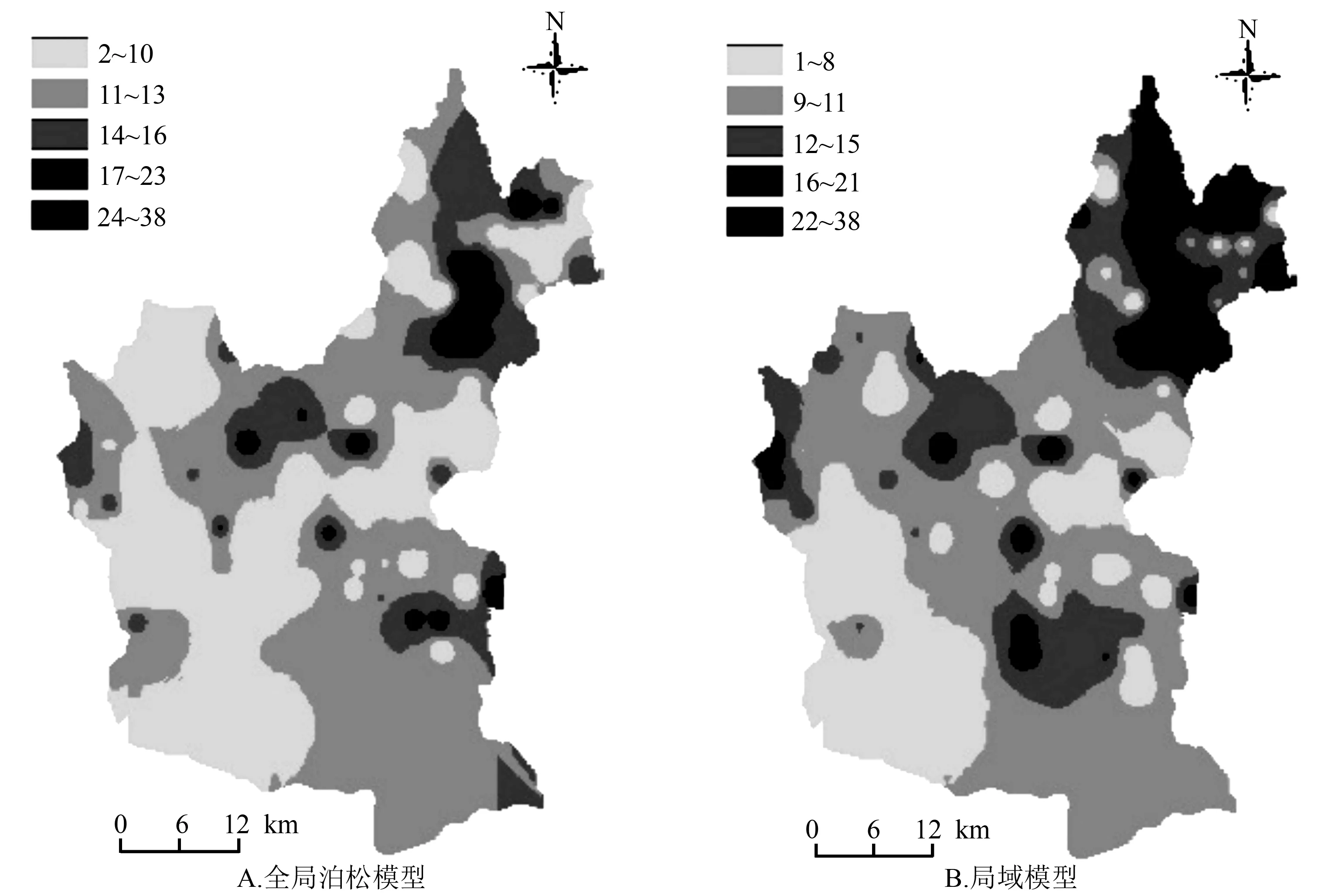
图5 不同模型林木枯损量的空间分布

4 结论与讨论

采用全局泊松模型和局域模型(GWPR)对帽儿山实验林场101块天然次生林样地内的林木枯损株数进行了模拟，并对2种模型的拟合效果以及空间自相关性进行了分析。对于全局泊松模型，林分平均胸径与次生林枯损株数呈负相关关系，且影响最大，对于局域模型来说，随着地理位置的不同，模型参数产生一定的变化范围，各个参数对于枯损株数的影响大小也随之变化；在模型拟合方面，GWPR模型拥有很高的拟合精度，AIC值明显减小，得到了较好的模型参数的局域化空间分布效果；在解决空间自相关性上，GWPR模型残差无论是在全局空间自相关性还是局域空间自相关性上都要小于全局模型，同时产生了不同观测值少量聚类这一理想的空间分布模式；在对枯损株数空间分布的模拟上，局域模型的拟合偏差也要小于全局模型。

在林业数据研究中，一般地势地形不同都会导致研究的数据之间存在空间差异，因此空间自相关性在有关林业的各项研究中普遍存在，同时，泊松模型属于计数模型的范畴，在以往的研究中将GWR模型应用到林分枯损株数空间分布中的研究还未见报道。通过2个模型的空间自相关性分析发现，全局泊松模型的空间自相关性随着空间滞后距离的增加逐渐下降，局域模型的莫兰指数值在0点上下浮动，这是由于局域模型在每块样地内都可以得到一组模型参数，每组模型参数都会形成一个GWPR模型，最后综合成一个模型，局域模型在运行过程中充分考虑了地形因子变化对林木枯损株数的影响，从根本上解决了空间异质性的问题，而全局泊松模型的所有样地只有一组模型参数，在可视化分布图的平滑性以及精度上要小于局域模型(GWPR)。

有关研究结果表明，选取不同的空间尺度可能对空间自相关性的大小产生一定的影响[17-18]，因此，在以后的研究中，应适当结合研究区的面积，选取不同空间尺度下的局域模型，对天然次生林的枯损株数进行探索。此外，本文是以天然次生林为一个整体进行研究的，所选取的天然次生林样地大多为软阔林、硬阔混交林以及软阔混交林。由于天然次生林树种繁多，因此，不同的森林类型可能会导致林分枯损株数的不同，在今后的研究中，可以按照不同林型对天然次生林枯损株数的空间分布进行探讨。

[1] 李克志.小兴安岭带岭林区天然林材积枯损率的初步研究[J].林业科学,1958(1):97-111.

[2] 曾伟生.西藏天然云杉林枯损率与采伐率模型系统研究[J].林业科学研究,2008,21(3):353-356.

[3] 张雄清,雷渊才,雷相东,等.基于计数模型方法的林分枯损研究[J].林业科学,2012，48(8):54-61.

[4] FOTHERINGHAM A S, CHARLTON M, BRUNSDON C. The geography of parameter space: an investigation of spatial non-stationarity[J]. Geographical Information Systems,1996,10(5):605-627.

[5] BRUNSDON C, FOTHERINGHAM A S, CHARLTON M E. Geographically Weighted Regression: A method for exploring spatial nonstationarity[J]. Geographical Analysis,1996,28(4):281-298.

[6] 刘畅.黑龙江省森林碳储量空间分布研究[D].哈尔滨:东北林业大学,2014.

[7] 刘畅,李凤日,甄贞.空间误差模型在黑龙江省森林碳储量空间分布的应用[J].应用生态学报,2014,25(10):2779-2786.

[8] 戚玉娇.大兴安岭森林地上碳储量遥感估算与分析[D].哈尔滨:东北林业大学,2014.

[9] 卢军.帽儿山天然次生林树冠结构和空间优化经营[D].哈尔滨:东北林业大学,2008.

[10] 王济川.Logistic回归模型：方法与应用[M].北京：高等教育出版社,2001.

[12] STEPHENSON N L, FRANKLIN J F. Causes and implications of the correlation between forest productivity and tree mortality rates[J]. Ecological Monographs,2011,81(4):527-555.

[13] 王岳,王海燕,杨小娟,等.基于土壤因子的近天然落叶松云冷杉林枯损模型研究[J].福建农林大学学报(自然科学版),2015,44(4):379-383.

[14] 刘鑫,毕华兴,李笑吟,等.晋西黄土区基于地形因子的土壤水分分异规律研究[J].土壤学报,2007,44(3):411-417.

[15] 刘畅,李凤日,贾炜玮,等.基于局域统计量的黑龙江省多尺度森林碳储量空间分布变化[J].应用生态学报,2014,25(9):2493-2500.

[16] 宋喜芳,李建平,胡希远.模型选择信息量准则AIC及其在方差分析中的应用[J].西北农林科技大学学报(自然科学版),2009，37(2):88-92.

[17] MA Z H, BENJAMI Z, WILLIAM F, et al. Use of localized descriptive statistics for exploring the spatial pattern changes of bird species richness at multiple scales[J]. Applied Geography,2012,32(2):185-194.

[18] GUO L G, MA Z M, ZHANG L Z. Comparison of bandwidth selection in application of geographically weighted regression: A case study[J]. Canadian Journal of Forest Research,2008,38(9):2526-2534.