多元线性回归与神经网络模型在森林地上生物量遥感估测中的应用1)
徐辉 潘萍 宁金魁 臧颢 欧阳勋志 向云西 吴自荣 国瑞 桂亚可 杨武
(江西农业大学,南昌,330045) (江西省林业厅利用外资项目办公室)
森林生态系统是陆地生态系统的主体,在陆地生物圈层和大气圈层之间的碳循环过程中起着至关重要的作用[1]。森林生物量既是森林固碳能力的重要标志,又是评估森林碳收支的重要参数,精确估测森林生物量是量化森林碳汇的关键,因此,森林生物量对森林经营管理和评价具有重要作用[2]。森林生物量的估测方法主要包括样地调查法、通量观测法、模型模拟法、遥感估算法和树木年轮法等[3]。在全球气候变化背景下,如何快速、准确的估测森林生物量及掌握其动态变化规律成为人们关注的热点。遥感估算法以其快速、实时、宏观以及破坏性小等,成为大面积估算森林生物量的主要途径。
利用遥感影像估测森林生物量模型,总体上可分为线性与非线性模型两大类。王雪军等[4]基于MODIS数据及其派生信息、气象信息、地学信息、林分信息等,结合森林资源连续清查的部分样地数据,建立了估测森林植被生物量的多元回归模型,R2为0.44;Eckert[5]利用WorldView-2影像得到了植被指数、主成分以及纹理特征,结合样地实测生物量数据建立了多元线性回归模型,R2达到0.865;汪少华等[6]利用TM影像、森林资源清查数据,构建了临安市森林碳储量人工神经网络模型,R2为0.37,认为人工神经网络模型能够较好的估算大范围的森林碳储量;穆喜云等[7]基于样地和机载LiDAR数据,分别采用了多元线性回归和随机森林回归算法,估算了内蒙古大兴安岭生态站森林地上碳储量,结果表明随机森林回归算法模型的预测精度优于多元线性回归模型,预测精度达到76.38%。综上所述,不同类型的传感器及其在光谱分辨率、辐射分辨率以及空间分辨率上的差异可能会造成估测结果的不同,并且在不同地貌类型、不同的气候带、不同时相所获得的遥感影像反演出的结果也可能会存在显著差异[8-9]。也就是说,对同一类型的模型在不同的区域其估测的精度会有差异,而且不同类型的模型其估测精度的高低也不同。因此,本文以江西省吉水县为研究区域,针对亚热带季风气候和中低山及丘陵为主的地貌,利用遥感影像比较分析多元线性回归模型和BP神经网络模型在估测森林地上生物量的精度,为我国亚热带地区森林生物量的快速估算提供参考依据。
1 研究区概况
研究区位于江西省中部的吉水县,地理坐标为114°38′~115°36′E,26°52′~27°33′N。属于亚热带季风气候区,年平均气温21.5 ℃,年均降水量为1 541.8 mm,年均无霜期290 d。地貌以低山及丘陵为主。全县林地面积168 905.5 hm2,占总面积的65.7%,森林覆盖率达62.6%,境内主要植被类型有针叶林、针阔混交林、常绿阔叶林、落叶阔叶林、竹林等。

图1 研究区地理位置及样地分布
2 研究方法
2.1 材料获取与处理
选取2008年12月1日和12月10日两景Landsat-5卫星接收的TM影像数据,借助ENVI 5.0遥感图像处理软件对其进行辐射定标、大气校正、正射校正及几何校正处理。几何校正控制点误差小于1个像元,采用双线性内插法进行重采样后,设置高斯克吕格投影坐标,然后对影像进行镶嵌并裁剪出研究区。样地数据从2009年吉水县森林资源调查的886个固定样地中筛选出乔木林中有每木检尺(林木调查起测胸径≥5 cm)记录的516个样地(见图1),样地的优势树种主要有马尾松(Pinusmassoniana)、杉木(Cunninghamilanceolata)、湿地松(Pinuselliottii)、木荷(Schimasuperba)、枫香(Liquidambarformosana)、樟树(Cinnamomumbodinieri)、栲树(Castanopsisfargesii)、拟赤杨(Alniphyllumfortunei)、檫木(Sassafrastzumu)等。按照3∶1的比例,随机选取387个样地用于建模,剩余129个作为模型检验样地。乔木层地上生物量采用相关文献对本研究区或与研究区气候、地貌相似地区得出的树种生物量相对生长方程(见表1)计算得到。表1中没有涉及的其他杉类、硬阔、软阔树种分别采用杉木、木荷、拟赤杨的生物量相对生长方程,样地乔木层实测生物量为每株树木的生物量之和;灌木层、草本层地上生物量均采用典型取样方法,从各种林分类型样地中共选取81个,在样地内分别设置3个2 m×2 m的灌木样方、3个1 m×1 m的草本样方,采用收获法测定地上生物量。样地地上总生物量为:
WT=WS+WB+WL+WG+WC。
式中:WT为地上总生物量,WS、WB、WL分别为乔木的干、枝、叶生物量,WG、WC分别为灌木、草本地上生物量。
2.2 模型变量选取
自变量包括遥感变量和地学变量。根据森林生物量与遥感因子、地形因子之间的相关性并参考相关文献[6,16-17],遥感变量选取与地物光谱特征、类型高度相关的原始波段信息(TM1~TM5、TM7)、波段线性组合信息(TM7/TM3、(TM3+TM5)/TM7)、比值植被指数(RVI)、归一化植被指数(NDVI)、差值植被指数(DVI)、主成分变换第一主成分(PC1)、第二主成分(PC2)、第三主成分(PC3)、缨帽变换亮度(TC1)、绿度(TC2)、湿度(TC3)17个变量;地学变量从空间分辨率为30 m的ASTER GDEM数据中提取与样地空间分布相关的坡向(As)、坡度(Sl)、海拔(El)3个变量,DEM影像如图2。

表1 主要树种生物量相对生长方程
注:表中WS、WB、WL分别为乔木的干、枝、叶生物量,D为胸径,H为树高。

图2 研究区DEM影像
2.3 多元线性回归模型
多元线性回归模型在森林生物量的估测中得到了广泛应用[18]。通常以森林地上生物量数据为因变量,以遥感光谱信息、植被指数和纹理特征等为自变量[19],通过多元回归分析构建模型对森林地上生物量进行估算。设固定样地总数为n,地上生物量实测值用向量表示为Yn×1,对应遥感变量和地学变量维数为m,用Xn×m来表示影响生物量的自变量因子,βm×1为未知参数向量,ε为误差项,其均值为零且方差大于零,并假定ε~N(0,σ2)。多元线性回归模型的矩阵表示为:Y=Xβ+ε。
2.4 BP神经网络模型
BP神经网络是指基于误差反向传播算法的多层前向神经网络,通常由输入层、隐含层和输出层组成[20](见图3)。通常把提取的遥感信息、地学信息等作为神经网络的输入信号,神经网络按一定学习规则对输入信号进行正向处理后,在输出端对输出信号进行计算。如果实际输出与期望输出不符,则转向误差的反向传播阶段,并在此过程中修正权值和阈值,如此重复,使网络的实际输出与期望输出不断接近,进而形成估测模型反演森林地上生物量。

图3 BP神经网络结构

2.5 模型精度评价指标
采用决定系数(R2),均方根误差(RMSE)和精度(P)来评价模型的精度,计算公式如下:

3 结果与分析
3.1 多元线性回归估测值
运用SPSS19.0软件,将17个遥感变量、3个地学变量作为自变量,样地实测生物量值作为因变量,采用逐步回归筛选出TM3、TM4、TM5、TC2、TC3、NDVI、El等7个自变量,得到线性回归模型如下:
Y=0.116×TM3-0.069×TM4+0.015×TM5+0.055×TC2+
0.042×TC3+141.584×NDVI+0.049×El-44.306。
模型决定系数R2为0.49,F统计量值为23.164(P<0.01)。这表明回归分析中的样地生物量与建模因子极显著相关,模型的拟合效果较好。
由图4可知,样地生物量预测均值为40.3 t·hm-2,低于样地实测均值(经计算样地生物量实测均值为50.29 t·hm-2)20%。
由图5可知,预测生物量高于实测生物量的样地个数为56个,低于实测生物量的样地个数为73个,偏差幅度为-110.24~38.09 t·hm-2。
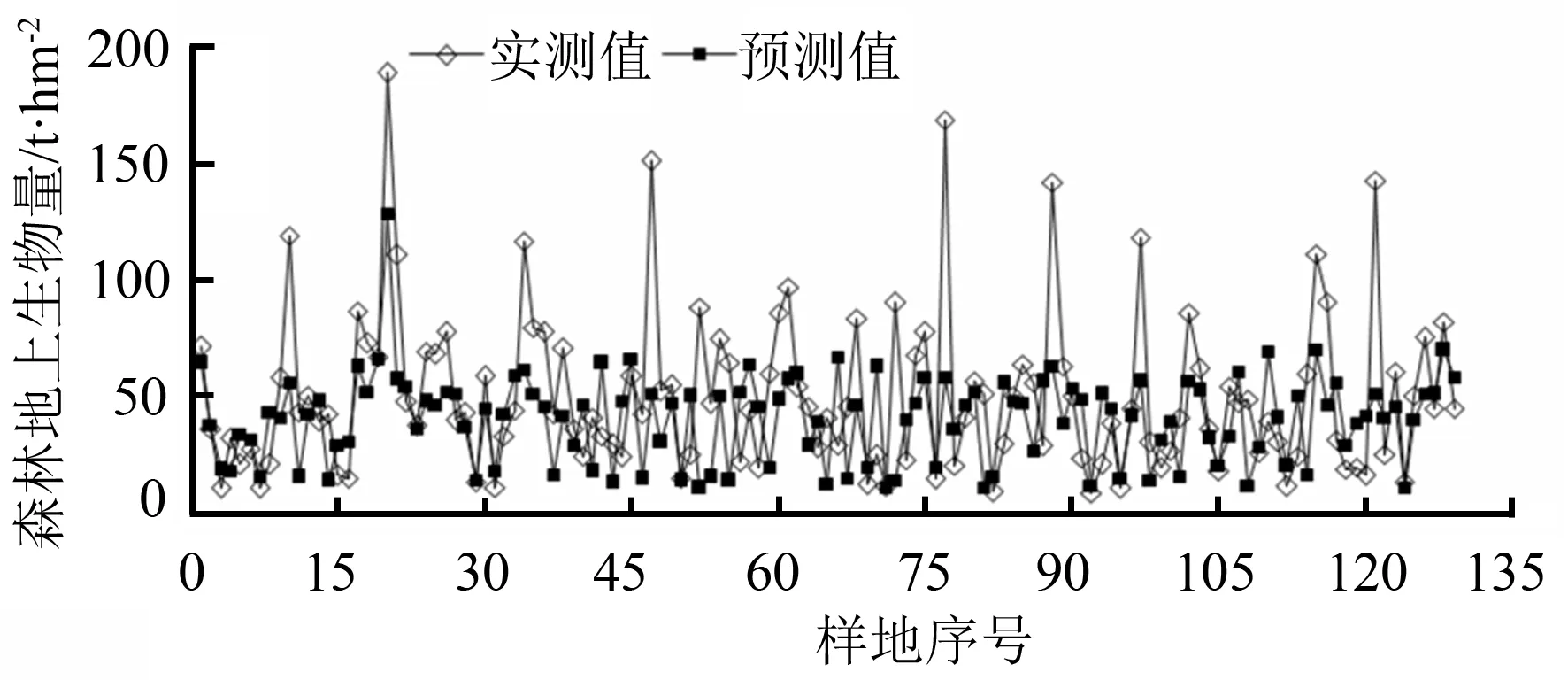
图4 多元线性回归模型预测值与实测值对比

图5 多元线性回归模型生物量预测偏差
3.2 BP神经网络模型估测值
由图6可知,通过对隐含层神经元个数及目标误差的每个不同组合进行10次训练,然后取平均值,最后得到66个组合的预测值与实测值的均方根误差(RMSE),选取RMSE最小时所对应的组合,即隐含层神经元个数与目标误差组合为(7,0.000 1)时,预测值与实测值均方根误差(RMSE)最小,网络训练最优。

图6 组合训练预测值与实测值均方根误差
由图7可知,将检验样地数据代入建立的BP神经网络模型中,得到相应的生物量预测值,并与实测值对比。样地预测生物量均值为47.04 t·hm-2,低于样地实测值6.5%。
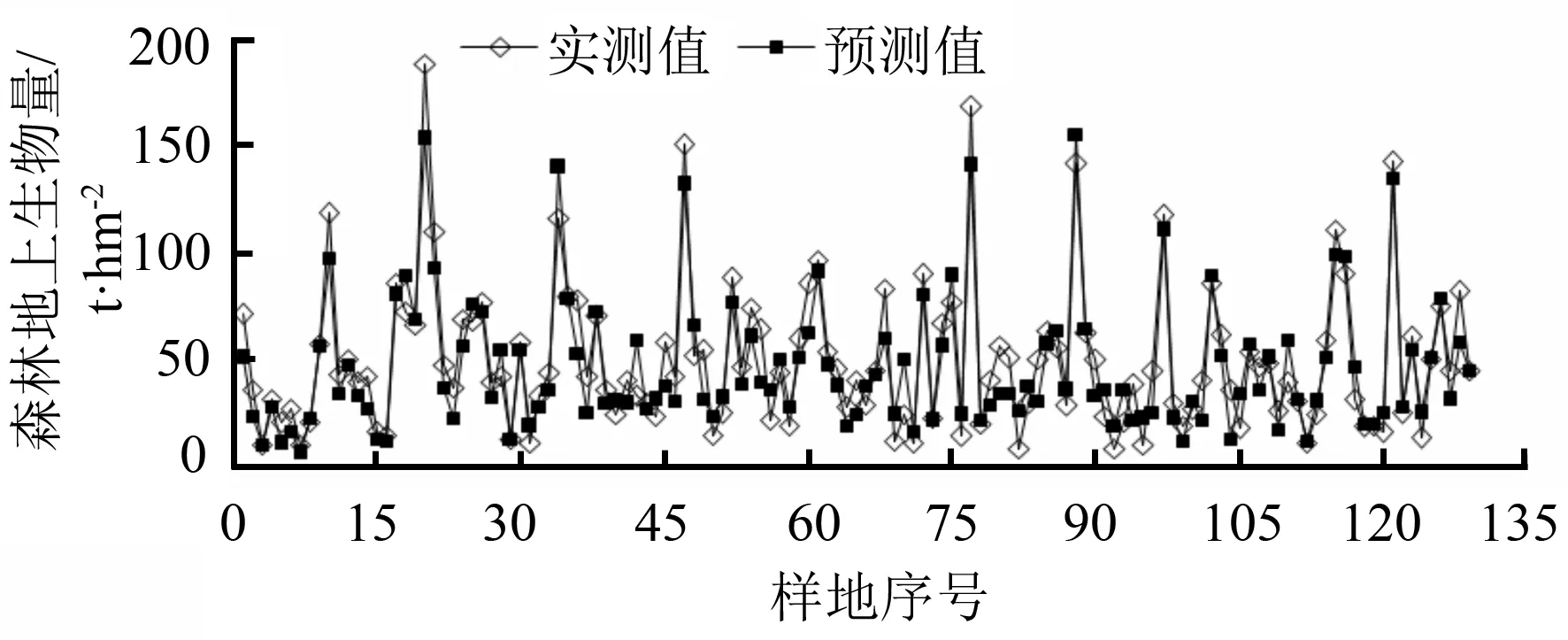
图7 BP神经网络模型预测值与实测值对比
由图8可知,预测生物量高于实测生物量的样地个数为52个,低于实测生物量的样地个数为77个,偏差幅度为-35.12~26.17 t·hm-2。

图8 BP神经网络模型预测偏差
3.3 模型精度
由表3可知,BP神经网络模型在3个精度评价指标上都高于多元线性回归模型,BP神经网络模型的精度比多元线性回归模型高出21.58%,表明运用BP神经网络模型估测森林地上生物量优于多元线性回归模型。

表3 两种模型精度评价
4 结论与讨论
运用TM影像以及森林资源调查固定样地数据,构建的森林地上生物量多元线性回归及BP神经网络估算模型的预测精度分别为50.07%和71.65%,两种模型预测值与实测值的偏差幅度分别为-110.24~38.09、-35.12~26.17 t·hm-2。这表明BP神经网络模型优于多元线性回归模型,与国庆喜等[23]、翟晓江等[24]研究的结论相一致。但模型的预测精度还是有差异,这是因为不同地区地貌、植被类型的差异对精度产生了一定的影响,以及选择不同的自变量因子对模型精度的影响也不相同[25]。
目前利用遥感影像估测森林生物量时多数学者采用多元线性回归模型,其精度也差异较大。蒋云姣等[26]以9个植被指数、3个地形指数为自变量,建立多元线性回归模型估测西峡县森林地上生物量,模型精度仅为21.5%,范文义等[27]将TM影像纹理信息参与森林生物量的估测,得到多元线性回归模型预测精度为75%,造成这种差异的原因与选择的自变量因子有关。蒋云娇等[26]在建模时未选择原始波段信息,因为TM影像的红外、近红外波段与森林生物量具有较强的相关性[8,23,28-29]。此外,纹理信息对森林生物量的估测也具有重要作用[5,30-31],但对于纹理信息的加入将会多大程度提升模型精度还有待进一步研究。
在采用非线性模型估测森林生物量方面,其精度与模型参数的选取关系较大。汪少华等[6]采用人工神经网络模拟临安市森林碳储量及分布时,目标误差选择0.008,并确定了隐含层神经元个数为12,模型估测精度最高,R2为0.37;王轶夫等[32]在选取BP神经网络最优算法确定隐含层神经元个数为8时,模型最优,R2达到0.956。本研究则根据经验公式将隐含层神经元个数与目标误差组合训练,得到组合为(7,0.000 1)时,模型最优,R2为0.869。这表明合理的选取神经网络参数能够进一步提高模型的预测精度。
[1] HOUGHTON R A. Aboveground forest biomass and the global carbon balance[J]. Global Change Biology,2005,11(6):945-958.
[2] 胥喆,舒清态,杨凯博,等.基于非线性混合效应的高山松林生物量模型研究[J].江西农业大学学报,2017,39(1):101-110.
[3] 邵全琴, 杨海军, 刘纪远, 等. 基于树木年轮信息的江西千烟洲人工林碳蓄积分析[J].地理学报,2009,64(1):69-83.
[4] 王雪军, 孙玉军.基于遥感地学模型的辽宁省森林生物量和碳储量估测[J].林业资源管理,2011(1):100-105.
[5] ECKERT S. Improved forest biomass and carbon estimations using texture measures from worldview-2 satellite data[J]. Remote Sens,2012,4(4):810-829.
[6] 汪少华,张茂震,赵平安,等.基于TM影像、森林资源清查数据和人工神经网络的森林碳空间分布模拟[J].生态学报,2011,31(4):998-1008.
[7] 穆喜云,刘清旺,庞勇,等.基于机载激光雷达的森林地上碳储量估测[J].东北林业大学学报,2016,44(11):52-56.
[8] 郭志华,彭少麟,王伯荪.利用TM数据提取粤西地区的森林生物量[J].生态学报,2002,22(11):1832-1839.
[9] 段祝庚,赵旦,曾源,等.基于遥感的区域尺度森林地上生物量估算研究[J].武汉大学学报(信息科学版),2015,40(10):1400-1408.
[10] 杜虎,曾馥平,王克林,等.中国南方3种主要人工林生物量和生产力的动态变化[J].生态学报,2014,34(10):2712-2724.
[11] 杨桦,詹有生,曾志光,等.吉水三种造林模式林分生物量及生长量研究[J].江西农业大学学报,2004,26(2):164-168.
[12] 姚迎九,康文星,田大伦.18年生樟树人工林生物量的结构与分布[J].中南林学院学报,2003,23(1):1-5.
[13] 钱国钦.枫香人工林净生产量动态变化研究[J].江西农业大学学报,2000,22(3):399-404.
[14] 左舒翟,任引,翁闲,等.亚热带常绿阔叶林9个常见树种的生物量相对生长模型[J].应用生态学报,2015,26(2):356-362.
[15] 柳江,洪伟,吴承祯,等.天然更新的檫木林的生物量和生产力[J].热带亚热带植物学报,2002,10(2):105-110.
[16] 毛学刚,王静文,范文义.基于遥感与地统计的森林生物量时空变异分析[J].北京林业大学学报,2016,38(2):10-19.
[17] 王立海,邢艳秋.基于人工神经网络的天然林生物量遥感估测[J].应用生态学报,2008,19(2):261-266.
[18] 张志,田昕,陈尔学,等.森林地上生物量估测方法研究综述[J].北京林业大学学报,2011,33(5):144-150.
[19] LU D, CHEN Q,WANG G, et al. Aboveground forest biomass estimation with landsat and lidar data and uncertainty analysis of the estimates[J]. International Journal of Forestry Research,2012(2):1-16.
[20] 袁野,李虎,刘玉峰.基于改进型BP神经网络的西天山云杉林生物量估算[J].福建师范大学学报(自然科学版),2011,27(2):124-132.
[21] CYBENKO G. Approximation by superpositions of a sigmoidal function[J]. Mathematics of Control Signals & Systems,1989,2(4):303-314.
[22] 车少辉,张建国,段爱国,等.杉木人工林胸径生长神经网络建模研究[J].西北农林科技大学学报(自然科学版),2012,40(3):84-92.
[23] 国庆喜,张锋.基于遥感信息估测森林的生物量[J].东北林业大学学报,2003,31(2):13-16.
[24] 翟晓江,郝红科,麻坤,等.基于TM的陕北黄龙山森林生物量模型[J].西北林学院学报,2014,29(1):41-45.
[25] 刘琼阁,彭道黎,涂云燕,等.基于偏最小二乘的森林生物量遥感估测[J].东北林业大学学报,2014,42(7):44-47.
[26] 蒋云姣,胡曼,李明阳,等.县域尺度森林地上生物量遥感估测方法研究[J].西南林业大学学报,2015,35(6):53-59.
[27] 范文义,张海玉,于颖,等.三种森林生物量估测模型的比较分析[J].植物生态学报,2011,35(4):402-410.
[29] 马泽清,刘琪璟,徐雯佳,等.基于TM遥感影像的湿地松林生物量研究[J].自然资源学报,2008,23(3):467-478.
[30] 李明诗,谭莹,潘洁,等.结合光谱、纹理及地形特征的森林生物量建模研究[J].遥感信息,2006(6):6-9.
[32] 王轶夫, 孙玉军, 郭孝玉. 基于BP神经网络的马尾松立木生物量模型研究[J].北京林业大学学报,2013,35(2):17-21.

