挖深式消力池深度的显式试算法

韩玖龙 ，孙 鹏 ，张志昌

（1.陕西省镇坪县水利局，陕西 镇坪，725600；2.西安景天水利水电勘测设计咨询有限公司，陕西 西安710016；3.西安理工大学，陕西 西安710048）

0 前言

底流消力池有三种形式，即挖深式消力池、消力坎式消力池和综合式消力池。其中挖深式消力池的深度相对于消力坎式消力池坎高的水力计算更为复杂。

挖深式消力池水力计算的主要任务是确定消力池的深度和消力池的长度。对于消力池的长度已有许多经验公式，本文不予讨论。对于消力池的深度，我国的水力学教科书[1][2]以及水利行业标准上均采用试算法[3-4]。该方法理论上成熟，方法上可靠，精度高，缺点是试算比较麻烦。所以许多学者试图对其进行简化计算。早在1938年，前苏联的A.A乌根秋斯就对挖深式消力池做了简化计算，他将试算法转化为乌根秋斯曲线图[5]，实际上就是图解法。乌根秋斯的图解法存在较大的误差，笔者根据乌根秋斯图解法的习题，用试算法求得的值比乌根秋斯曲线相差了32%。张志昌根据消力池深度计算的基本公式，通过分析给出了消力池深度的迭代计算方法[6]，该方法计算简单，精度与试算法完全一致。Husain给出了一个计算消力池深度的简单方法[7]，文献[6]的验证结果表明，该方法与试算法相差26.4%。Forster也给出了一个简化计算公式[8]，该公式将消力池相对深度d/hc1化为跃前断面弗劳德数Fr1的函数，公式看似简单，但由于跃前断面弗劳德数Fr1与消力池深度有关，所以计算时仍需试算，且计算精度很差，文献[6]的验证结果表明，该公式与传统试算法甚至相差了62%。黄朝煊研究了消力池最不利条件下池深的极值[9]，给出了跃后相对水深与相对单宽流量的经验公式，公式是假设一个消力池深度，求出跃前断面的总水头，然后直接求解跃后水深，但由于消力池深度隐含在公式中，所以仍需要试算才能确定消力池深度。倪汉根在击波、水跃、跌水、消能一书中介绍了Hager等计算消力池深度的新方法[10]，Hager等称这种方法为阶控水跃，有三种计算方法。阶控水跃在计算时需先确定水跃长度、水体的重量修正系数和跃后断面的动水压力修正系数。在计算消力池深度时，仍要先假设一个消力池深度d，然后依次计算跃前水深hc1、跃前断面的弗劳德数Fr1、动水压力修正系数、水跃长度Lj、水跃共轭水深比h2/hc1，将计算的水跃共轭水深比h2/hc1和下游水深ht与跃前水深hc1的比值ht/hc1相比较，如果ht/hc1>h2/hc1，水跃已经淹没，只要淹没系数σj在合理的范围内，消力池深度d即为所求，如不在合理的范围内，则需重新假设消力池深度d，重复上面的计算过程，直到达到所需的精度为止。Hager等计算消力池深度的过程十分繁琐，但其优点是只要先假设一个消力池深度d，以后的计算均为显式计算，不需要试算，也不需要迭代。阶控水跃计算消力池的深度与传统的试算法有一定的差距，Hager等自己提出的三种计算方法的计算结果也差距较大，例如文献[10]给出的例题中，一种计算方法得到水跃的共轭水深比为3.26，另一种算法则为3.68，相差了11.4%，可见用阶控水跃计算消力池深度的方法还值得进一步商榷。

1 显式计算方法

挖深式消力池如图1所示。图中0-0线为原河床地面线，0'-0'线为挖深后的护坦底面线。当池中形成淹没水跃后，水流出池时，其水流现象类似于宽顶堰的水流现象，水面跌落高度为Δz，然后与下面水面相衔接。

图1 挖深式消力池剖面图

未设消力池时，设原河床以上总水头为E0，收缩断面水深为hc，溢流坝的流速系数为，溢流面的单宽流量为q，写上游水库与收缩断面的能量方程得

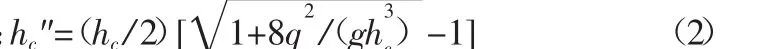
跃后共轭水深为设消力池后，设消力池的深度为d，以消力池底板算起的上游总水头为T0，收缩断面水深为hc1，则：

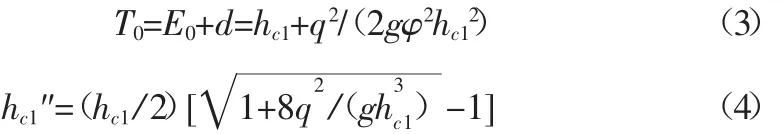
由图 1的几何关系可得：hT=σ1hc1"=d+ht+Δz （5）

式中，ht为下游水深；为水面跌落高度，其计算式为：

式中，φ'为消力池的流速系数。

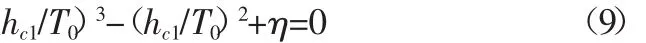
对上式求导数并令其为零，求得0≤hc1/T0≤2/3，代入上式得η的取值范围0≤η≤0.14815。

公式（9）为一元三次方程。一元三次方程的传统解法为卡丹公式。近年来我国学者范盛金提出了一元三次方程的简化计算方法，称为盛金公式[11]，盛金公式比卡丹公式在判别式的选择和计算方面都要简单。

本文用盛金公式对式（9）求解得：

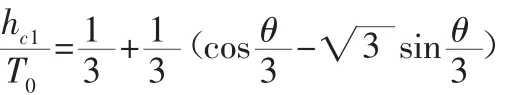
式中，θ=arccos（-1+27η/2）。

因为，代入式（4）并将公式无因次化得：

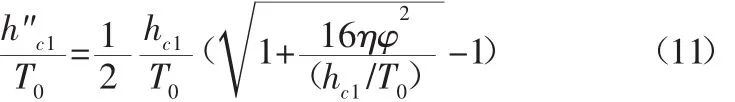
式（11）即为计算跃后断面相对水深的计算公式。

将式（6）代入式（5）整理得：

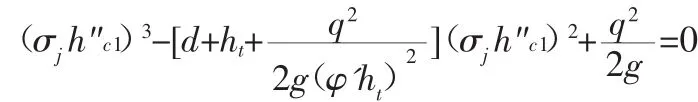
对上式无因次化得：

令k=d+ht+q2/[2g（φ'ht）2]/（σjT0）代入式

（12）得：（h"c1/T0）3-k（h"c1/T0）2+λ=0 （13）

对上式求导数，并令其等于零得：

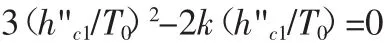
对上式求解得 0≤（h"c1/T0）≤2k/3，代入式（13）得 0≤λ≤4k3/27。

由式（13）可以看出，一元三次方程的系数 a=1、、c=0、d=λ，根据盛金公式求解公式（13），其判断式为：

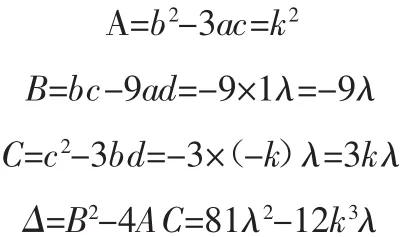
将0≤λ≤4k3/27代入上式判断，在λ=0和λ=4k3/27时，Δ=B2-4AC=0，这两种极端情况一般很少发生。当0＜λ＜4k3/27时，Δ=B2-4AC=81λ-12k3λ＜0。所以公式（13）的解为：

式中，α=arccos[-1+27λ/（2k3）]。

令公式（11）和公式（14）相等得：

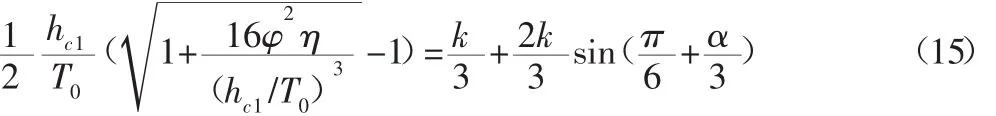
公式（15）看似简单，实际上 η、k、α均含有消力池深度 d、是一个隐函数关系式，无法直接求出d。但在计算中只要假设一个d，就可以依次求出 η、θ、k、λ、α，再由公式（10）求出 hc1/T0，由公式（11）求 h"c1/T0，由公式（14）求出另一个 h"c1/T0，如果公式（11）和公式（14）求得的h"c1/T0相等，消力池深度d即为所求。以上计算过程均为显式计算，即显式试算法，较传统试算法计算公式简单、计算过程方便。

2 显式试算法应用举例

某溢流坝为WES剖面，坝顶部设闸门控制流量。已知坝顶部水头H=3.2 m，下泄的单宽流量q=6 m3/（s·m），相应的下游水深ht=3.05 m。已知坝高P=P1=10 m，溢流坝的流速系数φ=0.90，消力池的流速系数φ'=0.95，试判断是否需要修建消力池，若需设置消力池，试设计一降低护坦式消力池，求消力池的深度d。

计算步骤：

1）判别坝下游水跃的衔接形式

因为下游坝高P1=10m＞1.33H=1.33×3.2=4.26m，为高坝，可不计行近流速水头，即取H0=H=3.2m。

2）判断是否需要修建消力池：

因为hc

"=3.9709＞ht=3.05，所以需要修建消力池。

3）消力池深度的计算

首先估算消力池的深度。消力池深度的估算公式是从式（5）得来的，假设不考虑消力池后的水面降落，则消力池的估算深度为：

已知下游水深为ht=3.05m，所以第一次试算的消力池深度为：

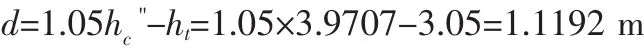
下面求消力池的深度。假设 d=1.12m，求参数 T01、η、θ、κ、λ、α：

η=q2/（2gφ2T301）=62/（2×9.8×0.92×14.323）=7.72205×10-4由公式（11）求得：

由公式（11）求得 h"c1/T01：

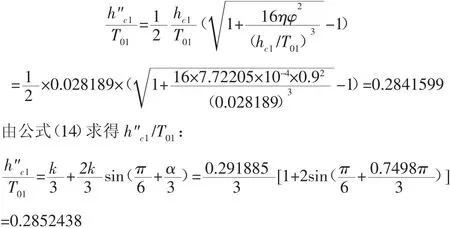
可以看出，公式（11）和公式（14）求得的值不相等，需重新假设d，重复上面的计算过程。现列表计算。在计算时用Excel列表，表中 q、E0、φ、σj、φ'、ht为已知值。再在表中列入需要计算的值 T0、η、θ、hc1/T01、h"c1/T01、k、λ 和 α 和的计算公式。计算时只改变一个参数就是消力池深度d，然后用鼠标下拉，即可得到计算值。

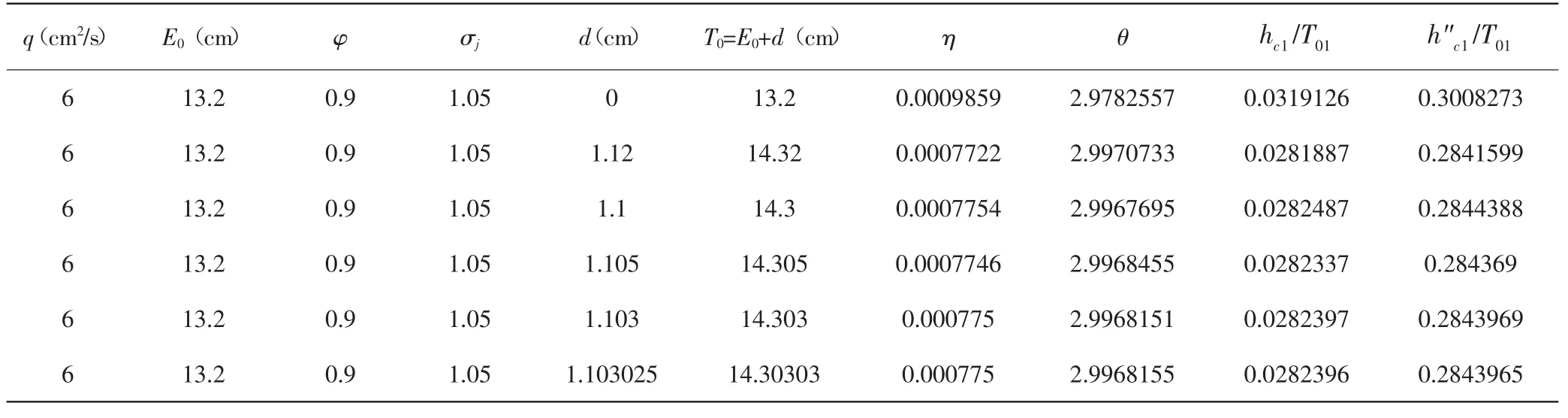
表1 用公式（11）计算跃后水深表

表2 用公式（14）计算跃后水深表

对比表1和表2可以看出，当d=1.103025m时，表1和表2计算的值相同，所以取d≈1.103m即为消力池深度。此算法与试算法的计算结果完全相同，但计算过程均为显式计算，比试算法简单的多。

3 结语

消力池深度传统试算法的优点是公式物理意义明确，计算精度高。缺点是消力池的跃前断面水深在计算过程中为隐函数关系式，每假设一个消力池深度，都需通过试算或迭代计算求得跃前断面水深，然后才利用其他公式求消力池的深度，计算过程比较复杂。Hager提出了消力池深度的阶控水跃算法，其优点是计算中先假设一个消力池深度，以后的计算均为显式计算，克服了试算的困难，缺点是计算过程中需先确定水跃长度、水体的重量修正系数和跃后断面的动水压力修正系数，然后才能计算消力池的深度，计算公式多，计算过程较繁。本文受Hager阶控水跃计算方法的启发，从计算消力池深度的基本公式出发，利用范盛金求解一元三次方程的方法，给出了计算跃前断面水深的显式计算公式，从而实现了计算消力池深度的显式试算法，此试算法比传统试算法和Hager阶控水跃算法简单、方便。

[1]张志昌.水力学（下册）[M].北京：中国水利水电出版社.2011:198-203.Zhang Z C.Hydraulics(two volumes)[M].Beijing:China Water Power Press,2011:198-203.(in Chinese)

[2]吴持恭.水力学(下册)[M]北京：高等教育出版社，2006:9-14.Wu Chi-gong.Hydraulics（two volumes）[M].Beijing:Higher Education Press.2006:9-14.(In Chinese)

[3]李启业，郭竟章，夏毓常.等.SL253-2000中华人民共和国行业标准.溢洪道设计规范[S].北京：中国水利水电出版社.2000：58～60.Liqiye，guo jingzhang，xia yuchang.etal.SL253-2000.industry standard of the People's Republic of China Design code for spillway[S].Beijing:ChinaWater Power Press.2000：58～60.(in Chinese)

[4]陈登毅，张平易，徐宗喜.等.SL265-2001.中华人民共和国行业标准.水闸设计规范[M].北京：中国水利水电出版社.2001：56～57.Chen dengyi，zhang yiping，xu zongxi.et al.SL265-2001.industry standard of the People'sRepublic ofChina.Design specification for sluice[M].Beijing:ChinaWater Power Press.2001：56～57.(in Chinese)

[5]基谢列夫.水力学计算手册 [M].北京：电力工业出版社,1957:352-354.Кислев.Handbook ofHydraulic Calculations[M].Beijing:ElectricPower Industry Press,1957:352-354.(in Chinese)

[6]张志昌，李若冰.基于动量方程的挖深式消力池深度的计算[J].西北农林科技大学学报（自然科学版），2012，40（12）：214-218.Zhang zhichang，Li ruobin.Calculation on the depth of deepened-stilling basin based o n momentum equation [J].Journal of Northwest A＆F University（Nat.Sci.Ed.）2012，40（12）：214-218.

[7]Husain D.Alhamid A A,Negm A A M.length and depth of hydraulic jump in sloping channels[J].Journal of Hydraulic Research,1994(6):899-910.

[8]Forster JW，Skrinde R A.Control of the hydraulic jump by sills[J].American SocietyofCivilEngineers，1950，115：973-987

[9]黄朝煊，王贺瑶，王正中，赵延风.消力池最不利条件下池深极值探讨[J].水力发电学报，2015，34（1）：79-84.Huang chaoxuan Wang heyao Wang zhengzhong Zhao yanfeng.Investigation of extremum depth of sluice stilling basin under the most unfavorable conditions[J]Journal of hydroelectric engineering,2015，34（1）：79-84.

[10]倪汉根，刘亚坤.击波、水跃、跌水、消能[M].大连：大连理工大学出版社，2008：134～234.Ni Hangen,Liu Yakun.Shock wave,Hydraulic jump,Plunge,Energy dissipation [M].Dalian：Dalian University of Technology Press，2008：134～234.(in Chinese)

[11]范盛金.一元三次方程的新求根公式与判别法[J].海南师范学院学报（自然科学版），1989，2（2）：91-98.Fan shengjin Anew extracting formula and a new distinguishingmeans on theone variable cubic equation[J].Naturalscience J ournalofHainan teacherscollege1989，2（2）：91-98.