基于离散元方法的某边坡变形分析

窦 灿

（中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014）

离散单元法由Cundall于1971年[1]提出的一种专门用于解决不连续介质问题的数值方法。岩体是多裂隙介质[2]，被各种结构面所切割，特别是在开挖区域的附近，岩石破碎及大变形往往明显呈不连续的性质[3]。由于离散元方法既能模拟接触面的大变形，又能模拟块体内部的连续变形，适用于模拟被节理、断层等构造面切割而成的不连续岩体介质，是分析不连续岩体的一种较理想的数值计算方法[4]。

三维离散元软件3DEC采用基于非连续介质力学理论的离散元方法求解[5]，本文基于3DEC，研究了某电站左岸边坡开挖过程中变形规律，并着重研究软弱结构面对边坡变形的影响。

1 离散元理论及计算软件

通常岩体被认为是各种离散块体组成的，块体之间的相互作用力根据位移和力的关系式来求解，单个块体的运动遵循牛顿运动定律，就是力和力矩的平衡，因离散元块体之间是彼此互不约束的，块体之间不存在变形协调的约束，需要满足的是物理方程和运动方程[2]。

（1）物理方程

式中，Fn为块体之间力的法向分力；kn为法向刚度系数；Fs将为块体之间力的法向分力；ks为接触面的剪切刚度系数。

（2）运动方程

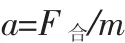
式中，a为加速度，m为岩块质量。在分别对X方向和Y方向然后分别进行向前差分的数值积分，可以得到岩块X方向和Y方向的速度和位移:

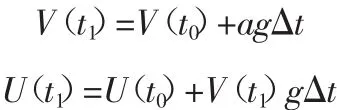
式中，V（t1）为时间的速度，U（t1）为时间的位移，t0为起始时间，Δt为时间步长。计算时依据时步迭代，并遍历每个块体，直到每个块体不再出现不平衡力和不平衡力矩为止。

2 计算模型

2.1 基本地质条件

某电站左岸边坡赋存环境复杂，地应力水平较高，坝头部位边坡岩体条件较差，并发育有f5、f8、f42-9、f2等不同规模的断层，其中f5、f8断层陡倾坡外，f42-9断层缓倾坡外，走向近SN的SL44-1等深部裂缝、岩脉(X)、高高程砂板岩中和中低高程T2-3z2(6)层大理岩中发育的层间挤压错动带，故需侧重研究软弱结构面对边坡变形的影响。

为充分考虑开挖坡体的地质代表性，选取II1-II1为计算剖面，该剖面可以用来分析左岸边坡拉裂变形体的后缘拉裂面岩脉(X)和断层f42-9的变形，以及研究深部裂缝在开挖卸荷作用下变形的发展过程。同时还可以充分考虑开挖坡体，II1-II1的工程地质剖面如图1所示。

图1 II1-II1剖面工程地质剖面图

2.2 左岸边坡的离散元分析

针对左岸边坡，分别建立局部及真实三维模型对边坡开挖过程中的变形进行分析。参考前期勘察阶段大量的试验工作，同时参照坝基岩体质量分级建议值进行取值。计算中块体采用Mohr-Coulomb塑性本构关系，结构面采用面接触库仑滑移模型。岩体及结构面力学参数如表1及表2所示。

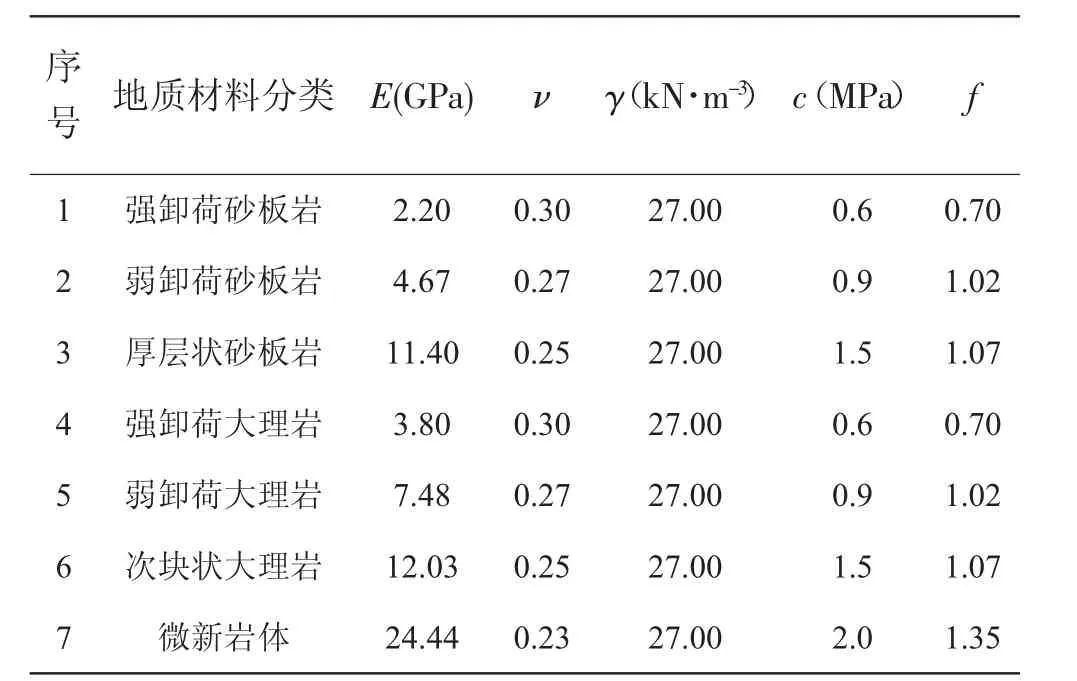
表1 岩体参数取值表

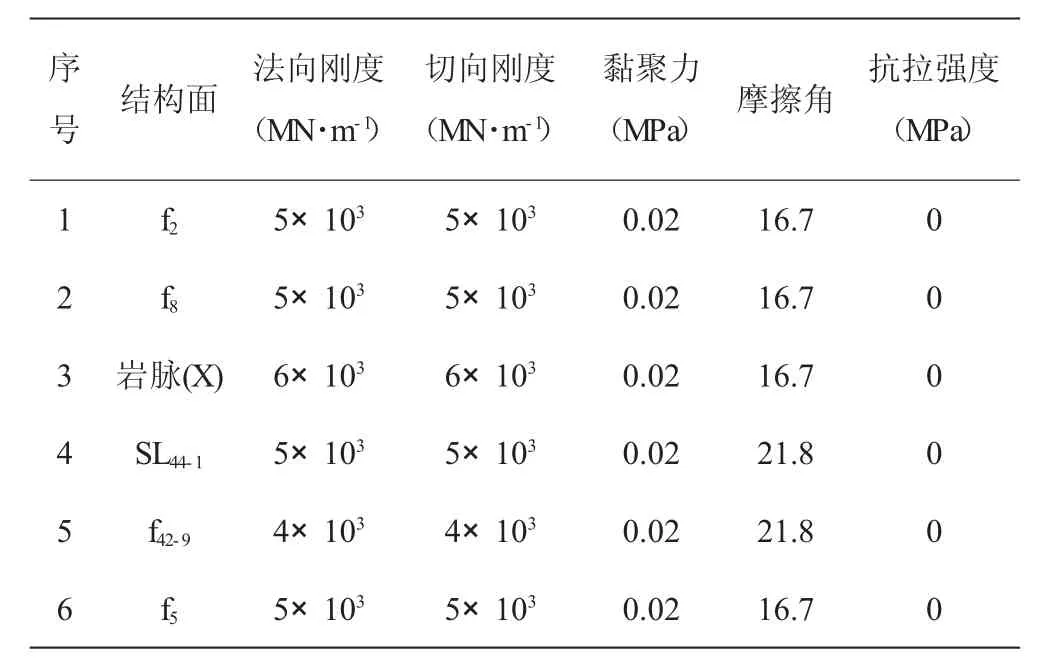
表2 结构面参数取值表

2.2.1 局部三维模型分析

左岸拱肩槽边坡II1-II1剖面方位为NE28°。坐标系X轴方向为NE28°；Z方向以铅直向上为正。模型的范围为：横河向方向取1250m，竖直方向则从高程1320m到高程2820m，模型沿河流方向取值30m。计算模型的底部用固定约束，左右两侧采用法向约束，整个计算域共建立了331个块体，剖分了31578个单元，顶点个数13145，接触个数1462，子接触个数4979。

开挖后边坡形态见图2，分步开挖体形态见图3。模型中考虑的控制性结构面包括断层 f2，f5，f8，f42-9，以及岩脉(X)和深部裂缝SL44-1。拟通过边坡的分步开挖、分期支护来模拟边坡施工期的工作状态。

图2 开挖完成后边坡形态

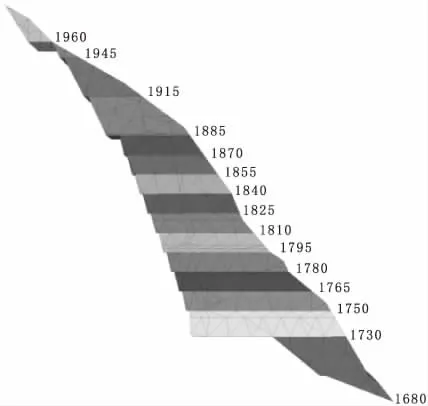
图3 开挖步模拟图

（1）边坡整体变形分析

边坡在开挖过程中，当开挖至高程1825m时，边坡开挖面主要是竖向位移为主，表现为边坡开挖面在上覆岩体挖除后的回弹变形，竖直向回弹位移最大值为43.7mm，拉裂变形体底滑面出现最大值约为25mm。而方边坡开挖至1795m时，随着阻滑岩体的全部挖除，拉裂变形体的位移显著增大，横河向最大位移达57 mm，竖直向向下位移量值最大约为27 mm，呈现出横河向位移起控制作用的特点。

边坡在开挖完成后的横河向及竖直向位移云图见图4、图5，横河向位移最大值出现在拉裂变形体剪出口处，量值约为64mm，回弹位移最大值约为37mm，出现在新开挖面上。

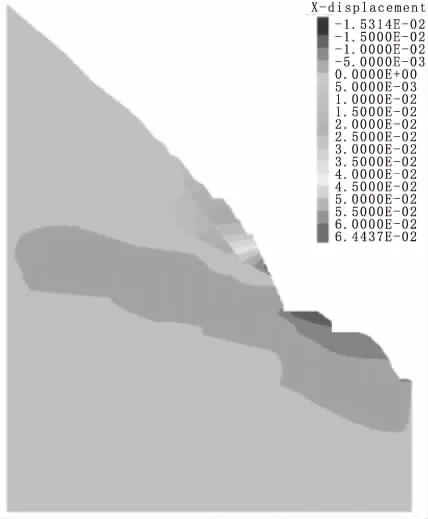
图4 横河向位移云图（开挖至1680 m）

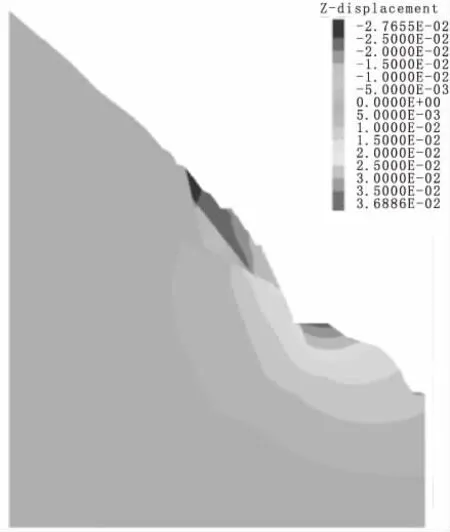
图5 竖直向位移云图（开挖至1680 m）

（2）结构面剪切变形

结构面剪切位移情况见图7，边坡在开挖过程中，初期多是沿岩脉剪切滑移，在拉裂变形体的阻滑岩体被挖除后，沿断层f42-9的位移陡然增大，其剪切位移在开挖至1810m时，约为33mm。在开挖至1795m时，其变形控制的拉裂变形体位移已显著增大，其剪切滑移变形可达74mm。由此可以看出拉裂变形体沿横河向变形主要受断层f42-9控制。

（3）结构面法向变形

图6 模型中考虑的结构面

图7 结构面剪切位移图（开挖至1680 m）

结构面的法向变形量值较剪切变形较小，本处对其中的典型的开挖时步进行分析。边坡开挖至高程1885m、高程1795m时的法向位移矢量图见图8和图9。

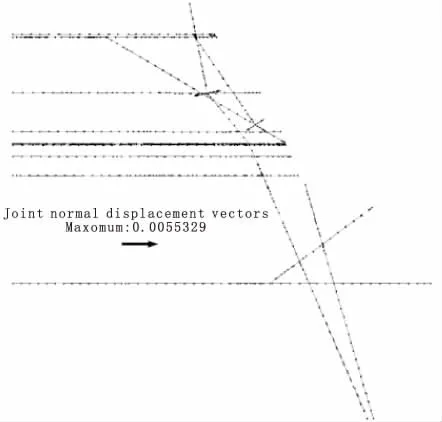
图8 开挖至高程1795 m时结构面法向位移矢量图

当开挖至高程1795m时，岩脉走向转折处法向变形较大，量值约为5mm，拉裂变形体的底滑面f42-9在与深部裂缝SL44-1相交处法向变形约为3mm，结构面变形呈现出张开的特征。边坡开挖至高程1680m时，结构面法向变形变化不大。

图9 开挖至高程1680时结构面法向位移矢量图

（4）锚索变形分析

数值模型中采用了预应力锚索对边坡进行了加固，锚索间距设置为44m，矩形布置，下倾角取为8度，锚索长度为60，80m，采用交替布置，施加预应力2000 kN。数值模型中锚索设置的原则是下一级边坡开挖后，锚索加固上一级边坡。锚索参数取值如表3。

表3 锚索参数取值表

图10为锚索在开挖完成后的变形图，其锚索横河向位移最大量值达48mm，其中位移大值与拉裂变形体的边界吻合，说明锚索在限制拉裂变形体的形变过程中发挥着积极的作用。

图10 锚索横河向位移放大图

为分析锚索施加对边坡位移场的影响，对比未加固边坡位移云图可知，开挖完成之后，拉裂变形体剪出口最大横河向位移约为66mm，相对实施锚索加固增加了2mm。

2.2.2 三维模型数值模拟

考虑到边坡的复杂地形及开挖体的三维效应，数值模拟中同时建立了左岸边坡的三维模型。模型中的软弱结构面则是主要考虑了岩脉(X)、断层f42-9、深部裂缝SL44-1等。

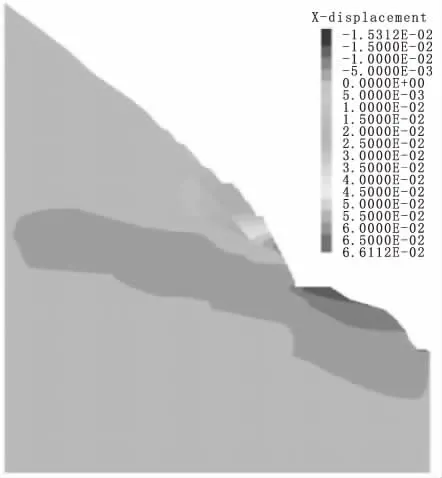
图11 未加锚索边坡位移云图（开挖至1680 m）

考虑到模型的复杂性和建模的可行性，在建立计算模型过程中对左岸边坡原地质模型进行了一定的简化。模型X轴正方向指向NE28°，Y轴指向NW62°，Z轴正方向竖直向上。为使模型具有相对的独立性，其计算范围为顺河向取600m，横河向770m, 垂直向取765m。计算模型共建立块体10823个，剖分单元315508个，节点196615个。

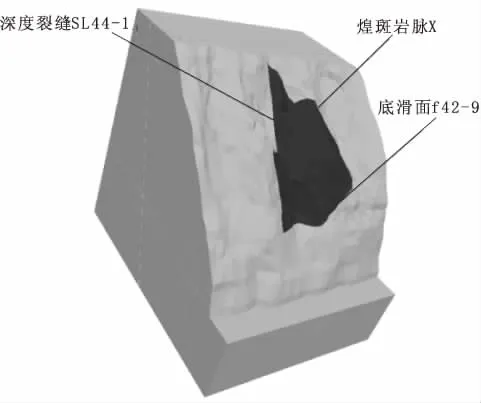
图12 拉裂变形体所处位置

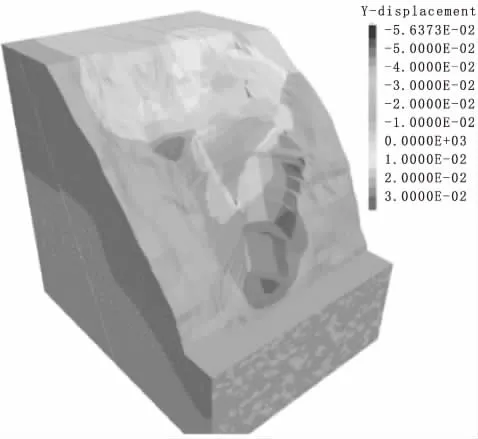
图13 边坡开挖完成后横河向位移云图

（1）数值模拟结果

三维数值模型对边坡逐级开挖及锚索加固进行了模拟，规律如下：边坡在开挖至高程1780m时，横河向位移显著增大，此时拉裂变形体阻滑岩体全部被挖除，断层f42-9与深部裂缝的交线被揭露，剪出口处出现最大横河向位移，其量值约为50mm。同时拉裂变形体边界处竖向位移呈现出下滑趋势，量值在18mm以内。边坡开挖完成后的横向位移云图见图13，最大横河向位移出现在拉裂变形体出口位置，量值约为58mm。

（2）锚索变形分析

边坡开挖完成，锚索横河向位移如下图14。锚索在拉裂变形体下滑影响下，亦产生了较为明显的横河向位移，最大量值约为36mm。图15为未加锚索边坡横向位移云图。三维数值模拟结果表明，边坡采取锚索进行加固后，边坡最大横河向位移较未加固横河向位移可减少4mm。

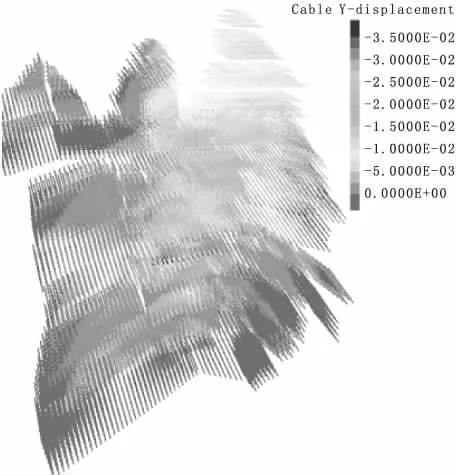
图14 边坡开挖完成后的锚索横河向位移云图

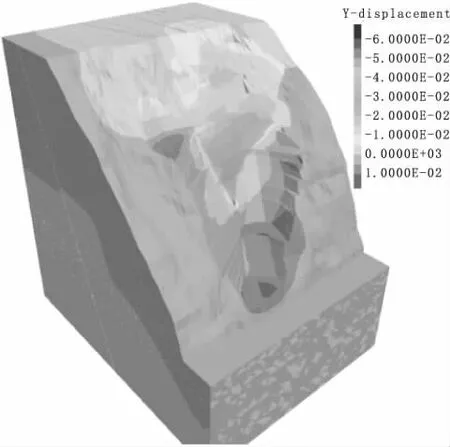
图15 边坡开挖完成后横河向位移云图（未加锚索）

3 结论

（1）通过建立边坡II1-II1剖面的局部三维模型，对边坡在开挖过程中的变形响应进行了分析。在对边坡开挖支护进行概化的基础上，共进行了15步开挖。计算结果表明，在边坡逐步开挖过程中，随着拉裂变形体外侧的阻滑岩体的不断挖除，其位移呈现加速增长的趋势，在拉裂变形体完全出露时，其最大横河向位移量值约为58 mm，由竖直向位移则可以看出其有整体下滑的趋势，竖直向下滑的位移最大量值约为27 mm。随着支护措施的逐步到位，在后需开挖过程，拉裂变形体整体位移变化不大，最终边坡开挖完成后，其横河向位移最大量值约为64mm。

（2）在对边坡位移进行分析的同时，还对边坡的结构面开挖过程中的变形进行了讨论。组成拉裂变形体的断层f42-9、深部裂缝SL44-1和岩脉(X)等结构面在边坡开挖过程中主要以剪切滑移为主，尤其是底滑面f42-9其剪切滑移量值最大约为74 mm，对拉裂变形体起着控制性的作用，结构面法向变形主要为张开变形，量值不大。

（3）在对比锚索的加固效果后发现，锚索在限制边坡变形方面发挥着积极的作用，施加锚索后的边坡其横河向位移量值较未加固边坡为小，最大量值减少约2mm，锚索在边坡开挖完成后，横河向变形值约为48mm。

（4）通过对真实三维模型分析后发现，边坡逐级开挖变形呈现出与局部三维开挖相同的规律，最终边坡开挖完成后，其横河向位移最大量值约为58mm，比局部三维模型略小，施加锚索后的边坡其横河向位移量值较未加固边坡为小，最大量值减少约4mm，锚索在边坡开挖完成后，横河向变形值约为36mm。分析认为这主要是因为三维模型更能反映出侧向岩体的对拉裂变形体的限制作用。

[1]Cundall P A.A computer model for simulating progressive large scale movements in blocky rock systems[J].Proceedings of the International Symposium Rock Fracture,1971:1～8..

[2]E.hoek andW bray.岩石边坡工程[M].北京:冶金工业出版社,1991.

[3]孙广忠.岩体结构力学[M].北京,科学出版社,1998.

[4]Cundall PA.Formulation of three-dimensionaldistinctelementmodel[J].International JournalofRock Mechanics,1988,25(3):107～115.

[5]ITASCA.Three-dimensional distinct element code:user’s guide[M].Minneapolis:Itasca ConsultingGroup,Inc,2004.