抗差修正在白水坑水库实时洪水预报中的应用

王旭滢 包为民 王玉丽 游 洋 钟 华

(1.河海大学 水文水资源学院,南京 210098;2.中国电建集团中南勘测设计研究院有限公司,长沙410014;3.江苏省水利厅水资源处,南京 210029;4.南京水利科学研究院,南京 210029)

洪涝灾害是威胁人类生命财产安全的十大隐患之一,随着社会经济规模的扩大与发展,提高防洪能力势在必行.修建水库是防洪防汛工程的典型措施之一,水库入库洪水的精确预报是水库优化调度、保证水库下游安全的重要前提,因此研究水库洪水预报方案意义重大.水库流域洪水预报不同于一般的流域预报,水库大坝的建设会改变天然水文规律,从而给预报带来一定的复杂性和挑战性.受到影响的水文要素有:库区下垫面特性、河道洪水波的演进、坝址流量的获取方式、水文资料序列的一致性发生变化等.加之洪水预报自身的不确定性、预报方法的选择等其它公共因素,使得入库洪水预报结果误差较大,可信度较低[1].这些不确定因素会反映在反推得到的入库流量中,从而对实时校正结果造成“污染”.

观测误差按照大小可以分为三类:小误差、粗差、极值误差,后两者对估值影响最为明显.传统误差修正方法的基础是最小二乘法,它要求误差呈正态分布,然而实际中误差分布是未知的,难以概述,这会造成估值的不准确.抗差方法在未知误差具体分布的情况下,针对实时校正结果中的“污染”,提出了误差“污染分布”的概念,利用等价权,构造出特定的目标函数,从而抵御粗差和极值误差对估值产生的影响[2].流量资料的抗差方法已在理想模型中得到验证[3],本文针对水库预报问题,结合流量资料的抗差方法,对水库洪水预报实时校正进行改进.

1 水文模型与实时校正方法

根据本文研究区域的水文气象条件,采用新安江模型作为其入库洪水预报模型.

新安江模型属于概念性模型,其计算流程如图1所示.模型最大特点是“三分”:分单元、分水源、分阶段.分单元即根据流域下垫面的空间分布差异性对其进行分块;分水源即径流分水源,分为地表径流、地下径流、壤中流,在汇流速度上地表径流＞壤中流＞地下径流;分阶段即汇流过程分为坡面汇流、河网汇流.马斯京根河道汇流演算是通过联立水量平衡方程和槽蓄方程得到的,已知入流过程,通过上一时段出流量推算出下一时段的出流[4].

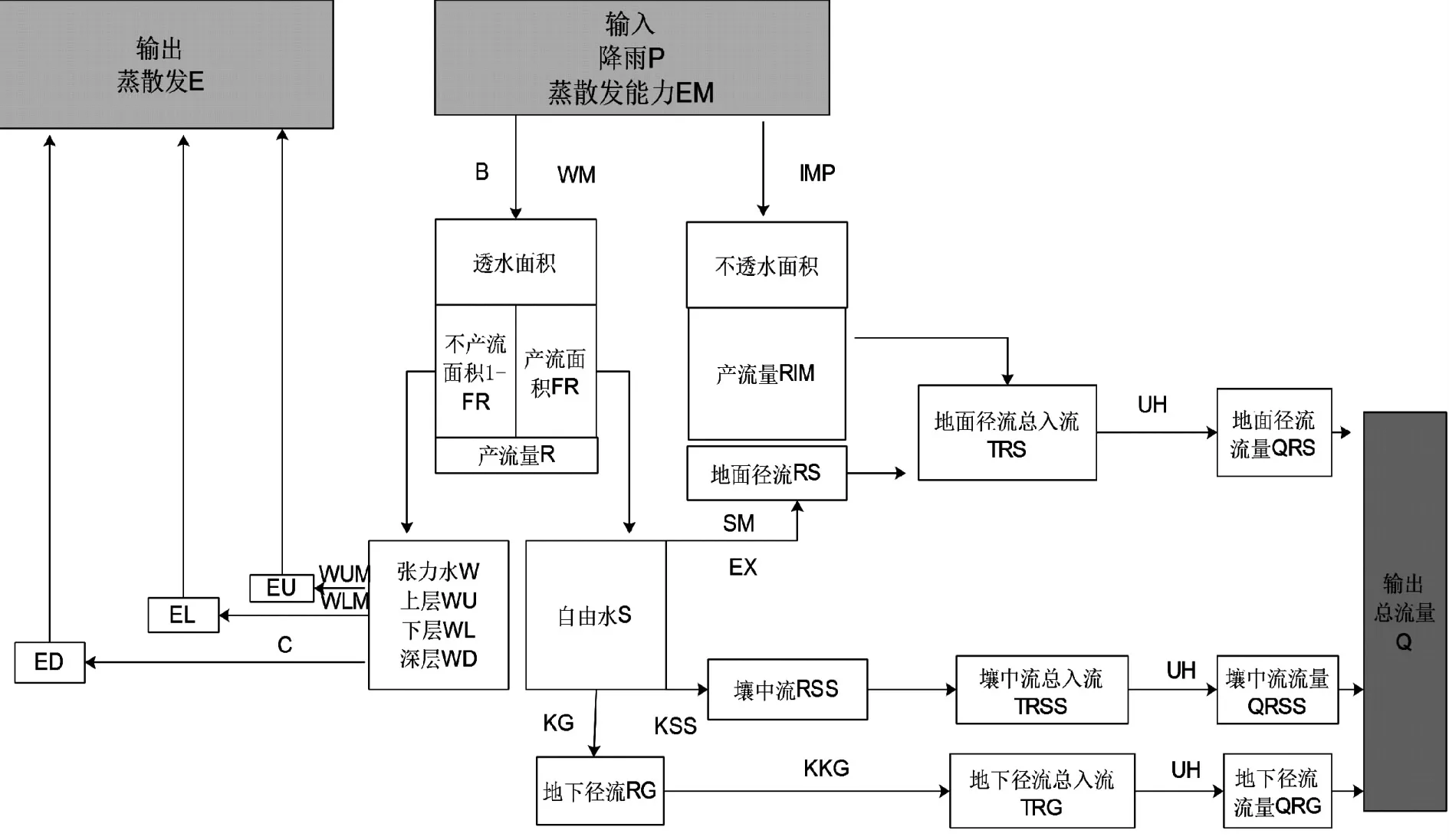
图1 三水源新安江模型计算流程图

洪水预报实时校正的对象可以是预报模型参数、预报误差以及状态变量等.常见的实时校正方法有自回归修正(AR模型)、递推最小二乘法、卡尔曼滤波等.这些方法能够实时处理预报系统中出现的误差,并且以这些误差作为修正的依据,在预报系统中作出及时的纠正反应[5].较为常用的是误差自回归修正法,即认为当前时刻的误差与此时刻之前的误差系列紧密相关,通过实测流量序列与预报流量序列建立残差序列,从而对残差进行实时校正,最后叠加到预报序列上.但该方法对自回归系数的估计是时不变的,而对于一个流域系统来说,实际应为时变非线性系统.因此,本文采用递推最小二乘法,根据实时输入的信息修正预报误差.

2 抗差修正方法

抗差修正来源于1960年Tukey[6]提出的两部分组合而成的污染分布:主体分布、污染分布.他认为主体分布是服从正态分布的,而污染分布则是极值误差和粗差聚集而成的,其分布无规律可循,难以用数学语言描述.Huber[7]通过把α邻域的分布函数转换为相应的极值函数ρ进行抗差估计.可以说,抗差估计是参数估计与非参数估计的结合,其目的就是削弱变方差对估值造成的不良影响.抗差估计的有效性主要取决于抗差权函数,目前常用的抗差估计方法有Huber法[7]、Tukey 双 权 法[6]、Hampel估 计[8]、IGG法[9].

对于水库流量修正,宜采用双权法的抗差权函数.由于入库流量反推带来粗差,流量过程线呈上下波动的锯齿状.为了将其修正成光滑的曲线,首先进行二次曲线拟合,对场次洪水实测值进行分段拟合处理得到光滑流量Qgh.二次曲线拟合的原则是最小二乘法,即最小平方法.分段的节点选择非常重要,关键是要结合计算流量的涨落特点来考虑[10].分段段数需尽可能多,否则会造成误差的增大.但是对于水库实测入库流量来说,资料信息较少,因此不能完全剔除某个实测值.但是为了限制异常值的影响,采用如下方法:建立降权区,在降权区内做抗差处理,之外则保留原信息[11].相较于理想模型中人为对粗差进行控制,实测信息中波动更为随机,规律性不明显,故要特别注意不能“抗错”和“抗过”.在保留实测有效信息的基础上,对残差较小的系列统一赋权重,只对残差较大系列进行抗差处理.因此,根据实测流量和光滑流量之间残差ζ(t)采用如下公式进行计算抗差权函数w(t)和权函数特征量:

为了最大可能保留有效实测信息,选择k=1.0.式(2)中m为数据点个数,可以认为数据点等权重,wi=1,因此每一场洪水σ为定值.

最终修正得到的流量即是光滑流量和实测流量按照权重进行分配,计算公式如下:

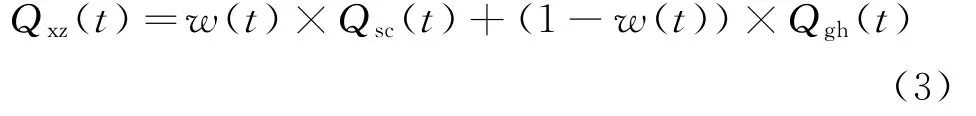
其中,Qsc(t)为实测流量,Qxz(t)为修正后的光滑抗差流量.

水库原入库实测流量过程线的波动大小可以用波动系数α表示.计算公式如下:

3 实例应用

3.1 流域概况

白水坑水库流域位于浙江省西南部江山港峡口水库上游,东经118°22'37″,北纬28°15'26″.白水坑水库的东边是本省的衢县、遂昌县,向南与福建省浦城县相邻,西与江西省玉山县、广丰县接壤,北靠本省的常山县.白水坑水库流域发源于浙闽赣三省交界的山区,地势南高北低.江山港是该流域的干流,属于钱塘江水系,江山港与常山港在衢州市双港口汇合后称为衢江.江山港主流两岸多山,少平原,河谷两岸多为山丘.山区的沉积物土质较薄,以砂砾质土为主.江山港属山溪性河流,洪水暴涨暴落,集流时间短.洪水的主要诱因是台风和梅雨,因此汛期在5～7月.洪水特征是峰高量大,呈“高胖”状.洪水过程一般历时3～4 d.白水坑流域属亚热带季风气候区,流域控制面积是330 km2.多年平均气温17.1℃左右,多年平均降水量1 754 mm,但分配不均,3～6月降雨占全年57%以上.

白水坑水库为江山港梯级开发的龙头水库,是集防洪、发电、灌溉、生态效益于一体的控制型大Ⅱ型水利枢纽.水库坝址位于大峦口乡雪花淤桥附近,距江山市区65 km,库区集雨面积330 km2,主流长26 km,多年平均径流总量4亿m3[13].

3.2 参数率定

选择白水坑水库流域2004～2009年日模资料以及21场次洪资料对新安江模型以及马斯京根流量演算参数进行率定,另外选择2010～2012年9场洪水进行验证.日模资料包括逐日蒸发、逐日降雨以及逐日入库流量,次洪模型资料包括次洪流量过程以及该场洪水所对应的降雨过程.参数率定的结果见表1.

表1 参数率定结果

率定期共有21场洪水,四项指标全部合格的共有21场洪水,合格率为100%.进一步分析模型模拟精度,将次洪模型实测径流深与计算径流深、实测洪峰流量与计算洪峰流量建立相关关系,如图2所示,点据均分布在45°线附近,相关关系良好.因此将此次率定的参数作为模型参数代入模型检验.

图2 相关关系图

经过检验期9场洪水的验证,均模拟合格,表明该套参数能够反映白水坑流域水文特性,可以作为预报参数.

3.3 抗差修正

选择2010～2012年波动强烈的8场洪水进行修正.具体步骤如下:首先采用分段二次曲线拟合得到光滑流量,每一段通过最小二乘法得到该段的拟合方程,得到连续的光滑流量过程线Qgh.其次利用式(1)、(2)计算抗差权重w(t)、权函数特征量σ,通过式(4)计算其波动系数α,估计其波动误差的影响情况.最终通过式(3)得到8场洪水的光滑抗差流量Qxz(t),将此作为实测流量来对预报流量进行实时校正.实时校正采用递推最小二乘法,计算修正后的残差从而得到计算模拟的校正值.

流量残差均方差从统计意义的角度反映了预报流量相对于实测值的偏离程度,但是原先未经抗差的实测流量存在着异常值的干扰.因此,采用流量残差抗差均方差来检验抗差效果,进一步计算残差减小率得到抗差的表现如何.计算公式如下:

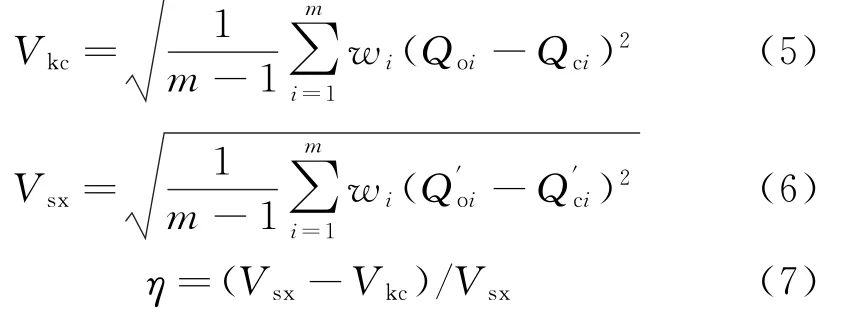
式中,Vkc为流量残差抗差均方差;Vsx为流量残差均方差;Qo、Qc分别为光滑抗差流量和抗差后实时校正的计算流量;Q'o,Q'c分别为不带抗差的实测值和其对应的实时校正计算值;η为残差减小率.

将其与抗差前、后的校正流量进行比较,分别计算其残差均方差,并计算残差减小率,结果见表2.

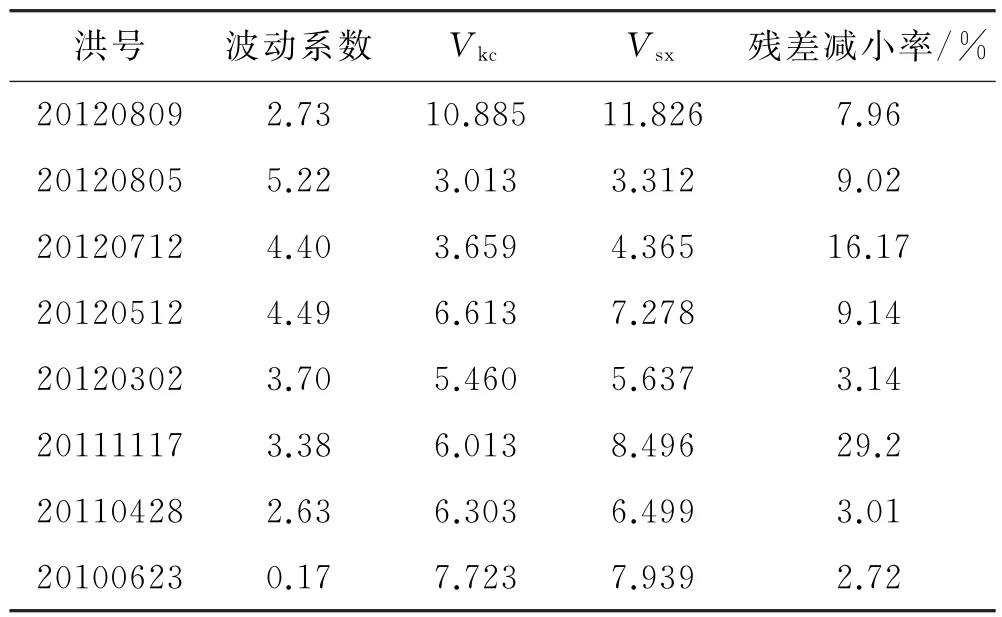
表2 抗差计算结果

以上结果表明,对8场历史洪水的实测流量抗差之后再进行校正,均能够有效减小残差,抵抗粗差、极值带来的不良影响,进而有效提高模拟精度.由于水库其调蓄特性,易出现陡涨陡落型洪水,波动系数较大,波动系数越大反映其产生粗差的概率越高.

4 结 论

本文采用新安江模型和马斯京根河道汇流模型对白水坑水库历史洪水进行模拟,率定相关参数,以水文站的实测流量以及历史雨情资料对新安江模型的参数进行率定和检验,得到适合该流域的一套参数优值,将其作为白水坑水库洪水预报方案中的默认参数值.针对入库洪水反推时造成的波动误差,利用抗差原理对8场“锯齿”状洪水进行修正之后再进行实时校正,以消除非正常因素对校正过程的不良影响.最终效果明显,可以消除大部分粗差,大大提高洪水预报精度.相较于其它修正方法,抗差计算过程简便,能够为水库预报系统提供较为准确的流量资料,可将其应用于水库实时预报系统中.

由于水库实时洪水的波动更为随机,因此,在建立抗差降权域、选择参值数时要着重考虑水库历史入库洪水出现粗差的频率以及幅度.目前抗差估计方法所针对的主要是线性估值问题,对于非线性函数的参数如何估计还需进一步研究.

[1] 李树平,张怀生.水库洪水预报误差分析[J].东北水利水电,2006,24(262):42-43.

[2] 包为民,嵇海祥,胡其美,等.抗差理论及在水文学中的应用[J].水科学进展,2003,14(4):428-432.

[3] 李佳佳,包为民,刘可新,等.流量资料抗差方法[J].水力发电,2016,42(4):27-30.

[4] 包为民.水文预报[M].3版.北京:中国水利水电出版社,2005.

[5] 田 雨,雷晓辉,蒋云钟,等.洪水预报实时校正技术研究综述[J].人民黄河,2011,33(3):25-26,28.

[6] Tukey J W.A Survey of Sampling from Contaminated Distribution in Contributions to Probability and Statistics[M].Stanford,Calif.:Stanford University Press,1960.

[7] Huber P J.Robust Estimation of a Location Parameter[J].Ann Math Statist,1964,35(1):73-101.

[8] Hampel F R.A General Qualitative Definition of Robustness[J].Ann Math Statist,1971,42(6):1887-1896.

[9] 周江文,黄幼才,杨元喜,等.抗差最小二乘法[M].武汉:华中理工大学出版社,1997.

[10]包为民,李荣容,王 涛,等.波动系数与洪水预报抗差效果关系分析[J].水力发电学报,2009,28(3):57-61.

[11]李荣容,吴国尧.水库入库流量抗差修正研究[J].中国农村水利水电,2008(11):12-14.

[12]Li Qian,Bao Weimin,et al.An Error Updating System for Real-time Flood Forecasting based on Robust Procedure[J].KSCE JOURNAL OF CIVIL ENGINEERING,2015,19(3):796-803.

[13]郭浩亮,吴士伟,姜新忠.白水坑水库泄洪洞设计[J].浙江水利科技,2006,143(1):56-58,77.