简单曲线回归分析及其应用

谷恒明，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

简单曲线回归分析及其应用

谷恒明1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

本文目的是介绍可以直线化的曲线回归分析相关内容及如何使用SAS软件来实现。一般来说，采用回归分析研究专业上确实存在联系的两个定量变量之间的依存关系。如果两定量变量之间是直线关系，那么直接采用直线回归分析即可；但在医学实验中，两定量变量之间的关系常常不是直线关系而是曲线关系，此时就应采用曲线回归分析。本文重点讲述可以直线化的曲线回归分析的种类及其SAS软件实现。

回归分析；曲线拟合；SAS软件；曲线直线化

*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

1 概 述

可直线化的曲线回归分析一般是通过变量变换的方法[1]，将原本是曲线关系的两个定量变量转化为直线关系，再对新变量进行简单线性回归分析得到直线回归方程，最后再回代到原始变量。此方法的关键是找到原始变量的合理变换方法，不恰当的变量变换只会产生错误的结果。

曲线回归分析的步骤：①在直角坐标系内绘制两个定量变量的散点图；②根据散点图全部散点的变化趋势，判断合适的曲线类型；③根据所选的曲线类型，进行变量变换，使变换后的两定量变量之间呈直线变化趋势；④对两个新变量建立直线回归方程，并作假设检验；⑤还原到初始变量，得到曲线回归方程；⑥若同一资料适合多种曲线类型，需要进行曲线拟合优度检验(当自变量只以一次项出现在回归方程中时，也可直接比较对整个回归方程所做的假设检验对应的F统计量，大者为优；也可看R2，大者为优)，比较其差异；⑦选择拟合最好的曲线回归方程，并从专业角度上判断其是否成立。

2 二项式曲线回归分析

当因变量与自变量不是简单的一阶关系，而是与自变量的二阶甚至高阶存在线性关系时，就需要使用多项式回归分析方法。本文介绍因变量与自变量的二阶存在线性关系的曲线拟合问题。散点图一般呈抛物线形状，因此，二次多项式曲线亦称二次抛物线。

【例1】研究某氧化酶活性与pH值之间的关系[2]，数据见表1。

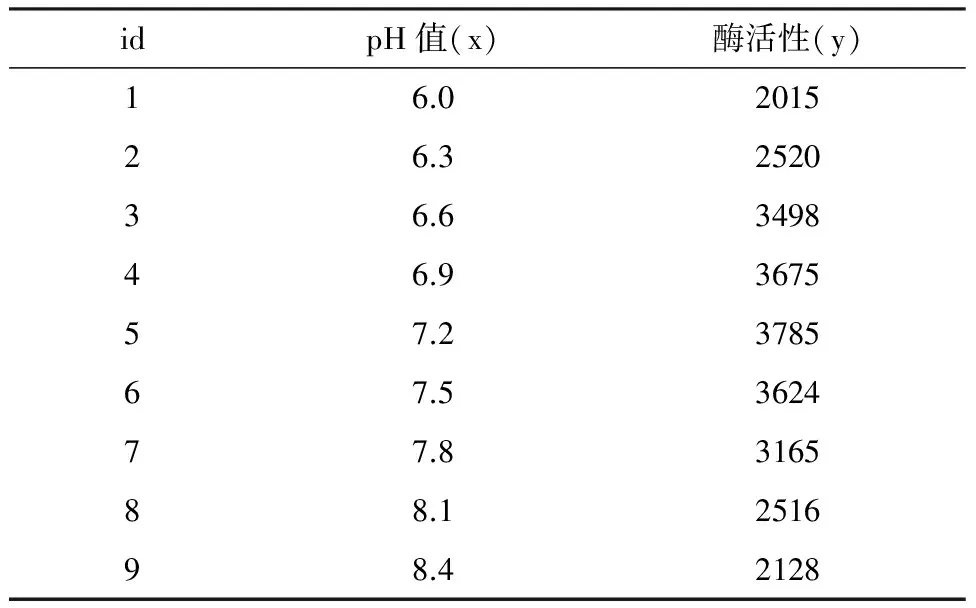
表1 酶活性(y)与pH值(x)数据

【分析与解答】试采用二次抛物线函数来拟合表1资料，其所需要的SAS程序如下：

data pwx; input id x y@@; x2=x*x; cards;

16．0201526．3252036．6349846．9367557．2378567．5362477．8316588．1251698．42128

;

run;

axis1label=('PH值(x)') order=(5.5 to 8.5 by 0.5);

axis2 label=(angle=90'(酶活性(y))') order=(1800 to 4000 by 200) minor=none offset=(0.5,0.5) major=(height=0.8);

symbolcolor=black interpol=join value=circle width=1.5;

proc gplot data=pwx;

plot y*x/haxis=axis1 vaxis=axis2;

run;

proc reg data=pwx; model y=x x2; run;

以上程序可分为三部分：第一部分创建临时SAS数据集；第二部分绘制散点图；第三部分构建二次抛物线回归方程并进行假设检验。散点图显示，两定量变量之间呈二次抛物线变化趋势。见图1。

图1 酶活性(y)与pH值(x)之间的散点图

对模型进行假设检验的结果见表2。

表2 方差分析

对模型中各参数进行估计和假设检验的结果见表3。

表3 参数估计

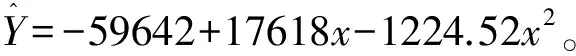
3 双曲线形式的曲线回归分析

当因变量与自变量的关系不是直线，而是曲线时，对变量进行适当变换，使曲线直线化。

【例2】资料来源于《中国卫生统计》的一篇文章，研究钩虫病患者治疗次数与复查阳性率之间的变化规律。见表4。

【分析与解答】在例1中，已给出绘制散点图的程序，读者自行修改即可，此处就不重复了。绘制的散点图见图2。

表4 钩虫病患者治疗次数(x)与复查阳性率(y)数据

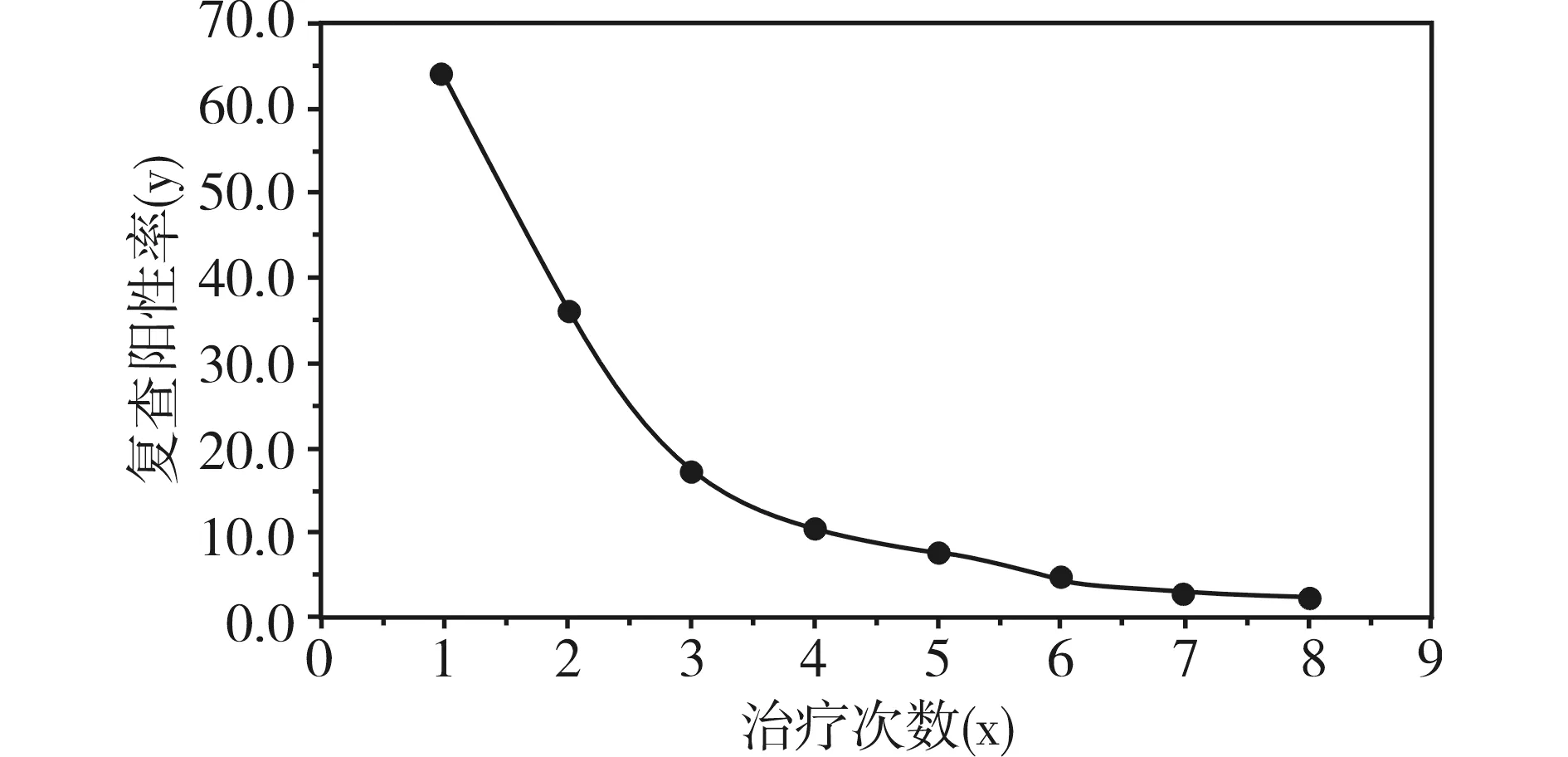
图2 钩虫病患者治疗次数(x)与复查阳性率(y)散点图

如图2所示，资料的散点图不呈直线变化，钩虫阳性率随着治疗次数越多阳性率越小，最后钩虫阳性率趋近于0。可以对自变量x进行倒数变换，重新拟合直线回归方程。

对自变量x进行倒数变换后的散点图(在例1中，已给出绘制散点图的程序，读者自行修改即可，此处就不重复了)见图3。

图3 钩虫病患者治疗次数的倒数(1/x)与复查阳性率(y)散点图

由图3可知，基本上实现了曲线直线化。接下来可以拟合双曲线回归方程。

所需的SAS程序如下：

data gouchong; input x y; x1=1/x; x2=log(x);

y1=log(y); cards;

163．9236．0317．1410．557．364．572．881．7

;

run;

proc reg data=gouchong; model y=x1; run;

由model语句可知，此处选择了对自变量进行倒数变换的方式。

此处省略了对模型进行假设检验的结果。参数估计结果见表5。

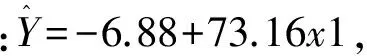
表5 参数估计

4 幂函数曲线回归分析

当因变量y随着x的变化符合幂函数曲线规律时，可以对自变量x和因变量y同时取对数变换，使幂函数曲线直线化。幂函数的一般形式为：

y=axb+k(a>0,x>0)

当不考虑k时，对等号两端同时取对数，

得：lny=lna+blnx，即lny与lnx之间呈直线关系。

【例3】沿用例2的资料，试拟合幂函数曲线回归方程。

【分析与解答】对因变量y和自变量x都进行对数变换后的散点图(在例1中，已给出绘制散点图的程序，读者自行修改即可，此处就不重复了)见图4。

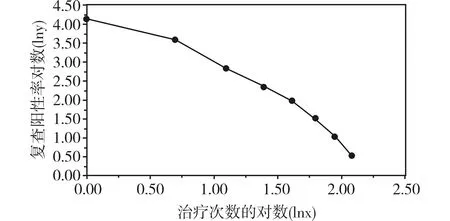
图4 钩虫病患者治疗次数的对数(lnx)与复查阳性率对数(lny)散点图

由图4可知，曲线直线化的效果较好。接下来可以拟合幂函数曲线回归方程。沿用前面的SAS数据步程序，现在所需要的SAS过程步程序如下：

Proc reg data=gouchong; model y1=x2; run;

由model语句可知，此处选择了对因变量和自变量都进行对数变换的方式。

表6 参数估计

5 指数函数曲线回归分析

当因变量y随着x的变化符合指数函数曲线规律时，可以对因变量y取对数变换，使指数曲线直线化。指数函数的一般形式为：

y=aebx+k或y=aexp(bx)+k

在不考虑k时，等号两端同时取对数，得：

lny=lna+bx

如果以lny与x在直角坐标系内绘制的散点图呈直线变化趋势时，就可以考虑采用指数函数曲线来拟合和解释y与x之间的关系。

【例4】沿用例2的资料，试拟合指数函数曲线回归方程。

【分析与解答】对因变量y进行对数变换后的散点图(在例1中，已给出绘制散点图的程序，读者自行修改即可，此处就不重复了)见图5。

图5 钩虫病患者治疗次数(x)与复查阳性率对数(lny)散点图

由图5可知，曲线直线化的效果较好。接下来可以拟合指数函数曲线回归方程。

沿用前面的SAS数据步程序，现在所需要的SAS过程步程序如下：

Proc reg data=gouchong; model y1=x; run;

由model语句可知，此处选择了对因变量进行对数变换的方式。

参数估计结果见表7。

表7 参数估计

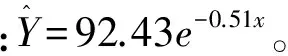
6 对数函数曲线回归分析

当因变量y随着x的变化符合对数函数曲线规律时，可以对自变量x取对数变换，使对数函数曲线直线化。对数函数的一般形式为：

y=alnx+k

如果以y和lnx在直角坐标系内绘制的散点图呈直线变化趋势时，就可以考虑采用对数曲线来拟合和解释y与x之间的关系。

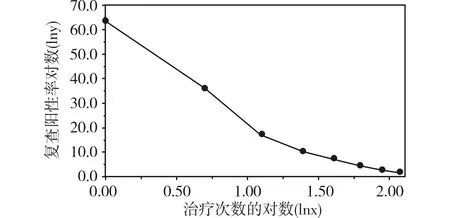
图6 钩虫病患者治疗次数对数(lnx)与复查阳性率(y)散点图

【例5】沿用例2的资料，试拟合对数函数曲线回归方程。

【分析与解答】对自变量x进行对数变换后的散点图(在例1中，已给出绘制散点图的程序，读者自行修改即可，此处就不重复了)见图6。

由图6可知，基本上实现了曲线直线化。接下来可以拟合对数函数曲线回归方程。

沿用前面的SAS数据步程序，现在所需要的SAS过程步程序如下：

Proc reg data=gouchong; model y=x2; run;

由model语句可知，此处选择了对自变量进行对数变换的方式。

表8 参数估计

对模型检验结果F=99.45，P<0.0001，说明所建立的回归模型有统计学意义，表格略。调整R2=0.9336，由表8参数估计结果可得曲线回归方程为：y=57.60-29.89x2，还原到原始变量，得到曲线回归方程为：y=57.60-29.89lnx

小结：由本文后四种曲线回归分析可知，有时一组数据可以通过多种变量变换方式得到直线回归方程，此时需要根据各种不同方法拟合的效果来得出最优的变换方式。本文中，指数函数的调整R2=0.9914，是四种曲线类型中最大的，因此应该选择指数函数曲线来进行曲线拟合为宜。

[1] 胡良平.科研设计与统计分析[M].北京: 军事医学科学出版社, 2012: 401-426.

[2] 徐天和, 柳青.中国医学统计百科全书 多元统计分册[M].北京: 人民卫生出版社, 2004: 147-149.

[3] 徐勇勇,陈长生,张成岗,等.曲线拟合中的几个问题[J].中国卫生统计,1994,11(2): 58-60.

Simplecurveregressionanalysisanditsapplication

GuHengming1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China

The paper is to introduce how to fit a curve regression equation by the variable transformation and how to perform it by using SAS software. In general, the regression analysis should be applied when there is the relationship between two quantitative variables in profession. If the two variables are linear, then the linear regression analysis can be used directly. However, in medical experiments, the relationship between the two quantitative variables is often not linear, so it is necessary to use curve regression analysis. This article focuses on fitting curve by variable transformation and the corresponding SAS software operation.

Regression analysis; Curve fitting; SAS software; Curve linearization

国家高技术研究发展计划课题资助(2015AA020102)

R195.1

A

10.11886/j.issn.1007-3256.2017.06.003

2017-12-03)

陈 霞)