简单线性回归分析及其应用

谷恒明，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

简单线性回归分析及其应用

谷恒明1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

本文目的是介绍简单线性回归分析的前提条件、种类、实现计算的SAS程序及结果解释，并说明数据是否值得做直线回归分析以及如何选择正确的直线回归分析类型。简单线性回归分析有三种具体情形，分别是：简单直线回归分析、加权直线回归分析和具有重复试验的直线回归分析。进一步通过实例来阐述如何进行不同的简单线性回归分析，并给出实现这些直线回归分析所需要的SAS程序及输出结果。

简单线性回归分析；SAS程序；加权直线回归分析；重复试验的线性回归分析

*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

1 概 述

简单线性回归分析是研究两定量变量之间依存变化关系的一种最常用最简单的方法。如何正确实现简单线性回归分析，需要考察以下两组前提条件。

第一组前提条件，即从数理统计学角度考量所归纳出来的前提条件[1]：①自变量X可以是普通变量，也可以是随机变量，但因变量Y必须是随机变量；②线性，即因变量Y与自变量X之间的关系为线性关系，在直角坐标系内绘制关于X与Y的散点图，可以看出线性关系；③独立性，即各个观察对象之间必须是相互独立的；④正态性，即给定X的取值后，Y服从正态分布；⑤等方差性，即不同X值对应的Y的分布具有相同的方差。

第二组前提条件，即从基本常识角度考量所归纳出来的前提条件：①对于两个定量变量而言，所有受试对象应具有同质性；②所研究的两个定量变量在专业上应具有一定的联系；③在直角坐标系中绘制(X,Y)的全部散点，全部散点应呈现直线变化趋势；④散点图上不存在下列两类可疑的异常点，第一类，在垂直于横坐标轴方向上的可疑异常点，第二类，在假定的理想直线的左右两端的延长线方向上的可疑异常点。

事实上，上述的第二组前提条件更有实用价值，它也是进行简单直线回归分析的基本步骤。在此基础上，再计算直线回归方程中的参数并对参数进行假设检验；最后，再将所获得的简单直线回归方程用于“预测(给定自变量的数值去计算因变量的取值)”或“控制(给定因变量的取值去估算自变量的变化范围)”。

2 简单直线回归分析

简单直线回归模型为：

y=α+βx+ε

(1)

简单线性回归分析的任务：其一，估计式(1)中参数α和β的数值；其二，假设检验，包括对截距、斜率和整个直线回归方程的检验。

【例1】研究20名儿童的血红蛋白(y)与血铁(x)之间的关系[2]，数据见表1。

【分析与解答】对表1资料进行简单直线回归分析所需要的SAS程序如下：

data jz; input n y x@@; cards;

113．5518．7213467．3311469．8414．3456．6512．5448．7612．5424．1

711．8405．6811．5446911416．71010．7430．81110．2409．81210384．1139．5356．3149．4388．6158．8325．9166．3292．8177．3332．8187．8283197．3312．5207294．7

; run;

proc gplot data=jz; plot x*y='s'; run;

proc reg data=jz; model y=x/noint; run;

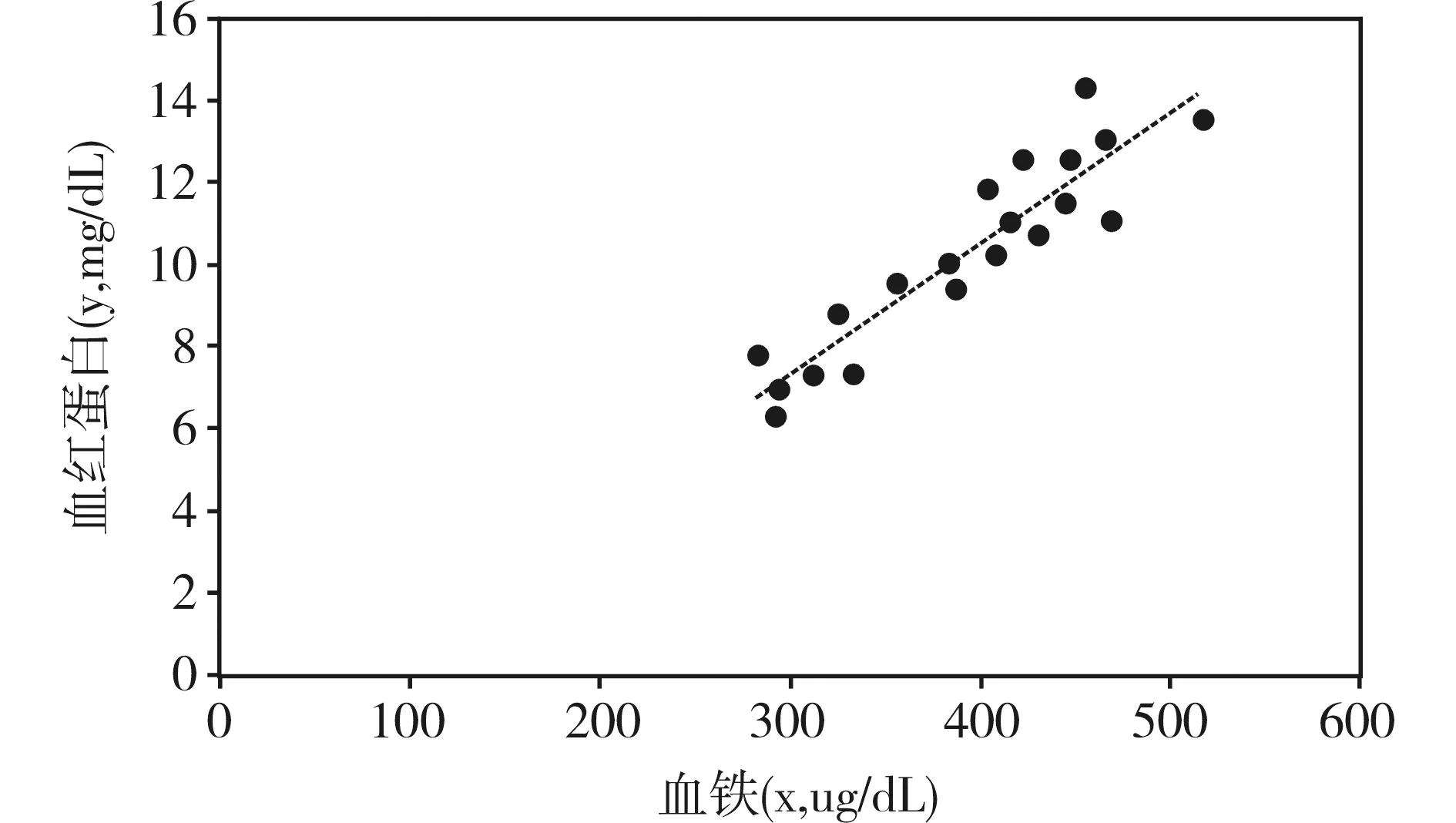
图1 20名儿童的血红蛋白(y,mg/dL)与血铁(x,ug/dL)的散点图

简单直线回归分析的假设检验结果见表2、表3。

表2 方差分析

表3 参数估计

所谓经验决策是决策者凭借经验制定决策的活动和过程，［7］经验决策主要的推理过程是逻辑学中的类比推理，其最为主要的推理过程是:

3 加权直线回归分析

医学或药学试验中经常需要计算引起试验动物总体中半数动物产生某种反应所需的药物(或毒物)剂量，即半数有效量，需要使用到加权直线回归分析[1]。

【例2】SAS 9.3帮助文档中Probit过程中第一个例子，研究不同剂量药物下小鼠反应数。数据见表4。

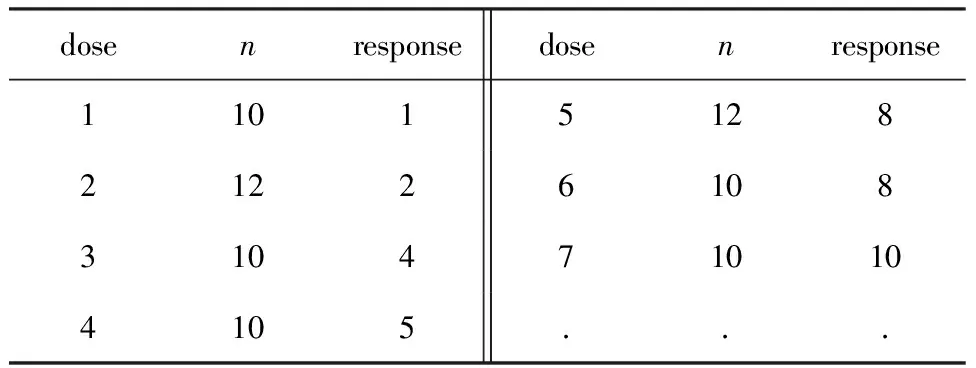
表4 不同剂量药物下小鼠反应数

注：dose代表剂量，n代表每个剂量组的动物数，response代表每个剂量组的阳性反应动物数

【分析与解答】对表4资料进行加权直线回归分析所需要的SAS程序如下：

data a; input Dose N Response @@; datalines;

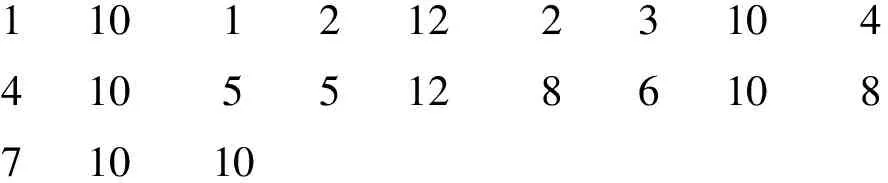
11012122310441055128610871010

;

run;

output out=B p=Prob std=std xbeta=xbeta; run;

参数估计结果见表5。

表5 参数估计

所求得该药物的半数反应剂量为3.39096。见表6。

表6 半数反应剂量

4 具有重复试验的直线回归分析

在同一试验条件下进行多次重复试验，研究因变量与自变量之间是否存在直线关系时可以用具有重复试验的直线回归分析。

具有重复试验的直线回归分析与无重复试验的直线回归分析的区别在于：前者可以对“失拟(即直线回归方程所不能解释的那部分信息)”进行假设检验，仅当“失拟”的检验结果无统计学意义时，可将其视为无重复试验的情形，但试验点数为不同X值个数乘以重复试验次数(各X值对应的重复试验次数相等)；否则，应选择合适的曲线类型，进行曲线回归分析。

【例3】研究不同血液浓度与血红蛋白含量之间的关系[1]。数据见表7。

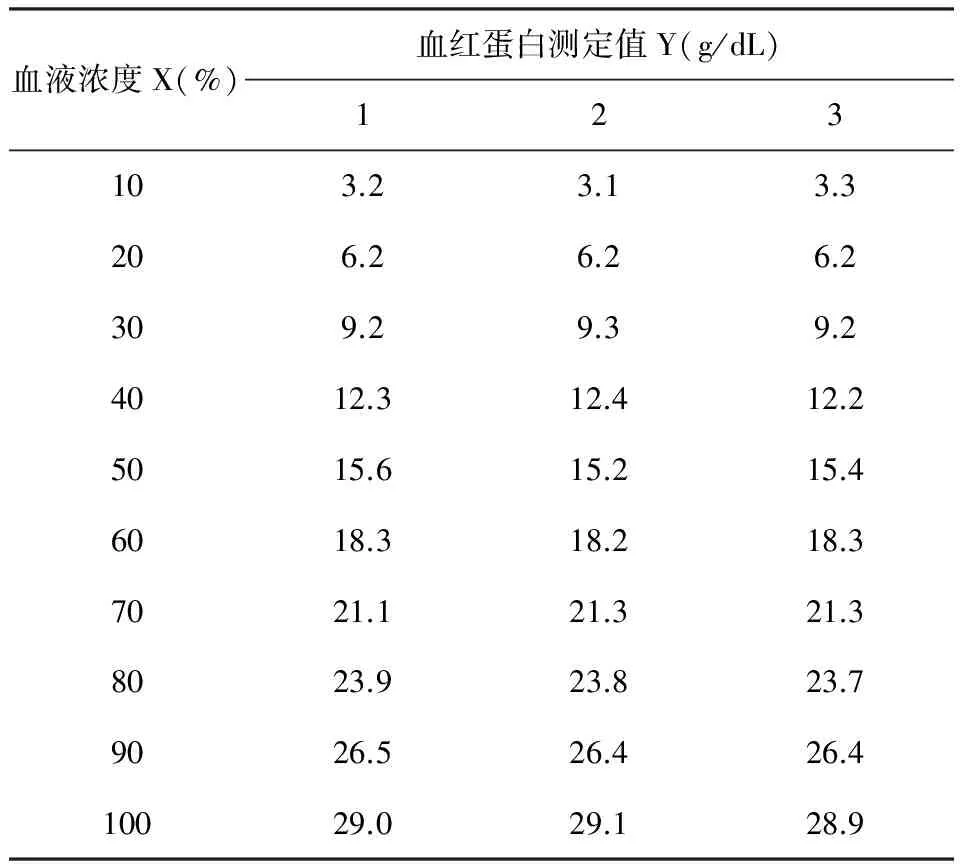
表7 不同血液浓度下血红蛋白的测定值

【分析与解答】 对表7资料进行具有重复试验的直线回归分析所需要的SAS程序如下：

data b; input x n@@; g=_n_; do i=1 to n; input y@@; output; end; cards;

1033．23．13．32036．26．26．23039．29．39．240312．312．412．250315．615．215．460318．318．218．370321．121．321．380323．923．823．790326．526．426．4100329．029．128．9

;

run;

proc glm data=b; class g;model y=x g/ss1; run;

proc reg data=b; model y=x; run;

具有重复试验的直线回归分析较简单直线回归分析多了失拟检验，目的是考察仅采用直线回归方程是否可以较好地拟合给定的资料。失拟检验的结果见表8。

表8 本例资料的失拟检验结果

在表8中，只需看最后一行，对分组变量g(它在本质上就是自变量不同取值的个数)进行检验即可，这里F=29.57，P<0.0001，说明失拟平方和基本上是由模型分组因素造成，也就是说，该资料未通过失拟检验，不能直接拟合简单直线回归方程，而需要根据散点图中全部散点的分布趋势和形态，选定合适的曲线类型并拟合之。

究竟如何进一步处理此资料，请读者阅读完本期中的下一篇文章《简单曲线回归分析及其应用》后，自己去把它完成。提示：若采用二次抛物线、对数函数曲线、指数函数曲线或幂函数曲线来分别拟合本例资料，从模型的假设检验的F值和复相关系数平方(即R2)的数值越大越好以及残差图中散点分布情况(全部散点在残差为0的水平线上下随机波动且无明显变化趋势为好)来全面考量，相对来说，本例资料拟合二次抛物线最好。

[1] 胡良平.科研设计与统计分析[M].北京: 军事医学科学出版社, 2012:381-400.

[2] 徐天和, 柳青.中国医学统计百科全书 多元统计分册[M].北京: 人民卫生出版社, 2004: 2.

Simplelinearregressionanalysisanditsapplication

GuHengming1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China

The aim of this article is to introduce the preconditions, categories, SAS programs and the results interpretation of the simple linear regression analysis to illustrate how to choose the correct regression model and whether the data is worth regression analysis. There are three kinds of simple linear regression analyses: simple linear regression analysis, weighted linear regression analysis and repeated experimental linear regression analysis. The following examples are used to illustrate different simple linear regression analyses and the corresponding SAS programs required to perform these linear regression analyses and their results.

Simple linear regression analysis; SAS Program; Weighted linear regression analysis; Repeated experimental linear regression analysis

国家高技术研究发展计划课题资助(2015AA020102)

R195.1

A

10.11886/j.issn.1007-3256.2017.06.002

2017-12-03)

陈 霞)