经典统计的回归模型概述
谷恒明,胡良平,2*
(1.军事医学科学院生物医学统计学咨询中心,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu812@sina.com)
科研方法专题
经典统计的回归模型概述
谷恒明1,胡良平1,2*
(1.军事医学科学院生物医学统计学咨询中心,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu812@sina.com)
本文目的是系统全面地总结和归纳经典统计中的回归模型及其合理选用的要领。具体方法是先按因变量的性质分为定量因变量与定性因变量两大类,再分别按自变量所具备的不同前提条件,并基于经典统计思想构建相应的回归模型。初步结果为:在定量因变量的场合下,经典回归模型大致有16种不同情形;而在定性因变量的场合下,经典回归模型大致有6种不同情形。总之,在构建经典回归模型时,应当依据因变量的性质和自变量所具备的前提条件,选择最合适的回归模型,才能达到比较理想的统计分析目的。
自变量;因变量;变量变换;多重共线性;多重线性回归模型
*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)
1 引 言
1.1 何为回归分析
统计学上,统计学家用一个函数关系式将因变量随自变量变化而变化的关系呈现出来,并称其为回归方程(对样本而言)或回归模型(对总体而言)。而在具体实践中,人们常把回归方程与回归模型视为同一个东西,在称呼时带有随意性。回归分析通常包括构建回归方程、对其回归系数进行假设检验和区间估计(即由样本去推论总体的规律,在本质上是希望得到或接近回归模型),最终目的是在给定自变量的新取值条件下,预测因变量的取值;少数场合下,会给定因变量的取值,把握自变量的取值区间(即用于控制)。
1.2 构建回归方程并求解的方法
一般来说,构建回归方程并求解的方法有以下三种。
其一,经典回归分析法。仅依据样本信息并结合专业知识人为构建一个回归方程A,再依据某些假定(如因变量服从某种特定的概率分布)和数学技术或原理(如最小二乘法或其改进方法、最大似然法或其改进方法、广义估计方程法等)派生出一个方程组B,方程组B中包含的方程个数为方程A中待定回归系数的个数再加1(用于估计回归方程中的一个待定的常数项)。采用各种数值计算技术或迭代计算技术求出方程组B的解,也就获得了方程A中全部待定系数的估计值(包括截距项和全部自变量前的回归系数)。根据对因变量所做出的假定不同,还可细分为“参数回归分析法”“半参数回归分析法”和“非参数回归分析法”。
其二,贝叶斯回归分析法。在经典回归分析的基础上,再利用总体的有关信息,附加上关于回归方程中待估参数的“先验信息”,并借助马尔科夫链蒙特卡罗算法(简称MCMC算法[1]),获得回归系数的“后验信息”,进而获得回归方程中各待定系数的平均估计值(即基于m次随机抽样数据算得m个回归方程中的待定系数,求取同一个待定系数的算术平均值作为该待定系数的最终估计值)。
其三,机器学习回归分析法[2]。此法与前述两种方法有较大区别且有多种解决问题的思路,即现代回归分析中所提及的“神经网络回归分析法”“决策树回归分析法”“随机森林回归分析法”和“支持向量机回归分析法”等。因篇幅所限,此处暂不赘述。
1.3 本文将涉及的范围
因篇幅所限,本文仅粗略介绍与“经典回归分析”有关的主要内容。其基本思路是:先按因变量分为定量和定性两种场合,再按自变量所具备的前提条件,分别进行概述和总结。
2 因变量是定量变量的回归分析
2.1 自变量只有一个且不需要对变量进行变换——简单线性回归分析
简单线性回归分析是定量地研究两个变量之间线性关系的方法,模型为:
y=α+βx+ε
(1-1)
其中:y是因变量,x是自变量,ε是误差项。
2.2 自变量只有一个,需要适当变换的回归分析
当因变量随着自变量变化关系不呈直线,而是曲线时,就需要对因变量和/或自变量进行相应的变换。一般变换有以下几种:
(1)当因变量y随着x的变化符合指数曲线规律时,可以对因变量y取对数变换,使指数曲线直线化。指数函数的一般形式为[3]:
y=aebx+k或y=aexp(bx)+k
(1-2)
其中:a≠0,k为渐近线。当不考虑k时,对式(1-2)等号两端同时取对数,得:
y1=lna+bx
如果以y1和x在直角坐标系内绘制的散点图呈直线变化趋势时,就可以考虑采用指数曲线来拟合和解释y与x之间的关系。
(2)当因变量y随着x的变化符合幂函数曲线规律时,可以对自变量x和因变量y同时取对数变换,使幂函数曲线直线化。幂函数的一般形式为:
y=axb+k(a>0,x>0)
(1-3)
当不考虑k时,对式(1-3)等号两端同时取对数,得:
y1=lna+blnx
此时以y1和lnx在直角坐标系内绘制的散点图呈直线变化趋势时,就可以考虑采用幂函数曲线来拟合和解释y与x之间的关系。
(3)当实测数据曲线呈拉长的“S”形或“乙”字形,其形状只升不降(正“S”形)或者只降不升(反“S形”)。此时可以考虑拟合Logistic曲线回归方程。多用于发育、繁殖、动态率、剂量反应及人口等方面的研究。一般形式为:
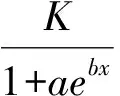
(1-4)
(4)当以百分数P为因变量时,若其随自变量变化的规律呈“S”形曲线时,取P的Logit变换值为y。
Logit变换公式为:
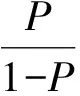
(1-5)
(5)当因变量的一系列取值可与标准正态分布曲线下的一系列累计面积(%)一一对应时,可建立其与标准正态分布曲线下横坐标值x之间的关系,此时,可称为对y进行Probit变换。
Probit公式为:

(1-6)
其中:μ为均数,是正态曲线面积下相当于50%时横坐标轴上的值,(x-μ)/σ为标准正态离差,加5是为了消除可能存在的负数以便于计算。
(6)当因变量与自变量不是简单的一阶关系,而是与自变量的二阶甚至高阶存在线性关系时,就需要使用多项式回归分析方法。P阶多项式回归模型为:
y=β0+β1x+β2x2+…+βpxp+ε
(1-7)
其中:βk(k=1,…,p)称多项式回归系数。p=2时,称二项式回归,依次类推。当p值太大时(p≥6),自变量x各阶之间容易发生共线性问题,因此p常取不大于5的值。若散点图呈抛物线,可以考虑二项式回归方程,通常叫做抛物线回归方程;当散点图呈波峰波谷成对出现时,可以考虑三项式回归方程。
(7)结果变量为计数的,初期增长缓慢,随后增长速度逐渐加快,达到一定程度后又逐渐减慢,最后达到饱和状态,呈这种变化趋势时,可以选用Compertz曲线回归方程。
以上7个公式的散点图皆是可以通过变量转换,达到曲线直线化的目的,因此在拟合一个因变量与一个自变量的回归方程时需要先作散点图并观察其特点,以便选用相适应的变量转换,使曲线变换为直线,得到直线回归方程,最后再还原到初始变量。
进行曲线拟合时需要注意:由于生物医学的特点,资料的散点图往往不是完整的抛物线或波浪线,有可能仅是其中一段,需注意结合散点图的变化趋势选择合适的曲线类型,没有把握时,多选用几种最接近的曲线类型,以因变量的计算值与观测值之间的偏差平方和最小为判定标准,确定最合适的曲线类型。
2.3 含有多个自变量且不存在共线性的多重线性回归分析
研究一个计量因变量和多个自变量之间的线性关系,一般选用多重线性回归分析,多重线性回归分析一般模型为:
y=β0+β1x1+β2x2+…+βmxm+ε(m=1,2,…)
(1-8)
其中:β0为截距项,βk(k=1,…,m)为各个自变量的偏回归系数,ε为误差项。通常基于最小二乘原理推导出正规方程组,求解此方程组便可获得截距项和全部回归系数的估计值。
2.4 含有多个自变量且存在共线性的回归分析
以下为两种消除或减弱共线性影响的改进回归分析方法:
(1)主成分回归分析基本原理与计算方法:
①以因变量Y和全部自变量X1,X2,…,XP进行多重线性回归,并诊断全部自变量之间的多重共线性[4]。
②将原来的具有共线性的回归变量(即自变量)X1,X2,…,XP进行主成分分析,得出相关系数矩阵的特征值、贡献率和累积贡献率。
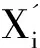
(1-9)
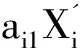
(1-10)

④做回归自变量选择。用累计贡献率≥80%所包含的m个主成分变量代替原来的P个自变量,建立主成分回归方程。
⑤将主成分Zm的表达式回代到回归方程中,再将标准化变量还原为最原始的自变量,便可以得出因变量对原始自变量的回归方程。
(2)岭回归分析基本原理与计算方法:
①多重线性回归的回归系数可以表示为:
β=(X'X)-1X'Y
(1-11)
其中X为自变量的n×m阶矩阵,X'为X的转置矩阵,(X'X)为对称的m×m方阵,(X'X)-1为(X'X)的逆矩阵,Y为因变量n×1向量。β为回归系数的m×1向量。
②岭回归分析方法对回归系数估计的方法如下:
β(k)=(X'X+kIm)-1X'Y
(1-12)
即在矩阵(X'X)的主对角线元素上加上一个非负因子k,其中Im为m阶单位矩阵,k>0,称为岭参数。
③模型系数随参数k变化的曲线称为岭迹图,可以根据岭迹图变化的形状来确定k值和进行自变量的筛选。确定k值的方法还有方差膨胀因子法和残差平方和法。
④选择变量的标准
A.在岭回归计算中,剔除标准化岭回归系数比较稳定且绝对值很小的自变量。
B.当k值较小时,标准化岭回归系数并不小,但随k值增加而迅速趋于0的自变量应剔除。
C.剔除使回归系数很不稳定的自变量。
2.5 基于Possion分布的Possion回归分析
Possion回归方程用于描述单位时间、面积或空间内某事件发生数的影响因素分析方法。Possion回归模型一般形式为:

(1-13)
其中:d表示单位时间或空间事件发生数,X表示观察事件发生数。
2.6 数据存在过离散时的负二项回归分析
负二项回归和Possion回归类似,都适用于因变量为计数的资料。但Possion要求均数和方差相等,实际数据中往往不符合,学者们引入了负二项回归。在医学研究中,很多事件的发生是非独立的,此时可以采用负二项回归进行分析。负二项回归模型为:
g(μi)=g(E(yi))=β0+β1xi1+β2xi2+…+βmxim,i=1,2,…,n
(1-14)
2.7 生存资料的回归分析
2.7.1 生存资料Cox模型回归分析
它可以同时分析众多因素对生存时间的影响,不受生存分布类型的影响。回归模型形式为:
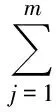
(1-15)
其中:hi(t)为第i名受试者生存到ti时刻的危险率函数,h0(t)是当所有危险因素不存在时的基础危险率函数。
2.7.2 生存资料参数模型回归分析
生存资料参数模型回归分析,即生存时间分布符合某一分布,通常有指数分布、Weibull分布、对数正态分布、Gamma分布等。此时需要根据数据的具体分布类型选择与其相适应的参数模型进行回归分析。
2.8 分位数回归分析
主要描述因变量Y的分位数与自变量X之间的线性依赖关系。当数据中存在较多的异常值,通常基于正态分布假定的多重线性回归方程拟合效果不好,而采用因变量Y的百分位数拟合效果好,此时可以考虑分位数回归分析。分位数回归较通常意义下的多重线性回归的优点:①如果要估计的模型存在异方差,不会影响估计的结果;②能够在不同的分位数水平下全面刻画分布的特征,特别适合极端值和尾部分布的研究;③估计结果不受离群值(极端值)影响,具有很强的稳健性[5]。分位数回归模型为:
yi=β0+β1x1+β2x2+…+βnxn+ε(n=1,2,…)
(1-16)
其中:yi为因变量的分位数,其余与通常的多重线性回归模型相同。
2.9 因变量的取值为随自变量变化而呈现出“累计发生率”的Probit回归分析
Probit回归方程可用于描述因变量的一系列取值为随自变量变化而呈现出“累计发生率”的多重回归分析问题,例如某种药物阳性反应率。如果用P=P(Y=1|X)表示在自变量取值为X时阳性结果发生率,那么Probit回归模型可以写成:
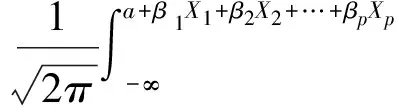
(1-17)
或Φ-1(P)=a+β1X1+β2X2+…+βpXp
(1-18)
其中:α和β1,β2,…,βp分别是模型的常数项和回归系数。
值得一提的是,前面第2.2节中的(5)“Probit变换”与此处的“Probit回归分析”在本质上是一回事。
3 因变量是定性变量的回归分析
3.1 因变量为二值变量的Logistic回归分析
当观测对象为一个个的受试对象时,二值Logistic回归分析与Probit回归分析类似,皆属于二值资料的概率回归分析问题。然而,Probit回归分析中的因变量的一系列取值皆为0~1之间的概率值且呈现出“累计概率”的形式,事实上,此时的观测对象不是一个个单独的个体,而是一组组的“群体”,即全部群组按自变量取值由小到大排序后,对应的各群组中某现象的发生率呈现递增的变化趋势,其最小值可以为0.00%、最大值可以为100.00%;Logistic回归分析中的因变量取值皆为0或者1,即观测对象皆为一个个的单独的个体。P=P(Y=1|X)表示在自变量取值为X时阳性结果发生的概率,Logistic回归模型的基本形式如下。
阳性结果不出现的概率表达式为:
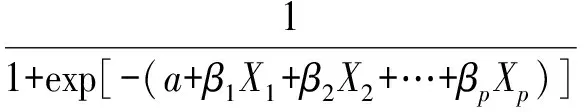
(2-3)
阳性结果出现的概率表达式为:
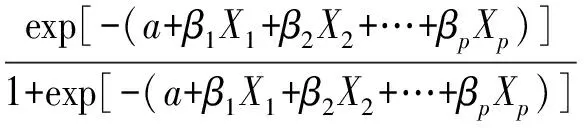
(2-4)
式(2-4)与式(2-3)中两个概率比数的自然对数为:
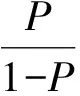
(2-5)
3.2 因变量为多值无序变量的多项分类Logistic回归分析
多项分类Logistic回归模型是二值Logistic回归模型的拓展,适用于一些因变量结果多于两个的资料。例如研究不同疾病、不同性别的患者与所用药物种类频数构成的关系。多项分类Logistic回归模型为:
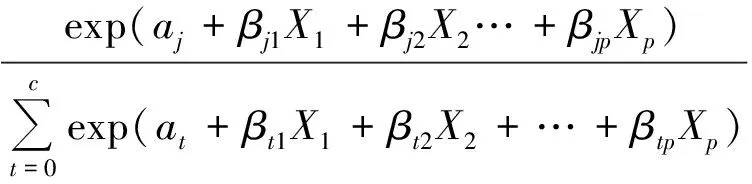
j=0,1,2,…,c
(2-6)
其中:a0=0和β0k=0(k=1,2,…,p),aj和βj1,βj2,…,βjp为未知参数。0~c表示c+1个不同无序结局,Pj表示结局为j时的概率。
3.3 因变量为多值有序变量的有序Logistic回归分析
当因变量为多值有序变量时,例如疾病严重程度、治疗效果等,皆可以使用有序Logistic回归模型进行分析。有序Logistic模型很多,应用最广泛的是累积Logistic模型,而且可以通过统计软件实现。
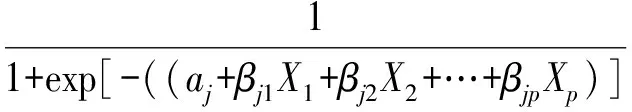
j=0,1,2,…,c
(2-7)
其中:aj和βj1,βj2,…,βjp为未知参数。0~c表示c+1个不同有序结局,Pj表示结局为j时的概率。
3.4 观测结局不独立的二水平Logistic回归分析[6]
因变量为二值变量,但各个观测结果并不互相独立,此时使用一般Logistic回归模型分析就不合适。可采用多水平Logistic回归模型分析,一般模型为:
(2-8)
其中:X是固定效应的解释变量设计矩阵,Z是随机效应的解释变量设计矩阵,β是水平1固定回归系数向量,U是随机回归系数向量,服从均值为0、协方差为矩阵G的正态分布。
3.5 观测结局不独立的二水平多值无序变量的Logistic回归分析[6]
因变量为多值无序且各个实验组的观测结局不是完全独立,此时可以使用二水平多项分类Logistic回归模型,其模型为:
(2-9)
其中:βj是与设计矩阵X相对应的固定效应向量,Uj是与设计矩阵Z相对应的随机效应向量。随机效应服从均值为0的正态分布。
3.6 观测结局不独立的二水平多值有序变量的Logistic回归分析[6]
因变量为多值有序变量且各个实验组的观测结局不是完全独立,此时可以使用二水平多层累积Logistic回归模型,其模型为:

(2-10)
其中:X是固定效应的解释变量设计矩阵,Z是随机效应的解释变量设计矩阵,β是固定效应,U是服从均值为0的正态分布的随机效应。
[1] 黄长全. 贝叶斯统计及其R实现[M].北京: 清华大学出版社, 2017:114-138.
[2] 吴喜之.复杂数据统计方法——基于R的应用[M]. 3版. 北京: 中国人民大学出版社, 2015:18-146.
[3] 徐天和, 柳青.中国医学统计百科全书 多元统计分册[M].北京: 人民卫生出版社, 2004:142-144.
[4] 徐林.利用SPSS进行主成分回归分析[J].宁波技术学院学报, 2006, 10(2):67-69, 74.
[5] Bittencourt M. Financial development and inequality: Brazil 1985-1994[J]. Economic Change and Restructuring,2010, 43(2): 113-130.
[6] 胡良平.面向问题的统计学——(2)多因素设计与线性模型分析[M].北京: 人民卫生出版社, 2012:482-490.
Summarizationofregressionmodelofclassicalstatistics
GuHengming1,HuLiangping1,2*
(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China
The aim of this paper is to systematically summarize the regression models in classical statistics and the essentials of their rational selection. The concrete method of construct in the corresponding regression model based on the classical statistical thought is as follows: the first step is to divide the dependent variables into two categories-the quantitative dependent variable and the qualitative dependent variable according to the nature of the dependent variables; the second step is that the independent variables have the preconditions to be taken into account. The preliminary result is as follows: in the case of quantitative dependent variable and qualitative dependent variable there are roughly 16 and 6 different situations in the classical regression models. In short, when building a classical regression model, the most suitable regression model must be selected according to the nature of the dependent variable and the preconditions of the independent variables to achieve the aim of the ideal statistical analysis.
Independent variable;Dependent variable; Variable transformation; Multicollinearity; Multiple linear regression model
国家高技术研究发展计划课题资助(2015AA020102)
R195.1
A
10.11886/j.issn.1007-3256.2017.06.001
2017-12-03)
陈 霞)
——与非适应性回归分析的比较

