铅酸电池剩余放电时间预测模型与求解
彭亚发
(浙江安防职业技术学院 信息工程系,浙江 温州 325016)
0 引 言
铅酸电池被广泛应用于工业、军事、日常生活中。铅酸电池经过长时间使用或放置,充满电后的荷电状态会发生衰减,要准确预测电池在当前负荷下以当前电流强度放电到最低保护电压的剩余放电时间非常困难。针对铅酸电池的剩余放电时间预测,学者开展了诸多研究。如李勃等采用Levenberg-Marquardt优化的BP神经网络,进行模糊分类及自适应求解,并预测电池在断电状态下的供电时间[1]。王宏亮等就铅酸电池剩余放电时间建立了改进的卡尔曼滤波算法,并结合该算法提出基于双卡尔曼滤波的铅酸电池SOC估算方法[2]。总体上看,这些方法都
有一定的局限性。为了准确预测铅酸电池剩余放电时间,在不考虑铅酸电池的自放电,即铅酸电池在不工作时存在放电现象,以及铅酸电池工作环境不变,即不考虑环境对铅酸电池影响的情况下,绘制以固定电流放电时的放电曲线,针对放电的不同阶段,分析其中的放电规律,选取不同初等函数对放电曲线进行拟合,最后计算出不同初等函数拟合放电曲线的平均相对误差(MRE),择优得到电压随放电时间的最佳拟合曲线。
1 铅酸电池放电曲线规律分析
为了分析铅酸电池放电曲线规律,在选用初等函数对铅酸电池放电曲线进行描述时,先根据电压随时间变化值,分别绘制放电曲线,分析放电曲线规律。通过对铅酸电池固定电流为20A时的放电情况进行实证分析,将放电曲线划分为放电初期、中期和末期三个阶段,最后借助MRE值的计算方法,对铅酸电池放电曲线进行分阶段和整体拟合,并对拟合结果加以分析,以期准确分析铅酸电池放电规律。
1.1 MRE值的计算方法
设n, n, n分别代表三个阶段所测电压样本点总123数,先按比例分配,即放电初期应选取样本点个数电中期选取样本点个数为:p=2电末期选取样本点个数若某一阶段存在p< n(i=1, 2, 3),则p=n。剩下213-ninipn个应选采样点,按照相同方法进行分配。
MRE计算公式为:

其中,Z为根据模型得到的预测剩余放电时间,Z'为对应实际测量的剩余放电时间,n为样本点个数。
通过以上方法对20~100A的固定电流放电曲线进行分阶段和整体拟合,计算出MRE值(见表1)。
由表1可知,对铅酸电池放电曲线进行分段处理得到的MRE值要小于整体处理的MRE值,即分段处理模型的精度比整体拟合更高。
1.2 放电规律分析
铅酸电池放电规律主要对其固定电流20A时放电曲线的拟合进行实证分析。通过MATLAB工具箱计算得到铅酸电池放电初期不同拟合函数的MRE值(见表2)。
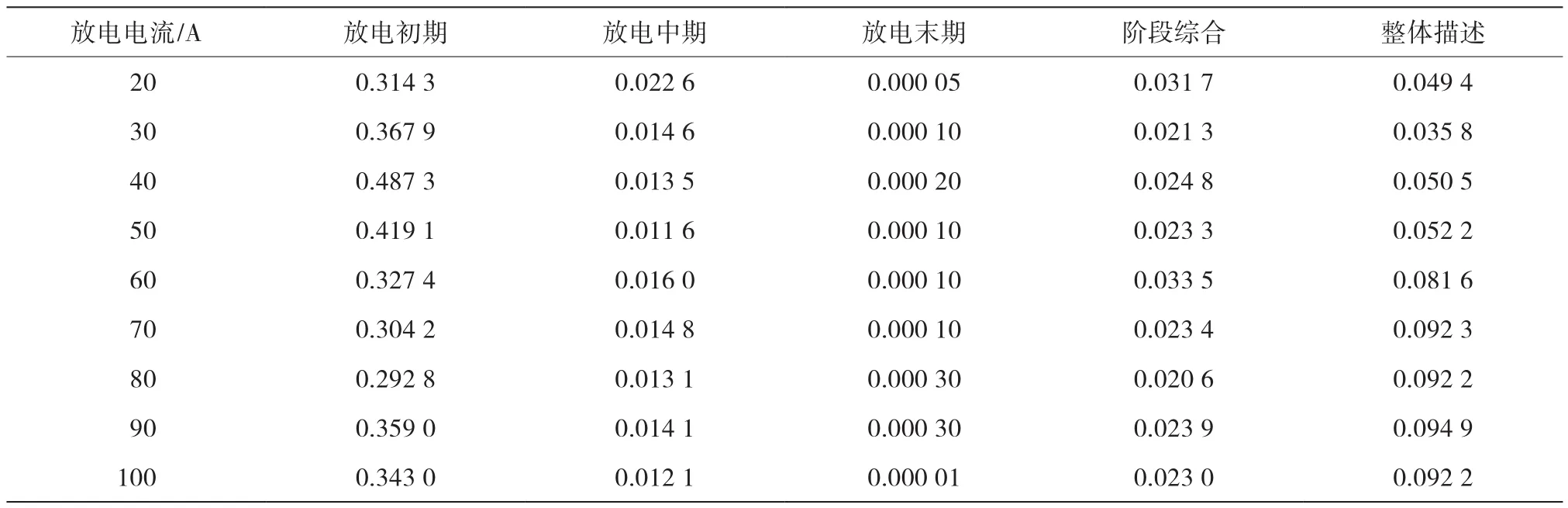
表1 铅酸电池放电曲线拟合MRE值

表2 铅酸电池放电初期不同拟合函数的MRE值
由表2可知,采用四种函数对铅酸电池固定电流20A时放电初期曲线进行拟合时,拟合效果最好的函数为:
f (x) = a0+ a1cos(ωx)+ b1sin(ωx)
铅酸电池以固定20A电流放电初期曲线拟合为:
f (x)=5.76+46.29cos(-8.947x)-79.88sin(-8.947x)
其中,x为放电时间,f (x)为当前时刻铅酸电池的端电压。铅酸电池固定电流20A时放电初期拟合曲线与实际曲线的比较如图1所示。
由图1可看出,初期拟合效果并不好,主要原因可能在放电初期铅酸电池电压不稳定,由于铅酸电池自身原因造成放电电压骤减之后又出现回升。

图1 铅酸电池固定电流20A时放电初期拟合曲线与实际曲线的比较
铅酸电池固定电流20A时放电中期曲线拟合为:
f (x) = -63.43x3+494.5x2+6337x-4.707×104
其对应的MRE值为0.022 6。铅酸电池固定电流20A时放电中期拟合曲线与实际曲线的比较如图2所示。

图2 铅酸电池固定电流20A时放电中期拟合曲线与实际曲线的比较
由图2可看出,对比图1,图2的拟合效果显著提高,铅酸电池在放电中期拟合曲线与实际曲线吻合度较高,主要原因可能是,经过放电初期的调整,铅酸电池在放电中期电压不再表现出骤增骤减的现象。
铅酸电池固定电流20A时放电末期曲线拟合为:
f (x) = 1415x2-2.581×104+1.214×105
其对应的MRE值为0.000 05。铅酸电池固定电流20A时放电末期拟合曲线与实际曲线的比较如图3所示。
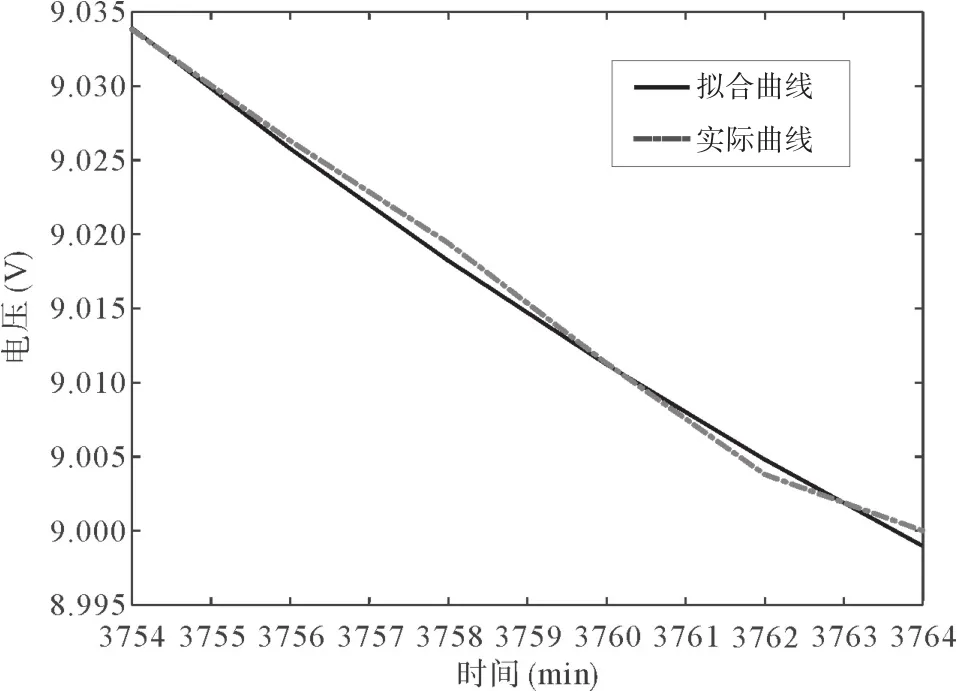
图3 铅酸电池固定电流20A时放电末期拟合曲线与实际曲线的比较
由图3可看出,对比图1和图2,图3的拟合效果最好,主要原因是经过放电中期放电,铅酸电池电压下降,在放电末期急速下降,该时段数据结构简单,因而具有较好的拟合效果。
2 预测模型比较分析
为了对比铅酸电池剩余放电时间预测模型的效果,主要对铅酸电池放电进行初等函数的整体描述精度,比较预测模型的拟合效果。通过f (x) = -1343+2.402×104-1.036×105函数进行拟合,对应的MRE值为0.049 4。铅酸电池固定电流20A时放电整体拟合曲线与实际曲线的比较如图4所示。

图4 铅酸电池固定电流20A时放电整体拟合曲线与实际曲线的比较
由图4可看出,以固定电流20A时放电整体拟合效果并不理想,尤其是放电初期和放电末期的拟合相差较大。
2.1 基于初等函数拟合的放电时间预测模型
根据得到的放电曲线模型,可对铅酸电池剩余放电时间进行预测。电压为9.8V时剩余放电时间的预测值见表3。
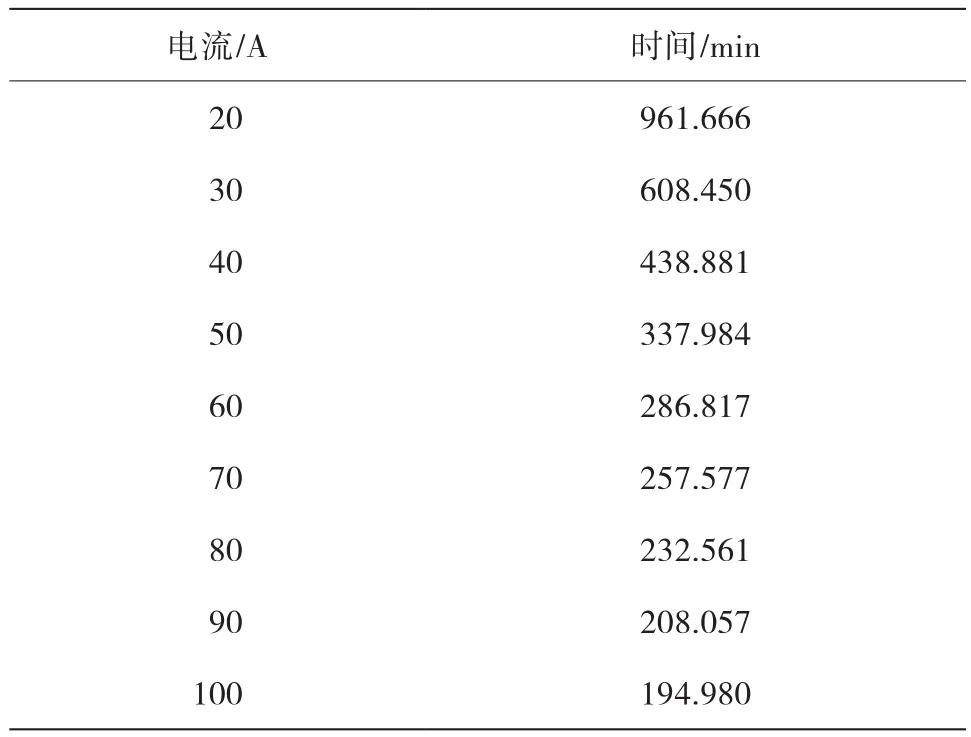
表3 电压为9.8V时剩余放电时间的预测值
首先对铅酸电池放电曲线规律进行分析,然后针对不同阶段进行分段拟合,在拟合中选取不同的初等函数,利用MRE得到最佳拟合函数,根据得到的最佳拟合函数对不同放电电流进行放电剩余时间预测[3]。
2.2 基于组合预测的任意电流放电曲线预测模型
(1)铅酸电池端电压与放电电路曲线分析。求解任意电流的放电电压曲线,分析相同时间不同铅酸电池以不同电流进行放电时电压随电流变化的曲线,如图5所示。
由图5可看出,在放电初期,电压随放电电流的增加而增加,之后随着放电电流的增大,放电电压逐步减小,在放电中期和放电末期,铅酸电池端电压随放电电流的增大而减小[4]。电压随电流的变化比较单一,没有放电曲线中出现的骤增和骤减,初等函数基本可满足图5各曲线的描述。

图5 铅酸电池端电压随电流变化的曲线
(2)基于多项式拟合的任意电流的放电电压预测模型。由于在同一时刻,只有20~100A 9个数据点,因而采用最简单的二次多项式对其进行拟合。铅酸电池放电起始时(0 min)各电流对应的电压见表4。
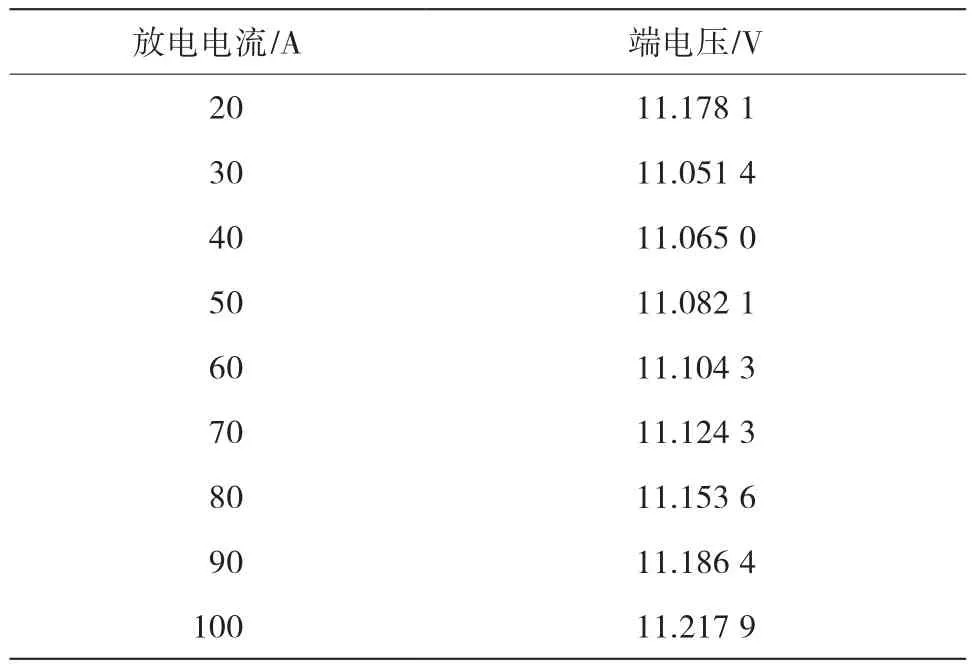
表4 铅酸电池放电起始时各电流对应端电压
利用MATLAB工具箱拟合得到,表4的关系式为:
V = 0.0058I2-0.0454I +11.17
其中,I为电流,V为电压。由此可计算0时刻铅酸电池固定电流55A时放电对应端电压为:11.085 V。同理,可计算其他时刻。铅酸电池固定电流55A时放电对应端电压见表5。

表5 铅酸电池固定电流55A时放电对应端电压
铅酸电池固定电流55A时放电曲线如图6所示。
由图6可看出,利用多项式拟合求解得到铅酸电池固定电流55A时放电曲线很不平滑,主要因为电流采样点只有20~10A,导致二次多项式精度不高。在实际测量中,电压应是光滑的曲线。
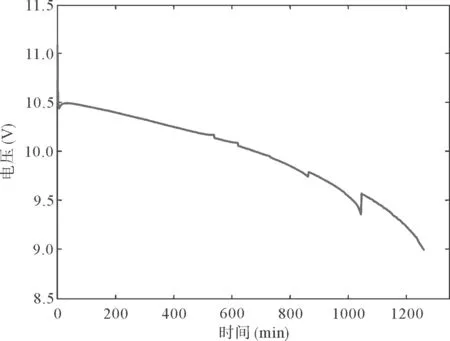
图6 铅酸电池固定电流55A时放电曲线
在得到铅酸电池固定电流55A时放电电流的电压时间序列后,就可对放电曲线进行分段拟合,从而最终得到拟合方程为:
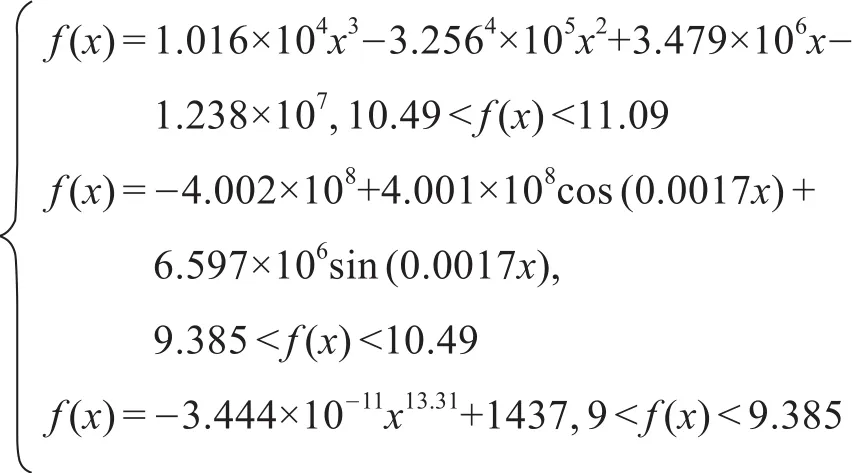
铅酸电池固定电流55A时放电曲线拟合MER值见表6。

表6 铅酸电池固定电流55A时放电曲线拟合MER值
至此,通过拟合方程可得到该时刻任意电流所对应的电压值,由此可得到铅酸电池以任意电流的放电曲线。
3 模型的建立与求解
3.1 模型的建立
考虑因变量Y与自变量X的建模问题。偏最小二乘回归的基本方法是:首先在自变量中提出第一成分t1,t1是x1, x2, …, xm的线性组合,且尽可能多地提取原自变量集的变异信息。同时在因变量中也提取第一成分u1,并要求t1与u1相关程度达到最大。然后建立因变量y与t1的回归,如果回归方程已达到满意的精度,则算法中止;否则继续第二对成分的提取,直到达到满意的精度为止。若最终对自变量集提取r个成分t1, t2, …, tr,偏最小二乘回归将通过建立y与t1,t2, …, tr的回归式,然后再表示为y与原自变量的回归方程式,即偏最小二乘回归方程式[5]。
为了方便起见,因变量组和自变量组的标准化观测数据阵分别记为F0, E0,即:
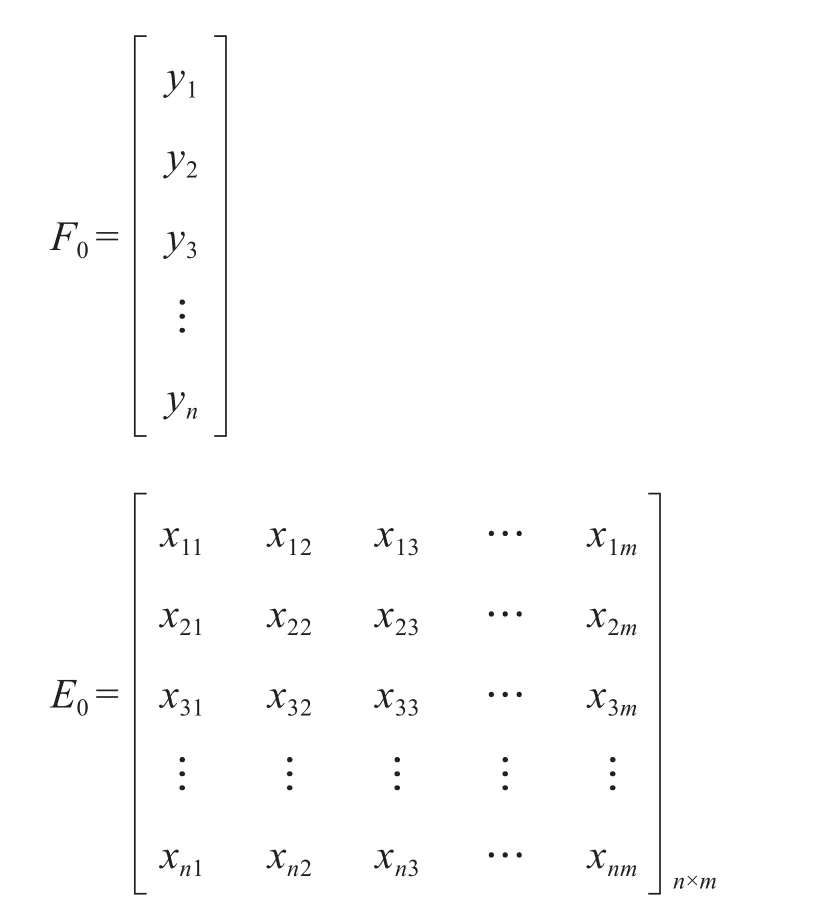
偏最小二乘回归模型建立的具体步骤如下:
(1)分别提取两变量组的第一对成分,并使之相关性达到最大。假设从两组变量分别提出第一对成分为t1, u1,t1是自变量集x1, x2, …, xm的线性组合:t1=合:u1=Y。为了回归分析的需要,由两组变量集的标准化观测数据阵E0, F0,可计算第一对成分的得分

(2)建立y对t1的回归及x1, x2, …, x5对t1的回归。假定回归模型为:

其中,α1=(α11, α12, α13, …, α1m)T, β1=(β11, β12, β13,…, β19)T分别是多对一的回归模型中的参数向量,E1,F1是残差阵。回归系数向量α1, β1的最小二乘估计为:
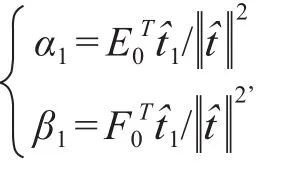
其中,α1, β1为模型效应负荷量。
(3)用残差阵E1, F1代替E0, F0,重复以上步骤。标准化观测数据阵E的秩为r≤min(n-1, m),则存在 r个成分t1, t2, …, tr,使得
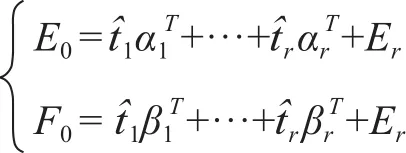
把tk=wkx1+…+wkmxm(k=1, 2, …, r)代入Y=t1β1+…+trβr,即得到因变量的偏最小二乘回归方程式。
3.2 模型的求解
不同主成分下保留因变量的信息变化如图7所示。
由图7可看出,当主成分选取4个时,主成分保留了99.99%的因变量信息。

图7 偏最小二乘回归主成分的选取
由此,最终得到铅酸电池在衰减状态3的放电时间表达式为:
t3=881.9385-84.4118V+0.3652T+0.4272t1-0.2372t2
其中,V为铅酸电池端电压,T为新电池放电时间,t1, t2分别为铅酸电池在衰减状态1和衰减状态2的放电时间。
通过拟合方程可得到铅酸电池在衰减状态3的放电曲线,如图8所示。

图8 铅酸电池在衰减状态3的放电曲线
通过回归方程可得到当电压为9V时的时刻为第829min,即从当前时刻第596min后经过233min铅酸电池放电完毕,电压下降到9V,因而铅酸电池在衰减状态3还可使用233min。
至此,建立以衰减状态3的放电时间为因变量,以铅酸电池电压、衰减状态1、衰减状态2的放电时间为自变量的偏最小二乘多元线性回归模型,求解得到铅酸电池在衰减状态3的剩余放电时间。
3.3 模型的优势
一是依据放电规律将铅酸电池固定电流时放电过程划分为初期、中期和末期三个阶段。对放电曲线分阶段建立基于初等函数拟合的预测模型,并采用MRE检验多种初等函数的拟合精度,同时也直接对放电曲线进行拟合。在得到放电曲线拟合方程后,便可计算剩余放电时间,模型根据铅酸电池放电规律对放电曲线进行分段处理,提高了预测精度。二是对在相同时刻铅酸电池电压与电流的关系进行分析,并对这一关系进行多项式拟合,即可得到该时刻任意电流所对应的电压。在获取一系列电压值后,利用所建立的模型,对放电曲线进行初等函数拟合。在求解任意电流的电压时,直接采用多项式进行拟合,操作方便简单。综合考虑铅酸电池衰减对剩余放电时间的影响,铅酸电池在三种衰减状态下的放电时间与铅酸电池的电压均有关系,因而通过模型比较建立的偏最小二乘多元线性回归模型更加直观。
4 结束语
本文建立的偏最小二乘多元线性回归模型在拟合和预测精度上都较传统方法有明显的优势。利用分阶段建立基于初等函数拟合的预测,并采用MRE检验多种初等函数的拟合精度的方法,让预测模型更加直观,且易于实现计算机编程。该模型的算法还能用于各类衰减现象的预测,后续将借助该模型应用于其他衰减的预测中,从而实现模型的推广价值。
[1] 李勃,刘云峰,郑益.蓄电池剩余放电时间综合分析模型研究[J].煤炭技术,2011,30(12):51-53.
[2] 王宏亮,崔胜民.基于试验的铅酸电池充放电特性模型的建立[J].蓄电池,2005,42(1):38-40.
[3] 彭金春,陈全世,韩曾晋.电动汽车的铅酸电池充放电过程建模[J].汽车技术,1997,40(6):5-6.
[4] 吴红斌,顾缃,赵波,等.典型蓄电池的建模与荷电状态估算的对比研究[J].电子测量与仪器学报,2014,28(7):88-90.[5] 毛丽霞.铅酸电池剩余放电时间的研究[J].当代化工,2017,46(8):1556-1559.

