基于Matlab的铁附件虚拟包装优化设计

钱哨，申进，胡举纲，李亮，仇爱军，卞振华，季明星

（1.国网江苏省电力有限公司盐城分公司，盐城 224051；2.盐城工学院，盐城 224051）

引言

铁附件是电力线路输变电用构（附）件的俗称，是根据用户的特殊要求而进行生产的非标准件产品，范围覆盖10kV及35kV、110kV、220kV输电线路及变电站用构件，以及交通和市政用到的一些非标件。由于其形状不规整，占地面积较大，所以对铁附件仓储带来很大的困扰。

主要存在问题如下：（1）同种型号不同厂方尺寸规格的不一致；（2）结构不规整导致摆放仓储凌乱；（3）进出库计数和发放困难；（4）占地面积大不符合仓储5S标准。如何有效的解决各类铁附件产品的仓储就涉及到其规格尺寸标准化、包装标准化和仓储标准化的问题。

本文根据目前铁附件包装存在的问题，结合包装容器结构设计的主要特点，利用Matlab编程软件对典型铁附件零件进行了包装结构优化设计，并且结合NX软件实现铁附件包装的虚拟装配和分析。

1 铁附件零件特点分析

常见的铁附件零件种类包括了扁铁成套抱箍、扁铁洋元抱箍、电缆抱箍、连接铁、横担、顶套等多种规格多种型号。其尺寸系列和形状结构各不相同。仅扁铁洋元抱箍又分为直径100到直径400等40种不同尺寸规格。目前铁附件零件仓储面临的最大问题就是安放的杂乱无章，没有一种统一的包装设计。并且对于零件的清点计数、发放等都带来了很大的问题。设计一种内部结构可调整，外部结构尺寸统一的包装箱是目前铁附件零件仓储急需解决的问题。

2 结构优化设计分析

根据铁附件零件的结构特性，并且结合设计需求，最终的包装箱必须能够安放在货架之上，并且每个包装箱承载的重量受到货架规格的限制。本文利用MATLAB仿真软件，将所需设计的包装箱尺寸、重量作为设计变量，通过软件编程求优化向量，使设计目标函数取得极值。

3 基于Matlab的优化设计

Matlab软件是一款非常优秀的数值计算和图形图像处理工具软件，其优化工具箱含有一系列优化算法函数，这些函数拓展了Matlab数字计算环境的处理能力，可以解决复杂结构的优化问题[2]。

根据铁附件结构的特点，其包装箱的优化设计是有约束的非线性规划问题。利用Matlab函数fmincon( )处理有约束的非线性多元变量的优化问题[3]，该命令的具体格式为：[x, fval, exitflag,output, lambda, grad, hessian] = fmincon (fun,x0, A, b, Aeq, beq, lb, ub, nonlcon, options)。

说明：

（1）参数中fun是目标函数，x0为初始值，x为返回的设计变量值。

（2）A和b表示线性不等式约束，A为系数矩阵，b为向量；Aeq和beq表示线性等式条件，Aeq为系数矩阵，beq为向量；lb和ub分别为优化参数x的上下界；nonlcon表示非线性约束条件；options为设置优化选项参数[3]。

（3）返回值fval为目标函数在最优解X点的函数值；exitflag为返回算法的终止标志，exitflag＞0表示优化结果收敛于解，exitflag＜0表示优化结果不收敛于解，exitflag=0表示优化超过了声明的代入函数值的次数；output为返回优化算法信息的一个数据结构；lambda是拉格朗日乘子，显示是哪个约束条件有效；grad和hessian分别表示最优解x点的梯度和Hessian矩阵值[4]。

4 优化设计实例

针对典型铁附件零件洋元进行结构优化设计（图1、图2所示），直径为D=200mm，长L=270mm。设计一种满足盛装体积在1m3的包装结构。并且要求能够实现洋元的固定，包装箱总重量小于1.5吨，能够通过叉车安放在货架之上。

图1 直径D=200洋元

图2 货架规格

根据其设计要求，其外形尺寸必须满足国家电网规定的货架安放规格，即长X，宽Y，高Z之和必须小于3.2m。试求该包装结构用料最省，安放最合理的结构参数X，Y，Z。该问题的设计目标是使包装箱在满足包装要求情况下用料最省，而包装箱材料的多少是与箱坯的面积大小直接相关的。若不计粘结边的面积，则问题可以转化为在约束条件：X＊Y＊Z=1；X+Y+Z≤3.2；X＞0，Y＞0，Z＞0。选用Matlab9.0软件来进行上述目标的设计，具体的步骤如下：

（1）首先利用 Matlab9.0的程序编辑器建立目标函数的objfun.m

function f=objfun(x)

f=2＊[X+Y]＊[X+Z];

（2）然后再建立约束条件的m文件confun.m

function [c, ceq] = confun (x)

c = [];

（3）输入优化命令

＞ ＞ x0= [1 1 1];

＞ ＞ A = [1，1，1];

＞ ＞ b = [1. 6]

＞ ＞ lb = [0; 0; 0];

＞ ＞ options = optimset ('LargeScale', 'off','Display', 'iter');

我说“：随您怎么说，说心中想说的就可以。”婆婆清了清嗓子，微笑着说：“我儿媳曾经告诉我，是一家人，就要说家人该说的话，做家人该做的事，正是坚持这一点，我们婆媳从矛盾重重走到今天的相亲相爱。”

＞ ＞ [x, fval, exitflag, output] = fmincon('objfun', x0, A, b, [], [], lb, [], 'confun', options)

完成以上步骤以后，会得到最优化的结果值：

Optimization terminated successfully：

Search direction less than 2＊ options. TolX and

maximum constraint violation is less than options. TolCon

Active Constraints：

1

X=1.45

Y=1.4

Z=0.97

fval=1.5390

exitflag=1

output=

iterations： 13

funcCount： 73

stepsize： 1

algorithm： [1x44 char]

firstorderopt： 1. 3270e - 004

cgiterations：[]

根据以上优化设计方法与程序运行结果发现，当包装箱的结构参数X=1.45m，Y=1.4m，Z=0.97m时，此时尺寸比例满足理想尺寸的比例条件2：1：2，而且材料用量fval为最小值；同时，终止迭代的错误条件exitflag=1＞0，表示优化结果收敛于解，优化是成功的。

5 仿真设计和虚拟装配

通过上述的Matlab结构优化仿真我们可以对洋元结构包装箱的外部尺寸进行最优化的设计。解决了外部尺寸设计的问题，我们可以通过NX软件对包装箱内部结构进行仿真设计和虚拟装配（图3为D200洋元虚拟装配效果图）。

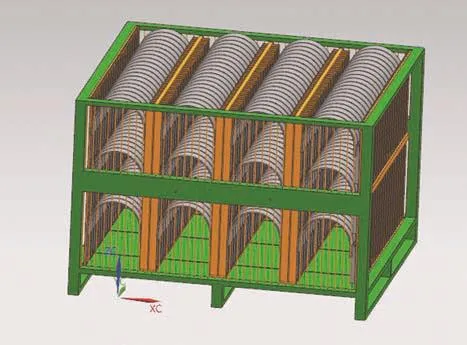
图3 D200洋元虚拟装配效果图

通过对洋元结构特点的分析，本文采用插槽式安装方法，设计的特点如下：（1）插槽式安装便于实现洋元结构的两侧固定，不会在运输和存储过程中出现掉落现象；（2）3层结构设计，最大程度上利用了箱体空间，实现包装零件数量最大化；（3）固定插槽数目设计，便于清点、发放、计数。同时通过虚拟设计可以对不同种尺寸洋元进行数量统计（表1所示）。

6 结语

根据包装容器结构尺寸优化设计的特点，分析了计算机辅助优化设计的一般流程和求解方法，选用Matlab 软件实现了设计目标。优化设计结果不仅美化了包装件的外观，而且降低了包装成本；同时，利用三维设计软件进行虚拟设计，既减少了设计者的工作量，又加快了设计速度。

[1]飞思科技产品研发中心． MATLAB6．5辅助优化计算与设计[M]．北京：电子工业出版社，2003．

[2]王德忠．包装计算机辅助设计[M]．北京：印刷工业出版社, 1999．

[3]石博强，滕贵法,等． MATLAB数学计算范例教程[M]．北京：中国铁道出版社，2004．

[4]廖敏，戴跃洪．瓦楞纸箱结构设计及其优化方法[J]．包装工程，2006，27(4)： 153-156．

[5]甘纯刚，等．瓦楞纸箱结构优化的CAD系统[J]．包装工程，2006，27(5)： 155-158．

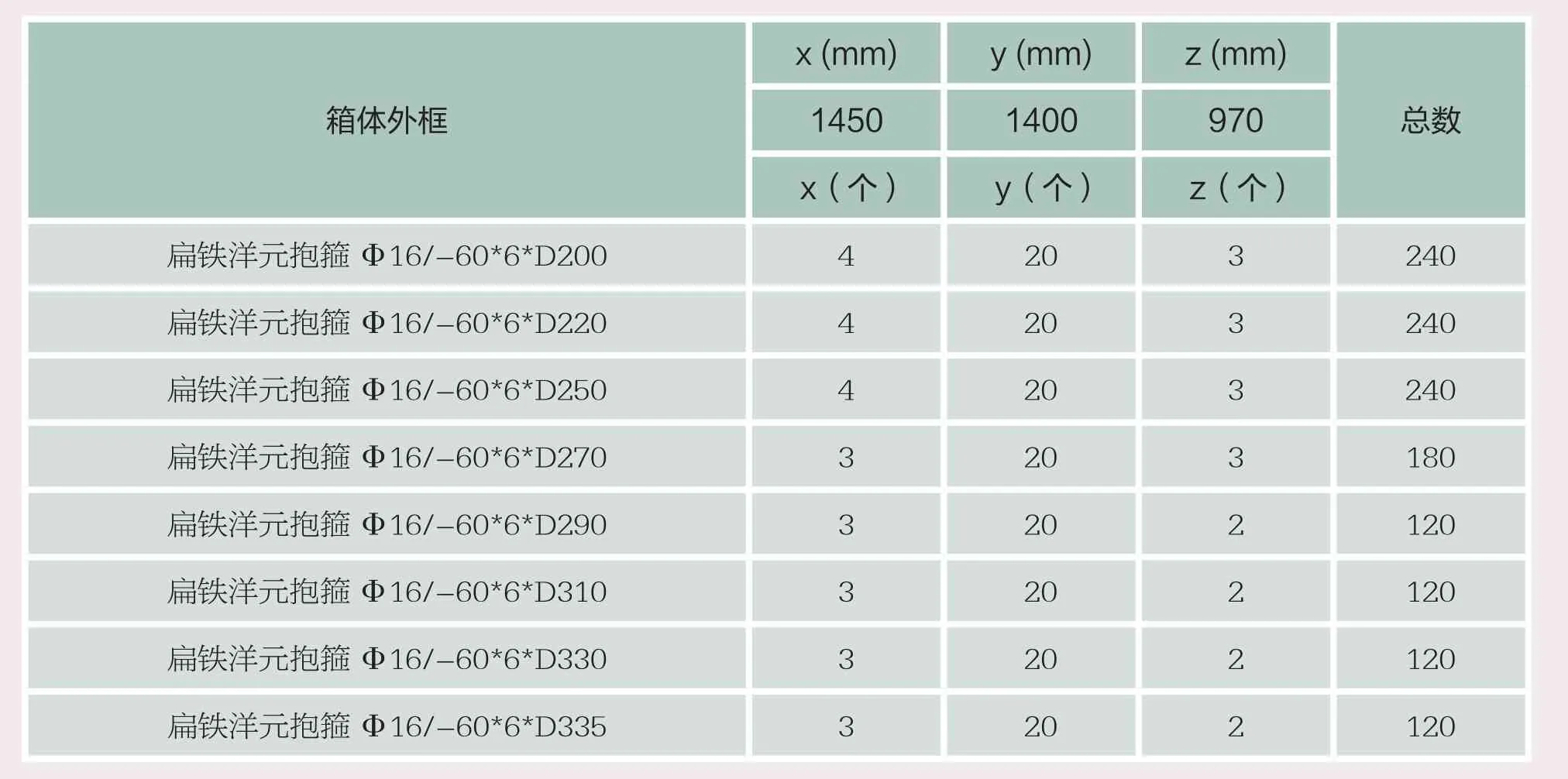
表1 包装箱尺寸和各型号安装数量