无人机自动撞网着舰轨迹自适应跟踪控制
甄子洋, 陶钢,2, 江驹, 王新华
(1.南京航空航天大学 自动化学院,南京 210016; 2.弗吉尼亚大学 电气与计算机工程学院,美国 夏洛茨维尔 22904-4743)
舰载无人机自动着舰问题一直是舰载机、无人机、飞行控制研究领域中的热点和难点。2011 年2 月,美国海军高调宣布,一款能够从航母上起飞的新型无人机——X-47B 无人侦察攻击机完成首次试飞。这一事件受到世界各国的广泛关注,标志着舰载无人机的时代已经到来。由于舰载无人机的着舰过程不仅要克服普通飞机着陆时都会面临的系统误差、环境干扰影响,还要克服甲板运动对理想着舰点的影响、舰尾气流扰动对飞行轨迹的干扰。尤其在着舰过程中要求自动着舰控制系统保持精确的着舰三维基准轨迹跟踪,才能保证最终着陆在面积狭小的甲板跑道上或回收网中,因此,精确控制与制导是舰载无人机实现成功着舰的关键技术。
国外早在20世纪50、60年代就对舰载飞机的相关技术展开研究,但是对无人机着舰技术的研究起步较晚,对相关技术成果的公开报道也很少[1-2]。国内对舰载无人机的研究刚处于起步阶段,现有研究主要集中在对舰载无人机的着舰方案设计,但对舰载无人机的精确飞行轨迹控制问题的研究鲜有报道。杨一东等[3-4]在有人驾驶舰载飞机着舰引导与控制技术研究的基础上,近年开始重点研究舰载无人机的引导与控制技术,实现了基于经典控制与非线性控制的着舰控制方案[5-8]。然而,上述控制方法的设计依赖于无人机的数学模型,而在实际应用中给设计带来一定难度。
自适应控制理论不依赖于被控对象的数学模型,对系统参数时变、外界扰动都具有很强的自适应能力与鲁棒性[9]。因此,针对舰载无人机撞网着舰三维轨迹精确跟踪问题,本文提出将模型参考自适应控制应用于舰载无人机自动撞网着舰系统中,使得飞行控制系统的设计不依赖于无人机模型参数,并且提高自动着舰系统的自适应能力。
1 无人机非线性数学模型
无人机是具有六自由度运动特性的刚体,即质心沿地面坐标系的三个移动自由度和绕机体坐标系的三个转动自由度。无人机建模时通常选取如下状态变量:速度V、迎角α、侧滑角β、滚转角速率p、俯仰角速率q、偏航角速率r、滚转角φ、俯仰角θ、偏航角ψ、在地面坐标系中的位置分量x、y、h。控制输入变量选取为:升降舵偏角δe、油门开度δT、副翼偏角δa、方向舵偏角δr。机体坐标系下的无人机动力学及运动学方程组主要包括力方程组、力矩方程组、角运动方程组和线运动方程组,具体形式可参见文献[5-6]。由方程组确定了无人机飞行状态向量XT=(V,α,β,φ,θ,ψ,p,q,r,x,y,h)与控制输入UT=(δe,δT,δa,δr)之间的非线性关系描述。
本文根据某舰载无人机的相关特征与气动参数,建立了舰载无人机的非线性全量模型。
2 下滑基准轨迹生成与引导律设计
无人机的撞网着舰过程本质上是在引导系统工作下沿着预定生成的下滑基准轨迹飞行。由此,建立如图1所示的无人机自动撞网着舰引导与控制系统结构,包括GPS引导的着舰基准轨迹生成与轨迹误差计算模块、纵侧向引导律模块以及油门、升降舵、副翼和方向舵等四个控制通道。

图1 无人机自动撞网着舰引导与控制系统结构Fig.1 Net landing guidance and control system structure of UAV
2.1 下滑基准轨迹生成与轨迹误差计算
不同的无人机撞网着舰引导装置有不同的基准轨迹生成方法。GPS系统是在以理想着舰点为原点的地面坐标系下引导飞机着舰的,所以建立的撞网基准轨迹是基于该坐标系的。
设飞机的预定下滑角为γc、下滑速度为Vc、着舰时间为td,舰船以恒定速度VS保持航向角为ψS0航行,回收网平面与舰船中心线的夹角为λac,则无人机开始着舰时距离理想着舰点的斜距RA=Vtd。由此可建立无人机撞网着舰的三维基准轨迹表示为
(1)
式中:XEATDc为理想前向距离,YEATDc为理想侧向距离,-ZEATDc为理想高度。
设GPS测量得到无人机的绝对位置再与舰船绝对位置进行对比,得到以理想着舰点为原点的地面坐标系下的无人机实际位置为XEATD(t)、YEATD(t)、ZEATD(t),于是无人机与基准下滑轨迹的高度差和侧向偏距分别为
Her(t)=-[ZEATDc(t)-ZEATD(t)]
(2)
yer(t)=YEATDc(t)-YEATD(t)
(3)
2.2 纵侧向引导律设计
引导系统将无人机着舰过程的三维基准轨迹跟踪偏差信号转化为姿态角指令信号,属于轨迹控制回路,作为姿态控制回路的外回路。纵向引导是以俯仰姿态作为内回路,通过飞机高度信息与期望高度信号求差,得到高度误差信号,通过抑制高度误差来实现飞行高度的控制。侧向引导律的作用是通过将期望侧偏信号与实际侧偏信号相减得到误差信号,消除这一误差信号,不断修正飞行航迹。
为了更快速、准确地消除静差,并且使引导律在滤去传感器噪声的同时具有一定的稳定裕度并且具有足够带宽,在设计时加入α-β滤波器。α-β滤波器、α1滤波器、α2滤波器的传递函数表达式为
式中T为采样周期。

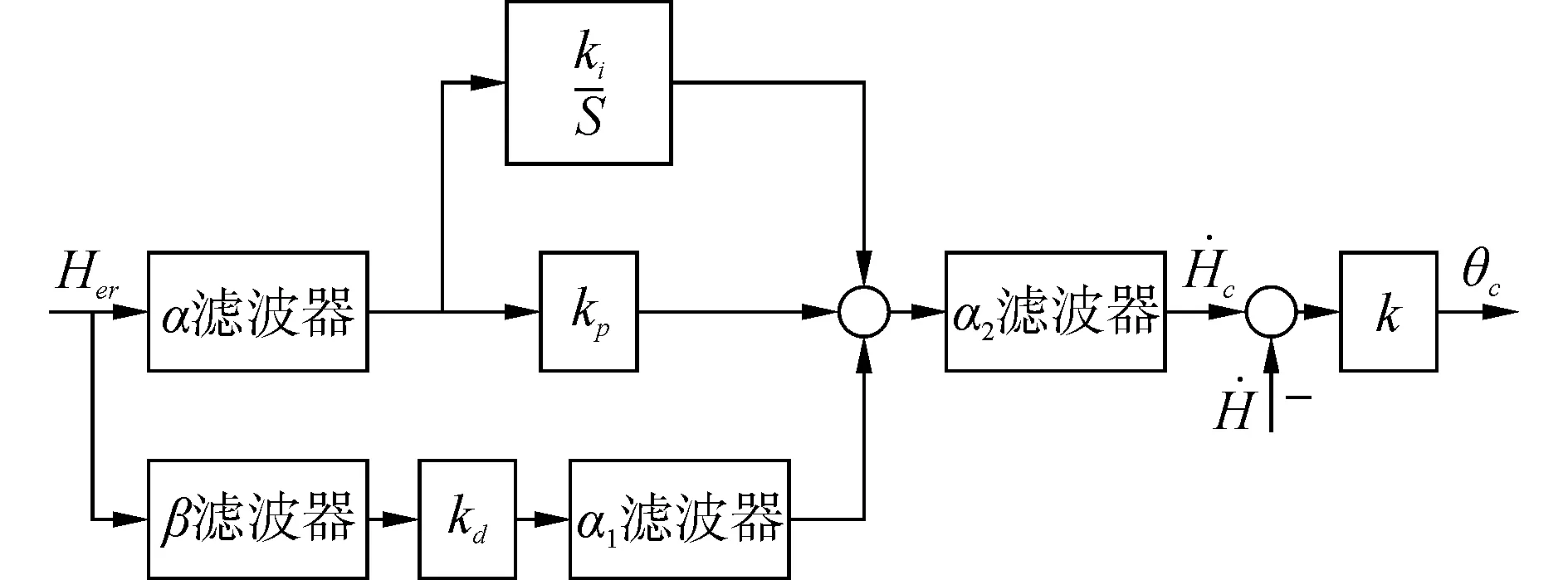
图2 纵向引导律原理框图Fig.2 Block diagram of longitudinal guidance law
3 自适应飞行控制律设计
飞行控制回路分四个通道:油门通道、升降舵通道、副翼通道、方向舵通道。下面基于SISO模型参考自适应控制方法,基于参数未知的无人机线性模型,设计每个通道的自适应控制律。
3.1 模型参考自适应控制理论
考虑SISO线性定常系统:

(4)
式中:A∈Rn×n,b∈Rn×1,c∈R1×n。
假设:(i)系统是可镇定和可检测;(ii)系统传递函数零点多项式是稳定多项式并且阶次为m。由此选择如下参考模型:
(5)
式中:Pm(s)为稳定的首一多项式,且阶次为(n-m),n为传递函数极点多项式阶次,r(t)为参考输入。
在系统参数A、b、c已知的情况下,理想控制律设计为
(6)
(7)

ε(t)=ρ*(K(t)-K*)Tζ(t)+(ρ(t)-ρ*)ξ(t)
(8)
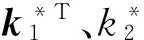
基于下降梯度法设计参数估计的自适应律为
(9)
(10)

定理1[9]针对SISO线性时不变系统(4),在模型参数a、b、c未知的情况下,满足假设条件(i)~(ii),设计稳定的参考模型(5),设计状态反馈输出跟踪自适应控制律(7)、(9)、(10),则闭环系统输出渐近跟踪参考模型输出,即满足:
(11)

(12)
同时,闭环系统所有信号都是有界的。
3.2 飞机姿态自适应控制律设计
无人机的纵向运动可以分解为短周期运动模态和长周期运动模态两种。从纵向状态空间模型中的数值元素可以看出,速度对油门开度的变化较为敏感,而迎角受油门开度影响较小,说明油门开度主要用来控制空速。同理,由其他数值元素大小可推断:升降舵主要控制俯仰运动,副翼主要影响滚转运动,方向舵主要影响侧滑角,用来改善荷兰滚运动的阻尼,起到辅助横侧向控制的作用。
针对多变量系统采用分散控制的合理性问题,文献[10]提出了基于相对增益阵列(relative gain array, RGA)的系统耦合程度判别方法。通过RGA的计算表明,各通道之间的耦合程度相对较小,所以分散控制方法适用于此应用问题,即无人机的纵向运动可以分解为升降舵控制俯仰角通道与油门控制速度通道,横侧向运动可以分解为副翼控制滚转角通道与方向舵控制侧滑角通道。
因此,利用SISO模型参考自适应控制方法分别设计四个通道的控制律是可行的。具体步骤如下。
1)升降舵通道控制律。
该通道的状态空间模型表示为
(13)

(14)
根据模型阶次,设计二阶参考模型:
式中p0、p1是配置的稳定极点。
引入辅助变量
ω(t)=(Δα,Δq,Δθ,Δθc)T
由此,俯仰姿态自适应控制律设计为
(15)
式中k1(t)、k2(t)根据自适应律(9)~(10)在线调整。
2)油门通道控制律。
该通道的状态空间模型表示为
(16)
根据模型阶次,设计一阶参考模型:
式中p3是配置的稳定极点。
引入辅助变量:
由此,速度自适应控制律设计为
ΔδT(t)=k1(t)ΔV(t)+k2(t)ΔVc(t)
(17)
式中k1(t)、k2(t)根据自适应律(9)、(10)在线调整。
3)副翼通道控制律。
该通道的状态空间模型表示为
(18)
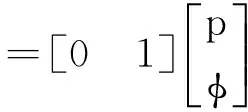
(19)
根据模型阶次,设计一阶参考模型:
φc](t)
式中p4是配置的稳定极点。
引入辅助变量:
滚转姿态自适应控制律设计为
φc(t)
(20)
式中k1(t)、k2(t)根据自适应律(9)、(10)在线调整。
4)方向舵通道控制律。
该通道的状态空间模型表示为
(21)

(22)
根据模型阶次,设计一阶参考模型:
式中p5是配置的稳定极点。
引入辅助变量:
由此,侧滑角自适应控制律设计为
(23)
式中k1(t)根据自适应律(9)、(10)在线调整。
上述四个通道的控制律是针对各个通道的SISO线性系统设计的,该设计并不基于无人机的线性化模型的参数,即是在系统参数未知的情况下。
4 数值仿真研究
仿真中,基于“银狐”无人机的气动数据建立无人机非线性全量模型[6]。无人机与理想着舰点的初始相对位置为:前向距离1 989.7 m,侧向距离174.1 m,高度104.7 m。无人机的初始平衡状态为:速度20 m/s,迎角3.959°,俯仰角0.458°。无人机对飞行控制系统的要求是速度保持在平衡态,俯仰角和滚转角跟踪引导系统发出的指令信号,侧滑角消除。图3~6分别表示下滑高度、侧向距离、下滑速度、俯仰角、滚转角、侧滑角的跟踪响应及升降舵、油门、副翼和方向舵响应曲线。

图3 下滑高度Fig.3 Glide height

图4 侧向轨迹Fig.4 Lateral path

图5 各变量跟踪响应Fig.5 Response of the variales
从仿真结果看出,无人机在撞网着舰过程中,对三维下滑轨迹的跟踪精度较高,尤其是高度、侧向距离、跟踪误差着舰收敛、着舰时刻达到很高的精度。同时,着舰过程无人机的速度保持得很好,俯仰角和滚转角都很好地跟踪了引导系统给出的指令信号,侧滑角控制接近于零。三个气动舵面的偏转以及油门开度最终也都趋于稳定,即无人机状态和控制量都趋于稳态值,即无人机处于平衡运动状态,从而实现了稳定下滑着舰。

图6 操纵响应Fig.6 Response
5 结论
1)基于SISO状态反馈输出跟踪模型参考自适应控制方法,设计了无人机自适应着舰控制系统,非线性无人机模型验证了自适应控制技术在无人机自动着舰问题中的可行性和有效性;
2)与常规的线性控制和非线性控制方法相比,自适应控制不依赖于模型参数,适用于模型参数未知的实际系统,且控制律结构形式较为简单,能够在线调整控制参数,具有较强的鲁棒性能,在实际工程中具有很好的应用前景;
在考虑甲板运动跟踪与抑制舰尾气流等实际着舰环境因素下,如何设计自适应飞行控制系统,实现复杂环境下的无人机精确着舰,是下一步的研究重点。
[1] Anon. Naval interest in shipborne unmanned air vehicles [J]. Naval architect, 1997: 45-46.
[2] PERRY J D. Navy unmanned air systems 1915-2011 [C]//Proceedings of AIAA Centennial of Naval Aviation Forum “100 Years of Achievement and Progress”. [S.l.], 2011.
[3] 杨一栋. 舰载飞机着舰引导与控制[M]. 北京:国防工业出版社, 2006.
YANG Yidong. Carrier landing guidance and control of carrier-based aircraft[M]. Beijing: National Defense Industry Press, 2006.
[4] 甄子洋, 王新华, 江驹, 等. 舰载机自动着舰引导与控制[J]. 航空学报, 2017, 38(2): 1-22.
ZHEN Ziyang, WANG Xinhua, JIANG Ju, et al. Research progress in guidance and control of automatic carrier landing of carrier-based aircraft[J]. Acta aeronautica ET astronautica sinica, 2017, 38(2): 1-22.
[5] 杨一栋, 甄子洋, 徐佳龙, 等. 无人机着舰制导与控制[M]. 北京: 国防工业出版社, 2013.
YANG Yidong, ZHEN Ziyang, XU Jialong, et al. UAV carrier landing guidance and control[M]. Beijing: National Defense Industry Press, 2013.
[6] 李若兰, 甄子洋, 龚华军. 基于趋近律滑模最优控制的无人机撞网回收轨迹控制[J]. 电光与控制, 2014, 21(9): 58-60, 84.
LI Ruolan, ZHEN Ziyang, GONG Huajun. Trajectory control of a UAV during net recovery based on sliding mode control and optimal control[J]. Electronics optics and control, 2014, 21(9): 58-60, 84.
[7] ZHENG F Y, GONG H J, ZHEN Z Y. Adaptive constraint backstepping fault tolerant control for small carrier UAV with uncertain parameters[J]. Proceedings of the institution of mechanical engineers, Part G: journal of aerospace engineering, 2016, 230: 407-425.
[8] ZHENG F Y, ZHEN Z Y, GONG H J. Observer-based backstepping longitudinal control for carrier-based UAV with actuator faults[J]. Journal of systems engineering and electronics, 2017, 28(2): 322-337.
[9] TAO G. Adaptive control design and analysis[M]. [S.l.]:Wiley-Interscience, 2003.
[10] GOODWIN G C, GRAEBE S F, SALGADO M E. Control system design[M]. Upper Saddle River: Prentice-Hall, 2001.
本文引用格式:
甄子洋, 陶钢, 江驹, 等. 无人机自动撞网着舰轨迹自适应跟踪控制[J]. 哈尔滨工程大学学报, 2017, 38(12): 1922-1927.
ZHEN Ziyang, TAO Gang, JIANG Ju, et al. Adaptive tracking control of automatic net landing trajectory for carrier-based UAV[J]. Journal of Harbin Engineering University, 2017, 38(12): 1922-1927.

