波浪中KVLCC2运动与阻力增加的CFD计算及分析
曹阳, 朱仁传, 蒋银, 洪亮
(上海交通大学 船舶海洋与建筑工程学院,海洋工程国家重点实验室,高新船舶与深海开发装备协同创新中心,上海 200240)
船舶在波浪上的运动与阻力增加一直是船舶与海洋工程领域研究的热点,准确预报船舶在波浪上的运动是船舶在水上航行、作业安全性和舒适性的基础,船舶波浪增阻在船型优化乃至航线优化问题中是经济性的重要参数指标。
目前,关于波浪中航行船舶运动与增阻研究主要有船模试验(experimental fluid mechanics, EFD)、基于势流理论的理论计算[1]和考虑黏性的计算流体力学(CFD)数值模拟等方法。基于势流理论的方法主要有切片法、三维面元法等,相对简单且计算效率高,但势流理论没有考虑粘性的影响,且对诸如船体大幅度运动、波浪破碎等强非线性因素难以适用。而船模试验往往需要进行费时费力的系列模型试验,成本较高,试验频率也有限制,由于仪器设备和测试技术等方面的原因,目前还难以准确地监测出船体周围复杂流场的信息。
CFD方法由于考虑了粘性能对非线性问题作较为准确的数值模拟,随着计算机计算能力的提高日渐成为求解船舶与海洋工程水动力问题的一种重要手段,近年来已经取得了一系列重要的进展。Carrica等[2-3]利用重叠网格采用单相 level-set方法捕捉自由面,考虑了纵摇和垂荡两个自由度,对船模DTMB 5512在波浪中的自由运动的进行了数值模拟。GUO等[4-5]研究了KVLCC2在短波中的增阻,验证了Faltinsen渐进公式预报船舶在短波中增阻的准确性,同时还对KVLCC2的耐波性做了研究,并分析了波浪对螺旋桨盘面处流场的影响。Sadat-Hosseini等[6]考虑纵荡的影响,数值预报超大型油轮KVLCC2在不同波长迎浪工况下的波浪增阻和运动响应,结果表明纵荡对纵摇和波浪增阻几乎没有影响。国内基于CFD方法关于船舶在波浪上运动与增阻的研究也取得了很多成果。方昭昭等[7-9]基于CFD方法建立了数值波浪水池,使用Fluent软件结合动网格技术对不同航速顶浪航行的Wigley-III型船模的水动力系数、垂荡、纵摇、波浪增阻等进行了数值计算,结果与实验结果[10]吻合较好。沈志荣等[11-12]利用基于开源代码OpenFOAM平台开发计算分析了Wigley-III 型、DTMB5415、S175等船型在迎浪中的运动响应以及波浪增阻。
CFD模拟船体运动需要使用动网格技术,涉及到网格的再生与变形,若船体运动响应较大,网格畸变容易引发数值计算发散或是计算结果误差大。重叠网格方法对于复杂曲面离散以及物体大幅运动具有无可比拟的优势,能方便处理复杂三维船体曲面,容易保证局部网格质量,动态重叠网格在处理结构物具有大幅运动的绕流问题时不需要网格再生,提高了动态网格处理效率。
本文基于粘性流理论使用CFD软件建立了数值波浪水池并结合重叠网格方法,对航速为1.047 m/s(Fn=0.142 )缩尺比为58的KVLCC2模型在波浪上的运动进行了数值模拟,同时研究了KVLCC2在波浪中的阻力增加,分析了波阻成分。
1 数值波浪水池与重叠网格技术
本文的数值模拟是在一个三维数值波浪水池中进行,水池尺度随入射波长的不同而不同,在出口处和两侧边界附近设有人工阻尼消波区,消波区段约为2倍波长,船侧消波区距船舷侧约1倍船长,水池前端距船艏约1倍波长,尾端消波区距船艉约1倍波长。数值波浪水池及坐标系如图1所示,固定坐标系O0x0y0z0原点位于船体中纵剖面、中横剖面以及静水面交点,x0轴指向船艏,y0轴指向船舷左侧,z0轴垂直向上;参考坐标系Oxyz原点位于重心处,各坐标轴方向与固定坐标系对应一致。
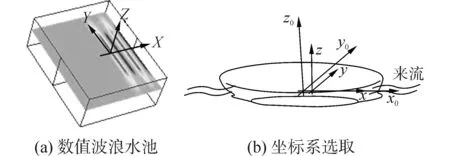
图1 数值波浪水池及坐标系Fig.1 Numerical wave tank and the coordinate system
1.1 流体控制方程
整个流场以连续性方程和N-S方程为控制方程:
(1)
(2)

湍流模式为SSTk-ω两方程模型,其控制方程为
(i=1,2,3)
(3)
式中:Γk、Γω为湍动能k和比耗散率ω的有效扩散系数,Yk、Yω为k和ω湍流耗散,Gk为平均速度梯度引起k的产生项,Gω为ω的产生项,Sω为交叉扩散项。
流体体积输运方程为
(4)
本文在后面的数值计算中采用有限体积法离散上述控制方程,对流项使用二阶迎风插值格式,扩散项的离散采用中心差分格式,应用SIMPLE算法分离式求解;考虑重力影响,使用多重网格方法迭代求解离散代数方程组。
1.2 数值造波与消波
船舶在波浪中航行时的运动模拟,需要提供满足计算要求的波浪环境,即首先要构建数值波浪水池,本文采用速度边界法造波。假定波浪沿x轴负方向传播,根据波浪理论,参考坐标系下入射势、遭遇频率以及波面表达式为
(5)
参考坐标系下流体质点的速度表达式为
(6)
在数值波浪水池的尾部设置有人工阻尼消波区,其长度约为入射波长的2倍。在消波区,对流体质点垂向速度做强迫衰减,为保证流动的连续性,水平速度不做衰减处理[13]。强迫衰减的公式为
式中:wr(x,y,z;t)为衰减后的垂向速度;μ(x,z)为衰减函数;xs≤x≤xe,zb≤z≤zf;下标s和e分别代表阻尼区沿x方向的起点和终点;b和f分别代表沿z方向的底部和自由面;α为阻尼控制参数。
当流场中有船体存在时,还要在数值波浪水池的侧面设置人工阻尼消波区,同样只对流体质点垂向速度做强迫衰减,强迫衰减公式为
式中:η(y,z)为衰减函数;yw≤y≤yn,zb≤z≤zf;下标w和n分别代表阻尼区沿y方向的起点和终点;b和f分别代表沿z方向的底部和自由面;α为阻尼控制参数。
1.3 重叠网格技术
为更好地模拟船体在波浪上的运动,本文采用重叠网格技术。重叠网格,也叫嵌合体网格,是一种区域分割与网格组合的策略,涉及到两种区域:背景区域和重叠区域,两种区域以任意方式叠加。如图2所示,整个流场称之为背景区域,该区域生成的网格为背景网格;包裹着船体随船体做刚性运动的小区域为重叠区域,这个区域产生的网格称为重叠网格,两套网格之间通过交界面来识别。

图2 重叠网格图解Fig.2 The sketch of multi-region
重叠网格技术将网格分为有效单元和无效单元。只有有效单元参与离散控制方程的求解,无效单元指的是重叠区域内被挖去的背景网格,不参与控制方程的求解,当重叠区域随船体做刚性运动时背景网格中的部分有效单元和无效单元会相互转化。重叠网格与背景网格的信息交换通过受者单元和贡献单元之间插值来完成的,一般采用拉格朗日插值的思想,进行线性插值,具有以下形式[14]:
φrec=∑ξiφi
(11)
式中:φrec为受者单元的流动物理量;φi为其相邻贡献单元的流动物理量;对于二维问题,ξi为以相邻贡献单元中心为顶点组成三角形对应的形函数;如果是三维问题,ξi是四面体所对应的形函数,该四面体的顶点由相邻贡献单元的中心组成。
1.4 船体运动方程
本文数值模拟了KVLCC2在长波中迎浪航行工况下的运动,纵荡运动较小且对其他运动以及波浪增阻几乎没有影响,此处只考虑垂荡和纵摇两个自由度,其运动方程为
(12)

为避免作用于船体的力或力矩过大造成船体剧烈的运动,在初始时给船体受到的力和力矩乘上一个阻尼函数fr,定义如下
其中,是时刻t时相关矩阵C的估计。我们可以使用指数加权或者滑动加窗的来估计。其中,关于的最简单的选择就是在最小均方算法中的。因此,信号子空间的表达式可更新为:
(13)
式中:ts为船体可以开始运动的时间,tr为船体开始运动后作用于船体的力和力矩受到人工抑制的时间。
2 波浪中航行船舶的数值模拟
本文数值模拟的是迎浪工况,流场关于船体中纵剖面对称,计算域取流场的一半即可。数值模拟计算主要考虑船体垂荡和纵摇两个自由度,部分短波工况,也采用固定模进行了数值模拟。
2.1 船体几何参数
KVLCC2是II型MOERI(maritime and ocean engineering research institute)油轮,相较于广泛研究的Wigley、S60以及S175船模具有更复杂的船体外形,其主要船型参数如表1所示,各站横剖面如图3所示。
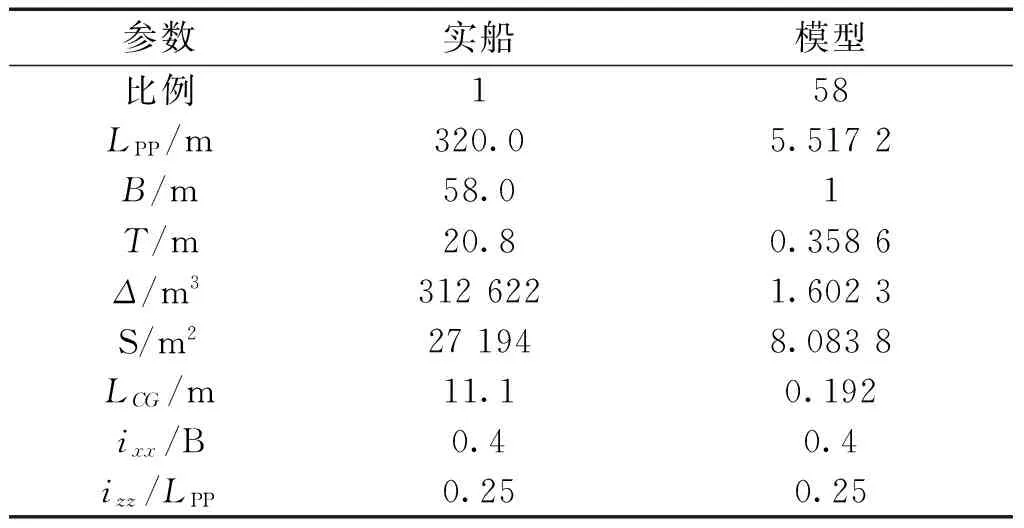
表1 KVLCC2及模型主尺度
2.2 边界条件与网格划分
波浪中航行船舶水动力计算域的边界条件设定如下:前端及上下面均为速度入口;左右为对称边界条件;长波时尾端采用压力出口,短波时尾端可以视为远场,用速度入口作为边界条件;船体设定为壁面边界条件。

图3 KVLCC2各站横剖面图Fig.3 The cross section of KVLCC2
计算区域网格的划分主要从如下几个方面考虑:沿波浪传播方向保证足够数量的网格,以避免数值耗散引起的波浪幅值的沿程衰减;垂向沿自由面附近要保证足够数量的网格,以精准捕捉自由液面;为准确捕捉尾迹,在开尔文兴波区范围内也进行了网格加密;在流场变化比较剧烈的地方如球鼻艏以及船艉附近要进行网格加密;为了获得准确的船体周围流场信息,船体附近网格划分较远场网格划分应精细一些;在消波区,保证网格平缓过渡的情况下适当拉大x和y方向网格的尺度,既减少计算量又可以起到数值消波的作用。船体壁面设置5层边界层网格,y+取50左右,为减少网格量,甲板不设边界层。
主要工况计算所用网格参数及时间步如表2所示,计算所用网格划分如图4所示。
2.3 数值模拟结果的处理
本文采用傅里叶级数展开法,使用傅里叶级数对数值模拟得到的垂荡、纵摇以及阻力时历曲线进行拟合。
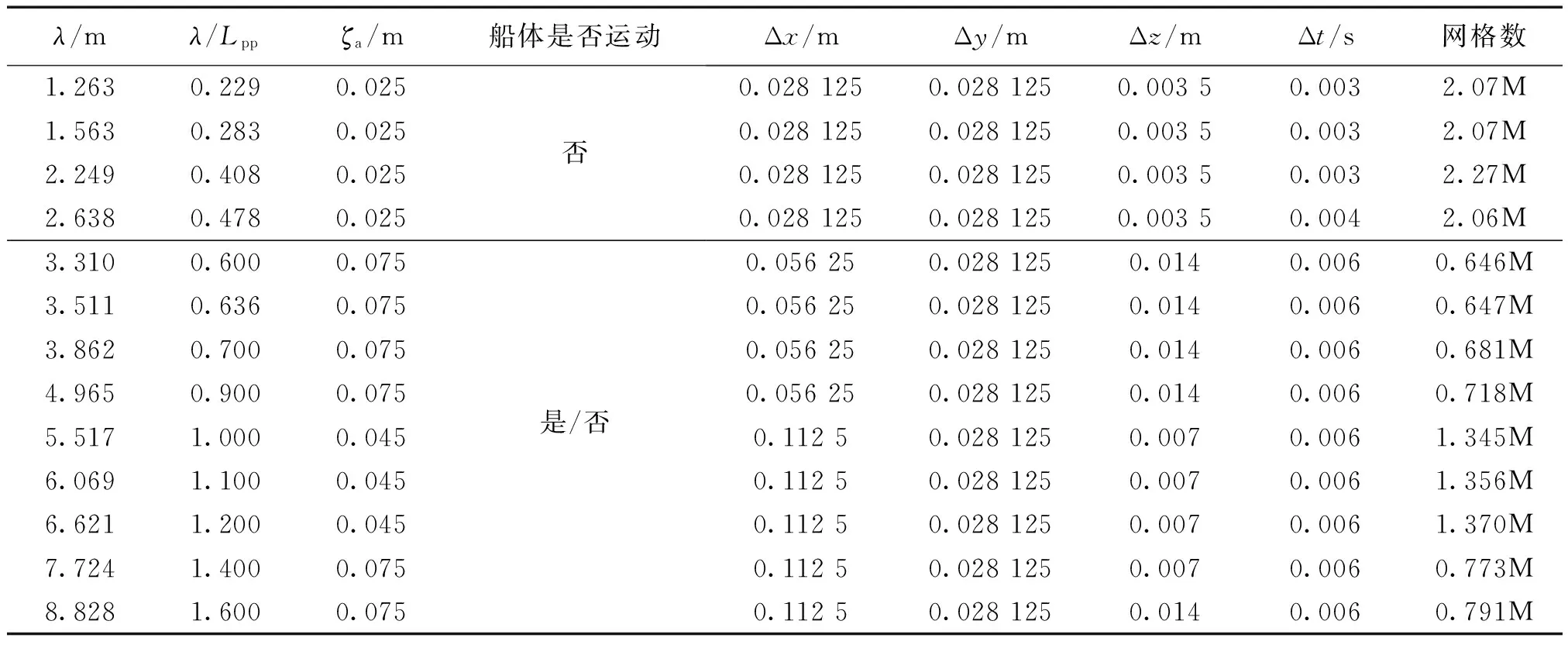
表2 主要工况及计算所用网格参数(Fn=0.142)Table 2 The main conditions simulated and the parameters used for mesh generation(Fn=0.142)
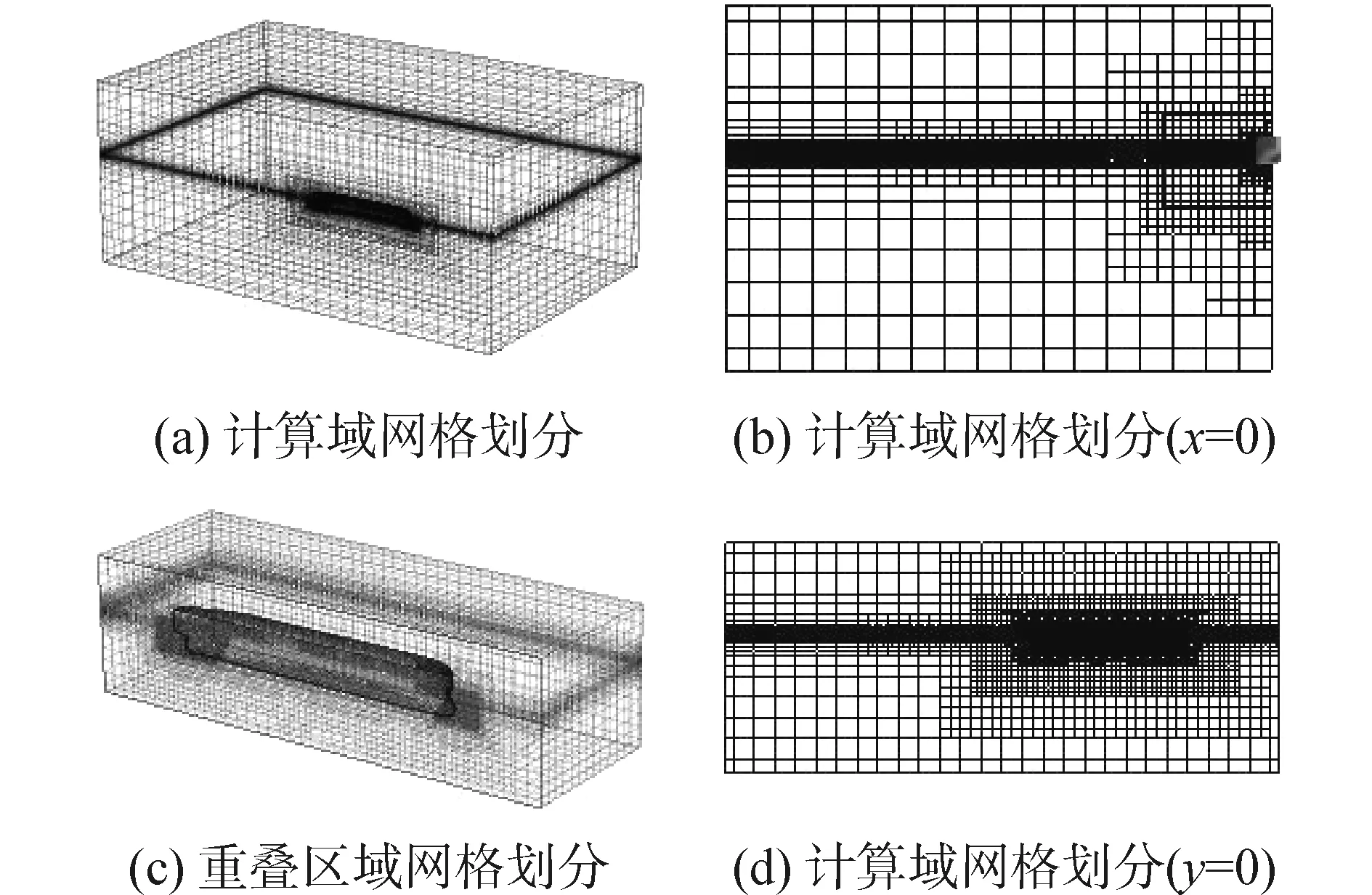
图4 计算域网格划分Fig.4 Mesh used for numerical simulation
Rwave=Rt+R1stsin(wet+γ1)+…
(14)
式中:Rwave为波浪力;ωe为遭遇频率;Rt为拟合得到的傅里叶级数的定常值,即平均波浪力;R1st为一阶波浪力幅值;γ1为一阶波浪力的相位。
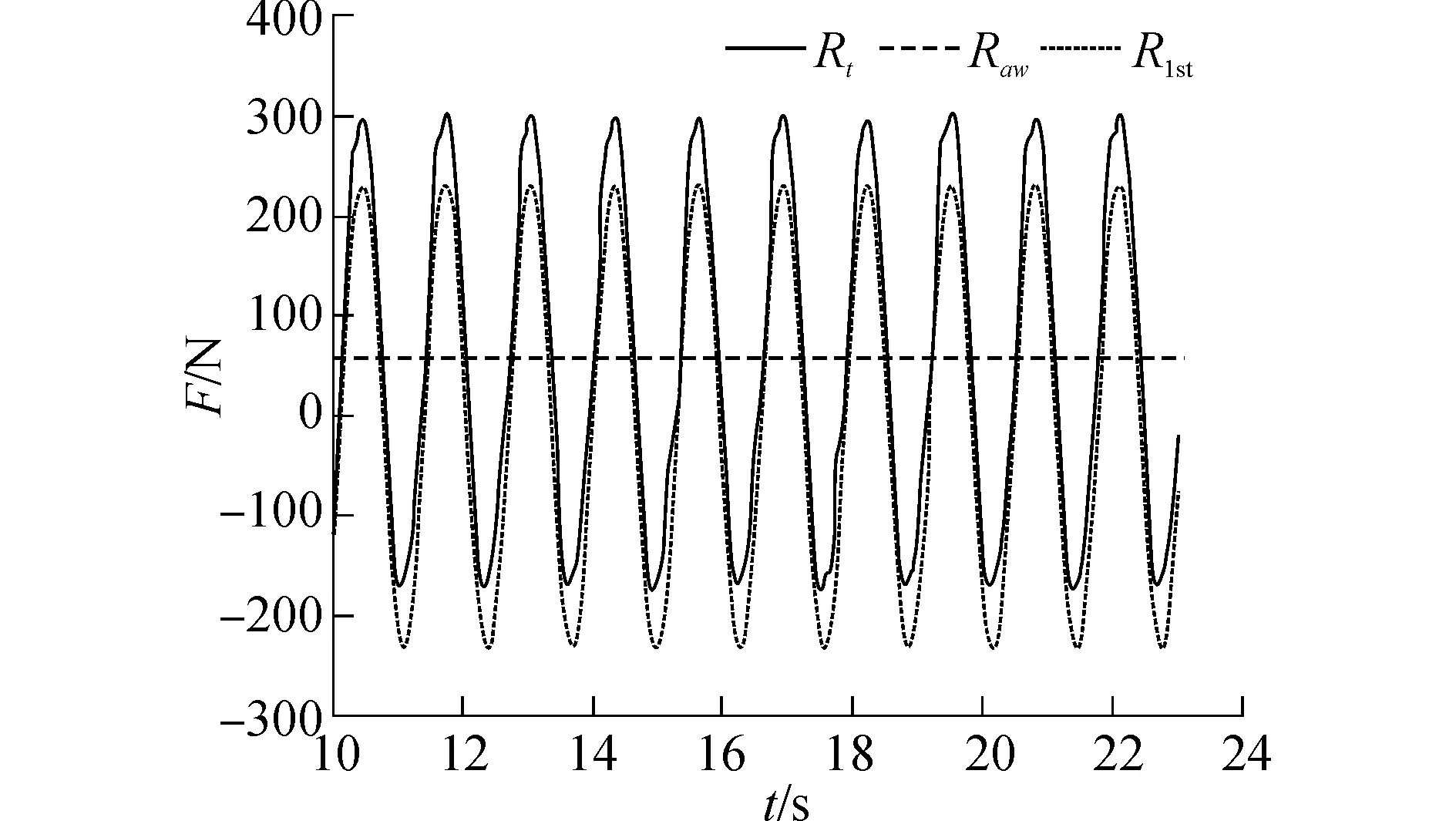
图5 傅里叶级数展开法示例(Fn=0.142、L=4.965 m、ξa=0.075 m)Fig.5 Example of Fourier series expansion method (Fn=0.142,L=4.965 m,ζa=0.075 m)

3 KVLCC2在波浪中的运动与增阻
势流理论使用的是由上海交通大学水动力学实验室基于二维势流理论开发的切片程序计算的结果,实验结果取自大阪大学(OU)、意大利船舶研究所(INSEAN)以及挪威科技大学(NTNU)三家单位发表在相关文献上的实验数据[15]。
3.1 垂荡和纵摇
采用傅里叶级数拟合运动时历曲线分析可得不同频率遭遇波下船体运动响应的幅值和相位。KVLCC2垂荡和纵摇幅值分别按式(15)进行无因次化,其幅频响应曲线如图6、7所示。
(15)
式中:ξa为遭遇波波幅,K为波数,X3和X5分别为垂荡和纵摇的幅值。
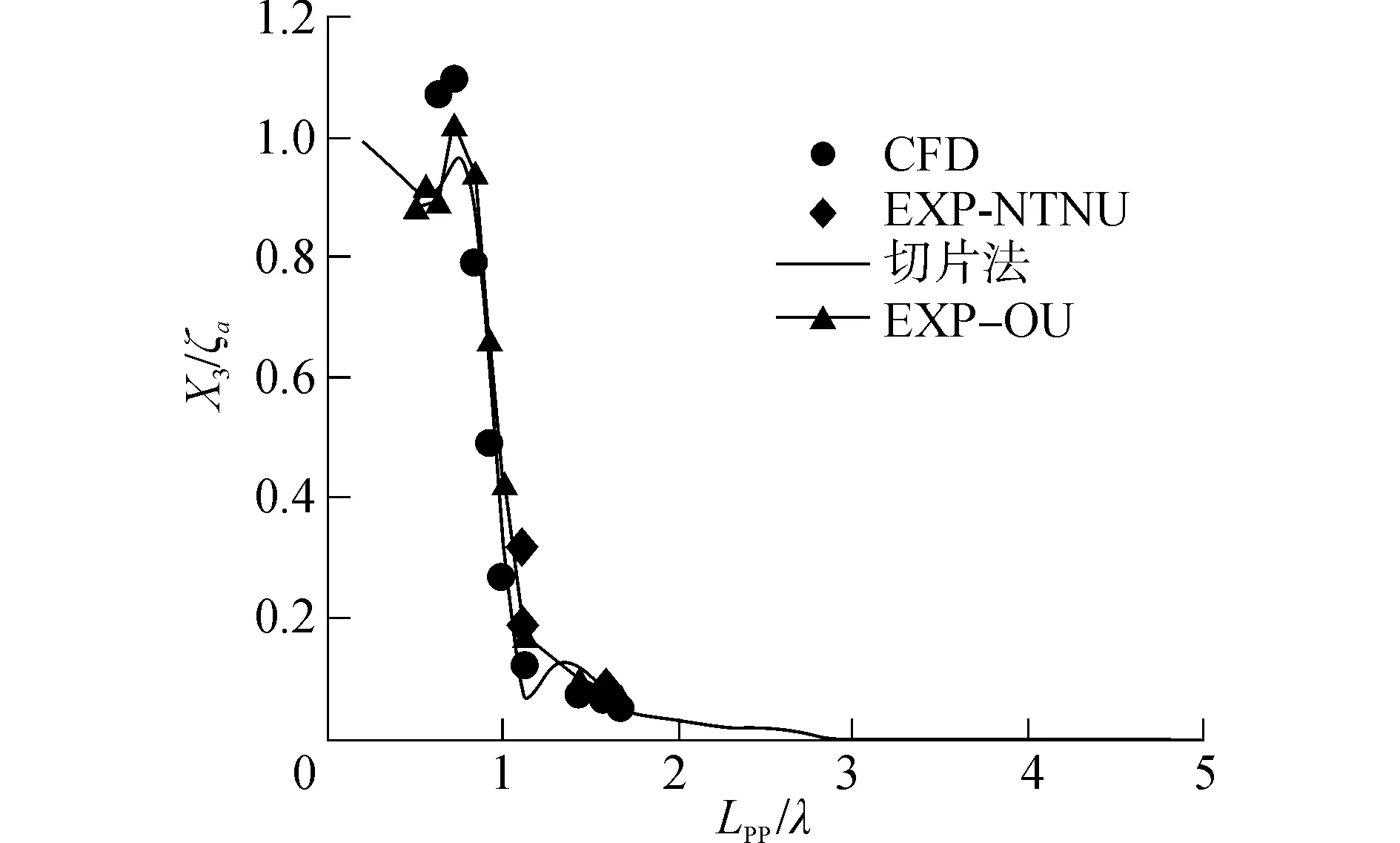
图6 Fn=0.142时KVLCC2的垂荡幅值Fig.6 RAO heave of KVLCC2 in head waves, Fn=0.142

图7 Fn=0.142时KVLCC2的纵摇幅值Fig.7 RAO pitch of KVLCC2 in head waves, Fn=0.142
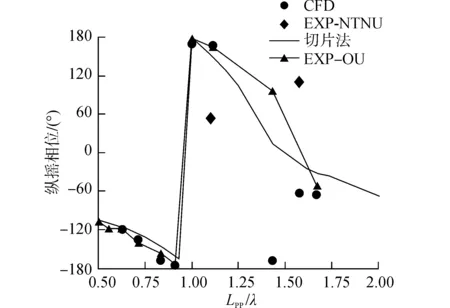
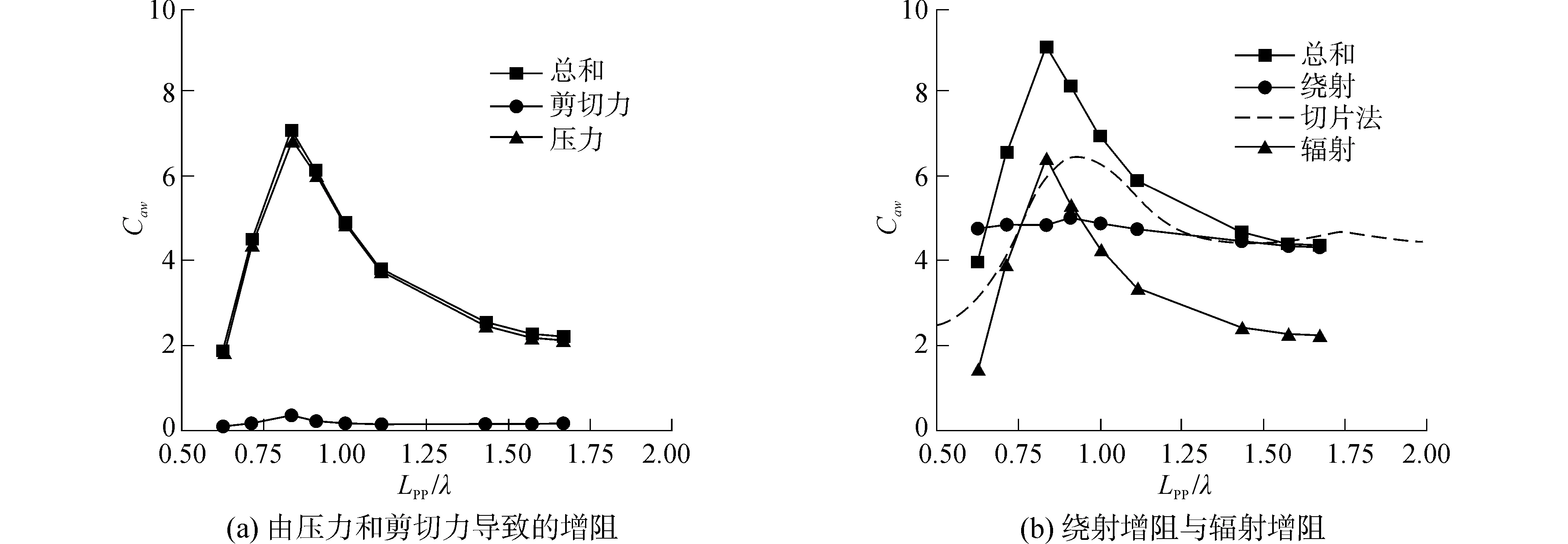
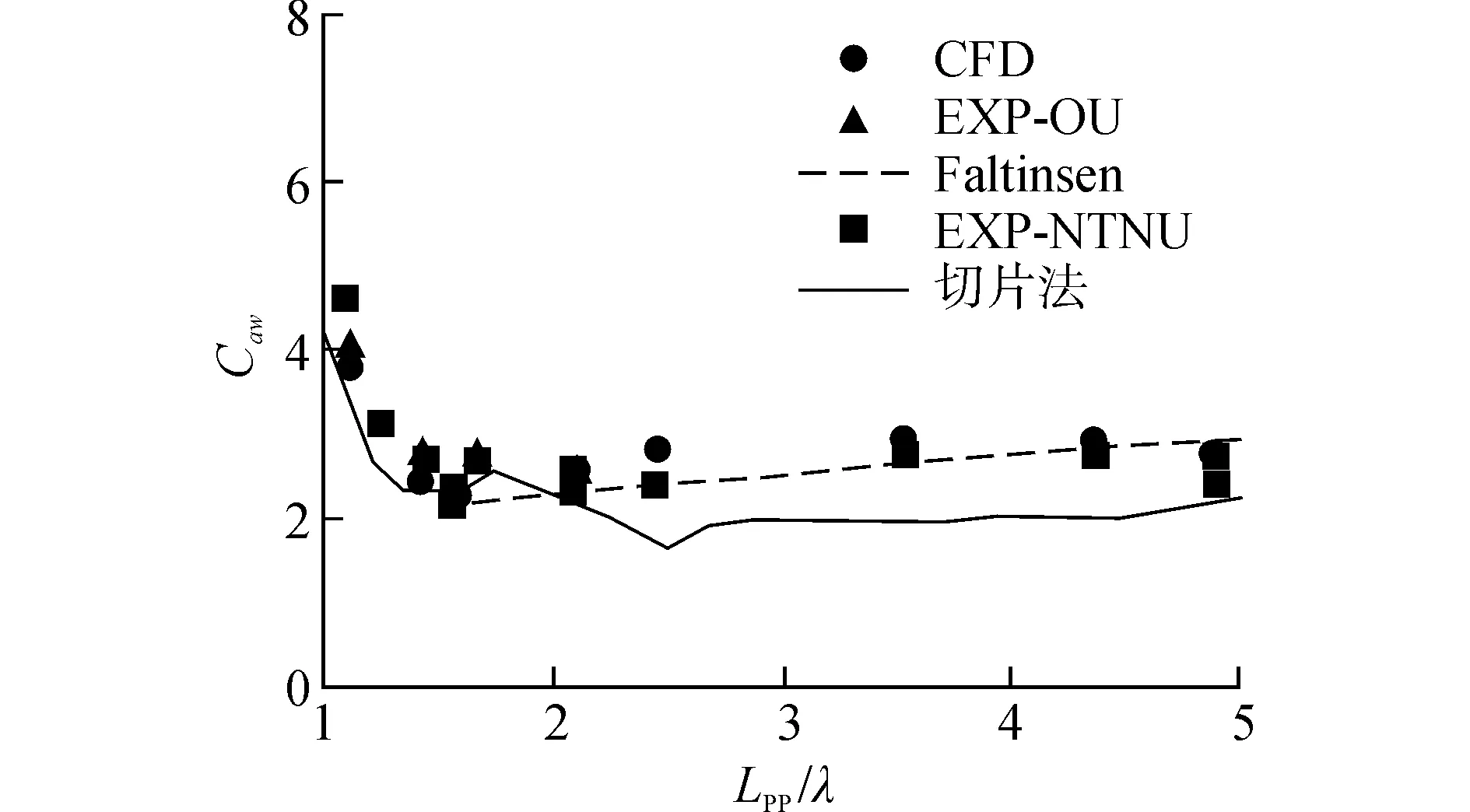
从图6、7中可以看出,数值模拟的结果与实验结果整体吻合较好。在0.7 图8、9给出了KVLCC2垂荡和纵摇运动与遭遇波的相对相位随Lpp/λ变化情况,数值模拟的结果同实验结果整体符合较好。1.0 图8 Fn=0.142时KVLCC2的垂荡相位Fig.8 Heave phase of KVLCC2 in head waves, Fn=0.142 图9 Fn=0.142时KVLCC2的纵摇相位Fig.9 Pitch phase of KVLCC2 in head waves, Fn=0.142 (16) 图10为Fn=0.142 时KVLCC2波浪增阻的CFD模拟结果与切片法计算结果以及实验结果的对比,其中切片法采用辐射能量法计算波浪增阻,可以看到,CFD模拟的结果同实验结果吻合较好。切片法计算的增阻值整体上小于实验值,增阻幅值同实验值差异较大,主要原因是:势流方法没有考虑粘性的影响,流体的粘性也贡献了一部分增阻;本文势流切片方法采用辐射能量法计算波浪增阻,没有考虑绕射对增阻的贡献。 图10 Fn=0.142时KVLCC2在波浪上的增阻Fig.10 Added resistance coefficient of KVLCC2 in head waves, Fn=0.142 从作用力方向分析,总的波浪增阻由压力增阻、摩擦增阻两部分组成;从物理问题角度出发,波浪增阻又可分解为辐射增阻和绕射增阻。图11给出了遭遇频率对增阻成分的影响。由图11(a)可以看到,在全波长范围内波浪增阻基本上由压力增阻贡献,由摩擦力引起的增阻很小。从图11(b)可以看出,波长对绕射增阻影响较小,辐射增阻在Lpp/λ>1.3时趋于0,在长波范围,辐射增阻随着波长的增大而减小。 由上述分析可知,船舶在短波中的增阻主要由绕射增阻贡献,Lpp/λ>1.3时辐射增阻可以忽略不计,现在对KVLCC2在短波中的增阻成分作进一步验证。 图12中,CFD方法计算的是Fn=0.142 时KVLCC2固定模在短波中的增阻值,实验测量的是Fn=0.142 时KVLCC2自由模在短波中的增阻值。其中“Faltinsen”是用Faltinsen的渐近公式[14]计算得到的波浪增阻,顶浪工况下渐进公式为 (17) 式中:C_l表示非遮蔽水线,ω0是波浪的频率,θ是水线的切线与x轴的夹角,ζa表示波幅。 可以看到,KVLCC2在短波范围内的增阻值随波长基本变化不大,不计入辐射增阻的CFD方法计算值以及Faltinsen渐进公式的计算值都同实验值吻合的非常好,也说明了本文数值模拟方法预报船舶在短波中的波浪增阻相当有效。 图11 Fn=0.142时KVLCC2在波浪上增阻的构成Fig.11 Added resistance components of KVLCC2 in head waves, Fn=0.142 图12 Fn=0.142时KVLCC2在短波中的增阻Fig.12 Added resistance coefficient of KVLCC2 in head short waves, Fn=0.142 1)结合重叠网格技术的CFD方法能够准确处理船舶在波浪上的运动响应,相较于势流理论, CFD方法能够在全波长范围内更准确地预报船舶在波浪上增阻; 2)船体遭遇短波时,船体辐射运动非常小,可以忽略,随着波长增加,垂荡幅值和纵摇幅值都迅速增大,船体在长波中航行时无因次的运动幅值趋于1;遭遇足够长的入射波,船体垂荡与波浪同步,相位差0°,纵摇运动相位则落后波浪四分之一周期,船体处于“随浪逐流”状态; 3)Lpp/λ=0.9左右时波浪增阻达到峰值;在短波中船体在波浪中的运动响应比较小,波浪增阻主要由绕射增阻贡献,辐射增阻可以忽略不计;长波范围,船体辐射运动引起的增阻随波浪增大逐渐减小;船舶在波浪中的增阻主要由压力场的改变引起,摩擦对增阻的贡献非常小。 [1] 缪国平, 刘应中. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1989. [2] CARRICA P M, WILSON R V, NOACK R W, et al. Ship motions using single-phase level set with dynamic overset grids[J]. Computers & fluids, 2007, 36(9): 1415-1433. [3] CARRICA P M, WILSON R V, STERN F. Unsteady RANS simulation of the ship forward speed diffraction problem [J]. Computers & fluids, 2006, 35(6): 545-570. [4] GUO B, STEEN S. Evaluation of added resistance of kvlcc2 in short waves [J]. Journal of hydrodynamics, Ser B, 2011, 23(6): 709-722. [5] GUO B J, STEEN S, DENG G B. Seakeeping prediction of KVLCC2 in head waves with RANS [J]. Applied ocean research, 2012, 35: 56-67. [6] SADAT-HOSSEINI H, WU P, CARRICA P M, et al. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves[J]. Ocean engineering, 2013, 59: 240-273. [7] 方昭昭, 赵丙乾, 朱仁传. 顶浪中船舶运动的数值模拟与波浪增阻计算[J]. 中国造船, 2014, 55(2): 8-17. FANG Zhaozhao, ZHAO Bingqian, ZHU Renchuan. Numerical simulation of ship motion and calculation of added resistance in heading waves [J]. Shipbuilding of China, 2014, 55(2): 8-17. [8] 方昭昭, 朱仁传, 缪国平, 等. 基于数值波浪水池的波浪中船舶水动力计算[J]. 水动力学研究与进展A辑, 2012, 27(5): 515-524. FANG Zhaozhao, ZHU Renchuan, MOU Guoping, et al. Numerical calculation of hydrodynamic forces for a ship in regular waves based on numerical wave tank[J]. Journal of hydrodynamics, 2012, 27(5): 515-524. [9] 方昭昭, 朱仁传, 缪国平, 等. 数值波浪水池中航行船舶绕射问题的数值模拟[J]. 上海交通大学学报, 2012, 46(8): 1203-1209. FANG Zhaozhao, ZHU Renchuan, MOU Guoping, et al. Numerical simulation of diffraction problems of moving vessels in numerical wave tank[J]. Journey of Shanghai JiaoTong University, 2012, 46(8): 1203-1209. [10] OURNÉE J M J. Experiments and calculations on 4 Wigley hull forms in head waves[J]. Delft University of Technology, 1992: 909. [11] YE H, SHEN Z, WAN D. Numerical prediction of added resistance and vertical ship motions in regular head waves [J]. Journal of marine science and application, 2012, 11(4): 410-416. [12] 沈志荣, 叶海轩, 万德成. 船舶在迎浪中运动响应和波浪增阻的RANS数值模拟[J]. 水动力学研究与进展A辑, 2012, 27(6): 621-633. SHEN Zhirong, YE Haixuan, WAN Decheng. Motion response and added resistance of ship in head waves based on RANS simulations[J]. Journal of hydrodynamics, 2012, 27(6): 621-633. [13] 齐鹏, 王永学. 三维数值波浪水池技术与应用[J]. 大连理工大学学报, 2003,43(6): 825-830. QI Peng, WANG Yongxue. 3-D numerical-wave-tank technology and its application [J]. Journey of Dalian University of Technology, 2003, 43(6): 825-830. [14] FALTINSEN O M, MINSAAS K J, LIAPIS N, et al. Prediction of resistance and propulsion of a ship in a seaway[C]∥Proceeding of 13th Symposium on Naval Hydrodynamics, Tokyo, Japan, 1980. [15] LARSSON L, STERN F, VISONNEAU M. Numerical ship hydrodynamics [C]//A Workshop on Numerical Ship Hydrodynamics. Gothenburg, Sweden, 2010. 本文引用格式: 曹阳, 朱仁传, 蒋银, 等. 波浪中KVLCC2运动与阻力增加的CFD计算及分析[J]. 哈尔滨工程大学学报, 2017, 38(12): 1828-1835. CAO Yang, ZHU Renchuan, JIANG Yin, et al. CFD verification and analysis of added resistance and motions of KVLCC2 in head waves[J]. Journal of Harbin Engineering University, 2017, 38(12): 1828-1835.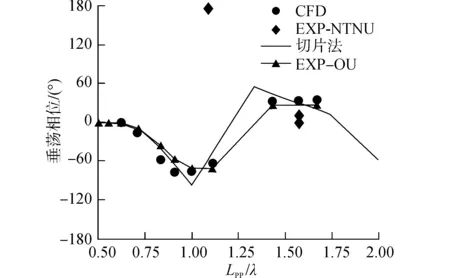
3.2 KVLCC2在波浪中的增阻


3.3 KVLCC2在短波中的增阻
4 结论

