非线性不等式约束优化问题的指数型精确罚函数算法
杨 莲, 姚奕荣
非线性优化问题广泛存在于工程设计、经济管理、军事科研等应用领域.许多学者开始把一些成熟的、有效的算法拓展到求解非线性优化问题中,其中罚函数算法较为引人注目.罚函数算法是求解约束优化问题的一类重要方法,也是一类比较有效的方法.
罚函数算法的基本思想是借助罚函数把约束问题转化为无约束问题,进而利用无约束最优化方法来求解约束问题.Courant[1]首先提出外点罚函数算法,有效地将带有约束的非线性优化问题转化为无约束优化问题.针对非线性不等式约束优化问题,Carroll等[2]提出了内点罚函数算法.精确罚函数的概念由Eremin[3]和Zangwill[4]在20世纪60年代末分别提出.精确罚函数包括非光滑精确罚函数[5-6]和光滑精确罚函数[7].1967年,Zangwill[4]对凸优化问题提出了l1精确罚函数.自此,精确罚函数算法成为解决非线性优化问题的重要方法,人们对该算法开展了许多研究.Rosenberg[8]和Lasserre[9]分别研究了一个精确罚函数算法的全局收敛性.Pinar等[10]提出了一个一次连续可微的罚函数.K¨omer[11]研究了二次规划问题的精确罚函数的数值算法.文献[12]给出了精确罚函数的一个充要条件.在文献[13]中,对于单值标量约束优化问题,Lucidi提出并证明了低阶精确罚函数与原约束优化问题的等价性.对于变分不等式的约束优化问题,文献[14]通过正则间隙函数提出了一个新的精确罚函数.对含有目标约束的优化问题,文献[15]研究了罚函数的精确性并提出了相应的算法.由于表达式中含有目标函数或约束函数的梯度,在实际计算工作中会显得过于复杂,大大制约了这类可微精确罚函数算法的实际应用.因此,非线性精确罚函数算法和低阶罚函数算法得到了广泛的关注,在许多新领域不断有研究成果出现.针对箱子约束的等式优化问题,文献[16]通过增加一个变量,给出了一个新的精确罚函数.
受文献[16]的启发,本工作主要通过增加一个变量,针对非线性不等式约束优化问题构造了一个新的指数型光滑精确罚函数,并证明了该罚函数在集合{(x,ε)|ε=0,x∈S或0<ε<ε}上具有二次连续可微性和精确性质.最后,基于牛顿法设计了一种新的指数型精确罚函数算法,并通过数值计算验证了算法的可行性.
1 指数型光滑精确罚函数
1.1 罚函数的构造
考虑非线性不等式的约束优化问题:
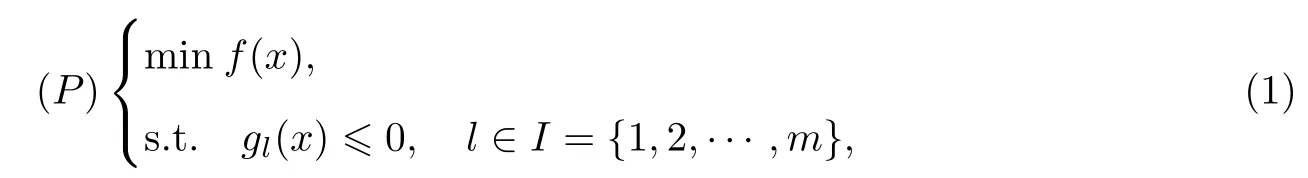
式中,函数f,gl:Rn→R是二次连续可微函数.另记S={x∈Rn:gl(x)≤0,l∈I}.
通过增加一个变量ε,问题(P)等价于
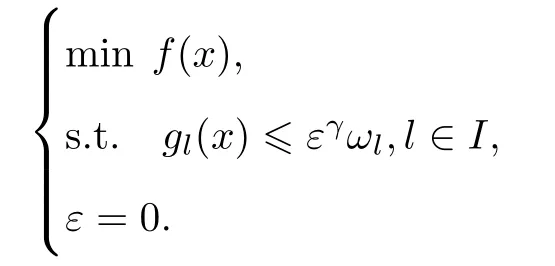
式中,ωl∈ R+为给定的实数.另记 Sε={(x,ε):gl(x)≤ εγωl,l∈ I}.构造相应的罚函数
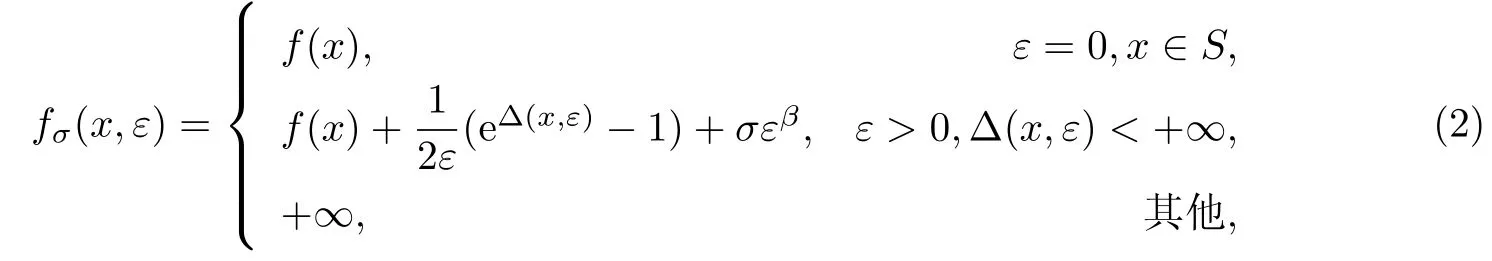
考虑问题(P)的罚问题
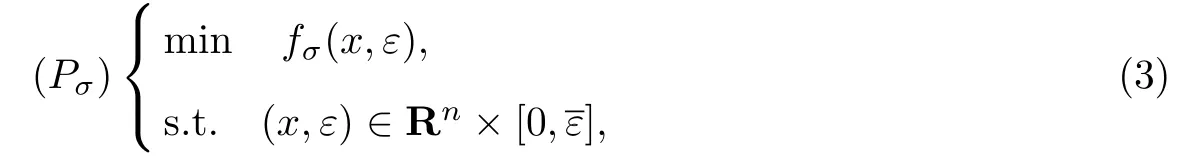
式中,ε>0是一固定的实数.显然,问题(Pσ)是一个无约束优化问题.事实上,当罚参数足够大时,问题(Pσ)的任何局部极小点都是问题(P)的局部极小点.下面对问题(P)做出一些假设:(1)f(x)在可行域S上是下有界的,其中S是一个紧集或是一个无界闭集;(2)x∗∈L(P)是孤立的点,L(P)的数量是有限的,其中L(P)表示问题(P)的局部极小点的集合.
若x∈/S且 ε>0,Δ(x,ε)<+∞,fσ(x,ε)=f(x)+(eΔ(x,ε)− 1)+ σεβ> f(x),则当 Sn是一个无界闭集合且f(x)在S上是下有界时,显然fσ(x,ε)在集合{(x,ε)∈R×[0,ε]:ε =0,x∈S或者ε>0,Δ(x,ε)<+∞}中是下有界的.当S是一个紧集,则对于ε> 0,fσ(x,ε)在集合{(x,ε)∈Rn×[0,ε]:ε=0,x∈S或者ε>0,Δ(x,ε)<+∞}上是下有界的.因此,fσ(x,ε)在集合 Rn× [0,ε]上是有下界的,这表明 fσ(x,ε)在 Rn×[0,ε]上存在局部极小值.
1.2 罚函数的光滑性
设{σk}是一递增的罚参数序列,σk→+∞.对固定罚参数σk,记对应的罚问题(Pσk)的最优解为(xk,εk).为了证明罚函数的光滑性和精确性,作如下假设.
(1)函数f,gl,l=1,2,···,m在Rn上是二次连续可微的.
(2)M-F约束品性在x∗处成立,即如果存在h∈Rn使得对所有的j∈J(x∗),有∇gi(x∗)Th<0,其中J(x∗)={j∈ I|gj(x∗)=0},x∗是问题(P)的局部极小点.
(3)max{0,gl(x(k))}=o((ε(k))σ),σ > 1,l=1,2,···,m.
定理1 若(xk,εk)满足假设(1)∼(3),γ,β,N 满足2N+γ−3>0,N−2>0,Nγ−3>0,β − 2> 0,则当 (x,ε)∈ {(x,ε)∈ Rn×[0,ε]:ε> 0,Δ(x,ε)< +∞},且 ε→ 0,x→ x∗∈ S时,有

成立,其中
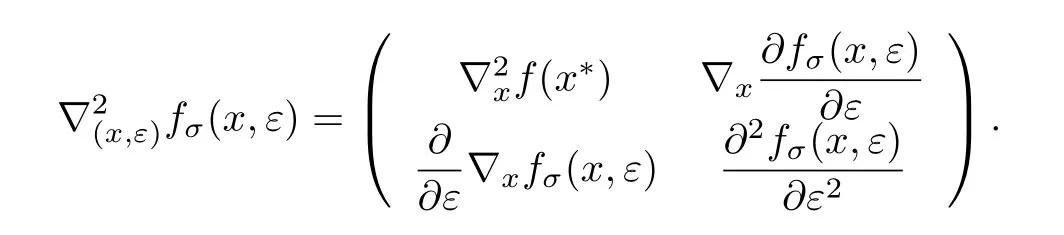
证明 (1)当 ε=0 时,由 fσ(x,ε)的定义可知 fσ(x,ε)=f(x).因此,
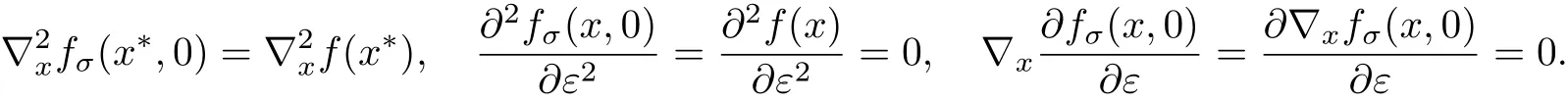
(2)当 ε/=0,(x,ε)∈ {(x,ε)∈ Rn×[0,ε]:ε> 0,Δ(x,ε)< +∞},由 fσ(x,ε)的定义可知
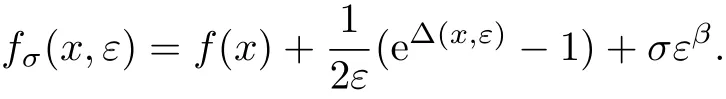
因此,有
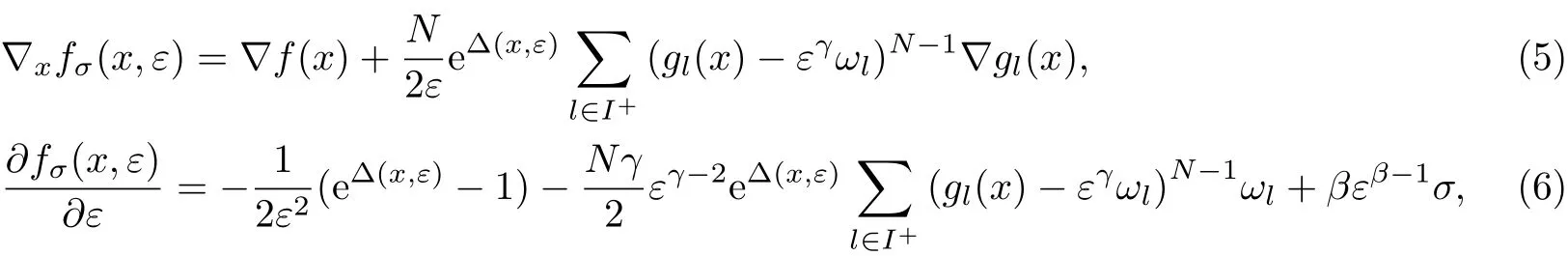

由式(9)和(10)可得,

下面证明当ε→0,x→x∗∈S时,
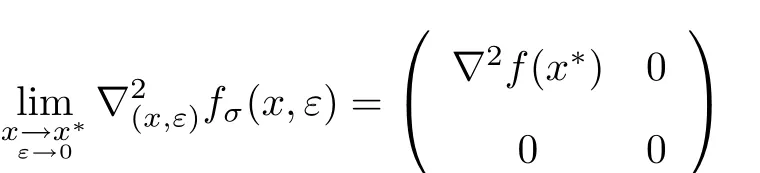
成立.
当ε/=0,ε→0,x→x∗∈S时,由假设(3)可得
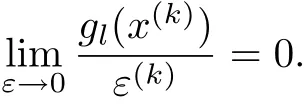
由式(7),(8),(9)和(10)可知,若令γ,β,N 分别满足
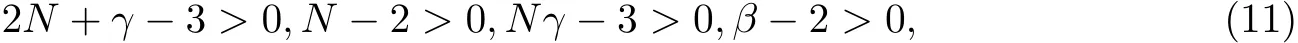
则有
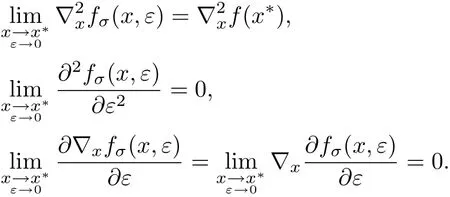
因此,有
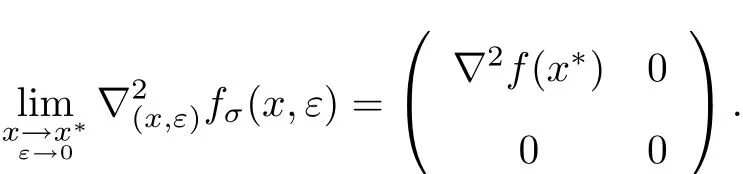
定理得证.定理1表明本工作构造的罚函数是二次连续可微函数.
1.3 罚函数的精确性
下面证明罚问题(Pσ)的局部极小点序列(xk,εk)将会收敛到问题(P)的局部极小点.
引理1 令(xk,εk)是问题(Pσk)的一个局部极小点,且函数值fσk(xk,εk)有限,εk>0.则(xk,εk)/∈Sε={(x,ε):gl(x)≤εγωl,l∈I}.
证明 若 (xk,εk)∈ Sε,由于 (xk,εk)是罚问题 (Pσk)的一个局部极小点且函数值fσk(xk,εk)为有限值,εk> 0,从而有
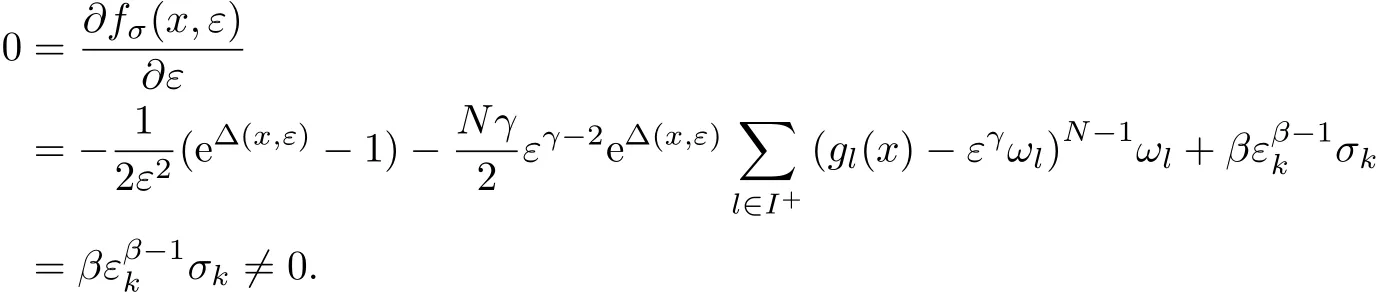
显然,上式矛盾.因此有(xk,εk)/∈Sε.
定理2 设(xk,εk)是罚问题(Pσk)的局部极小点,函数值fσk(xk,εk)有限,εk>0.如果k → +∞,(xk,εk)→ (x∗,ε∗)满足假设条件(1)∼ (3),那么有 ε∗=0,x∗∈ S.
证明由引理1可知,(xk,εk)/∈Sε,于是有∇(x,ε)fσk(xk,εk)=0.因此,有
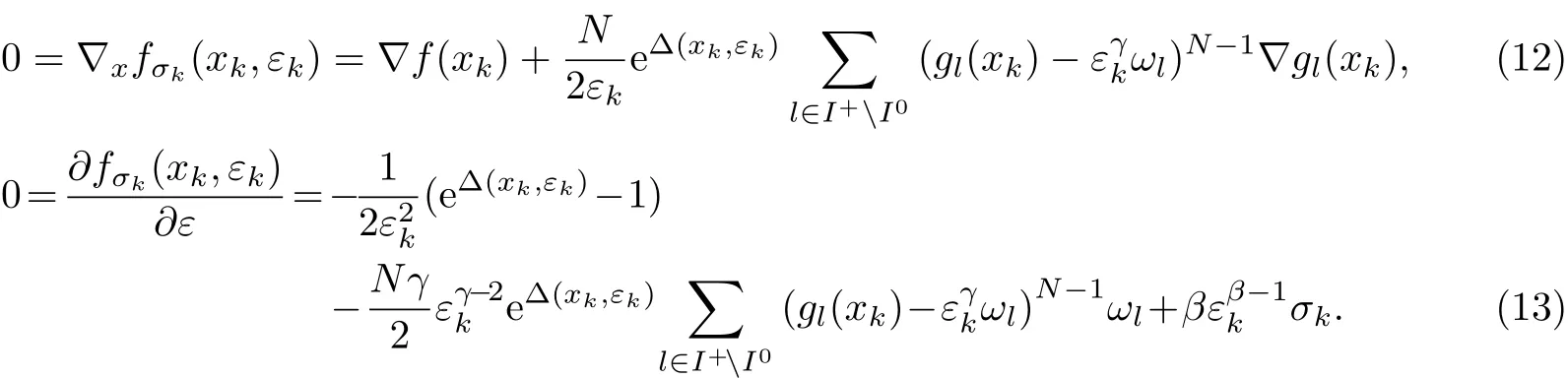
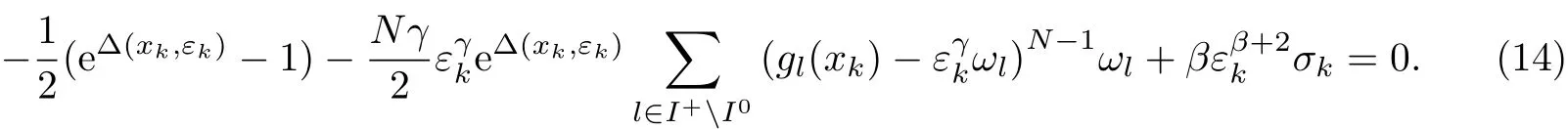
如果ε∗/=0,则当σk→+∞,εk→ε∗,xk→x∗时,式(14)的第一项和第二项均为有限值,第三项则趋于无穷大,等式不可能成立,因此,εk→ε∗=0.此外,由式(12)可知,当εk>0时,
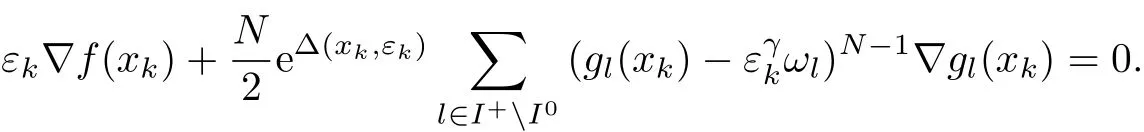
当σk→+∞,εk→ε∗=0时,可以得到
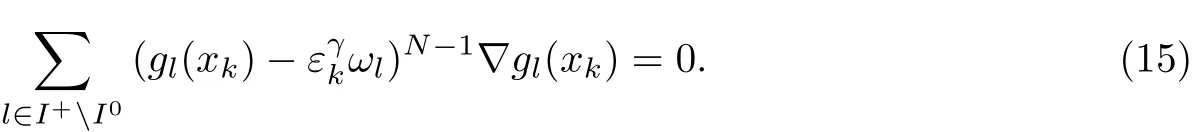
下面证明I+=I0.假设I+/=I0,则存在l0∈I+I0,使得gl0(x∗)>0.由于在x∗处满足假设条件(2),因此存在p∈Rn,p/=0,使得∇Tgl0(x∗)p<0,l0∈I+I0,由此可得
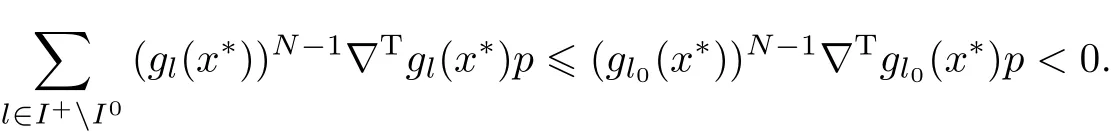
显然上式与式(15)矛盾.因此,I+=I0,且x∗∈S.
引理1和定理2表明局部极小点的序列{(xk,εk)}将收敛到问题(P)的可行解且具有有限的目标函数值,且这个可行解是问题(P)的局部极小点.
下面证明所构造的罚函数fσ(x,e)是精确的.
定理3 假设定理2和条件(式(11))成立,则存在k0>0,使得对任意的k≥k0>0,都有εk→0,xk∈L(P)成立.
证明 假设结论不成立,则存在序列{(xk,εk)}的子序列{(xnk,εnk)},使得对任何k0>0,都存在k′>k0,且满足εk/=0.根据定理2,有
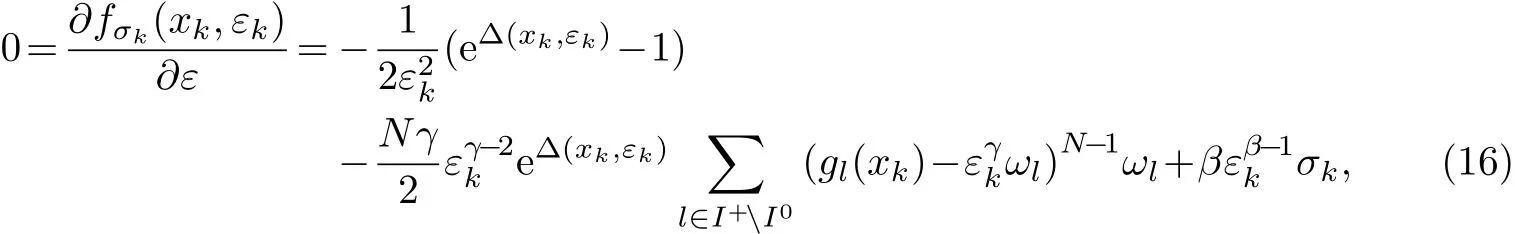
简化上式,可得
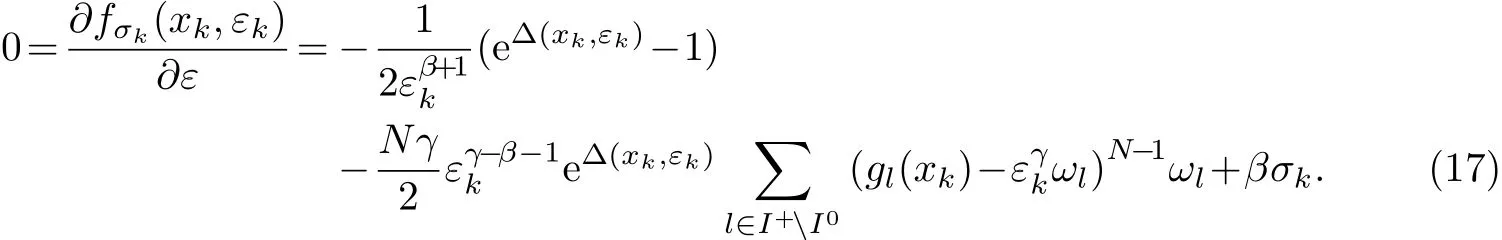
当k→+∞,由定理2可知,εk→ε∗=0,xk→x∗∈S.因为式(17)的第一项和第二项为有限值,而式(17)的第三项趋于∞,所以式(17)矛盾,因此子序列{(xnk,εnk)}不存在.故定理为真.
定理1和定理3表明所构造的罚函数是光滑的和精确的.
2 罚函数算法及数值计算
2.1 罚函数算法
第1步 选择适当的(x0,ε0)∈Rn×[0,ε],ε>0使得Δ(x0,ε0)>0,σ0>1足够大,δ>0足够小,H0是一正定矩阵.令k:=0.
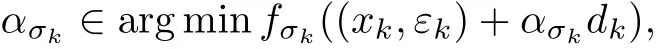
Hk是一正定矩阵.再令ασk满足
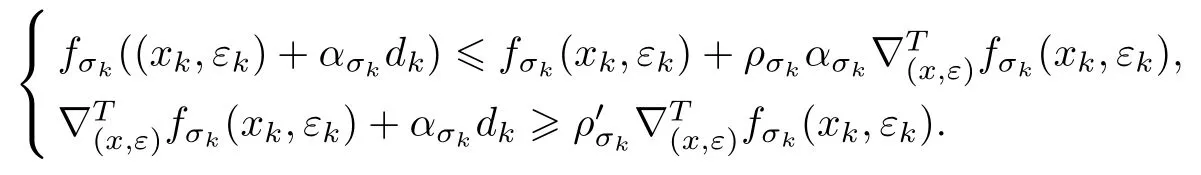
第 4 步 令 (xk+1,εk+1)=(xk,εk)+ασkdk,σk+1=cσk,其中c>1 为常数.
第5步 令k:=k+1,返回第2步.
2.2 数值计算
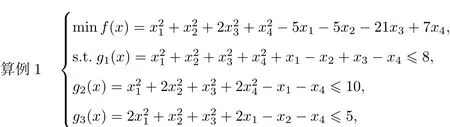
此问题的最优解和最优值分别为=(0,1,2,−1)和f(x∗)=−44.在本算例中,取x0=(0.5,1.5,1.5,−1.5),ε0=2.0,N=8,α=6,β=4,ω=0.05.运用Matlab 7.11软件计算,结果如表1所示.

表1 算例1的数值计算结果Table 1 Numberical calculation results of Example 1
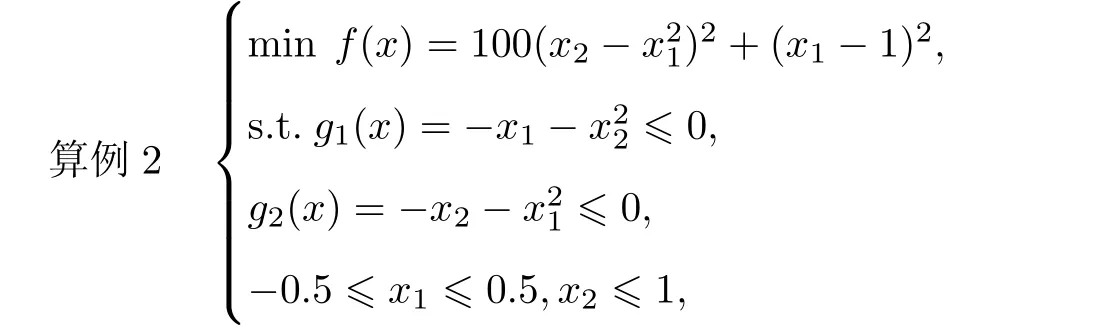
此问题的最优解和最优值分别为x∗=(0.50,0.25)和f(x∗)=0.25.在本算例中,取x0=(−1,0),ε0=1.0,N=4,α=4,β=4,ω=0.05.运用Matlab 7.11软件计算,结果如表2所示.

表2 算例2的数值计算结果Table 2 Numberical calculation results of Example 2
算例1和算例2表明,通过选择合适的参数可以得到原问题的近似最优解,从而说明所设计的罚函数算法是可行的.
3 结束语
本工作针对非线性不等式约束优化问题,通过加入一个变量构造了一种新的指数型光滑精确罚函数,并对罚函数的光滑性和精确性进行了讨论.另外,还设计了求解原问题的精确罚函数算法.对于大规模的优化问题,如何提出一种更好的算法,需要进一步的研究和讨论.
[1]COURANT R.Variational methods for the solution of problems of equilibrium and vibrations[J].Bulletin of the American Mathematical Society,1943,49:1-23.
[2]CARROLL C W,FIACCO A V.The created response surface technique for optimizing nonlinear restrained systems[J].Operations Research,1961,9(2):169-184.
[3]EREMIN I I.The penalty method in convex programming[J].Cybernetics and Systems Analysis,1967,3(4):53-56.
[4]ZANGWILL W I.Nonlinear programming via penalty function[J].Management Science,1967,13(5):344-358.
[5]ANTCZAk T.Exact penalty function method for mathematical programming problem involving invex function[J].European Journal of Operational Research,2009,198(1):29-36.
[6]ZASLAVSkI A J.Existence of exact penalty for constrained optimization problems in Metric spaces[J].Set-Valued Analysis,2007,15(3):223-237.
[7]ZHENG F Y,ZHANG L S.New simple exact penalty function for constrained minimization[J].Applied Mathematics and Mechanics(English Edition),2012,33(7):951-962.
[8]ROSEBERG E.Globally convergent algorithms for convex programming with applications to geometric programming[J].Mathematics of Operations Research,1981,6(3):437-443.
[9]LASSERRE J B.A globally convergent algorithm for exact penalty functions[J].European Journal of Operational,1981,7(4):389-395.
[10]PINAR M C,ZENIOS S A.On smoothing exact penalty functions for convex constrained optimization[J].SIAM Journal on Optimization,1994,4(3):486-511.
[11]K¨OMER F.On the numerical realization of the exact penalty method for quadratic programming algorithm[J].European Journal of Operational Research,1990,46(3):404-409.
[12]张连生.全局精确罚函数的一个充要条件[J].数学年刊(A辑),1997,18(5):579-586.
[13]LUCIDI S.New results on a continuously diあerentiable exact penalty function[J].SIAM Journal on Optimization,1992,2(4):558-574.
[14]LI W,PENG J.Exact penalty functions for constrained minimization problems via regularized gap function for variational inequalities[J].Journal of Global Optimization,2007,37(1):85-94.
[15]MENG Z Q,DANG C Y,JIANG M,et al.Exactness and algorithm of an objective penalty function[J].Journal of Global Optimization,2013,56(2):691-711.
[16]HUYER W,NEUMAIER A.A new exact penalty function[J].SIAM Journal on Optimization,2003,13(4):1141-1158.

