采用伪噪声重采样的海事卫星上行信号的检测与定向
王佳栋 王晓江, 牛丽莹, 郑国莘
信号来波方向估计在雷达、地面无线通信以及卫星通信中具有广泛的应用.对国际海事卫星(Inmarsat)终端移动设备发出的上行信号的准确检测与定位,在军事上能够精确地掌握敌方行动,在民用上则能对求救者提供及时的帮助[1].
信号接收端的天线阵列以其高增益、强抗干扰能力以及高分辨率为方向角估计提供准确的数据.Roy等[2]提出的ESPRIT算法和Schmidt[3]提出的MUSIC算法是波达方向(direction of arrival,DOA)估计系统中最早提出的两种方法.Huarng等[4]提出一种应用于MUSIC算法的酉变换,减小了计算的复杂度.但是经典的MUSIC算法以及ROOT-MUSIC算法均受限于系统信噪比(signal noise ration,SNR).基于此,Gershman[5]提出了一种基于统计学的联合估计策略,提高了阵列在低信噪比下的分辨率.之后Gershman等[6]在进行谱峰搜索时引入伪随机加权因子,提出了空间谱的伪随机重采样(pseudo-noise resampling,PR).在Zoubir等[7]工作的启发下,Gershman等[8-9]在接收阵列上适当加入噪声并进行重组,极大地排除了系统接收矩阵的异常值,之后,Gershman等[10]又将伪噪声重采样应用于波束空间ESPRIT算法.Vasylyshyn[11]基于传统的波束形成将伪噪声重采样与ROOT-MUSIC算法相结合,给出了传统先验条件的假设方法.另外,Vasylyshyn[12]还利用重采样技术提升了ESPRIT算法精确度.Qian等[13]针对伪噪声重采样系统在所有重采样估计结果均不符合先验条件的情况下,通过改进传统的均值与中值方法并结合距离检测策略(distance detection strategy,DDS)进行估计,提升了低信噪比下的分辨率.上述研究均基于线性阵列(uniform linear array,ULA),但ULA只能提供180°方位角估计.均匀圆形阵列(uniform circular array,UCA)可以提供360°无模糊的全方位角估计,因此在现代通信中作用更广.Ma等[14]利用模式空间算法将UCA转换成虚拟ULA,使得基于ULA的算法可以应用于UCA.Zoltowski等[15]则将常规ROOT-MUSIC算法应用于UCA.
结合文献[10]中的方法,本工作提出一个应用于UCA的伪噪声重采样酉ROOT-MUSIC算法,提高了UCA系统在低信噪比下DOA估计精度.传统伪噪声重采样先验条件要求信噪比较高,即波束形成输出存在一个明显的峰值,且峰值两边应存在3 dB衰落的区间.但当信噪比较低时,UCA系统的波束形成存在多个谱峰值,且峰值两边衰落小于3 dB.针对上述情况,本工作利用噪声的高斯特性,采取多次估计的均值以及标准差形成新的先验条件,使得伪噪声重采样在低信噪比下也可以应用于UCA.
1 相位模式激励
UCA模型如图1所示,其中m个天线阵子均匀分布在圆周上,接收p个不同来波方向的信号.
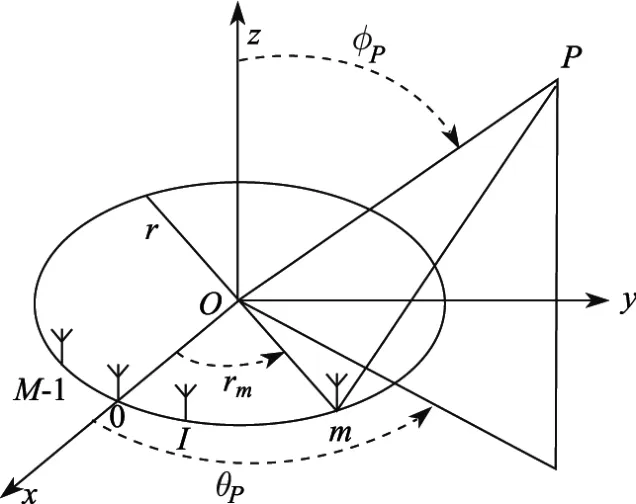
图1 UCA模型Fig.1 UCA model
根据图1,阵列接收矩阵可表示为

式中: 方向矢量 A=[a(θ1,φ1),a(θ2,φ2),···,a(θP,φP)],其中

方向角θi∈[0,2π]为x轴沿逆时针方向得到的投影夹角;为z轴与信源的夹角,r为阵列半径,λ为信号波长;rm=2πm/M,为第m个阵元与圆心之间的连线与x轴的夹角,0≤m<M.由于工程中手机分布在二维平面,这里φi固定为90°.
由式(2)可知,UCA阵元方向矢量不具有范德蒙德结构.根据文献[14]中提出的相位模式激励,利用下式进行虚拟ULA转换:

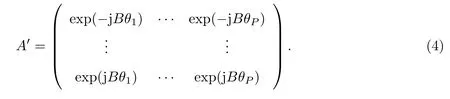
显然,A′具有范德蒙德结构形式.
2 伪噪声重采样
2.1 伪噪声重采样
由于噪声的随机性,估计量表现出随机性的特点.基于此,伪噪声重采样对接收矩阵进行多次伪噪声的叠加,打乱接收矩阵,扩大噪声的方差,将原先不成功的估计有可能落在成功的区域[8,10].估计量分为两种,成功的估计可以成功分解信号,不成功的估计值即为异常值.伪噪声重采样的目的就是将异常值尽可能地消除.
针对每一次计算,需要一个假设条件C(本次ROOT-MUSIC结果得到的P个来波方向均满足先验条件^Θ)对两种估计量进行区分.当ROOT-MUSIC结果满足条件C时,估计值可以直接作为本次估计的结果;而当结果不满足条件C时,则需要进行伪噪声重采样.先验条件^Θ是一种通过波束成形对信号源位置的预估计范围,表示为
例如2016年广东省中考题第14题,已知了电阻甲和乙的IU,可以得出电阻乙的阻值为6Ω,若把电阻甲和乙并联后接在电压为6V电源两端时,则干路的总电阻为多少?总功率为多少?
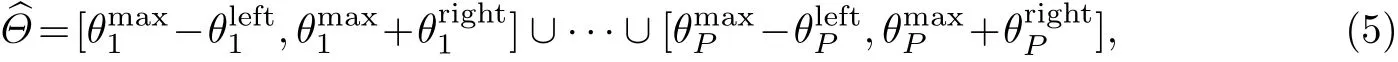
下面根据文献[11]中的方法求得波束成形结果,首先对来波方向进行n次常规ROOTMUSIC计算,得到p个角度信息以及相应的计算根.
第1步 将第i次(0<i≤n)估计的角度信息组成集合θi以及对应的根集合Z,则
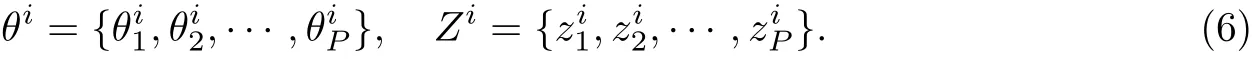
第2步 对接收矩阵X进行K次重采样计算,施加的伪噪声Y∼N(0,ρ·),其中为原系统噪声的方差,ρ为伪噪声系数.针对第p个信号源,重采样后ROOT-MUSIC计算结果的集合为

第3步 判定Aθ,p中是否有(0<k≤K)符合条件C.若有J(0<J≤K)次符合,则组成新的Aθ,p与Az,p:
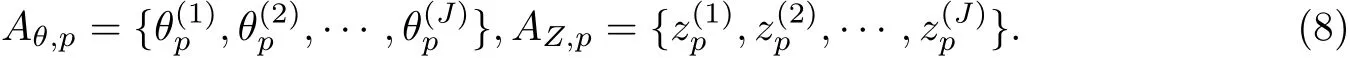
然后将Aθ,p中的J次结果作为本次重采样的成功集合,根据

计算第i次DOA结果.若J=0,则说明第i次DOA估计中重采样没有将异常值移除,接下来利用直接数字式频率合成器(direct digital synthesizer,DDS)决定,并重复第1步至第3步n次,再跳转至下一步.
第4步 根据

计算第p个信号源估计结果.
3 低信噪比下的先验条件
伪噪声重采样要求阵列波束形成输出中能够找到目标峰值,且峰值两边衰落达到3 dB.但是,低信噪比下UCA往往不满足这个条件.图2为一个低信噪比下的UCA波束形成输出[1],其中信号频率为1.6 GHz,采样率为1 Gbits,信号源方向θ=60°,φ=90°,阵元数m=16,阵列半径r=λ,每个天线接收到的信号信噪比均为−10 dB.由图2可以看出,峰值2(实际来波)两边的衰落小于3 dB,3(来波干扰)的峰值最高,产生误判.

图2 低信噪比下的UCA波束形成输出Fig.2 Beamformer output of UCA at low SNR
由于低信噪比下采用波束形成法无法得到原先验条件^Θ,因此伪噪声重采样无法进行.基于此,本工作提出如下方法进行先验条件的假设,以此取代波束形成,使伪噪声重采样可以在低信噪比下应用于UCA.

式中:为第p个阵元的第i次角度估计(未经重采样),α为先验系数,α越大表示预估范围越大.由于噪声的原因,单次估计时可能会出现较大的偏差,但经过足够多的实验可得到估计的角度集.根据噪声的特性,角度集的平均值接近实际来波方向.因此,根据式(11)可以求得和,然后将其代入式(5)中得到新的先验条件.在此基础上,再按式(6)∼(10)进行重采样.当预估范围较小时,系统会将原先在成功区域的估计判定为异常值,噪声重复叠加,导致系统性能下降;当预估范围过大时,系统则将异常值判定为成功估计,不进行重采样,导致系统性能无法改善.因此,只有选择合适的α,才能使系统的性能最佳.
4 仿真实验与结果
根据式(11),将重采样技术应用于UCA,比较伪噪声重采样ROOT-MUSIC(PR-ROOTMUSIC)算法与ROOT-MUSIC算法的性能.仍然采用文献[1]中的算例进行仿真.首先构造虚拟ULA,并在ROOT-MUSIC算法不能正常估算信号方向时进行重采样,当重采样不能将异常值排除时则利用DDS策略帮助决定最终的估算值.研究发现,只要选定合适的伪噪声系数与先验系数,就可以使系统估计均方根误差(root mean squared error,RMSE)尽可能小,从而有效地找到实际来波方向.
4.1 伪噪声系数
图3为伪噪声系数不同时信噪比对系统性能的影响,这里重采样次数K=30,实验次数n=1 000,信噪比为−15∼0 dB,采样点数N=100,先验系数α=1.由图3可以看出,在信噪比低于−5 dB的情况下,伪噪声系数ρ越大,系统性能越好.因此,仿真实验时选取伪噪声系数ρ=1.0.

图3伪噪声系数不同时对系统性能的影响Fig.3 Eあects on the system versus diあerent PR coeきcients
4.2 先验系数
图4 为先验系数α不同时信噪比对系统性能的影响,这里K=30,n=1 000,N=100,ρ=1.0.由图4可以看出:当α=2.0,3.0时,系统将异常值误判为正常值,导致重采样概率减小,但系统性能并没有较好的改善;当α<1.0时,系统将正常值误判为异常值,重复施加噪声,系统性能变得更差.综上分析可知,当α=[0.5,1.0]时,系统拥有最佳的性能.因此,在仿真实验中采用α=1.0计算预估边界.
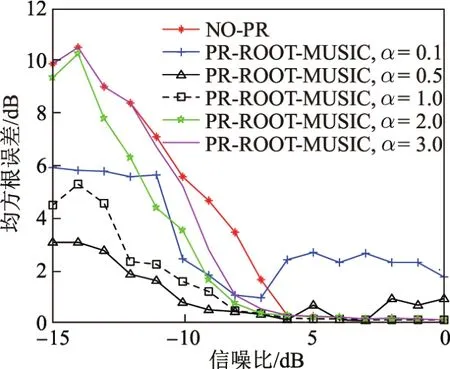
图4先验系数对系统性能的影响Fig.4 Eあects on the system versus diあerent α
4.3 采样点数
图5 为信噪比为−5 dB,n=1 000时采样点数不同对系统性能的影响.由图可以看出,在相同条件下,采样点数越多,系统均方根误差越小.但是当K=5时,重采样次数偏小,不能完全将异常值去除,并且有可能会带入新的噪声,从而可能导致结果更差.
4.4 实验次数
图6为SNR=−5 dB,N=100时实验次数不同对于实验结果的影响,其中黑色曲线为常规ROOT-MUSIC算法结果,红色曲线为酉变换ROOT-MUSIC算法结果,绿色曲线为采用中值策略的重采样结果,蓝色3条曲线分别对应不同K值下的计算结果.整体来看,实验次数越大,系统均方根误差越小.局部来看,当实验次数较小时,实验次数的变化对于系统的影响较大,当实验次数超过500次时,系统性能变化较缓慢.
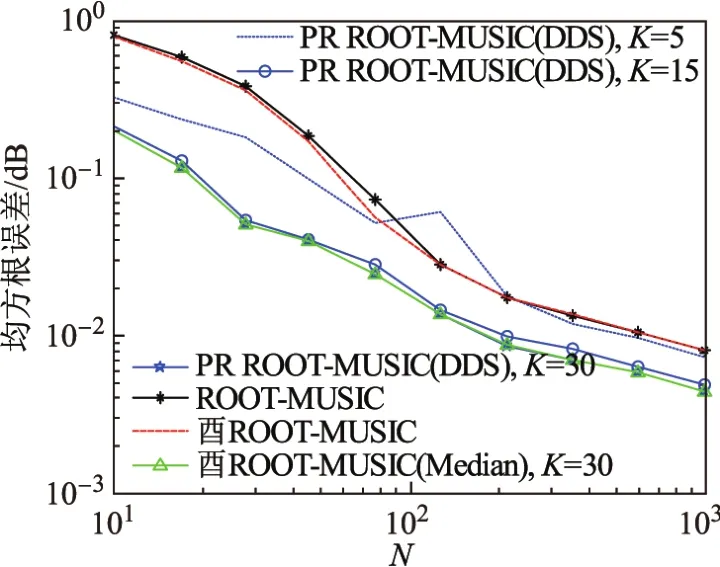
图5 采样点数不同时系统均方根误差的比较Fig.5 RMSE of system versus diあerent samples
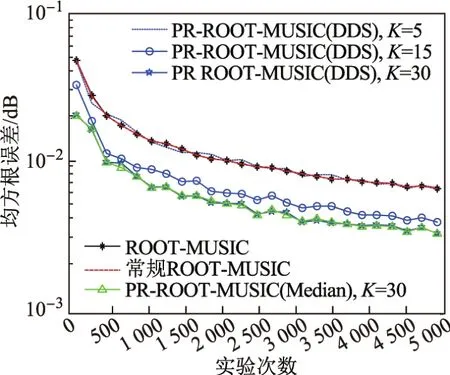
图6 实验次数不同时系统均方根误差的比较Fig.6 RMSE of system versus diあerent number of trials
4.5 与常规ROOT-MUSIC算法的比较
现将本工作提出的PR-ROOT-MUSIC算法与文献[15]中的常规ROOT-MUSIC算法进行比较,结果如图7所示,这里ρ=1.0,α=1.0,N=500,n=1 000.由图7可以看出:在信噪比小于−5 dB时,PR-ROOT-MUSIC算法比常规ROOT-MUSIC算法性能有所提升,并且信噪比越小,二者性能差距越大;在系统均方根误差均为1时,PR ROOT-MUSIC所需信噪比可以比常规ROOT-MUSIC算法降低4 dB;当重采样次数K越大,系统的性能更好的提升;随着信噪比的提升,PR-ROOT-MUSIC算法与常规ROOT-MUSIC算法的性能差距逐渐减小,当信噪比超过−5 dB时,二者均方根误差基本相同.

图7 PR ROOT-MUSIC算法与常规ROOT-MUSIC算法的比较Fig.7 Comparition of system performance between PR-ROOT-MUSIC and unitary ROOT-MUSIC
5 卫星电话实测与测量误差预测
本工作实际测试了海事卫星电话IsatPhone上行信号的强度.接收端利用Agilent N9912A进行数据采集,参数如表1所示.

表1 测试系统参数Table 1 Parameters of test system
由于当收发距离超过700 m时,信号已淹没于噪声.因此,实验选取d=1,10,50,100,200,300,400,500,600,700 m处进行测量.图8比较了理论上的大尺度损耗公式与实验测试结果之间的接收功率.由图8可以看出,随着距离的增加,两条曲线基本重合.
自由空间大尺度公式为
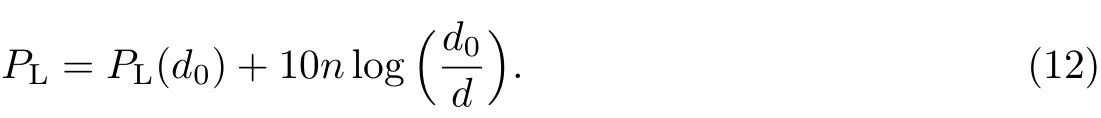
将实验数据代入式(12),得到参数d0=10 m,n=2.1,PL(d0)=−39.08 dBm.
根据图8可以预测不同收发距离下到达角的测量误差.根据式(12)以及图7中的PRROOT-MUSIC(DDS),K=30曲线,将提出的方法应用于实际工程中,在无遮挡物以及单接收天线的前提下,得到图9所示的结果.图中曲线显示了在实际中距离与测量均方根误差之间的关系,可以看出即使在3.5 km的距离下,角度的均方根误差依然在1°以下.

图8 收发距离不同时上行信号程度的比较Fig.8 Upstream intensity in test versus standard large-scale path loss

图9 收发距离不同时到达角的测量误差Fig.9 Predicting measurement error of system
6 结束语
本工作将随机噪声重采样应用于均匀圆形阵列系统中,针对低信噪比下已有方法的局限以及海事卫星上行信号的检测需求,利用多次试验得到的实验估计均值与标准差作为先验条件,当结果不满足先验条件时进行重采样,比较了不同的统计数据形成的先验条件对系统性能的影响,得出最佳先验系数为0.5∼1.0.仿真实验证明了在低信噪比下,PR-ROOT-MUSIC算法的性能比常规均匀圆形阵列ROOT-MUSIC有较大提升.仿真在信噪比小于−5 dB时,随着信噪比降低,两种算法性能差距逐渐扩大.在系统均方根误差均为1时,PR-ROOT-MUSIC算法所需信噪比比常规ROOT-MUSIC算法降低4 dB.通过对海事卫星上行信号功率进行了实地测量,拟合大尺度损耗公式,预测系统在角度误差为1°的范围内,检测距离可达3.5 km.
[1]汪志斌.Inmarsat海事卫星系统的应用与发展[J].上海信息化,2010(11):50-52.
[2]ROY R,PAULRAj A,KAILATH T.ESPRIT-a subspace rotation.approach to estimation of parameters of cisoids in noice[C]//IEEE Trans Acoust Speech Signal Proceeding.1986:1340-1342.
[3]SCHMIDT R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280.
[4]HUARNG K C,YEH C C.A unitary transformation method for angle-of-arrival estimation[J].IEEE Transactions on Signal Processing,1991,39(4):975-977.
[5]GERSHMAN A B.High-resolution direction-f i nding using eigendecomposition based estimators and joint estimation strategy[J].Electronics Letters,1991,27(25):2308-2309.
[6]GERSHMAN A B,B¨OHME J F.Improved DOA estimation via pseudorandom resampling of spatial spectrum[J].IEEE Signal Processing Letters,1997,4(2):54-57.
[7]ZOUBIR A M,BOASHASH B.The bootstrap and its application in signal processing[J].IEEE Signal Processing Magazine,1998,15(1):56-76.
[8]GERSHMAN A B,B¨OHMEA J F.A pseudo-noise approach to direction f i nding[J].Signal Processing,1998,71(1):1-13.
[9]GERSHMAN A B.Pseudo-randomly generated estimator banks:a new tool for improving the threshold performance of direction f i nding[J].IEEE Transactions on Signal Processing,1998,46(5):1351-1364.
[10]GERSHMAN A B,HAARDT M.Improving the performance of unitary ESPRIT via pseudo-noise resampling[J].IEEE Transactions on Signal Processing,1999,47(8):2305-2308.
[11]VASYLYSHYN V.Removing the outliers in root-MUSIC via pseudo-noise resampling and conventional beamformer[J].Signal Processing,2013,93(12):3423-3429.
[12]VASYLYSHYN V.Improved beamspace ESPRIT-based DOA estimation via pseudo-noise resampling[C]//IEEE 2012 9th European Radar Conference(EuRAD).2012:238-241.
[13]QIAN C,HUANG L,SO H C.Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J].IEEE Signal Processing Letters,2014,21(2):140-144.
[14]MA C L,PENG Y N,TIAN L S.An improved MODE algorithm for DOA estimation based on UCA[C]//IEEE Region 10 Annual Conference.Speech and Image Technologies for Computing and Telecommunications.1997,2:811-814.
[15]ZOLTOWSkI M D,MATHEWS C P.Direction f i nding with uniform circular arrays via phase mode excitation and beamspace root-MUSIC[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing.1992,5:245-248.

