四足机器人对角小跑步态控制策略分析

雷静桃,贾光辉

四足机器人因非结构化环境适应性强、承载能力高、低能耗等特点,在星际探测、军事、反恐排雷和娱乐等领域具有广阔的应用前景.四足机器人已成为仿生机器人领域的研究热点.美国波士顿动力公司研制的高性能四足仿生机器人Bigdog和Littledog,具有非结构化环境的良好机动性[1].山东大学、哈尔滨工业大学、国防科技大学、上海交通大学、华中科技大学、中国科学院自动化研究所等机构研发的高性能四足仿生机器人,也取得了一系列成果[2-4].

关于四足机器人步行控制算法的研究,很多学者采用基于中枢模式发生器(central pattern generator,CPG)控制算法进行机器人节律运动控制.CPG不需要外部输入作用,而是通过神经元之间的相互抑制实现自激振荡,产生具有稳定相位互锁关系的多路或单路周期信号,控制机器人相应关节节律运动[5].对于四足机器人步态规划,应用较为广泛的神经振荡器为Matsuoka振荡器、Hopf振荡器、Hodgkin-Huxley振荡器和Van Del Pol振荡器等.

美国加利福尼亚大学的Billard采用漏积CPG模型[6]控制机器狗Aibo,其中8个振荡器组成CPG网络,每个振荡器由两个相互抑制的漏极积分神经元组成,控制一个关节.日本九州工学院的松冈清利研究了生物神经细胞的适应现象,对漏极积分器微分方程进行了改进,通过加入模拟神经元疲劳特性的适应项,构成Matsuok神经元振荡器模型[7].该模型简洁、易用,但在阶跃输入时,输出呈单调递增趋势,而实际神经元在脉冲发放过程中具有疲劳、自抑制特性.瑞士洛桑联邦理工学院基于Hopf振荡器研制了一款四足机器人Cheetah[8],该机器人每条腿有3个关节,髓、膝关节由电机驱动,踝关节是被动自由度,由弹簧驱动.与Matsuoka振荡器相比,Hopf振荡器的输出鲁棒性较差.基于生物神经振荡器的结构和动力学行为,Wilson和Cowan提出了一种简单的神经振荡器模型Wilson-Cowan神经振荡器[9],该生物仿生模型包含兴奋和抑制神经元,且两个神经元之间通过相互耦合产生稳定的极限环振荡.山东大学的李彬等[10]在Wilson-Cowan神经振荡器的基础上提出了一种新的CPG控制器,用于四足机器人的节律运动控制,每个Wilson-Cowan神经振荡器分别对应机器人的一个步行腿,对机器人的腿进行协调运动控制.通过调整振荡器之间的步态连接权矩阵,可以实现机器人不同的节律运动和各种运动模式间的转换.该控制方法能够稳定地生成不同步态的机器人运动轨迹,输出结果能够较好地符合各种步态的相位要求.

采用CPG进行四足机器人运动控制具有明显的优点.CPG控制具有自动稳定特性,受到外部干扰情况下,能够较快地恢复到正常工作状态[11].此外,具有模型参数化特性.CPG控制可将神经-本体-环境系统的复杂的动力学和运动学等浓缩在有限的参数内,通过调节参数得以要求的输出特性,而不需要对整个系统进行建模.不足之处在于模型复杂,CPG控制系统的输出结果没有理想的表达[12-13].

本工作开展了基于CPG控制策略的四足机器人对角小跑步态仿真与实验研究.首先,规划了四足机器人对角小跑步态,采用D-H坐标法进行了四足机器人运动学分析,获得了四足机器人关节角位移与足端期望轨迹间的映射关系.设计由兴奋神经元和抑制神经元共同组成的CPG控制器,其中CPG模型产生稳定平滑的节律振荡,在模型中加入反馈相,通过反馈相改变振荡波形,从而改变机器人的运动步态.CPG的输出用以控制四足机器人的髋关节和膝关节.对四足机器人对角小跑步态的仿真与实验研究,为提高四足机器人非结构化环境的机动性奠定基础.

1 四足机器人对角小跑步态

1.1 四足机器人

四足机器人由前机体、后机体、仿生脊柱和4条仿生腿组成,如图1所示.四足机器人的仿生腿由3个主动转动关节和1个被动踝关节组成,其中3个主动关节分别是侧摆髋关节、前后摆髋关节和膝关节.四足机器人的结构尺寸参考小型犬的体形参数,以期达到较好仿生效果,其中大腿和小腿连杆参考动物胫骨、股骨,机体尺寸则借鉴小型犬的尺寸.四足机器人整体结构紧凑,步行时机体重心移动幅度较小,能提高动态步行稳定性.

图1 四足机器人Fig.1 Quadruped robot

1.2 对角小跑步态

四足机器人采用对角小跑步态,一个步态周期可分为摆动相(sw)和支撑相(sp).腿机构空中摆动的时间段Tsw为摆动相,腿机构支撑于地面时间段为支撑相Tsp,且Tsw=Tsp=T/2,T为一个步态周期.处于对角线上的两条腿动作完全一样,即同时处于摆动相或支撑相.对角小跑步态的时序图,如图2所示,其中腿1与腿3为一组,右前腿4与左后腿2为一组.

图2 对角小跑步态时序图Fig.2 Sequence diagram of trot gait

1.3 四足机器人足端轨迹规划

足端轨迹规划即确定足端在空间经过的曲线轨迹,若采用不同的足端轨迹,则四足机器人的动态性能不同.足端轨迹运动序列可分为“抬腿—摆腿—落下”,对于每个运动序列关节函数不同.A→B为摆动相足端轨迹,支撑相时的机体向前移动的轨迹相当于足端B→A的轨迹,如图3所示.

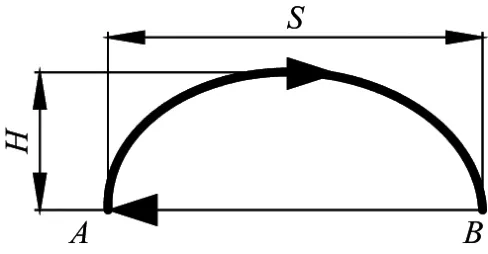
图3 足端轨迹示意图Fig.3 Diagram of foot trajectory planning

若暂不考虑腿机构的侧摆运动,则在足端轨迹侧摆方向上py=0.设定约束条件为

则四足机器人足端轨迹规划为

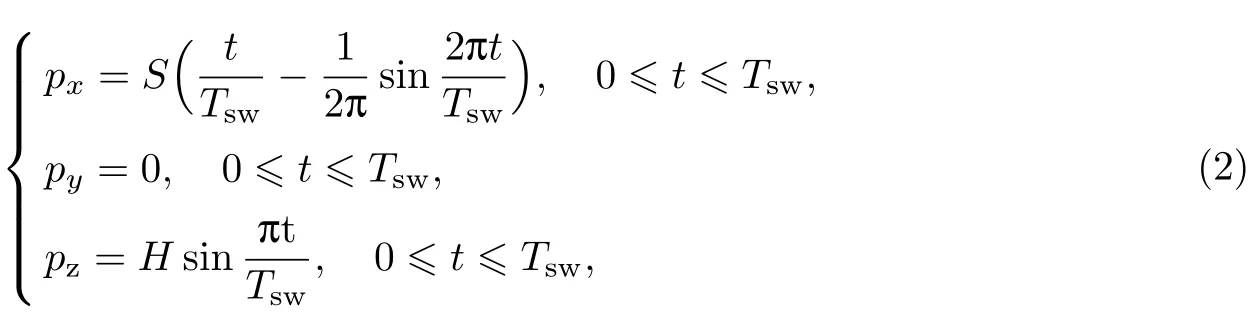
式中:S为步距;H为步高;px,py,pz分别表示足端沿x,y,z方向的位移.当S=100 mm,H=60 mm时,四足机器人一个对角小跑步态周期为10 s,摆动相和支撑相各为5 s.

机器人的腿处于支撑相时,足端的位置相对于固定坐标系是静止不动的,始终保持摆动相终点的状态,此时足端与地面接触,机器人的机体通过腿的运动实现前移.机器人的机体相对于固定坐标系的移动可以转化为足端相对于机体的移动.机体的前移轨迹函数为

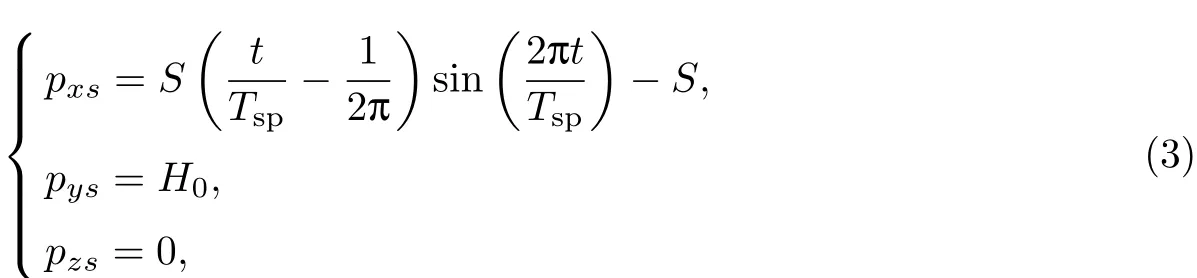
式中:H0为机体高度;pxs,pys,pzs分别表示足端相对于机体沿x,y,z方向的位移.

2 运动学分析

四足机器人腿可看作开式运动链,是由若干连杆通过转动关节串联而成.采用D-H坐标法进行运动学分析,分别获得四足机器人腿处于摆动相和支撑相关节变量与足端期望轨迹间的关系.

2.1 腿处于摆动相

四足机器人腿处于摆动相的运动学模型为[14]

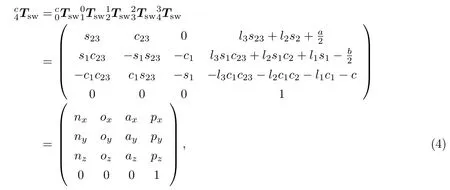
式中:si=sinθi,ci=cosθi,sij=sin(θi+θj),cij=cos(θi+ θj),i=1,2,3,j=1,2,3;l1,l2,l3分别表示侧摆腿、大腿和小腿的长度;a,b,c分别表示机体的长、宽、高;θ1,θ2,θ3为关节变量.

由四足机器人腿机构正运动学模型,采用反变换法进行运动学逆解分析,则腿机构处于摆动相时,各关节变量为

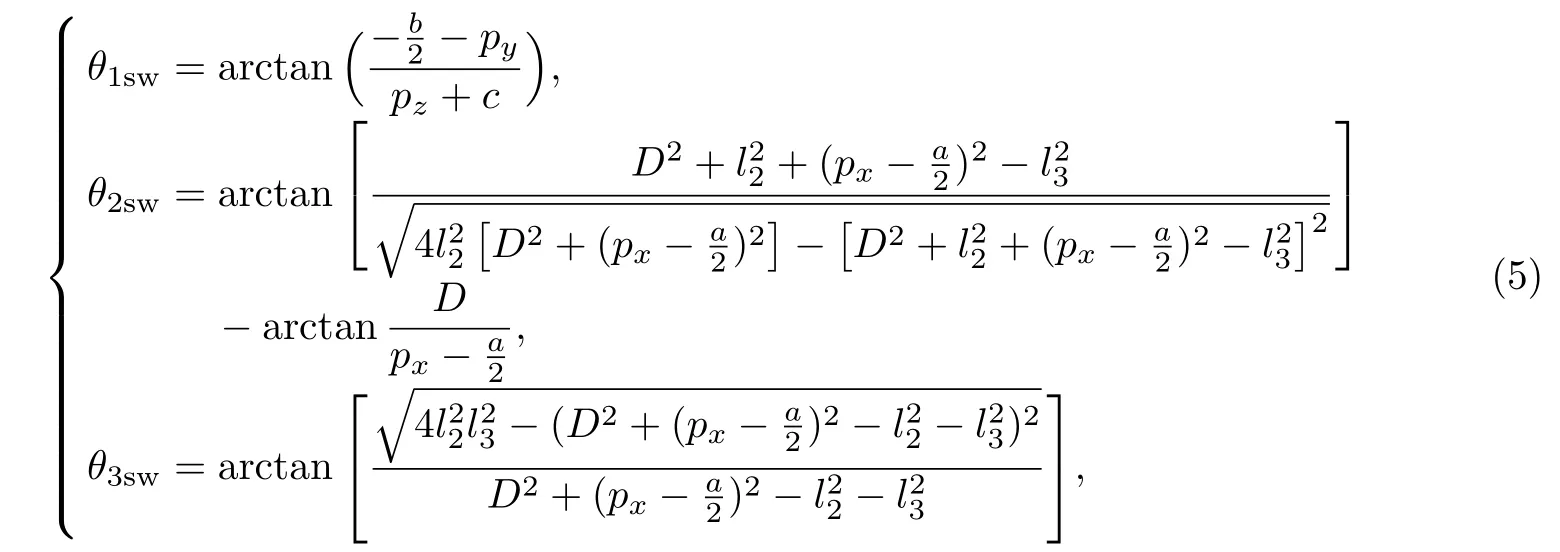
2.2 腿处于支撑相

四足机器人腿处于支撑相的运动学模型为[14]

由式(6)可解得腿处于支撑相时关节角位移函数为

3 对角小跑步态的CPG控制模型

3.1 单关节CPG模型

3.1.1 单个振荡单元模型

建立模型的目的是用数学模型模拟神经元及其相互之间的关联,并建立CPG输出与物理空间映射关系.基于CPG模型控制的核心是构造产生自激振荡,通过对振荡信号的频率、相位、幅值等特性进行调节,控制四足机器人以不同步态方式步行.机器人对外部和内部的反馈信息通过影响振荡信号特性来调节机器人的运动.

在生物神经元的基础上采用一种基于运动神经元CPG模型,神经元振荡单元的信号由一个兴奋神经元和一个抑制神经元通过相互刺激和抑制形成,每个兴奋神经元或者抑制神经元自身存在相同形式的非线性自反馈连接,且二者之间的线性连接强度相同.外部的反馈信号影响兴奋和抑制的作用,如图4所示.

图4 CPG振荡器模型Fig.4 CPG oscillator model

CPG模型方程如下:

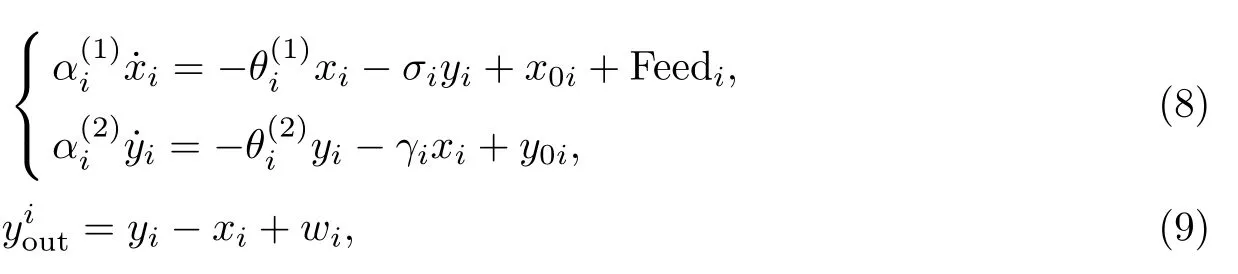
式中:xi,yi为抑制神经元和兴奋神经元;θ为调节系数,这里取为常数;为xi和yi的自抑系数;Feedi为外部传感器给第i个神经元的反馈相;x0i,y0i为初始状态时的值.

对模型进行改进:①用兴奋神经元y和抑制神经元x的差值作为振荡器的输出,=yi−xi+wi,wi为调整系数,在四足机器人的控制中可以用4个改进的神经元模型控制四足机器人的单关节;②引入了反馈相Feedi,反馈相的加入使机器人对外界环境有了适应性,能够根据外界环境调节自身运动,是机器人智能化发展的重要部分;③调整振荡器参数,使振荡器输出信号作为关节角度信号直接控制关节运动,控制方便.

对CPG神经元模型用Simulink进行仿真,观察模型的特性.首先,对模型中的参数赋值:

模型中yi通过与xi互相刺激和抑制使yout获得稳定的振荡输出,如图5所示.给定模型初值x0i=1,y0i=0,可以产生自发稳定的节律振荡,符合振荡源产生的条件.CPG的输出用于控制关节运动.

图5 单个神经元的振荡曲线Fig.5 Oscillator curve of single neuron

3.1.2 模型参数分析

CPG模型能够自发地产生稳定平滑的节律振荡.机器人运动过程通过对振荡信号的频率、相位、幅值等特性进行调节.分析模型中参数,更好地调节振荡信号,控制机器人按照规定运动.当σi=0.4时,振荡信号周期T=10 s;当σi=0.6时,振荡信号周期T=8 s.其他参数值保持不变,改变σi值,振荡信号周期发生规律性变化.由仿真分析可知,σi值不超过1.4,σi可作为振荡信号的周期调节器.调节σi值使振荡信号周期符合规划机器人对角小跑运动周期.上层控制提供x0i,y0i初始状态值给模型,模型发出振荡信号.初始设定x0i=0,y0i=0,模型仿真,振幅A=2.3.改变初值x0i=2,y0i=0,其他参数保持不变进行仿真,振幅A=4.6.多次改变初值x0i后仿真,随着初值变化,振荡信号幅值发生规律性变化,初值可作为振荡信号的振幅调节器.通过改变初始状态值可以对振荡信号振幅进行调整,使之符合机器人腿摆过程.wi作为模型调整系数,对t=0时振荡信号初始值进行调整.反馈信号对模型输出具有调节作用,在加入反馈值后响应曲线幅值偏移相应的值,Feedi值越大,模型幅值越大,这对机器人的自动调节过程是必要的.

3.2 四足机器人对角小跑步行仿真分析

基于CPG控制方法,采用Matlab/Simulink软件对四足机器人对角小跑步态进行仿真分析.四足机器人完成一个对角小跑步行,需4条腿交替处于支撑相和摆动相协调运动.设定步态周期为10 s.四足机器人对角小跑步行时,前5 s,对角线上的腿1和腿3处于摆动相,并开始同时摆动,腿2和腿4处于支撑相.后5 s,腿1和腿3处于支撑相,腿2和腿4处于摆动相.

由于对角小跑步态既要调节机器人四条腿间的相位差,也要调节每条腿上的髋关节和膝关节运动.采用由1个CPG输出控制每条腿上的髋关节,则用4个CPG协调控制4个髋关节,膝关节运动由髋-膝的映射函数确定.CPG模型反映了神经元的自抑制和互抑制特性,调整模型参数,输出正旋轨迹下单腿髋关节和膝关节的控制信号.

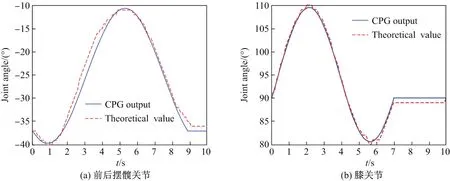
图6 仿生腿关节运动理论分析与仿真结果Fig.6 Theoretical and simulation results of bionic leg

由图6可以看出,基于CPG模型输出的髋关节和膝关节角位移仿真结果与理论分析结果基本一致,验证了理论分析的正确性.仿真结果和理论分析的误差主要是由于未进行CPG控制模型参数的整定,由试凑法获得的参数难免造成CPG模型输出值与理论值不完全一致.这也是CPG控制遇到的难点,后续将开展深入的研究.

4 实验研究

实验时设定四足机器人一个步态周期为5 s,基于CPG控制策略开展对角小跑步态实验研究.实验中所用的电气硬件有电源、电机驱动器、伺服电机、电机编码器等.采用Microsoft Visual Studio作为上位机软件的开发环境,使用C#语言编写程序.个人计算机(personal computer,PC)作为上位机向电机驱动器发送命令,电机驱动器驱动伺服电机,电机编码器实时测量四足机器人关节角度.

四足机器人关节电机作为控制对象,接受驱动器控制.CPG振荡器自激振荡产生振荡信号作为关节角度信号发送给驱动器,调整CPG振荡器参数使之输出T=5 s时四足机器人对角小跑振荡曲线.由电机后端的编码器实时采集关节角度和关节速度信息.四足机器人对角小跑步行时序图如图7所示.

图7 四足机器人对角小跑步态步行时序图Fig.7 Diagram of quadruped robot walking with trot gait

四足机器人前后摆髋关节和膝关节的角位移的理论和实验结果,如图8所示.前后摆髋关节和膝关节角位移的理论与实验结果的误差,如图9所示.

图8 四足机器人对角小跑步态的关节角位移对比Fig.8 Angular displacement of joint of quadruped robot with trot gait

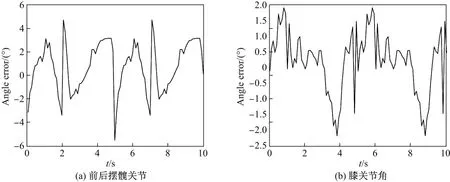
图9 四足机器人对角小跑步态的关节角位移误差Fig.9 Angular displacement error of joint of quadruped robot with trot gait

由图9可以看出,前后摆髋关节和膝关节角位移实验曲线与理论值曲线在极值、变化趋势方面基本一致.髋关节误差范围为[–2,2],在步态周期的末段出现较大误差;膝关节误差范围为[–4,4],在步态周期中段出现较大误差.误差产生的原因有:①足端正弦轨迹,髋关节和膝关节角速度在一个周期中段不平滑,会有跳跃点造成机器人关节振动.髋关节和膝关节角加速度在周期末段存在跳跃点,造成关节振动;②实验采集的数据是编码器返回的脉冲量,驱动器在将输入量转化为控制电机运动的脉冲量时会存在误差,而将编码器返回的脉冲量转化为角度时也会产生误差.

5 结束语

基于中枢模式发生器的控制方法,能够自动产生稳定的节律信号,不仅结构简单,而且具有很强的适应性.本工作开展四足仿生机器人对角小跑步行控制研究,设计了一种四足机器人对角小跑步态控制策略.采用CPG的控制方式建立振荡器模型,以输出的振荡波控制四足机器人关节角度变化.CPG控制策略结构简单,与Matsuoka振荡器、Hop f振荡器、Hodgkin-Huxley振荡器和Van Del Pol振荡器相比,可调参数较少,经过几个周期振荡可实现稳定步态.在四足机器人原理样机上,开展基于CPG模型的四足机器人对角小跑步态步行实验研究,结果表明:CPG控制策略能较好地实现四足机器人对角小跑稳定步行,为提高四足机器人非结构化环境机动性奠定了基础.

[1]边桂彬.BigDog技术分析与展望[J].机器人技术与应用,2012(1):11-13.

[2]孟健,李贻斌,李彬.四足机器人对角小跑步态全方位移动控制方法及其实现[J].机器人,2015,37(1):74-84.

[3]胡楠,李少远,黄丹,等.高负载四足机器人的步态规划与控制[J].系统仿真学报,2014,27(3):529-533.

[4]WANG X,LI M,WANG P,et al.Bio-inspired controller for a robot cheetah with a neural mechanism controlling leg muscles[J].Journal of Bionic Engineering,2012,9(3):282-293.

[5]王健美,付成龙,黄元林,等.基于CPG的仿生机器人运动控制方法及研究进展[J].机械设计与制造,2009,9(9):1-3.

[6]BILLARD A,IjSPEERT A J.Biologically inspired neural controllers for motor control in a quadruped robot[C]//IEEE-INNS-ENNS International Joint Conference on Neural Networks.2000:637-641.

[7]KIMURA H,FUkUOkA Y,KONAGA K.Adaptive dynamic walking of a quadruped robot by using neural system model[J].Advanced Robotics,2001,15(8):859-876.

[8]SIMON R,ALEXANDER S,LUDOVIC R,et al.Passive compliant quadruped robot using central pattern generators for locomotion control[C]//IEEE Ras&Embs Intemational Conference on Biomedical Robotics and Biomeehatronics.2008:710-715.

[9]CHRISTOPHE M,HIROSHI K,TOMOHIRO N.Stable dynamic walking of the quadruped “kotetsu”using phase modulations based on leg loading/unloading against lateral perturbations[C]//International Conference on Robotics and Automation Saint Paul.2012:1883-1888.

[10]李彬,李贻斌,阮久宏,等.基于Wilson-Cowan神经振荡器的四足机器人步态规划研究[J].山东大学学报(工学版),2010,40(1):1-10.

[11]张美金,杜晶,陈明霞.基于中枢模式发生器的仿生机器狗步态控制的应用研究[J].计算机测量与控制,2012,20(5):1245-1247.

[12]韩青,任杉,曹飞祥,等.中枢模式调节的四足机器人复杂地形运动控制研究[J].制造业自动化,2013,35(9):25-29.

[13]HUTTER M,REMY C D,HOEPFLINGER M A,et al.Design and control of a planar running robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.2011:562-567.

[14]LEI J T,WANG F,YU H Y,et al.Energy eきciency analysis of quadruped robot with trot gait and combined cycloid foot trajectory[J].Chinese Journal of Mechanical Engineering,2014,27(1):138-145.