植物带影响下孤立波沿程波高衰减特性试验

何 飞,陈杰,2,3, 蒋昌波,2,3,赵 静

(1. 长沙理工大学水利工程学院,湖南 长沙 410114; 2. 水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114;3. 长沙理工大学水科学与环境工程国际研究中心,湖南 长沙 410114)

海啸是一种破坏力极强的海浪,2004年印度洋海啸灾难发生后,植物消波已成为近年来海岸工程研究的热点[1]。观测表明,海啸波的首波与孤立波非常接近,因此目前学术界多采用孤立波来近似模拟海啸波[2]。关于近岸植被影响下的孤立波传播变形研究对近岸植被消波减灾具有重要的理论指导意义。国内外学者对于近岸植被影响下的波浪传播变形开展了大量研究。关于近岸植被作用下规则波传播变形理论主要有Kobayashi等[3]基于动量守恒方程和线性波理论得出的指数函数衰减规律以及Darlymple等[4]基于能量守恒方程和线性波理论得出的幂函数式衰减规律。众多研究结果[5-7]与上述近岸植被中波浪传播变形规律基本一致,而关于近岸植被对于孤立波传播变形的影响尚未形成系统的理论。部分学者通过数值模拟探究近岸植被与孤立波的相互作用机理,其研究均未考虑植物冠部因素。如Maza等[8]基于IHFOAM数值模型,探究了刚性植物对于孤立波传播变形的影响,而Huang等[9]则通过Boussinesq方程模拟了不同宽度植物带影响下的孤立波传播变形。另一部分学者从物理模型试验入手,探究植物带影响下的孤立波反射、透射、波能耗散以及爬高变化规律。王俊[10]利用PVC管模拟红树林,探讨了孤立波与红树林植物模型相互作用时透射波和反射波的变化情况,而蒋昌波等[11]则探究了红树林植物模型前后孤立波波形变化以及入射波波高和分布密度对孤立波反射、透射和波能衰减系数的影响。Husrin等[12]和Hashim等[13]分析了红树林树根对于孤立波传播变形的影响。姚宇等[2]探究了斜坡上非淹没刚性植物与孤立波的相互作用,分析了入射波波高和植被密度对孤立波斜坡爬高的影响。尽管上述学者针对孤立波与近岸植被相互作用开展了大量数值模拟及物理模型试验,但对于孤立波在近岸植被中传播变形规律的研究较少。更为重要的是,近岸植被消减孤立波过程中,根茎叶均在不同程度上发挥作用,而上述研究均将植物根茎叶作为独立因素探究其对孤立波传播变形的影响,孤立波在根茎叶共同影响下的近岸植被中传播变形规律的研究尚未见报道。因而,综合考虑根茎叶影响的孤立波沿程波高衰减特性有待进一步探讨。

图1 试验布置(单位:cm)

本文拟在前人的研究基础之上,综合考虑植物根茎叶的影响,开展近岸植被对孤立波传播变形影响的试验研究。

1 理论分析

1.1 Kobayashi指数函数波高衰减模型

波浪在植物带中传播时,在植物作用下波能将衰减。在线性波理论前提下,Kobayashi等[3]指出波浪的自由液面满足下式：

(1)

式中:H0为x=0处波高;β为波能衰减系数;x为植物带中沿流向的水平坐标；k为波数;σ为角频率；t为时间。假设微幅波以相速在植物带中传播,波速c=σ/k，实际沿程波高衰减将满足

H=H0exp(-βx)

(2)

1.2 Dalrymple幂函数波高衰减模型

假设波浪传播满足线性波理论,根据能量守恒方程,可得植物带中波高衰减应满足

(3)

式中:E为能量密度；ρ为流体密度;g为重力加速度;cg为波群速度;εv为波能衰减项。

Dalrymple等[4]将植物带中波能衰减项表达为

(4)

式中:CD为植物拖曳力系数；bv为单株植物迎浪面宽度;N为单位面积植物株数;hs为植物淹没高度;h为水深。

对于平底植物带消波模型,将式(4)代入式(3)可得

(5)

对于上述微分方程(5),给定边界条件H(x=0)=H0,可求得植物带沿程波高衰减规律为

(6)

2 试验方案

试验在长沙理工大学波浪水槽内进行,水槽长40.0 m,宽0.5 m,高0.8 m。试验布置如图1所示。

图2 植物模型

根据陈杰等[14-15]对我国相关防浪植物带的调查资料,结合Mazda等[16]对相关树种树根的调查资料,同时考虑到试验室仪器条件限制,设计试验所需要的植物模型。如图2所示,本试验采用的几何比尺为1∶10。刚性植物模型树干部分采用PVC圆管,PVC管直径为1.1 cm。PVC管在波浪作用下不会产生明显的变形,可较好地模拟植物树干(刚性)部分。植物树冠部分带有较多枝杈,表现出较好的柔性,本试验选取了聚乙烯材料模拟植物树冠,冠部直径为10.0 cm,冠部高度为20.0 cm。由于树根根须数量、根须直径、对底面投影面积等因素非常复杂,本试验对植物根部仅作概化处理,采用具有一定柔性的塑料球架模拟植物根部,在模拟试验中塑料球架与波浪相互作用时没有较明显的变形,可以较好地模拟植物树根部分。同时为更好地模拟根部的复杂性,将塑料球架裁剪成一大一小两种尺寸,小尺寸球架放置于内部,大尺寸放置于外部, 根部外层直径为8.0 cm,根部垂直高度为5.0 cm。

为便于将植物安置在水槽底部,制作有机玻璃底板用于固定植物模型。底板尺寸为150.0 cm×48.0 cm×0.8 cm(长×宽×高),在板上以孔间距2.5 cm穿孔。考虑到植物冠部(叶)及根部(根)几何特征的复杂性,采用树干(茎)横截面积之和与底板面积的比值来定义植物分布密度:

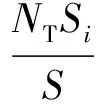
(7)

式中:NT为分布区域内的植物总株数;Si为单株植物横截面面积;S为整个分布区域面积。试验中模型均以正方形分布方式布置,可得到不同的植物分布密度。

图3 植物模型分布方式(单位：cm)

如表1所示,考虑到实际情况中的波况及试验仪器限制,试验水深h分别为25.0 cm、30.0 cm、35.0 cm和45.0 cm,入射波波高H分别为5.0 cm、9.0 cm和12.0 cm。如图3所示,为了对比分析植物根茎叶对消波特性的影响,模型1至模型4的分布密度保持一致(ψ=0.009 9),模型1仅对茎进行模拟,模型2

表1 试验工况

对茎和根进行模拟,模型3对茎和叶进行模拟,模型4对根茎叶都进行模拟。为了讨论分布密度对孤立波沿程波高衰减特性的影响,模型5和6均对根茎叶进行模拟,分布密度分别为0.006 3和0.004 0。

试验首先放置植物模型,随后对造波机预热,保证造波机性能稳定,再开启数据采集系统,确保浪高仪性能良好。调整水槽中水位至试验水位,待水面平静后开始造波,并测量波高数据。波高测量采用加拿大WG-50型浪高仪。浪高仪最小测量周期为1.5 μs,误差为0.4%,采样频率为50 Hz。对于孤立波,试验数据采集从造波机造波开始,到孤立波传播过程结束。完成一个组次试验后,需待水面平静后,再进行下一次造波,重复上述步骤完成下一组次试验。

为了便于分析定义植物淹没度

(8)

式中：hv为植物垂直高度。

同时定义H1为x=1.5 m处(植物带末端)波高,Hi为植物带沿程各浪高仪测点处波高,H1/H0表征了孤立波沿程波高衰减强度;Hi/H0表征了孤立波沿程波高衰减变化。

3 结果分析

3.1 Kobayashi指数函数和Darlymple幂函数衰减规律

本文孤立波沿程波高衰减强度Hi/H0变化范围为0.52～0.93,对应的Kobayashi指数函数的波能衰减系数β理论值变化范围为0.05～0.43,所对应的Dalrymple幂函数的β理论值变化范围为0.05～0.61,据此给出由本文试验得到的Kobayashi指数函数和Dalrymple幂函数衰减规律(图4)。

图5 茎影响下孤立波沿程波高衰减规律

图4 Kobayashi指数函数和Dalrymple幂函数衰减规律(本文数据)

结果显示,当植物带沿程波高衰减剧烈时(β=0.43和0.61),Kobayashi指数函数和Dalrymple幂函数衰减规律都反映出植物带波能衰减更集中于植物带前半部分的特性。正如Snchez-Gonzlez等[6]所指出的,Kobayashi指数函数和Dalrymple幂函数衰减规律均反映出波浪从平底区域传播至植物带区域时在植物带前半部分所产生波能剧烈衰减现象,即植物带消波的边界效应。从图中可以看出,β越大,植物带消波的边界效应越强。

3.2 茎影响下孤立波沿程波高衰减特性

图5分别给出本文、Maza等[8]以及Huang等[9]的研究中茎作用下孤立波沿程波高衰减规律,其中图5(a)(b)(c)的植物分布方式为正方形布置，图5(d)的植物分布方式为对角线布置。从图5(a)(b)可以看出，在本文试验中,仅当波浪非线性H/h=0.11时,沿程波高服从指数函数分布,植物带消波呈现明显的边界效应。其余波况下(H/h>0.11),Hi/H0对x/L的敏感度随x/L的增大而增强,即随着孤立波向近岸传播,其衰减强度增强,植物带消波无边界效应存在。从图5(c)可以看出，在Maza等[8]的研究中,H/h=0.17和0.33时孤立波沿程波高衰减规律与本文H/h=0.48情况一致,而当H/h=0.67时,沿程波高衰减则满足指数函数或幂函数规律衰减,植物带消波具有边界效应。孤立波沿程波高衰减特性与其H/h相关;而从图5(d)可以发现,在Maza等[8]的研究中,当植物满足对角线分布方式时,孤立波沿程波高衰减满足指数衰减规律,植物带消波具有明显的边界效应,而Huang等[9]的试验中沿程波高衰减则更接近于Maza等[8]的研究中正方形分布所得的衰减规律。

综上所述,本文所得的孤立波沿程波高衰减规律依赖于H/h,这与Maza等[8]研究结果一致。尽管Huang等[9]与Maza等[8]的植物分布方式不同,但是当孤立波非线性相近时,Maza等[8]与Huang等[9]所得植物带沿程波高衰减规律却基本一致,这表明相比植物分布方式,孤立波的非线性强弱是沿程波高衰减特性的主要影响因素。

图6 根影响下孤立波沿程波高衰减规律

3.3 根影响下孤立波沿程波高衰减特性

图6给出了模型2(茎+根)对比模型1(茎)作用下孤立波沿程波高衰减规律试验结果。对比模型1和模型2试验结果可以看出,淹没度α=0.56时,根主要对弱非线性(H/h=0.20和0.36)孤立波沿程波高衰减趋势产生影响,而对强非线性(H/h=0.48)孤立波,仅增强其在末端2/3部分(1/3

3.4 叶影响下孤立波沿程波高衰减特性

图7为模型3(茎+叶)对比模型1(茎)作用下孤立波沿程波高衰减规律的试验结果。对比模型3和模型1试验结果可以看出,淹没度α=0.56时,叶明显改变强非线性(H/h=0.36和 0.48)孤立波沿程波高衰减趋势,植物带消波呈现边界效应;而α=0.67时,叶明显改变强非线性(H/h=0.30和0.40)孤立波沿程波高衰减趋势,植物带消波具有边界效应;α=0.78时,叶仅改变H/h=0.26的孤立波沿程波高衰减趋势,植物带消波呈现出边界效应;与上述情况不同的是,α=1.00条件下叶明显改变弱非线性(H/h=0.11)孤立波沿程波高衰减趋势,植物带末端1/3部分(2/3

3.5 根茎叶影响下孤立波沿程波高衰减特性对比

不同淹没度情况下入射波波高H=9 cm时模型1(茎)、模型2(茎+根)、模型3(茎+叶)以及模型4(茎+根+叶)作用下孤立波沿程波高衰减的试验结果见图8。从图8可以看出,根在一定程度上改变孤立波沿程波高衰减强度,根茎共同作用下的孤立波沿程波高衰减强度H1/H0最小约为茎单独作用下的96%,但并未改变波高衰减趋势,茎以及根茎共同作用下的孤立波沿程波高衰减特性与指数函数或幂函数规律并不一致。与上述情况不同的是,茎叶共同作用下的H1/H0最小约为茎单独作用下的55%。当植物处于非淹没状态(α<1.00)时,叶的存在明显改变了波高衰减趋势,使得孤立波沿程波高衰减满足上述衰减规律,此时植物带消波存在明显的边界效应。此外,根茎叶共同作用下孤立波沿程波高衰减强度最大,此时植物带消波效果最好。这也进一步说明,在探究植物带影响下孤立波沿程波高衰减特性时应综合考虑根茎叶因素。综上所述,相比根和茎,叶对孤立波沿程波高衰减特性影响较大。

图7 叶影响下孤立波沿程波高衰减规律

图8 根茎叶影响下孤立波沿程波高衰减规律对比

图9 不同淹没度下分布密度ψ对孤立波沿程波高衰减特性的影响

3.6 分布密度对孤立波沿程波高衰减特性的影响

图9分别给出不同淹没度情况下植物分布密度对孤立波沿程波高衰减特性的影响。试验结果显示,α=0.56时(图9(a)),当分布密度ψ由0.009 9减小至0.004 0时植物带沿程波高衰减趋势并无明显改变,但ψ的减小减弱了孤立波沿程波高衰减强度,此时其沿程波高衰减服从指数函数衰减规律,植物带消波呈现明显的边界效应;α=0.67时(图9(b)),当ψ由0.009 9减小至0.004 0时,对于弱非线性(H/h=0.17和0.30)孤立波,ψ的减小明显改变其沿程波高衰减趋势。但强非线性(H/h=0.40)孤立波沿程波高衰减则始终满足指数衰减规律,植物带消波存在边界效应;α=0.78时(图9(c)),与ψ=0.009 9不同的是,ψ较小(ψ=0.006 3和0.004 0)时,强非线性(H/h=0.34)孤立波波高衰减集中于植物带中间部分(1/3

4 结 论

本文通过物理模型试验探究了植物带影响下的孤立波沿程波高衰减特性。试验结果表明,根茎叶及分布密度对孤立波沿程衰减特性的影响与淹没度α和孤立波非线性H/h相关。H/h>0.11时,茎影响下孤立波沿程波高衰减特性与Kobayashi指数函数以及Darlymple幂函数规律并不一致,出现随着孤立波向近岸传播,其波高衰减强度增强的现象,植物带消波无边界效应存在;α=0.67时,根茎共同作用与茎单独作用下孤立波沿程波高衰减趋势基本一致;α小于0.67且H/h不小于0.30时,茎叶作用下孤立波沿程波高衰减服从指数函数和幂函数衰减规律,植物带消波呈现边界效应;根茎共同作用下的孤立波沿程波高衰减强度H1/H0最小约为茎单独作用下的96%,而茎叶共同作用下的H1/H0最小约为茎单独作用下的55%,相比根茎,叶对孤立波沿程波高衰减特性影响更大。非淹没情况下(α<1.00),随着分布密度的减小,孤立波沿程波高衰减强度减小,植物带消波边界效应减弱。

[ 1 ] 陈杰, 蒋昌波, 邓斌,等. 海啸波作用下岸滩演变与床沙组成变化研究综述[J]. 水科学进展, 2013, 24(5):750-758. (CHEN Jie, JIANG Changbo, DENG Bin, et al. Review of beach profile changes and sorting of sand grains by tsunami waves[J]. Advance in Water Science, 2013, 24(5):750-758. (in Chinese))

[ 2 ] 姚宇, 杜睿超, 袁万成,等. 斜坡非淹没刚性植被影响下孤立波爬高的研究[J]. 水动力学研究与进展, 2015, 30(5):506-515. (YAO Yu, DU Ruichao, YUAN Wancheng, et al. Investigation of solitary wave runup on a slope under the effect of emergent, rigid vegetation [J]. Chinese Journal of hydrodynamics, 2015, 30(5):506-515. (in Chinese))

[ 3 ] KOBAYASHI N, RAICHLE A W, ASANO T. Wave attenuation by vegetation[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1993, 119(1):30-48.

[ 4 ] DALRYMPLE R A, KIRBY J T, HWANG P A. Wave diffraction due to areas of energy dissipation[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1984, 110(1):142-150.

[ 5 ] WU W C, COX D T. Effects of wave steepness and relative water depth on wave attenuation by emergent vegetation[J]. Estuarine Coastal & Shelf Science, 2015, 164:443-450.

[ 7 ] MARSOOLI R, WU W. Numerical investigation of wave attenuation by vegetation using a 3D RANS model[J]. Advances in Water Resources, 2014, 74:245-257.

[ 8 ] MAZA M, LARA J L, LOSADA I J. Tsunami wave interaction with mangrove forests: a 3-D numerical approach[J]. Coastal Engineering, 2015, 98:33-54.

[ 9 ] HUANG Z, YAO Y, SIM S Y, et al. Interaction of solitary waves with emergent, rigid vegetation[J]. Ocean Engineering, 2011, 38(10):1080-1088.

[10] 王俊. 海岸红树林与海啸波相互作用的实验研究[J].广东水利电力职业技术学院学报, 2011, 9(3):1-4. (WANG Jun. Experimental study on interactions of tsunami wave with coastal mangrove forest [J]. Journal of Guangdong Technical College of Water Resources and Electric Engineering, 2011, 9(3): 1-4. (in Chinese))

[11] 蒋昌波,王瑞雪,陈杰,等.非淹没近岸植物对孤立波传播变形影响实验[J].长沙理工大学学报(自然科学版), 2012, 9(2): 51-56. (JIANG Changbo, WANG Ruixue, CHEN Jie, et al. Laboratory investigation on solitary wave transformation through the emergent neritic vegetation [J]. Journal of Changsha University of Science and Technology (Natural Science), 2012, 9(2): 51-56. (in Chinese))

[12] HUSRIN S, STRUSISKA A, OUMERACI H. Experimental study on tsunami attenuation by mangrove forest[J]. Earth, Planets and Space, 2012, 64(10):973-989.

[13] HASHIM A M, CATHERNE S M P. A laboratory study on wave reduction by mangrove forests [J]. Apcbee Procedia, 2013, 5:27-32.

[14] 陈杰, 赵静, 蒋昌波,等. 非淹没刚性植物对规则波传播变形影响实验研究[J]. 海洋通报, 2017, 36(2):222-229. (CHEN Jie, ZHAO Jing, JIANG Changbo,et al. Laboratory investigation on the effects of emergent rigid vegetation on the regular wave transformation[J]. Marine Science Bulletin, 2017, 36(2):222-229. (in Chinese))

[15] 陈杰, 何飞, 蒋昌波,等. 规则波作用下刚性植物拖曳力系数实验研究[J]. 水利学报, 2017, 48(7):846-857. (CHEN Jie, HE Fei, JIANG Changbo, et al. Experimental investigation on drag coefficient of rigid vegetation influenced by regular waves[J]. Journal of Hydraulic Engineering, 2017, 48(7): 846-857. (in Chinese ) )

[16] MAZDA Y, WOLANSKI E, KING B, et al. Drag force due to vegetation in mangrove swamps[J]. Mangroves & Salt Marshes, 1997, 1(3):193-199.