翻板抛投土工包沉落轨迹与落域
刘欣欣,束一鸣,顾 克,王晓娟
(1.北京矿冶研究总院矿山工程研究设计所,北京 102628; 2.河海大学水利水电学院,江苏 南京 210098;3.河海大学土木与交通学院,江苏 南京 210098; 4.南京市滁河河道管理处,江苏 南京 210048)
土工包是以高强土工织物制成的呈“枕状”或“箱状”的大体积土工包容系统,其中可充灌砂土、疏浚物等。土工包体积大,整体性好,可用于水工结构或海岸工程,形成大块平台、堤岸或围垦土地[1-4]。最早利用土工包进行河岸治理和水下结构物填筑的是1988年荷兰Old Meuse河的修复工程,包括修复水下边坡和水下防波堤的填筑,将233个单体为200 m3的充砂土工包用开底驳船投放到一定部位(深20 m),并依次堆叠起来,形成水下结构。采用土工包填筑潜堤堤芯的构筑形式,已在美国多项工程中应用,包括新奥尔良的Red Eye Crossing工程[5]和洛杉矶的Marina Del Rey工程[6]。
土工包的体积相差悬殊。较小的土工包体积不过数十立方米,而大的土工包可达上千立方米。小的土工包可以在岸上充填和缝合,然后用船或自卸汽车运输和投放。对于体积巨大的土工包,一般是在开底驳船上完成充填和投放,但该施工方法容易造成包体撕裂[7-9]。利用船舷翻板充填投放土工包的施工方法,可多包同时充填投放,施工效率较高且不易破包。由于受土工包体积、充填率、滑落长度、翻板倾斜角度、水深和流速等因素的影响,抛投包体的落点随机性很大,效率低下,目前工程界大多采用试抛的方法粗略判断土工包落域,施工精度和效率仍然偏低[10-13]。因此,需要研究翻板抛投土工包的沉落机理,以总结土工包落域的定量计算方法。
关于土工包沉落规律,目前已有部分研究成果。Zhu等[14]对驳船投放土工包的沉落规律进行了研究,提出了土工包落点距离的计算公式,计算结果与现场试验误差小于17%。应强等[15]假定土工包平行下沉、无转动,根据牛顿第二定律建立了土工包的运动微分方程。杨素勤[16]研究了土工包在沉落过程中受水流影响产生的位移特征,对土工包的沉落规律进行了归纳,提出了计算土工包沉落位移的经验公式。上述研究成果仅适用于计算水平静止状态下投放的土工包,不适用于采用船体翻板投放的土工包。土工包从船体翻板上滑落,具有一定的入水角度和入水速度,目前尚未见其沉落运动过程计算方法的研究报道。
针对上述问题,本文采用物理模型水槽开展土工包滑抛试验,对翻板投放的“枕状”土工包的沉落规律进行了研究,建立了一种用于翻板滑抛土工包沉落轨迹与落域的理论计算模型,可为工程设计和施工提供理论依据。
1 沉落运动方程
“枕状”土工包几何模型如图1所示。该土工包由一整块丙纶布对折缝合而成,在短边预留填砂口,装填完成后缝合。缝合后的填砂口横断面近似椭圆形,椭圆大小与充填率φ有关。假设填砂口的周长为D,土工包的长度(长轴方向)为B,规定土工包的尺寸统一采用D×B表示,则椭圆长轴d1、短轴d2和土工包体积V可分别表示为
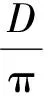
(1)
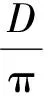
(2)
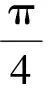
(3)
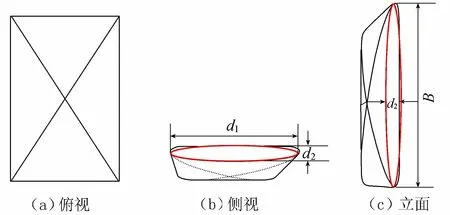
图1 “枕状”土工包几何模型
土工包从翻板上滑动并在水槽中沉落的全过程如图2所示。水槽中水深为H,沿x方向的均匀流速为u。通过观察预试验结果,对于尺寸D×B=16 cm×12 cm(原型尺寸为8 m×6 m)、充填率φ=78.54%的土工包,其沉落运动过程规律性较好,可将其近似分为3个阶段:翻板滑落阶段(第一阶段)、入水角水平转变阶段(第二阶段)和水平沉落阶段(第三阶段)。
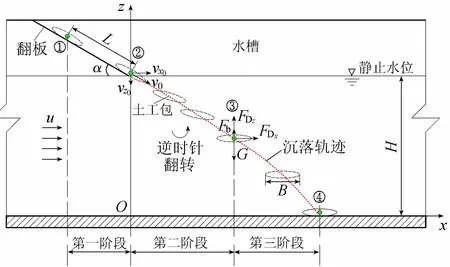
图2 土工包在水槽中的沉落运动过程
在第一阶段,土工包从翻板上由①位置静止滑落至②位置。假定翻板倾斜角度为α,摩擦系数为μ,滑落距离为L,则在②位置,土工包初始速度及在x、z方向的初始速度分别为
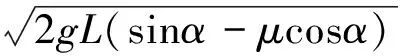
(4)
vx0=v0cosα
(5)
vz0=v0sinα
(6)
在第二阶段,土工包从②位置运动至③位置,土工包入水角度逐渐减小,到达③位置时,土工包的长轴方向近似水平。值得注意的是,第二阶段一般较为短暂,为便于分析,假定土工包入水瞬间其长轴方向便保持水平。
在第三阶段,土工包基本保持水平状态下沉,直至触底到达④位置。其中,土工包②位置与④位置之间的水平距离,称之为沉落距离S,该参数是抛投施工中移船定位的重要依据。触底后,土工包一般会向前滑动一段距离,对于该过程的计算,本文暂未涉及。在③位置,土工包近似水平,此时其受力包括x方向水流推动力Fdx和z方向的重力G、浮力Fb、水流阻力Fdz:
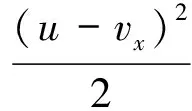
(7)
G=ρsVg
(8)
Fb=ρVg
(9)
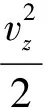
(10)
根据力的平衡原理,土工包在x轴和z轴方向上应保持受力平衡,则有:
(11)
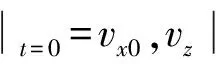
(12)
(13)
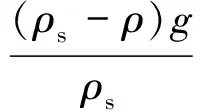
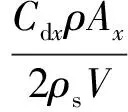
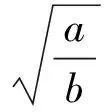
式中:ρs、ρ分别为充填物和水的密度;Cdx、Cdz分别为水平向和竖向的阻力系数;Ax、Az分别为土工包在x轴及z轴方向上的投影面积;u为流速;vx、vz分别为土工包横向和纵向沉落速度;vz∞为终端沉落速度;t为时间;g为重力加速度。

图3 水槽物理模型试验装置
2 物理模型试验设计

试验开始时,首先调节水深和流速,待水流稳定后打开录像机,将土工包浸湿后放置于翻板上,在一定位置处由静止下放,录像机用于记录土工包的下沉轨迹,待土工包落底稳定后关闭录像机,完成一组试验,每组工况重复抛投10次。根据水深和流量的不同组合,试验设计了25组不同工况,如表1所示。
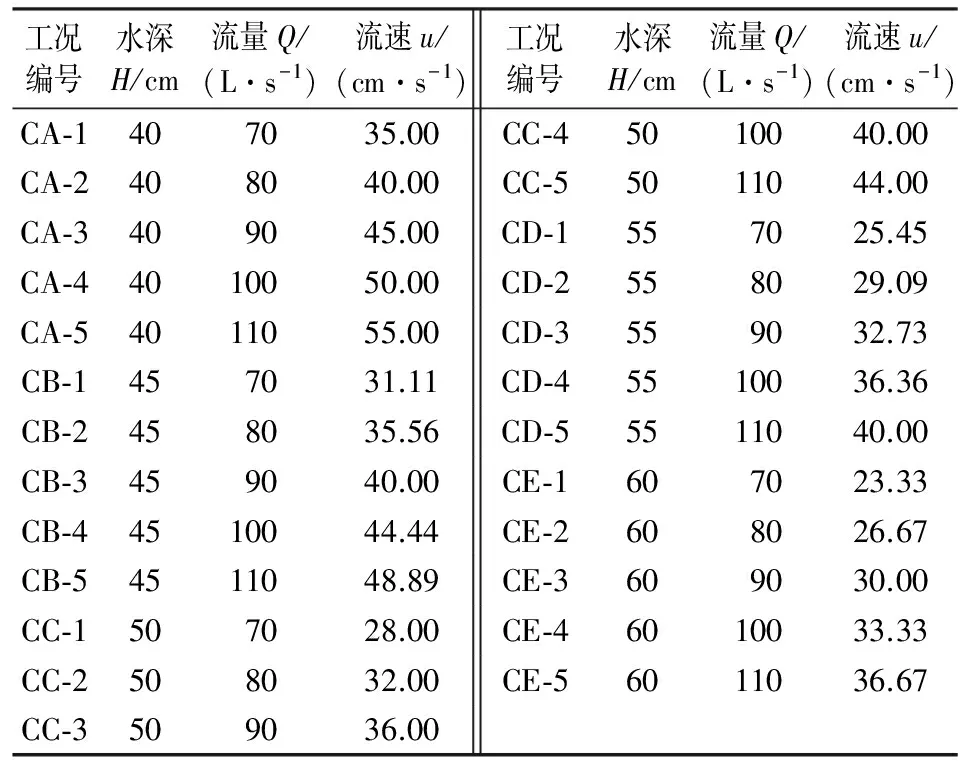
表1 物理模型试验工况
3 试验数据分析方法与结果
3.1 数据分析方法
以物理模型试验为基础,采用间接法求解单包的水平与竖向阻力系数。由式(12)和(13)可知,对于任意给定的一组阻力系数Cdx和Cdz,均可利用这两个公式计算出土工包在时刻t的理论坐标(xp(t),zp(t));假定在相同的工况条件下,由物理模型试验得到时刻t的实际坐标为(xm(t),zm(t));若对于某一组阻力系数Cdx和Cdz,任意时刻土工包的理论坐标与实际坐标都足够接近,则可以认为该组阻力系数值满足计算要求,为最优解。基于上述分析,首先确定目标函数:
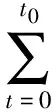
(14)
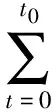
(15)
式中:t0为土工包的总沉落时间。在试验数据的基础上,采用通用非线性最优化计算方法即可计算出对应目标函数gx、gz的阻力系数Cdx和Cdz。
对于土工包,将其雷诺数定义为
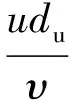
(16)

式中:Reu为土工包的雷诺数;du为土工包的特征尺度,等于土工包的等体积球体直径;υ为水的动力黏滞系数。根据式(16),分别计算出对应不同工况的雷诺数,进而拟合出两种阻力系数与雷诺数的定量关系,结果如图4所示。
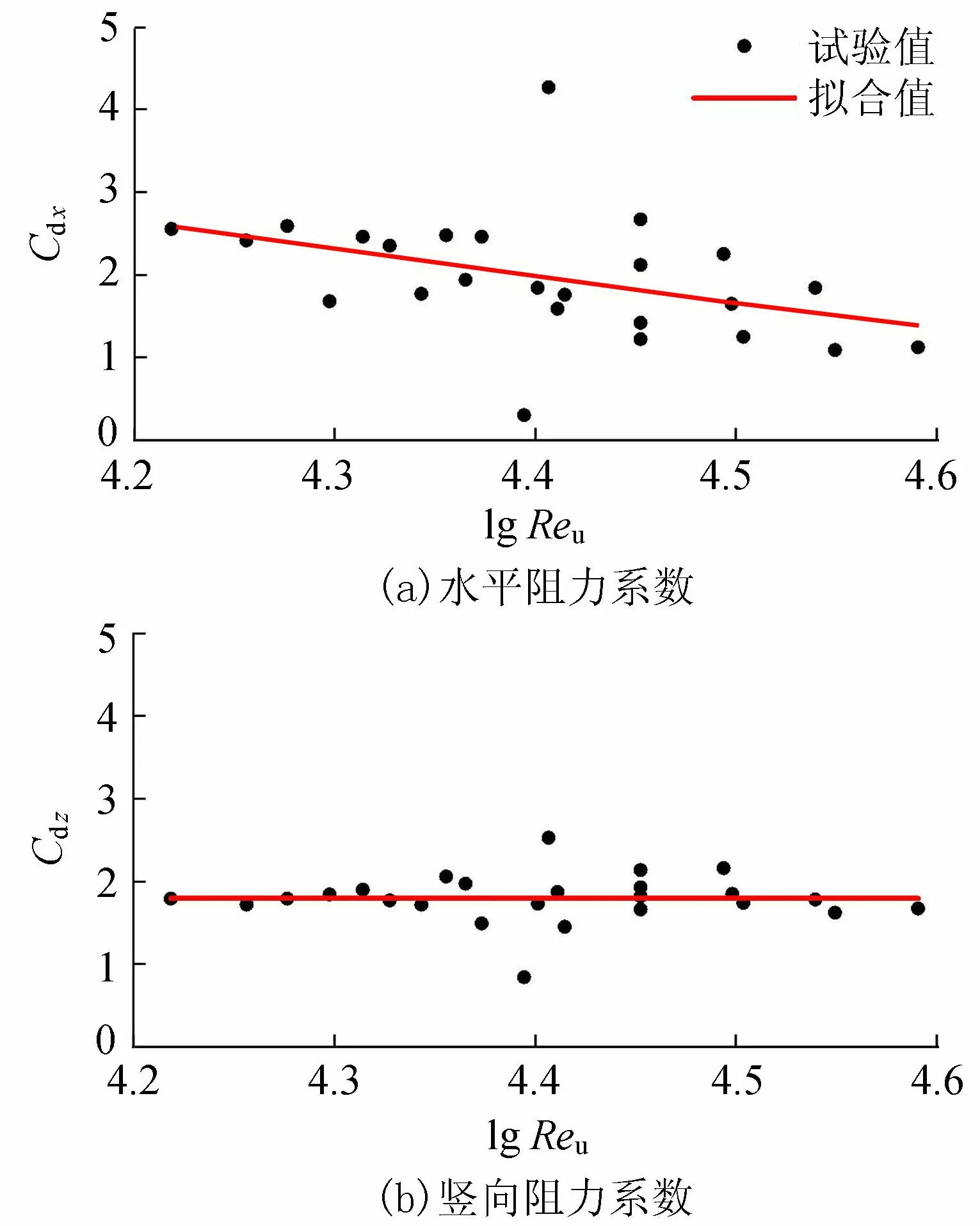
图4 单包阻力系数与物体雷诺数的定量关系
从图4(a)可以看出,水平阻力系数在0.30~4.27之间变化,除两个偏差较大的数值之外,随着雷诺数的增加,水平阻力系数呈现递减趋势;从图4(b)可以看出,对于竖向阻力系数,其变化范围为0.84~2.53,其数值随雷诺数变化不显著,整体趋于一恒定数值。根据上述特征,选取一定的拟合函数,可以得到两种阻力系数的表达式
(16 535≤Reu≤38 977)
(17)
Cdz=1.793 6 (16 535≤Reu≤38 977)
(18)
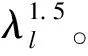
3.2 试验结果
当拟合出阻力系数公式后,土工包沉落轨迹理论计算模型就已完善,通过式(12)~(18),可定量计算单包的沉落轨迹。需要注意的是,实际运用该理论计算模型时,需满足一定的限定条件。相应的抛投参数必须与最优抛投参数保持一致。在此抛投参数的基础上,任意给定一组施工水深(20~30 m)与流速(1.65~3.89 m/s)组合,便可以定量计算出土工包的沉落轨迹与水平落距,为抛投施工时移船定位提供指导。
为验证理论计算模型的可靠性,将理论计算结果与实际抛投结果相对比,以分析二者之间的差异以及产生差异的原因。通过对比,不仅能够验证理论计算模型的可靠性,还可以进一步完善理论计算模型。由于缺少实际抛投施工数据,此处采用物理模型试验结果作为对比对象,基本方法为:在最优抛投参数的基础上,将物理模型试验中的25组工况代入到理论计算模型中,计算出单包的理论沉落轨迹,并将其与物理模型试验沉落轨迹进行对比。图5为部分土工包抛投理论与试验沉落轨迹对比,可以看出:
a. 从沉落轨迹的外部形态上来看,理论与试验沉落轨迹之间存在一定的差异。理论沉落轨迹整体呈抛物线形状,而试验沉落轨迹表现出明显的曲率变化。造成以上差异的原因主要有:①沉落过程中土工包在水平面内发生旋转,由此引起受力面积变化,进而影响受力并最终反映到沉落轨迹上;②垂线流速分布的影响,理论计算模型中假定垂线流速均匀分布,与实际状况不同,故而则土工包的受力状况也存在一定的差异。

图5 土工包抛投理论与试验沉落轨迹对比
b. 水深较浅时,理论与试验沉落轨迹吻合度较高,随着水深的增加,试验沉落轨迹曲率增加,与理论沉落轨迹之间的形态差异开始变大,表明相对于深水条件,理论模型在浅水环境中能取得较好的应用效果。
c. 对于沉落轨迹的分布趋势,理论与试验结果之间存在明显的共性,例如水深一定时,随着流速的增加,水平落距逐渐增加,沉落轨迹逐渐向外侧分散。
4 结 论
a. 基于实际工程中翻板滑抛土工包的施工过程,采用物理模型水槽开展土工包抛投试验,通过研究沉落过程中土工包的运动规律,提出了土工包落点坐标的理论计算公式以及阻力系数的经验计算公式,从而构建出土工包沉落轨迹理论计算模型。
b. 在实际工程中,采用填砂口周长8 m、长度6 m、充填率为78.54%的土工包,选定2.5 m的滑落距离且翻板倾斜角度定为40°,此时翻板抛投的土工包沉落规律性较好,该组参数适可作为一组最优施工参数。
c. 对于工程中通常所用的填砂口周长8 m、长度6 m、充填率为78.54%的土工包,其水平阻力系数的变化范围为0.30~4.27,竖向阻力系数在0.84~2.53之间变化。
d. 水深一定,流速越大,土工包的落点距离越大。当水深较大时,土工包容易发生翻转,消耗掉一部分能量,导致落点距离减小且落点分散,公式计算误差加大。因此,深水大流速工况对土工包抛投施工不利。
[ 1 ] KORKUT R,MARTINEZ E J,MORALES R,et al.Geobag performance as scour countermeasure for bridge abutments[J].Journal of Hydraulic Engineering,2007,133(4):431-439.
[ 2 ] 李凯双,胡殿才,李顺利,等.袋装砂筑堤技术在滩海、浅海工程中的应用[J].石油工程建设,2011(1):20-25.(LI Kaishuang,HU Diancai,LI Shunli.Application of diking technique with sandbag in beach and shallow water engineering [J].Petroleum Engineering Construction,2011(1):20-25.(in Chinese))
[ 3 ] 陆付民,李建林.崩岸的形成机理及防治方法[J].人民黄河,2005(8):16-17.(LU Fumin,LI Jianlin.Mechanism of bank collapse and control methods [J].Yellow River,2005(8):16-17.(in Chinese))
[ 4 ] 束一鸣.我国管袋坝工程技术进展[J].水利水电科技进展,2018,38(1):1-11. (SHU Yiming.Advances in technology of geotube dam engineering in China[J].Advances in Science and Technology of Water Resources,2018,38(1):1-11. (in Chinese))
[ 5 ] BERILGEN S A,BULUT B T.Laboratory investigations for dewatering of golden horn dredged sludge with geotextile tubes[J].Marine Georesources & Geotechnology,2016,34(7):638-647.
[ 6 ] LIU X,SHU Y,GU K,et al.Determination of drag coefficients for settling geocontainers dumped from a bevel[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,2016,143(3):04016024.
[ 7 ] LAWSON C R.Geotextile containment for hydraulic and environmental engineering[J].Geosynthetics International, 2008,15(6):384-427.
[ 8 ] YAN S W,CHU J.Construction of an offshore dike using slurry filled geotextile mats[J].Geotextiles and Geomembranes,2010,28(5):422-433.
[ 9 ] SAATHOFF F,OUMERACI H,RESTALL S.Australian and German experiences on the use of geotextile containers[J].Geotextiles and Geomembranes,2007,25(4):251-263.
[10] 赵国权,丁付革.深水域抛填袋装砂筑堤工艺探索[J].中国水运(下半月),2013(9):214-217.(ZHAO Guoquan,DING Fuge.Explore on geotube embankment construction technology in deep water [J].China Water Transport,2013(9):214-217. (in Chinese))
[12] CHU J,YAN S W,LI W.Innovative methods for dike construction:an overview[J].Geotextiles and Geomembranes,2012,30:35-42.
[13] KOFFLER A,CHOURA M,BENDRISS A,et al.Geosynthetics in protection against erosion for river and coastal banks and marine and hydraulic construction[J].Journal of Coastal Conservation,2008,12(1):11-17.
[14] ZHU L J,WANG J Z,CHENG N S,et al.Settling distance and incipient motion of sandbags in open channel flows[J].Journal of Waterway, Port, Coastal, and Ocean Engineering,2004,130(2):98-103.
[15] 应强,张幸农,李伟.沙袋在水流中的沉速、落距[J].泥沙研究,2009(1):15-19.(YING Qiang,ZHANG Xingnong,LI Wei.Settling velocity and distance of sandbags in flows [J].Journal of Sediment Research,2009(1):15-19.(in Chinese))
[16] 杨素勤.水流中土工包沉落模型试验与土工包护岸数值分析[D].南京:河海大学,2007.

