基于PCWR的薄板件装配偏差计算与控制研究
胡朝辉,刘建文
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
汽车市场的竞争日趋激烈,消费者对汽车外观质量、使用寿命和稳定性的要求更加严格,而汽车价格在不断降低,同时产品多样化和新车投放市场的周期呈缩短的趋势。为了适应对质量和功能要求更加严格的市场需求,汽车生产商将汽车产品开发作为抢占汽车市场的重要手段。车身是汽车所有零部件的载体,其质量占整车质量的50%左右,在对汽车其它系统进行变更时,必然涉及到车身结构的变更。为减少汽车开发成本,借鉴现在商品化车型的经验,目前汽车产品开发多为模块化、平台化的设计开发,新车型和现有商品化车型在零部件、生产线及人员上具有共用和继承的关系,处于开发试制阶段的新车型与商品化车型共线生产。降低汽车新产品开发成本的同时也可能由于新车型在设计、制造上的缺陷而导致商品化车型的生产效率降低,甚至造成设备的停工。根据某车企车间反馈的整车制造装配困难和整车质量问题表,车身质量问题导致的装配困难或整车质量不合格问题占整车质量问题的35%以上,其根本原因就是车身尺寸精度不高,需要在试制过程中不断发现问题,提升车身制造和装配精度。车身精度是关系到整车质量和整车装配效率的重要参数,各汽车主机厂将车身装配精度的高低作为汽车新产品能否实施商品化生产的一项重要指标。事实上,在车身设计阶段,车身焊接装配精度提升就纳入到工程师的考虑范围之内,并且形成了一系列装配偏差分析方法和分析软件。
引用格式:
在装配偏差分析方面,形成了极值法、概率法[1]、蒙特卡罗(Monte-Carlo)模拟法等基于刚体假设的装配偏差分析方法,相应的商业软件包括3DCS、VSA、CETOL、TOLMATE等。然而车身零件多为柔性薄板零件,刚度较小,只考虑零件尺寸偏差和零件刚体位移的装配偏差分析不适用于柔性件的装配偏差分析。车身柔性薄板件的装配偏差还与零件结构特征有关,基于柔性件假设的装配偏差分析软件有EVAS、AVA[2],但只限于自用,对于使用者的专业知识背景要求较高,无法通用。因此,基于车身柔性薄板件装配偏差分析,并根据装配体的偏差分析结果对车身零件提出合理建议,从而对车身尺寸偏差进行有效控制,成为提升汽车车身精度,降低开发、制造成本的重要发展方向。
近年来,国内外学者在车身柔性薄板件制造装配偏差计算和偏差控制方面进行了许多有效的研究工作。日本学者Takezawa根据对车身柔性钣金件焊接装配测量数据的分析,认为车身柔性薄板的装配偏差可能小于零件偏差,且接近于刚度较大的零部件偏差[3]。上海交通大学的胡敏对这一现象进行了理论推导和算例验证[4],但未应用于具体的工程实际案例。美国Michigan大学的LIU等建立了一维偏置梁单元模型[5],能够进行简单的一维悬臂梁的焊接装配偏差计算,不能考虑复杂的三维零件的变形。随后HU等提出了偏差流理论[6]和力学偏差仿真模型[7],使用线性假设的装配偏差分析方法,确定了装配偏差与零件偏差的关系。
在上述基于柔性薄板件焊接装配偏差分析计算模型的基础上,可以在设计阶段对车身零件进行焊接装配偏差的模拟,确保零件设计结果具有良好的制造、装配工艺性,能够满足既定的装配精度要求,从而提前对装配偏差进行控制,即通过同步工程实现面向设计的装配偏差控制。在面向设计的装配偏差控制方面,主要进行了工装夹具定位点优化[8-10]、零件焊点位置和数量优化[11]、工艺稳健性优化[2]等。由于柔性薄板件具有易变形的特点,其综合装配偏差不仅与零件尺寸偏差有关,而且与零件本身的结构特性有关,如零件刚度、材料性能等,所以本文提出一种对车身总成的装配偏差分析和结构优化设计的方法,进行柔性薄板件焊接装配偏差的控制。
1 柔性薄板件装配偏差分析
1.1 柔性薄板件焊接装配过程
汽车车身由3~5个层级组成,由300~500个冲压件在100多个主线工位上经流水线焊接装配而成。造成装配偏差的原因较复杂,通常由多个因素累积、耦合和传播,最后形成车体装配偏差。引起车身焊接装配偏差,造成产品质量问题的因素主要有零件设计问题、零件制造质量问题、夹具设计与夹具质量问题和焊接装配操作不当等,点焊热物理过程引起的热变形可以忽略不计[12]。焊装是车体装配主要的连接方式,特别是点焊,可完成90%的车身装配作业[4]。
车身柔性薄板件焊接一般包括定位(Placing)、夹紧(Clamping)、焊接(Welding)和释放(Releasing)四个过程,简称PCWR[13]。零件的定位常常采用六点定位原理,其中“3-2-1”的零件定位方案(即通常所说的一面两销定位)最为常见,如图1所示,三角形表示夹具的定位点和夹紧点,圆形表示定位销。z1、z2、z3共3个定位点约束z向平移、x向转动、y向转动;圆形定位销x1约束x向平移和y向平移;长孔定位销y1约束零件绕z向的转动。由于车身钣金件刚性较差,零件的定位大多采用“N-2-1”的定位方案进行定位和夹紧,由超过3个以上的固定点进行定位,z1、z2、z3为主定位点,z4为过定位点。由于过定位点定位块及钣金件本身的制造误差,在夹具夹紧零件前过定位点与零件本身存在一定的间隙,夹紧后过定位点处的定位块和夹紧块将对零件产生作用力,造成零件焊点位置的变形,零件的位移场在空间上重新分布。
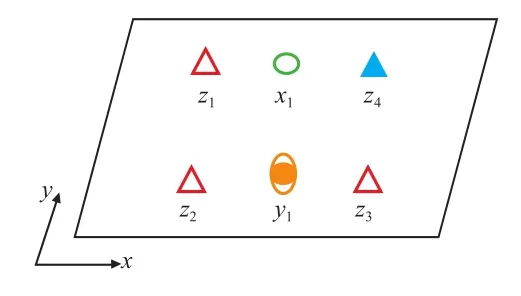
图1 “N-2-1”定位方案
柔性薄板件在焊点位置的制造偏差及其在夹具定位夹紧过程中导致的钣金件在焊点位置的变形,使待焊接装配的两个或多个零件之间存在一定间隙,同时焊枪与钣金件之间也存在一定间隙。焊枪的位置误差也会造成焊枪与零件之间的间隙。焊接装配时,焊枪对零件产生装配力,将消除零件与零件之间、焊枪与零件之间的间隙,并且在零件的关键测点位置产生装配偏差。试验证明,焊接过程中的热效应和焊枪对零件的压力造成零件变薄的趋势对焊接装配偏差影响较小[14]。因此,在焊点位置造成的焊接变形只考虑零件的线性范围内造成的零件偏差,不考虑焊点热变形等非线性因素。
枪焊电极对零件施加夹紧力作用,并接通电源,在零件内部产生焦耳热,零件与零件贴合面电阻最大,温度上升最快,从而形成焊核,完成两个零件的连接。焊接完成后,许多个钣金件连接成一个装配体,而焊枪对装配体的装配力及过定位点处夹具的定位块和夹紧块对装配体的夹紧力仍然存在,且与焊接装配完成之前相同。焊枪及夹紧块释放后,焊枪和夹具的作用力撤消,装配体产生一定的回弹量[15]。
车身装配体的尺寸偏差是上述PCWR焊接过程中逐步叠加积累形成的,车身总成结构的综合装配偏差与零件的制造偏差、夹具制造偏差及焊枪工具的位置偏差有关,还与装配体各零件的结构、材料属性有关。
1.2 焊接装配偏差分析模型
焊接装配过程中存在多种偏差源,偏差源在焊装过程中的传递具有复杂性,基于PCWR过程建立焊接装配偏差模型是进行焊装偏差分析的重要手段。于奎刚[2]、杨阳[10]对两板结构进行的焊接装配偏差分析,胡敏对转向机横梁总成和前围上板总成两件焊接装配的偏差分析[12],均进行了一定的简化。在现有焊接装配偏差模型的研究成果上[2,10,12],以焊装现场实际情况对装配偏差模型进行修正,将修正的焊接装配偏差模型应用于多钣金焊接、多层焊点情况下的装配偏差分析。
在焊装PCWR过程中,零件装配偏差源包含零件制造偏差(“3-2-1”定位基准下测点偏差、焊点偏差、过定位点偏差)、夹具的过定位点制造偏差和焊枪位置偏差。
为了说明柔性薄板件在PCWR过程下产生的装配偏差,给出图2所示的两个零件的装配。在焊接装配之后,零件1、零件2上的关键控制特征点测量点为M1、M2。零件1上的定位点为J11、J12,过定位点为J13;零件2上的定位点为J21、J22,过定位点为J23。W1为焊点,在焊接过程中受到焊枪装配力的作用。

图2 两件焊接的定位点、夹紧点、焊点及测点
(1)零件1的主要定位点为J11和J12,零件安装到夹具上的主要定位点时并未受到任何力的作用,零件1在过定位点J13和焊点W1及测点M1上的偏差分别为{V0b1}、{V0w1}、{V0m1}。同理,零件2安放到夹具上的主要定位点J21、J22时,过定位点、焊点和测点偏差分别为{V0B2}、{V0w2}、{V0m2}。
(2)夹具在J13、J23处的偏差设为{Vf1}和{Vf2},假设夹具夹头的刚度足够大,夹具夹紧后,零件1在J13处的偏移量为{Vf1-V0b1}。测点M1相对于J13偏差的灵敏度矩阵为[Smb1],焊点W1相对于J13偏差的灵敏度矩阵为[Swb1],在W1及M1处的总偏差量分别为{V1w1}和{V1m1},则有:

零件2在W1及M2处的总偏差量分别为{V1w2}和{V2m2},因此:

(3)焊枪对完成定位夹紧的零件进行焊接操作,在W1处分别对零件1和零件2产生装配力{F1}和{F2},从而在M1、M2及W1处产生装配偏差。设焊枪的位置偏差为{Vg},且焊枪的刚度足够大,零件在M1、M2及W1处的总偏差分别为{V2m1}、{V2m2}、{V2w1}、{V2w2}。

式中:[Smw1]和[Smw2]分别为零件测点偏差相对于零件焊点偏差的灵敏度矩阵。
(4)焊接操作过程中,夹具、焊枪夹紧零件1、零件2的作用力为{F1}、{F2}。焊接完成后,夹具及焊枪对装配体的作用力{Fw}为{F1}与{F2}的合力。
即

(5)夹具、焊枪释放,夹紧力撤消,装配体受回弹力{Fk},{Fk}与{Fw}大小相等方向相反。
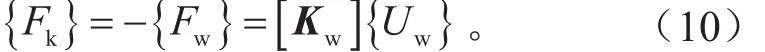
式中:{Uw}为夹具及焊枪释放后各焊点的回弹量;[Kw]为W1处位移相对于W1处施加作用力的刚度矩阵,[Kw]为方阵,且为满秩矩阵。

零件1、零件2在焊点W1处相互作用,造成测点M1、M2产生偏差。

式中:{V3m1}、{V3m2}为零件焊接装配后最终的偏差。
综合式(1)~(14),装配偏差{Vm1}、{Vm2}与各偏差源关系为:

为总灵敏度矩阵,包括刚度矩阵[K1]、[K2]、[Kw],测点相对于偏差源的位移偏差灵敏度矩阵[Smb1]、[Swb1]、[Smw1] 、[Swb2]。
灵敏度矩阵的计算方法如下:如[Smb1]计算,在各个过定位点依次施加单位力的作用,可求得过定位点的刚度,将刚度矩阵的各列向量作为作用力的大小加载到过定位点处,此时过定位点的位移为单位1,测点位置的位移响应即为测点偏差的灵敏度矩阵。
在焊装过程的分工路线设计中,往往由两个以上的冲压件或分总成焊接成更大的车身总成结构,因此为了更加接近复杂的实际情况,需要将上述偏差模型从两钣金的焊接拓展到多个钣金的焊接;焊点连接钣金的层数由两层板拓展到三层板。多层钣金焊接的夹紧力-变形关系方程为:

夹紧力撤消后,零件在夹紧力变形的情况下增加回弹量,表达式为:

多钣金焊接其余的变形方程式参考式(1)~(16)。
1.3 薄板件装配偏差源分布规律
车身薄板件生产纲领一般为单件年产量上万件,部分车型的零件产量达几十万件。随着管理水平和制造水平的不断进步,较少产量的零件采用柔性化生产系统生产,因此不同年产量的零件生产节拍和生产流程相同。对于工艺装备日常磨损、失效等问题进行定期检查和发现,如重保工序的检查周期为4 h,关键工序检查周期为8 h,因此汽车车身零件生产过程稳定,生产质量特征服从正态分布或近似正态分布[16]。
满足正态分布的数据可以用6σ描述其分布范围,如表1所示,根据计算可得68.27%的数据分布在 ±σ范围内;95.45%的数据分布在±2σ范围内;99.73%的数据分布在±3σ范围内[17]。本文以±3σ作为公差的设计值。

表1 不同σ水平每百万零件的缺陷数
以下对某车身分总成零件螺母孔的实际尺寸数据进行测量,测量次数500次,应用Matlab求得螺母孔位置偏差的频率分布直方图,如图3所示。经计算螺母孔位置度尺寸数据的均值为-0.016 7,标准差为0.323 9,显然数据的6σ值为1.943 6 mm,设计要求为±1 mm,即该批零件偏差带宽为1.943 6 mm(满足设计要求)的置信度为99.73%。
装配偏差与各相关偏差源关系的总关系方程式为{Vm1}=[Sm1]{V1},应用蒙特卡罗法,根据偏差源{V1}中各尺寸参数的实际分布特征(正态分布规律)产生的一系列随机数,每个参数的随机数数据规模为500个,均值为0,6倍标准差为偏差源的公差[18]。将随机数误差值代入式(14)和式(15),得出综合装配偏差{Vm1}、{Vm2}的值(各偏差参数均得出500个结果),求综合装配偏差的均值和标准差可得总成结构的装配公差。

图3 座椅安装孔位置偏差的分布直方图
2 焊接装配偏差分析应用
2.1 零件结构及组成
本节将焊接装配偏差分析模型应用于后门槛总成装配偏差的计算,并进行焊接装配偏差分析模型的验证。后门槛总成是下车体的组成部分,首先在分装线上由四部分钣金拼装成后门槛总成,然后在白车身整车焊接的主线上将后门槛焊接到下车体的车架上。门槛总成由前连接板1、踏板2、支承板3及下导轨4组成,零件1、2、3两两之间均有焊点连接,如图4所示。由于焊点连接的钣金层数不同,夹紧力-回弹量的方程式不同,首先对零件之间的焊点进行分组,焊点组号及连接的零件见表2 ,其中z组焊点涉及三层板焊接。

图4 门槛总成零件

表2 焊点分组
总成结构的测点偏差包括间隙、面差、孔的位置度偏差,从总成GD&T图和测量工艺卡中选取零件1及零件2上的部分测点进行装配偏差的计算,分别为零件1上测点M11、M12、M13相对理论值的面差及零件2上安装孔M21相对于理论值的位置度偏差M21x(x向)、M21y(y向),如图5所示。首先进行零件偏差源及门槛总成装配偏差的实际数据测量,使用面差表测量型面面差,使用划线销及直尺测量安装孔位置度偏差。对偏差源的数据测量项目包括零件在测点位置、焊点位置和过定位点位置的冲压制造偏差。

图5 左后门槛总成测点
根据式(1)~(9)可知,综合装配偏差的偏差源除了与零件偏差有关,还与工装夹具和焊枪偏差有关。使用三坐标测量机对夹具定位点、夹紧点及定位销的位置度偏差进行测量,经测量夹具及焊枪位置度偏差的设计值和实际测量值在±0.1 mm范围内,相对零件尺寸偏差较小,在仿真计算时忽略不计。
零件定位按前述方案,包含确定性定位点及过定位点,过定位点数量及编号见表3。

表3 零件过定位点
2.2 刚度矩阵和灵敏度矩阵计算
对零件1进行刚度矩阵计算,约束件1确定性定位点,在焊点1位置施加单位力[10],求得件1上9个焊点及LP11~LP14位置的位置响应为:

计算前规定面差的正方向,式中负号表示变形方向与规定的面差正方向相反,同理可在其余焊点及过定位点分别施加单位载荷,将各响应向量组成零件的位移响应矩阵[C],刚度矩阵为[K]=[C]-1111(表4)。本例中,刚度矩阵其余刚度矩阵[K2]、[K3]、[Kw]的计算方法相同。

表4 零件1焊点及过定位点刚度矩阵[K1]13x13
焊点相对于夹紧点偏差的灵敏度矩阵[Swb1]的计算,首先在过定位点LP11~LP14各处依次施加单位力,求得LP11~LP14处单位力响应向量分别为:{Cb11}、{Cb12}、{Cb13}、{Cb14},组成过定位点的单位力位移响应矩阵为:

零件1过定位点的刚度矩阵[Kb1]=[Cb1]-1,将[Kb1]各列向量作为载荷分别加载到LP11、LP12、LP13、LP14各点,此时LP11、LP12、LP13、LP14各点的位移分别为1 mm,得各焊点关于LP11~LP14的单位位移响应分别为[Sw11]、[Sw12]、[Sw13]、[Sw14],将单位位移响应的向量组合成灵敏度矩阵:

按该方法可得其余灵敏度矩阵[Smb1]、[Smw1]、[Swb2]、[Smb2]、[Smw2]、[Swb3],将刚度矩阵及偏差灵敏度矩阵代入式(1)~(18),式(17)和式(18)中偏差源向量{V1}、{V2}按测量值的偏差范围使用蒙特卡罗法产生随机数进行模拟,得出装配偏差结果见表5(装配偏差源数据除夹具及焊枪偏差在±0.1 mm范围内忽略不计外,其余均考虑)。结果表明,计算仿真的车身总成结构综合装配偏差结果与实际大致符合,计算模型与实际零件偏差源和焊接装配偏差有较好的一致性。
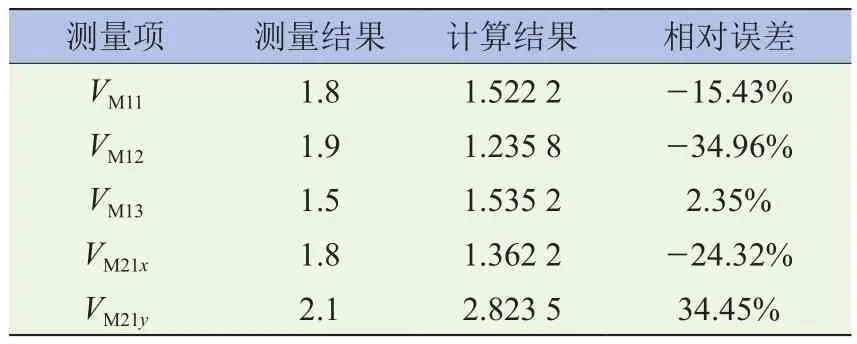
表5 门槛总成装配偏差测量及计算结果
3 基于装配偏差分析的零件特征优化
3.1 零件结构特征及公差优化方法
以偏差分析为基础进行装配偏差控制,目前面向设计的装配偏差控制方法主要进行工艺方面的优化,以下探讨对零件结构的优化达到最低成本控制装配偏差目的的方法和流程。
零件冲压制造的缺陷包括开裂、起皱、回弹,主要引起零件尺寸偏差的缺陷是冲压件回弹,且在保证相同的零件制造精度条件下,不同结构的零件难易程度不同,因此引入公差-成本的关系模型。本研究使用公差-成本反比关系模型,表达式为:

式中:ki为成本系数;Ti为零件制造公差,i=1, 2, 3…,n。
对零件特征进行优化设计,要求零件的冲压制造成本最小化,总成结构的综合装配偏差在设计规定的范围内(装配公差带宽小于2 mm)。设计变量为零件制造公差Ti、矩阵[K1]的元素Kij。优化设计函数表述为:式中:总偏差灵敏度矩阵[S]为刚度矩阵[K1]的函数;装偏差源{Vi}根据零件设计公差带宽{Ti}通过蒙特卡罗法产生随机数得出,是{Ti}的函数,详细优化过程如图6所示。


图6 基于零件优化设计的装配偏差控制
本节对门槛总成进行零件结构特征参数及零件制造公差的优化设计,取成本系数k1=1 000,k2=5 000,k3=3 000,k4=2 000(k1、k2、k3、k4分别为零件1、2、3、4的成本系数,假设同一零件所有位置的冲压精度成本系数相同)。使用遗传算法对零件1的刚度矩阵及各偏差源的公差进行优化计算,根据目标变量编写适应度函数,设计变量数为246(其中包括矩阵元素数量169、装配偏差源数量77),使用带罚函数的优化标函数进行约束条件的定义。初始种群为20,为减少优化迭代次数,设置优化变量初始种群范围(遗传算法系统默认初始种群为0~1),零件偏差源的初始种群范围为1.5 mm~2.5 mm,刚度矩阵各元素的初始种群定义在原刚度基础上±5 N/mm的范围内。迭代计算300次后得出优化后的刚度矩阵[K1](表6)及零件公差(表7)。由优化前后成本比较可知,通过零件结构优化进行装配偏差控制的方法降低成本效果明显。
将优化前后的刚度矩阵进行比较,当零件结构的刚度满足优化后的刚度矩阵时,为控制装配偏差需要使用的成本最低,零件1刚度矩阵各点刚度变
3.2 零件结构特征及公差优化应用
化量见表8。然而确定的车身结构能够求解出唯一确定的刚度矩阵[19],零件刚度和灵敏度矩阵各元素却无法与零件结构形成一对一的映射关系,即当刚度矩阵和灵敏度矩阵确定时,无法找到唯一的零件结构与之对应,因此需要借助工程师的实际经验和不断的数据积累获得零件结构与各相关矩阵的关系,通过各点刚度变化量确定零件结构的刚度是否需要增加(或减少)。常见的增加(减少)零件刚度的方法有增加(减少)零件厚度尺寸、设置加强筋增加零件刚度和结构特征尺寸变更等。

表6 零件1焊点及过定位点刚度矩阵[K1]13x13优化结果

表7 零件偏差源优化结果

表8 刚度矩阵变化量[ΔK1] 13x13
4 结论与展望
(1)刚体装配偏差理论难以适用于车身柔性薄板件装配偏差分析,基于PCWR过程及自由回弹理论建立柔性薄板件装配偏差模型,能够预测零件结构的装配偏差。
(2)研究表明:装配偏差与零件制造偏差有关,还与零件结构所确定的零件刚度矩阵及灵敏度矩阵有关。通过优化设计,将灵敏度大的偏差源转移到少数几个主要零件上来,从而实现控制少数几个零件的精度达到控制整个车身分总成结构精度的目的。本文提出的装配偏差分析及优化方法能够帮助设计工程师和工艺工程师进行设计和零件优化变更。
(3)在进行装配偏差计算时,借助现有的有限元分析软件进行零件和总成的刚度矩阵及灵敏度矩阵各元素的求解,计算效率较低。目前常用的装配偏差分析软件大多基于刚体假设,基于变形体假设的装配偏差分析软件较少或限于开发者自用,因此亟待开发一种商业化的柔性件装配偏差分析软件。
(4)车身钣金件优化设计结果为设计者提供了结构优化的指导性建议,在刚度矩阵与零件结构之间建立确定性的对应关系还需要不断进行数据和经验的积累。
参考文献(References):
[1]杨沿平.机械精度设计与检测技术基础[M].北京:机械工业出版社,2013:173-179.YANG Yanping. Design of Mechanical Precision and Detection Technology Foundation[M].Beijing:China Machine Press,2013:173-179.(in Chinese)
[2]于奎刚. 车身柔性薄板产品装配建模及工艺稳健设计研究[D]. 上海:上海交通大学,2010:64-67.YU Kuigang. Assembly Modeling and Robust Technology Design Research of Automotive Body Compliant Sheet Metal Products[D]. Shanghai:Shanghai Jiaotong University,2010:64-67. (in Chinese)
[3]TAKEZAWA N. An Improved Method for Establishing the Process Wise Quality Standard[J]. Reports of Statistical and Applied Research,JUSE,1980,27(3):63-76.
[4]胡敏,来新民,林忠钦,等. 车体多柔性件装配的误差分析[J]. 上海交通大学学报,2000,34(10):1365-1368.HU Min,LAI Xinmin,LIN Zhongqin,et al. Variation Analysis for Multi-flexible Autobody Assembly [J].Journal of Shanghai Jiaotong University,2000,34(10):1365-1368. (in Chinese)
[5]LIU S C,HU S J. An Offset Finite Element Model and Its Applications in Predicting Sheet Metal Assembly Variation[J]. International Journal of Machine Tools &Manufacture,1995,35(11):1545-1557.
[6]HU S J,KOREN Y. Stream-of-Variation Theory for Automotive Body Assembly[J]. CIRP Annals-Manufacturing Technology,1997,46(1):1-6.
[7]LIU S C,LEE H W,HU S J. Variation Simulation for Deformable Sheet Metal Assemblies Using Mechanistic Models[J].Transactions of NAMRZ/SME,1995,23(5):235-240.
[8]姜潮,韩旭,钟志华. 电阻点焊焊装夹具定位点的优化设计[J]. 机械工程学报,2009,45(4):192-196.JIANG Chao,HAN Xu,ZHONG Zhihua. Locator Optimum for Resistance-Spot-Welding Fixtures[J]. Journal of Mechanical Engineering,2009,45(4):192-196.(in Chinese)
[9]邓乾旺,刘勇. 基于影响系数法的薄板电阻点焊定位点优化[J]. 机械科学与技术,2014,33(7):996-999.DENG Qianwang,LIU Yong. Optimal Fixture Layout of Sheet Metal Resistance Spot-Welding Based on In fl uence Coef fi cient Method [J]. Mechanical Science and Technology for Aerospace Engineering,2014,33(7):996-999. (in Chinese)
[10]杨阳.柔性薄板件装配偏差分析[D]. 杭州:浙江大学,2014:67-74.YANG Yang. The Assembly Deviation Analysis of Flexible Thin Pieces[D]. Hangzhou:Zhejiang University,2014:67-74. (in Chinese)
[11]马强. 车身柔性薄板焊点布置优化技术研究[D].长春:吉林大学,2016:52-54.MA Qiang. Research on Layout Optimization of Welding Spot for Automobile Sheet Metal Assemble [D]. Changchun:Jilin University,2016:52-54.(in Chinese)
[12]胡敏. 车身点焊装配偏差分析的建模方法研究[D].上海:上海交通大学,2000:7-8.HU Min. Study on Welding Variation Modeling in Auto-Body Assembly [D]. Shanghai:Shanghai Jiaotong University,2000:7-8.(in Chinese)
[13]文文. 车身薄板件装配误差控制方法研究[D]. 长沙:湖南大学,2012:13-15.WEN Wen. Research on Assembly Deviation Control Method of Body Sheet Metal [D]. Changsha:Hunan University,2012:13-15.(in Chinese)
[14]CAI W,WANG P C,YANG W. Assembly Dimensional Predication for Self-piercing Riveted Aluminum Panels[J].International Journal of Machine Tools and Manufacture,2005,45(6):695-704.
[15]HUANG Wenzhen. Methodologies for Modeling and Analysis of Stream-of-Variation in Compliant and Rigid Assemblies[D]. Wisconsin:University of Wisconsin Madison,2004:24-25.
[16]姬舒平,孙贤会,马玉林. 一种基于制造环境的统计公差分析方法[J]. 中国机械工程,1999,10(3):249-252.JI Shuping,SUN Xianhui,MA Yulin. A Statistical Tolerance Analysis Method Based on Manufacturing Environment [J]. China Mechanical Engineering,1999,10 (3):249-252.(in Chinese)
[17]孙光永,李光耀, 陈涛,等. 基于6σ的稳健优化设计在薄板冲压成形中的应用[J].机械工程学报,2008,44(11):248-254.SUN Guangyong,LI Guangyao,CHEN Tao,et al.Sheet Metal Forming Based 6 Sigma Robust Optimization Design[J]. Chinese Journal of Mechanical Engineering,2008, 44 (11):248-254.(in Chinese)
[18]邓乾旺,文文. 基于拉丁超立方抽样的薄板装配误差分析[J]. 中国机械工程,2012,23(8):947-951.DENG Qianwang,WEN Wen. Sheet Metal Assembly Deviation Analysis Based on Latin Hypercube Sampling[J].China Mechanical Engineering,2012,23 (8):947-951.(in Chinese)
[19]谭继锦. 汽车有限元法[M]. 北京:清华大学出版社,2012:20-25.TAN Jijin. Finite Element Method of Automobile [M].Beijing:Tsinghua University Press,2012:20-25.(in Chinese)

