模型法在中学物理解题中的应用

本文对模型法在高中物理解题中的应用进行了深入的剖析，简要介绍了模型法的分类和求解流程，将模型法分为实体模型、过程模型及问题模型，并分别举例进行了说明。模型法能够帮助我们抓住问题的本质，忽略次要干扰信息，将实际问题理想化。模型法的应用能够提升我们对物理问题的分析和求解能力。

物理学是研究物质相互作用规律及其基本结构的科学，关于高中物理解题方法方面，已有大量文献进行了深入研究，如实验法、模型法、推理法等等，而模型法在物理解题的物理规律构建和概念的形成中有着凸出的贡献。其中模型法在形成物理概念、建立物理规律中起着重要作用。模型法是我们在求解物理问题过程中，通过对问题模型的建立，帮助我们抓住问题的核心和重点，忽略题中的干扰信息，在头脑中形成一个清晰的思路。更进一步讲即是通过模型把物理问题实际化。模型法应用于高中物理解题中，能够极大地帮助我们对复杂物理知识及问题的分析和求解能力。

模型法在物理求解中的应用

模型法求解物理问题的流程

用模型法解决物理问题的基本程序如下：

1）审题，首先将物理问题中的文字映射到大脑中，形成一个初步的求解思路，并将题中所要表达的物理场景利用示意图展示出来。

2）分析，利用模型法的方式，提炼出物理问题中的本质信息，忽略掉次要的干扰信息，从而形成清晰的解题思路。首先对题中所要表达的物理场景进行分析，从主要特点中分析出物体的运动特点如匀速圆周运动等，在大脑中搜索比对学过的物理模型，从而建立该物体的运动模型进行求解，这样能够帮助学生清晰的分析和求解问题。

3）再现，回忆模型所遵循的所有物理规律，使学生真正清楚模型的物理意义。

4）决策，结合题中已知信息，找出有关该问题的全部求解方案，再根据已知条件和目标之间存在的一系列关系和物体运动过程所遵循的物理规律，选择出最好的解决方法。

5）运算以及讨论，运算即是运用相关的物理规律进行求解或者进行逻辑推理得出结果，在求解完成后，需要对结果的合理性方面进行讨论，主要就是结合题意利用物理规律对题中的实际问题进行分析。

模型的分类与模型法的应用举例

模型法能够准确的抓住问题的本质，忽略其他次要的干扰信息，帮助我们准确的分析和处理问题，提升我们对复杂物理问题的求解和处理能力。我们所遇到的模型，一般可分为下面几种情况：

1）实体模型。

实体模型是对物理对象进行理想化处理后建立的模型，常用于建立某个物理概念，能够提升我们对物理概念的理解能力。如质点、理想气体、弹簧振子、原子核式结构、点电荷等，再比如对连续物质之间的相互作用进行研究时，通常需要建立截面模型或圆柱体模型、分子（原子）的立方体或球体模型等。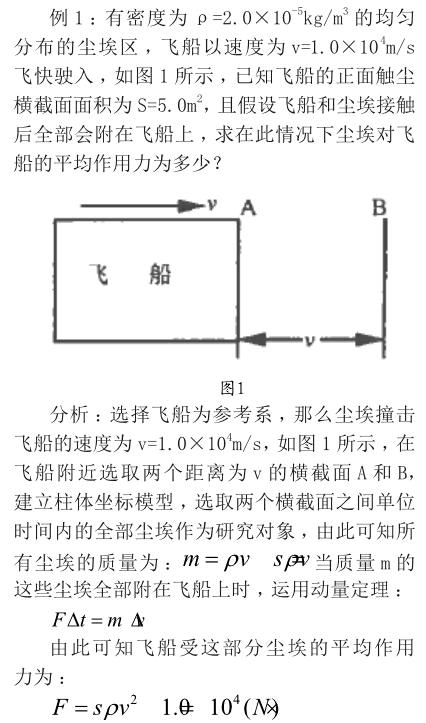

例2：电流微观模型的建立与应用：有一导体AD示于图2，在其两端加上一定数量的电压，设导体内自由电荷电量与沿着导体定向移动的速度分别为q和v；导体的横截面积为S且每单位体积内所含的自由负荷数量为n，在导体中选取距离为数量为v的横截面B和C，要求求解出两个面之间的负荷电量（单位时间内）是多少？

2）过程模型。过程模型通常将物体运动过程理想化，不考虑其他干扰信息。如研究自由落体时，为了简化问题，常常忽略掉空气阻力对物体运动的影响，将运动过程理想化为运算或者匀变速的直线运动。这样的模型还有弹性碰撞、匀速圆周运动、平抛运动等。

例3：天文學家研究发现，银河系中心可能存在一个大“黑洞”，黑洞是宇宙中最奇特和神秘的天体，是超强引力源，黑洞会吸住靠近它的全部物质，距“黑洞”60亿千米的星体围着黑洞旋转，速度达到200m/s，即便是光子这种速度为光速也不能反射，设已知万有引力常量G=6.67×10-11N m2/kg2，要求求解“黑洞”的质量和最大半径是多少？

分析：结合题中信息，（1）距离黑洞60亿千米的星体围绕黑洞做的是圆周运动；（2）即使光子这样速度为光速，也会被黑洞吸住不能反射。所以首先应该建立形体饶黑洞的圆周运动模型，求出黑洞的质量，然后根据第二点信息，将星体代替为光子，求出黑洞的最大半径。

解：（1）设质量分别为M、m的 “黑洞”和星体之间的距离为r，由：

3）问题模型。对物理问题进行分析时，选择的分析角度不一样，就会导致最终建立的模型也不一样。这种模型在实际应用中得到广泛应用，如“导体切割磁感线产生感应电动势”“碰撞”等这类模型。

例4：“导体切割磁感线”的问题模型：某处存在一个均匀分布的电磁场，磁感应强度为B，示于图3，将单匝矩形线框abcd以垂直于磁感应线的方向置于该匀强磁场中，ab为线框可动部分，现让ab在时间Δt内向右运动到a1b1处，速度为v，设ab的长度为L。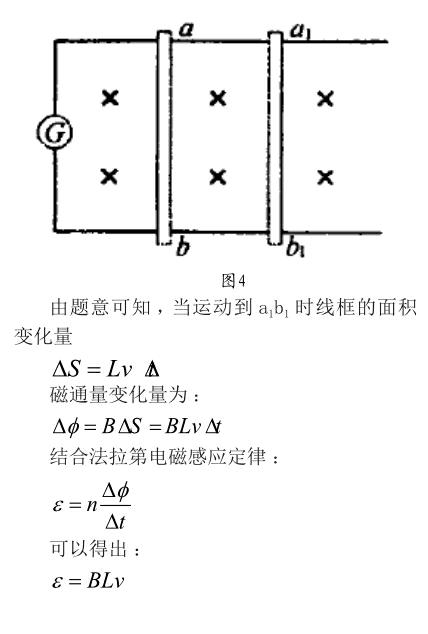

结论

综上所述，我们可以知道模型法在中学物理解题中意义重大，模型法能够将实际问题理想化，帮助我们抓住复杂问题的本质，忽略次要干扰信息，能够极大地提高我们对复杂物理知识及问题的分析和求解能力。

参考文献

[1]杨生强.物理模型在高中物理解题中的应用[J].数理化解题研究，2016（18）.

[2]李境祎.物理模型在高中物理解题中的作用探讨[J].数理化解题研究，2016（31）：64.

[3]刘熠，胡梦姣.例析中学物理解题中的构建理想模型法[J].数理化学习（高中版），2008（1）：26-30.

[4]赵小峰.物理模型在解题中的应用[J].中学物理，2011，29（13）：58-59.

[5]施晓红.模型法在中学物理解题中的应用[J].兰州文理学院学报（自然科学版），2005，19（4）：83-86.

[6]刘晓琳.例析高中物理解题中的理想模型法[J].中学生数理化（学研版），2017（2）：66.

（作者简介：周渝杰，绵阳中学实验学校。）endprint