基于有限元的矩形薄壁板件受力特性研究

矩形薄壁板件结构的受力是工程、机械、航空航天等多领域中都会涉及到的基础力学分析问题，矩形薄壁板件悬臂梁是等截面结构中的一种，从理论计算和有限元分析两个角度，可以很好地研究工程中等截面梁受力分析的方法及受力特性的规律。

在实际工程中遇到的复杂的结构或结构可以结合有限元模型离散单元，计算机硬件技术的快速发展和新的数值算法不断出现，大型复杂问题的有限元分析已成为工程技术领域的常规工作。ANSYS软件被广泛应用于计算机辅助工程，是最强大的有限元分析软件。ANSYS和有限元分析作为工程问题解决的重要手段之一，必将成为各领域科学研究和产品开发的支柱。

矩形等截面薄壁板件悬臂梁简介

矩形等截面薄壁板件悬臂梁在懸臂梁问题中是一种经典情况，我们可以通过理论计算得到其挠度和弯曲正应力求解公式，代入数值后可得到正确的解析解。然后对矩形等截面薄壁板件悬臂梁进行有限元分析，得到仿真解，用解析解对比仿真解，寻求最小误差，找到正确的有限元分析方法。

矩形等截面薄壁板件悬臂梁的弯曲正应力和挠度的理论求解

矩形等截面薄板悬臂梁的弯曲正应力求解

矩形薄板悬臂梁受力弯曲时横截面上同时存在弯曲正应力和弯曲切应力，设矩形薄板悬臂梁的长度为l，板一端受集中载荷为F，截面高为h，薄板截面宽为b。如图1所示。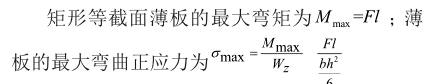

矩形等截面薄板悬臂梁的挠度求解公式

矩形等截面薄板悬臂梁的有限元分析

将矩形截面悬臂梁的有限元分析分为两方面：第一，这个物理模型的预处理，包括矩形等截面薄板悬臂梁建模，虚拟梁网格的划分，最后加载和求解。第二，悬臂梁模型的后处理，包括浏览分析结果、受力变形情况、应变和应力产生的效果等。

矩形等截面薄板悬臂梁有限元分析的前处理

选择单元类型

选择ANSYS188单元进行矩形等截面薄板悬臂梁的建模，因为ANSYS BEAM188适用于三维线性梁的分析。KEYOPT（1）可以控制BEAM188在每个节点上的自由度。当KEYOPT（1）=0时，BEAM188上有6个自由度。分别是沿X轴，Y轴，Z轴的位移和绕其的转动。当KEYOPT（1）=1时，就会增加第七个自由度，也就是翘曲量。

该元素可应用于线性、大挠度和非线性应力。它包含应力刚度，默认情况下由NLGEOM在一些分析中打开。应力刚度应在弯曲、横向弯曲和扭转稳定性分析中打开。弹性、蠕变和塑性模型都是允许的（不考虑分段形状）。

定义材料参数

在ANSYS中定义矩形等截面薄壁板件悬臂梁材料参数的操作步骤：ANSYS主菜单：预处理→材料→模型→结构→线性→弹性→材料各向同性，在ANSYS 主菜单中的Preprocessor的材料属性（Material Models）设置对话框中，依次选取结构、线性、弹性、各向同性，在此将悬臂矩形薄壁板件的弹性模量设定为1E10，泊松比设定为0.25。

定义截面参数

在ANSYS主菜单中预处理（Preprocessor）里的截面属性栏里选择Beam（梁），在Common Sections中定义矩形等截面薄板悬臂梁的截面参数。由于是等截面梁，所以我们只需定义一个截面参数。

构造Modeling

在这种情况下，模型是由自下而上的方法构造的，该方法是将最低图对象的对象建立到最高图元对象的对象，即先建立点，然后将点连起来。通过ANSYS Main Menu里的预处理（Preprocessor）选择建模（Modeling）来创建关键1（0，0，0），关键点2（16，0，0），并通过ANSYS Main Menu里的预处理（Preprocessor）选择建模（Modeling）里的In Active Coord连接1、2关键点生成线段。

网格的划分

已经设定好了矩形等截面薄板悬臂梁的材料特性后，需要主要定义网格的大小、形状，然后将网格进行划分。

对已矩形等截面薄板悬臂梁的网格划分操作步骤：通过ANSYS Main Menu里的预处理（Preprocessor）选择建模（Modeling），用 Size Cntrls 里ManualSize的线段选择所有关线段Element Sizes on All Selected Lines，设置 NDIV为0.1，最后确定。

Loads

对矩形等截面薄板悬臂梁端施加约束，主要通过ANSYS主菜单里的预处理（Preprocessor）选择Loads来定义加载参数和加载的关键点，例如在这儿对关键点1点所有方向上的位移施加约束，选择Min，Max，Inc： 1 → OK → lab2：ALL DOF（）。

加载

最后，在关键点2上施加需要的–Y方向的载荷，和施加约束的前端界面选择一样，但是需要在Apply中选择Structural 然后选择Force/Moment，最后对关键点2也就是Min，Max，Inc： 2，施加力的方向选择FY，力的大小为-1 000N，最后确认OK。

计算分析

所有的模型建立好以后，查验参数设置的正确性，就可以开始计算机处理，用到ANSYS主菜单里的Solution，选择Solve里的Current LS，并确认，等待分析结果。endprint

矩形等截面薄板悬臂梁有限元分析的后处理

在矩形等截面薄板悬臂梁建模分析中，采用了POST1，对模型计算结果的求解步骤，包括位移（变形）、应变和应力进行了详细的分析。解决方案完成后，将在POST1中出现Plot Results menu选项，该选项将选择矩形等截面薄壁板变形、位移和应力变化。通过Plot Results，选择变形的形状中的Def + undeformed可以查看矩形等截面薄壁板件的变形，查看矩形等截面薄壁板件各处的应力大小Contour Plot → Nodal Solu → Stress， Von Mises， Undisplaced shape key，如图2所示。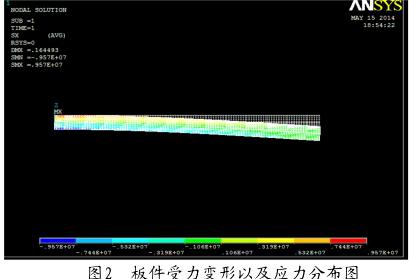

图2中左上角记录了最大挠度，最大弯曲正应力以及最小弯曲正应力。

得到矩形等截面薄壁板件仿真解，最大挠度为0.164 493，最大弯曲正应力为9.57E+06。

解析解与仿真解结果对比

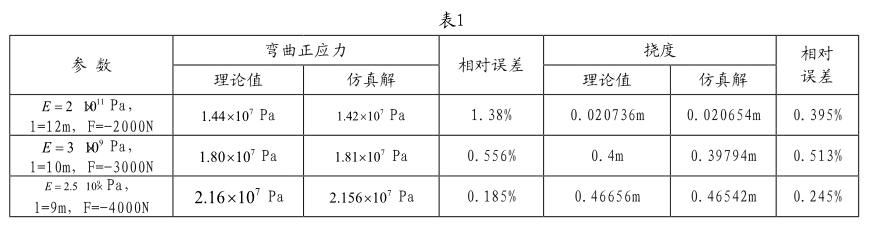
多組数据分析验证结论如表1所示。

由表1可看出各项数据相对误差基乎为零，得出解析解和仿真解是一致的结论，所以以上对悬臂矩形薄壁板件结构的建模、有限元分析和求解的方法是正确的。从而，我们可以用这种有限元分析方法，验证类似的结构受力问题。在推导悬臂等腰梯形薄壁板件结构挠度计算的一般公式后，就可以用相同的仿真建模以及有限元分析方法，求解出仿真解，来验证解析解，从而证明推导出的挠度一般公式的正确性。

参考文献

[1]张红松，胡仁喜.ANSYS13.0有限元分析从入门到精通[M].北京：机械工业出版社，2012.

[2]王勖成.有限单元法[M].北京：清华大学出版社，2003.

[3]秦飞.材料力学[M].北京：科学出版社，2012.

[4]单祖辉.材料力学教程[M].北京：高等教育出版社，2004.

（作者简介：赵晨迪，助理工程师，中国民航飞行学院飞机修理厂，研究方向为航空活塞发动机维修及结构强度分析。）endprint