基于多策略SSO 和改进A*算法的无人机动态航迹规划

田 阔, 刘 旭

(中国飞行试验研究院，西安 710089)

基于多策略SSO 和改进A*算法的无人机动态航迹规划

田 阔, 刘 旭

(中国飞行试验研究院，西安 710089)

针对无人机遇到突发威胁动态航迹规划问题，提出了一种基于多策略SSO和改进A*算法的无人机动态航迹规划方法。该方法将无人机航迹规划划分为静态航迹规划和突发威胁实时规避两个阶段:首先，对于静态航迹规划阶段，采用多策略SSO优化算法对极坐标航迹规划模型进行求解，通过引入完全弹性碰撞、自适应跳跃等机制，在有效满足飞行性能约束的同时，提高了航迹规划结果的可行性;其次，对于突发威胁实时规避阶段，采用改进A*算法对局部区域进行航迹重规划，通过拓展A*算法搜索邻域个数和引入最小“弯折”估计代价函数，在保证实时性要求的同时，能够规划出更加平滑的最优航迹。仿真结果表明，提出的方法能够有效地给出更为满意的无人机动态航迹规划路线。

航迹规划； 无人机； 群居蜘蛛优化； 改进A*算法

0 引言

近年来，随着无人机(UAV)技术的迅猛发展，其在救援搜索、精确打击、追踪侦察、低空突防等领域得到了越来越多的应用[1]。但从实战角度来看，无人机在航迹规划、信息交换、协同配合等方面还有很多难关需要突破[2]。特别地，无人机航迹规划作为实现UAV自主控制的重要环节[3]，吸引了学者们的广泛关注。

无人机航迹规划是指在综合考虑外部环境因素和自身飞行性能的基础上，为UAV规划出从起飞点到目标点且满足各种约束条件的最优可行航路[4-5]。PRM,A*算法,人工势场以及智能优化算法等是目前应用较为广泛的航迹规划算法。文献[5]提出了一种基于网格概率地图法的快速航迹规划算法，在高效实现航迹规划的同时有效满足了实际飞行需求，但是该算法无法保证得到较优航迹；文献[6]针对航迹规划实时性问题，设计了一种基于RRT的实时航迹规划算法，仿真实验也证明了该算法的有效性，但是算法需要实时更新外部环境等信息，导致算法计算量相对较大；文献[7]在A*算法的基础上设计了一种分级规划策略航迹规划算法，通过初始规划和精细规划，可以得到最终的多条可行航迹，但是该算法以网格顶点为搜索领域，使得航迹“弯折”较多，导致航迹可飞行性降低；文献[8-9]通过将进化算法、蚁群优化等智能优化算法应用于航迹规划，进而能够得到最优航迹，但是智能算法易于陷入局部最优,仍是亟需解决的问题。研究表明UAV航迹规划是一个NP-Hard难题，并且实际战场三维航迹规划可以转化为多个二维平面航迹规划[10]，因此研究二维突发威胁动态航迹规划具有重要意义。

为此，本文提出一种基于多策略SSO(Multi-Strategy Social Spider Optimization,MSSSO)[11]和改进A*算法的无人机动态航迹规划算法：利用多策略SSO对航迹规划模型进行求解，得到静态最优航迹，并在此基础上采用改进A*算法对突发威胁区域进行局部航迹再规划。该算法通过引入完全弹性碰撞、自适应跳跃机制、最小“弯折”估计代价函数以及拓展A*算法搜索邻域个数，从而得到满足飞行性能约束、有效规避突发威胁和航迹代价最小的可行飞行航迹。

1 航迹规划建模

二维平面无人机航迹规划具有典型研究意义，这不仅是因为可以将三维空间航迹规划转为水平和垂直剖面进行分析[2,5,10]，而且在实际应用环境中，通常为无人机设定最小安全曲面，即无人机以一定高度进行飞行。无人机航迹规划的目的是寻找一条能够满足各种飞行约束条件，并且有效规避各种威胁的航程P{S,X1,X2,…,Xm,T}，其中,S,T分别为航迹起点和目标点，Xi(i=1,…,m)为航迹节点。

定义1定义航迹节点Xi为多维向量，即

(1)

式中：Peri，Thri，Fli分别表示无人机性能约束条件(Lmax，Lmin，Rmin，Hsafe分别为最大航程、最小航程、最小拐弯半径和最低飞行高度);无人机威胁约束(pr，pm，pg，pa，pe分别为雷达威胁、导弹威胁、高炮威胁、大气威胁和地形威胁)和无人机状态信息((xi,yi);Hi，Oi，Ri，vi分别为无人机当前位置、高度、油耗、曲率半径和飞行速度信息)。

定义2定义无人机航迹规划模型为航迹综合代价最低，即

(2)

∑f(s)=ωOfO+ωHfH+ωrfr+ωmfm+
ωgfg+ωafa+ωefe

(3)

式中,fO，fH，fr，fm，fg，fa和fe分别表示油耗代价、高度代价、雷达威胁代价、导弹威胁代价、高炮威胁代价、大气威胁代价和地形威胁代价。

威胁代价计算如下。由于油耗代价和高度代价分别与航程及飞行高度成正比，因此有

(4)

式中：c1，c2为比例系数；hi为第i段航程高度。对于fr，fm，fg，fa和fe，由于这些威胁与无人机和威胁中心的距离有关，因此可以将第j(j=1,2,…,m+1)段航程均分为n段(如图1a所示)，并取n+1个分段端点威胁平均值作为该段航程威胁代价，即K个同类威胁对第j段航程威胁代价fK,j为

(5)

式中：fk,j为威胁k对第j段航程的威胁代价；p(dk,Xi)为威胁k对航迹点Xi的威胁。根据式(5)可以得到威胁K对整个航迹的威胁代价fK(K∈{r,m,g,a,e})，即

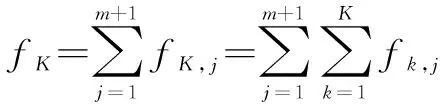
(6)

2 静态航迹规划实现

2.1 极坐标空间处理

对于无人机静态航迹规划问题，外部飞行环境能够事先获取，并且无人机在飞前就已经完成了静态航迹规划，因此航迹规划模型求解精度成了问题关键，本文采用群居蜘蛛优化算法(SSO)对航迹规划模型进行求解。为了使得SSO更好应用于无人机航迹规划过程，对二维空间进行极坐标处理(如图1b所示)：将S与T之间距离进行M等分，每个分段长度为ρ(合理设定M取值，可以使无人机满足最小航程约束)。对于航迹节点Xi，设其极坐标角度为θi，则Xi位置信息描述为(iρ,θi)。设直线ST与水平直角坐标系x轴夹角为α，根据坐标转换公式，可以得到(xi,yi)与(iρ,θi)对应关系，即

(7)

(8)

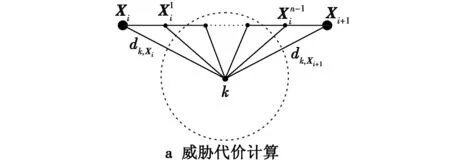
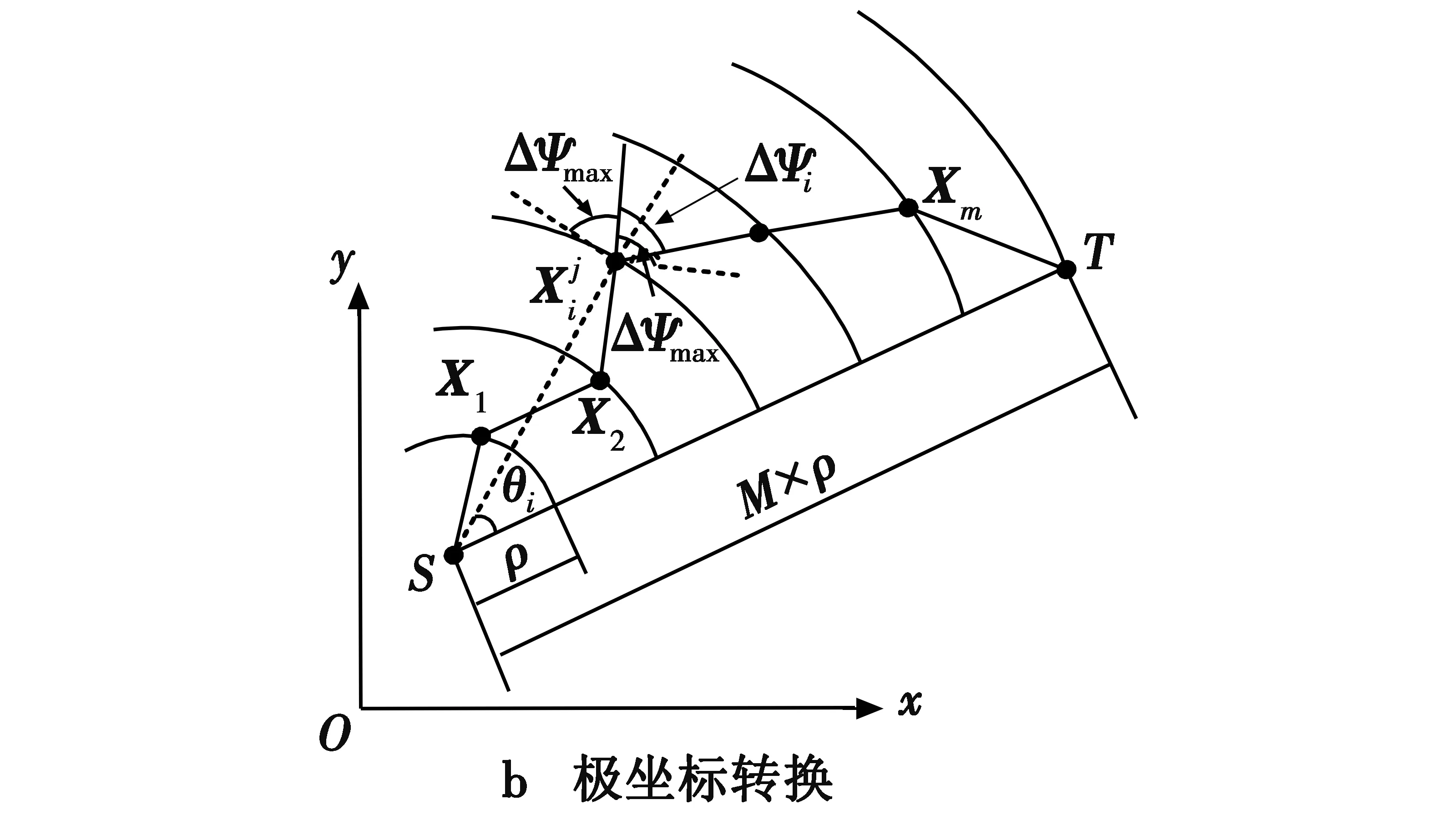
图1 威胁代价计算与极坐标转换Fig.1 Threat cost calculation and polar transformation

2.2 多策略SSO优化算法

研究表明，智能优化算法在处理NP-Hard问题时表现出突出优势，并在实际工程领域中得到了广泛应用[12]，本文以最近才被提出的SSO算法为基本群体，并引入“完全弹性碰撞”、自适应跳跃机制以改变多策略SSO优化算法全局寻优能力(SSO基本原理参考有关文献，不再赘述)。

2.2.1 完全弹性碰撞

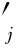
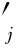
(9)

从式(9)可以看出，新的个体融合了自身历史最优个体和当前种群最优个体信息，体现了学习融合，因此采用b′(t)对Sj(t)进行更新，更新公式为

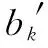
(10)

σjk(t)=|bk(t)-gjk(t)|

(11)

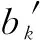
定义3t时刻，对于具有F个种群个体且采用完全弹性碰撞更新策略的蜘蛛种群，其种群样本离散度MDt(F)定义为

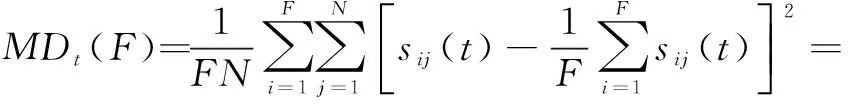
(12)

从式(12)可以看出，MDt(F)反映了种群个体距离样本中心的离散程度，取值越大，表明种群多样性越高。

推论2种群样本离散度MD(F)期望值为E[MDt+1(F)]，即

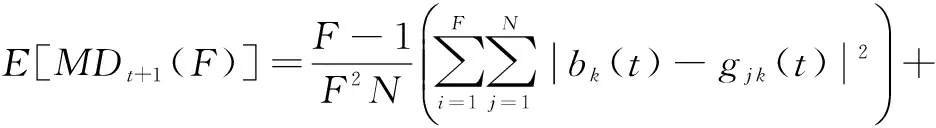
(13)

式中：MDt(g(t))表示g(t)离散度。

证明根据式(12)有

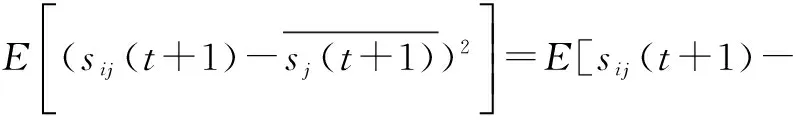
(14)

又因

(15)

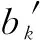
(16)

联立式(12)以及式(14)～式(16)，有

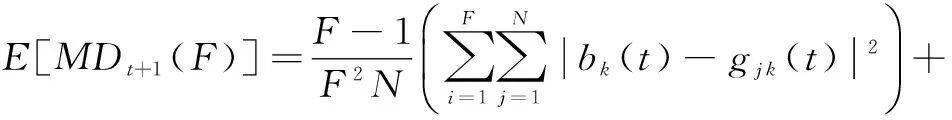
(17)

证毕。

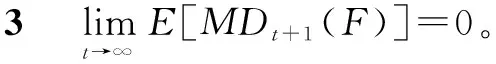
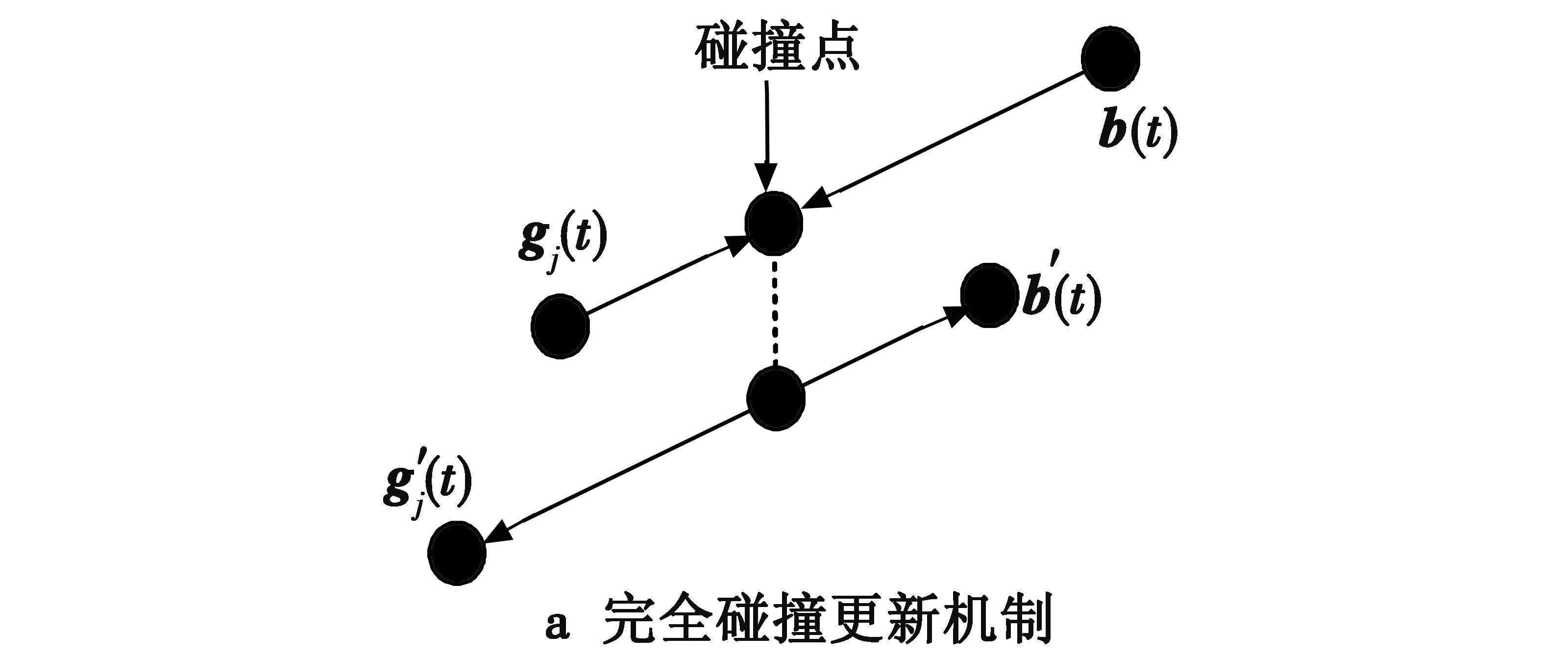
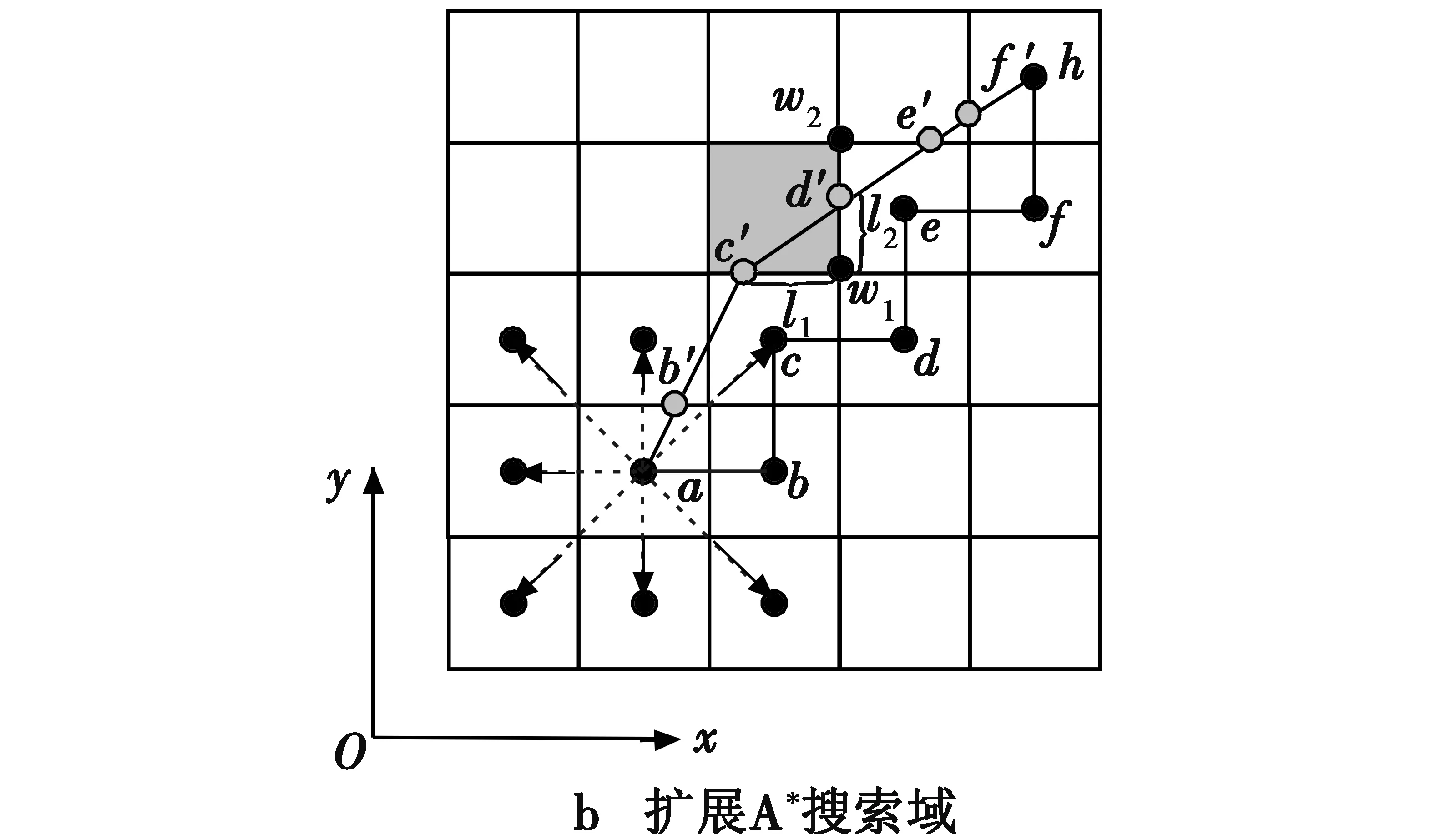
图2 “完全弹性碰撞”与A*搜索域扩展示意图Fig.2 Perfect elastic collision and A* search domain extension

2.2.2 自适应跳跃机制

t时刻，选取种群适应度最优的前F1个进行跳跃更新，更新公式为

(18)

F1=⎣F1,min+α(F1,max-F1,min)」e(ln 2t/Tmax-1)

(19)

式中：δ为(0,1)随机数；ζ为跳跃指数；Sj,min，Sj,max和F1,min，F1,max分别为对应变量最小值和最大值。个体采用式(18)更新后得到新的个体Snew，若适应度优于原个体则取代原个体，否则保持不变。

从式(18)和式(19)可以看出，F1和个体更新概率p随着迭代次数增加，参数取值不断自适应调整，从而有效提高了较优个体扰动跳跃概率，为算法寻找到全局最优解提供了可能。

2.3 多策略SSO优化航迹规划模型实现

采用极坐标对空间进行处理，不仅可以满足最小航程约束条件，而且只需要得到系列θi就可以得到航迹节点信息，进而实现航迹规划。

定义4对于蜘蛛个体，定义其编码方式为Si=(θ1,θ2,…,θM)。

定义5对于蜘蛛个体，定义其目标函数为航迹综合代价模型，即

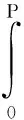
(20)

(21)

式中：ΔΨi为航迹节点偏航角；Ψmax为最大偏航角。

基于MSSSO的静态航迹规划实现流程见图3。

图3 静态航迹规划实现流程Fig.3 Realization process of static route planning

3 突发威胁动态航迹规划实现

在执行设定任务飞行时，无人机往往会受到突发威胁，这就要求其能够自主完成突发威胁航迹重规划，因此对重规划实时性要求较高。本文采用A*算法[13]执行突发威胁航迹重规划过程，以生成新的局部航迹。

3.1 改进A*算法

A*算法隶属启发式搜索算法范畴[14]，其通过代价函数f(n)对搜索区域内节点进行评估，从而筛选出最佳路径节点列表，进而实现路径规划。代价函数f(n)算式为

f(n)=h(n)+g(n)

(22)

式中：n为搜索区域可扩展节点；h(n)为起始节点到n的实际代价；g(n)为n到目标点的估计代价。由于基本A*算法设定扩展搜索区域为网格中心，因此规划出的路径不是最短路径，而且弯折较多，这无形中增大了无人机飞行难度(如图2b所示的a→b→…→h路径)，因此引入最小“弯折”估计代价函数并拓展A*算法搜索邻域个数，从而得到更加平滑的局部航迹。

3.1.1 最小“弯折”估计代价

无人机局部航迹规划在尽量要求航程最短的同时希望弯折程度最小，为此引入弯折程度代价，改进后的h(n)算式为

(23)

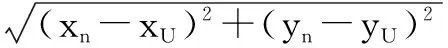
3.1.2 搜索邻域节点扩展

将网格边线进行H等分，因此得到H+1个节点，规定每条网格边线上的H+1个节点为搜索可扩展节点。为了进一步降低f(n)计算量，提高算法运算速度，不需要全部计算出所有线段点上的代价函数值，而是利用网格中心点和边线交点的代价值进行估算，以图2b中的c′点为例，d′为其可扩展点，c′与d′距离最近边线交接点w1的距离分别为l1和l2(设网格边线长度为1)，当c′向d′扩展时，代价函数f(d′)为

(24)

式中,g(c′,d′)为c′，d′所在网格中心的估计代价。

3.2 改进A*算法突发威胁动态航迹规划实现

采用改进的A*算法对突发威胁航迹进行重规划，分别设置OPEN和CLOSED存储已生成且没有考察的节点和已经访问过的节点。图4给出了基于改进A*算法突发威胁动态航迹规划实现流程图。

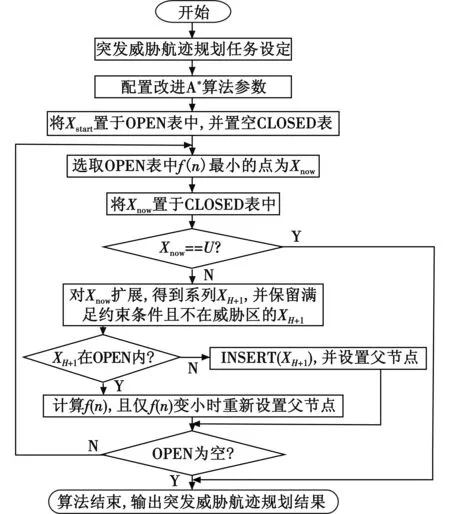
图4 突发威胁动态航迹规划实现流程Fig.4 Realization process of sudden threat dynamic route planning

4 实验仿真

4.1 静态航迹规划实例仿真

为验证分析MSSSO静态航迹规划算法性能，采用Matlab仿真平台对实例进行仿真实验：在70 km×70 km二维空间内，无人机从(15 km,23 km)处起飞执行对(47 km,53 km)处敌方指挥中心打击任务。MSSSO相关参数设置如下：ωO=0.15,ωH=0.05,ωr=0.30,ωm=0.30,ωg=0.10,ωa=0.05,ωe=0.05,n=10,F=200,F1,min=10,F1,max=30,ρ=2 km，无人机飞行性能参数参考文献[7]，雷达、高炮、导弹、大气威胁参数设置参考文献[10]，地形威胁采用不规则图形进行表示。为进一步分析MSSSO性能，分别采用基本SSO算法、粒子群优化算法(PSO)和MSSSO进行对比实验，每种算法独立运行50次，对比分析最终航迹结果(利用K平滑算法对3种算法航迹进行处理)。表1给出了3种算法相关指标对比结果，图5给出了3种算法航迹规划以及收敛曲线对比结果。

从图5可以看出，MSSSO和PSO都能给出合理无人机静态航迹规划结果，但是SSO规划的航迹穿越了地形威胁，会对无人机带来较大威胁。从3种算法性能指标和收敛曲线对比结果可以看出，无论是总航程、航迹代价还是算法运算时间，MSSSO都要优于其他两种算法，这是因为MSSSO引入完全弹性碰撞机制，个体直接向种群最优解和自身历史最优解学习，提高了进化速率，而且在算法运算后期，自适应跳跃机制改善了算法全局深度寻优能力，提高了算法收敛精度。

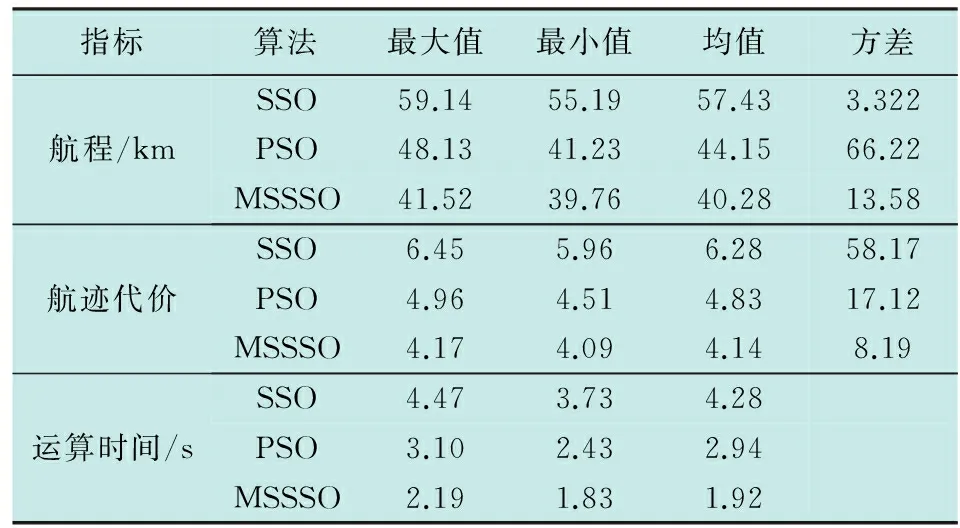
表1 SSO,MSSSO和PSO性能对比

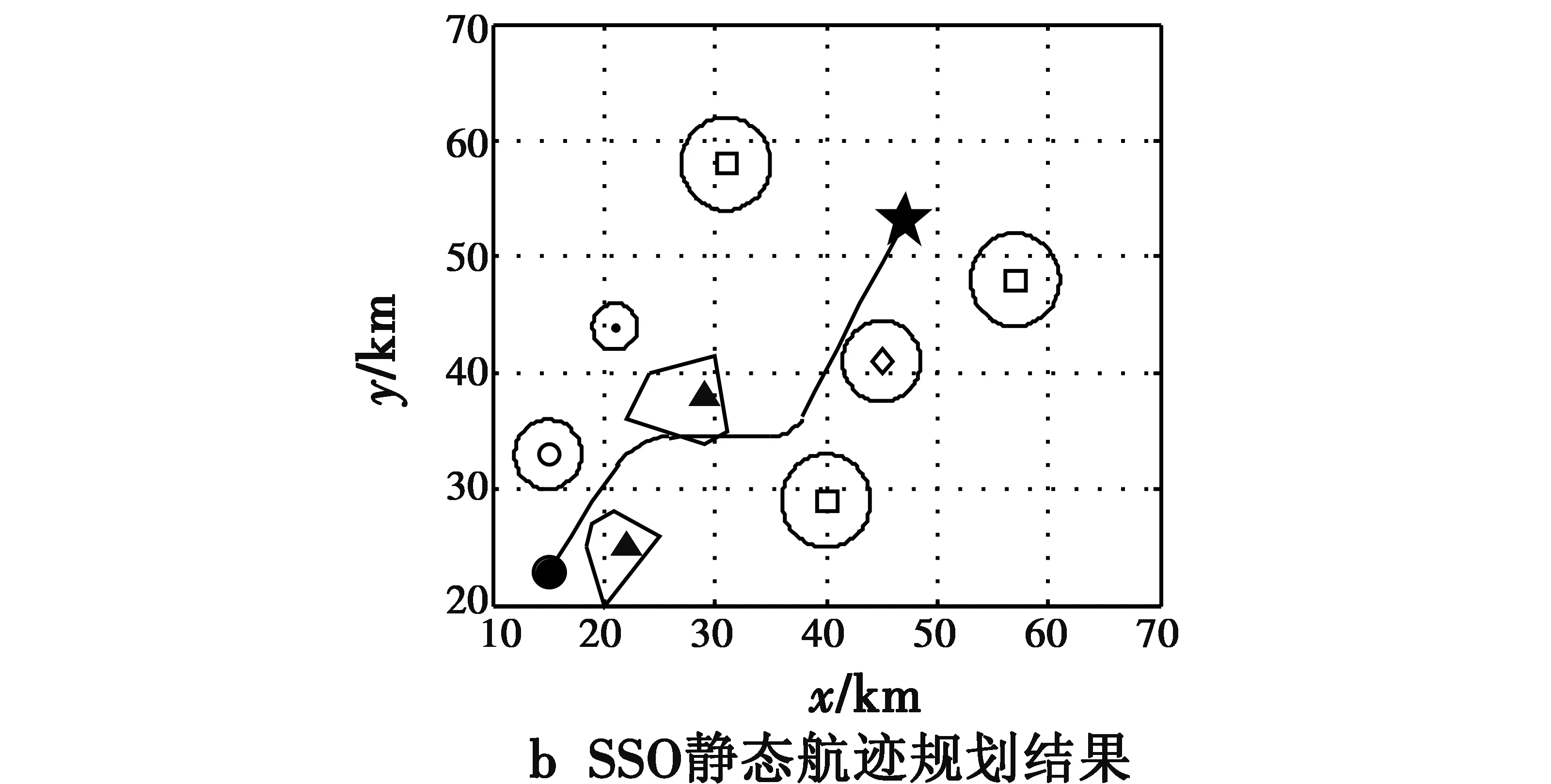
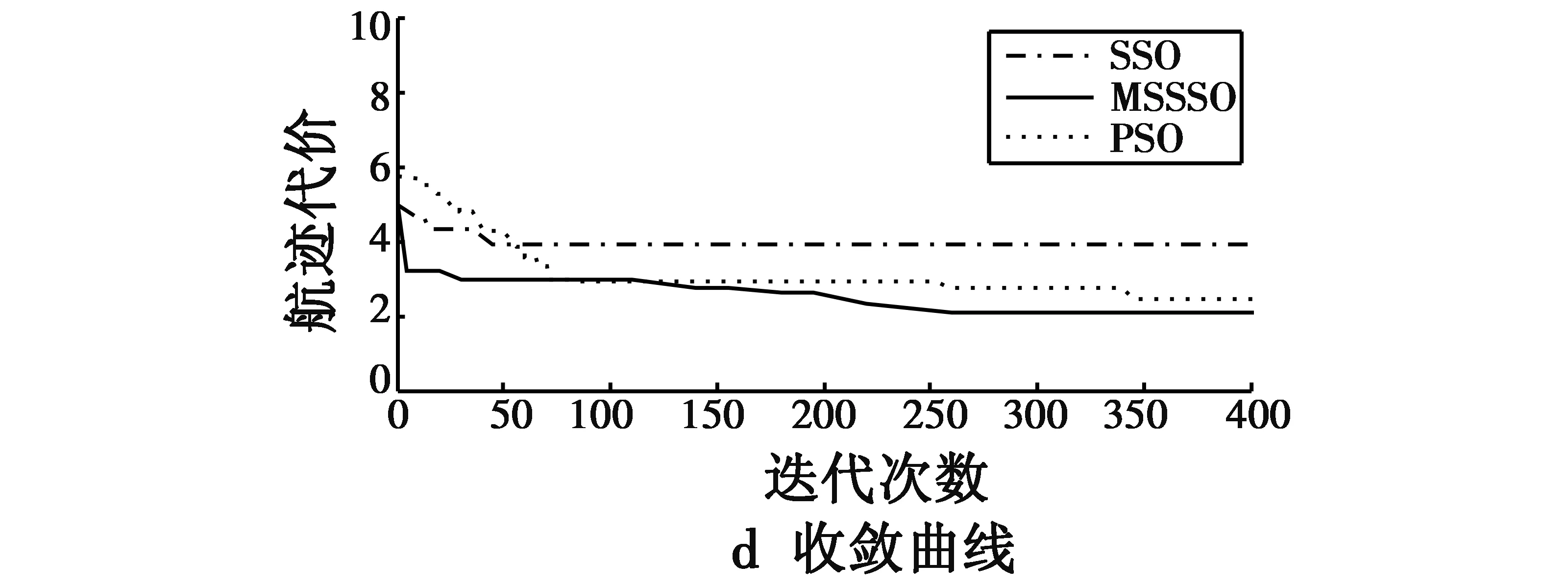
图5 3种算法航迹规划以及收敛曲线对比结果Fig.5 Path planning and convergence curves of 3 algorithms

4.2 突发威胁动态航迹规划实例仿真

无人机按照4.1节规划航迹进行飞行，当飞行到(19 km,27 km)时探测到(25 km,31 km)处出现新的大气威胁，如果无人机仍按照设定航迹继续飞行，将会进入大气威胁范围内，导致损毁概率极大，因此无人机需要进行突发威胁航迹重规划，此时设定重规划起始点为(19 km,27 km)，终止点为原来航迹中的(29 km,33 km)，采用改进A*算法进行求解，图6给出了重规划后的无人机航迹以及与A*算法局部航迹动态规划对比结果。

图6 突发威胁1动态航迹规划实例仿真Fig.6 Dynamic path planning for sudden threat 1

从图6可以看出，无人机能够避开大气威胁，继续向前飞行，而且再规划航迹相对平滑，而采用A*算法规划后的航迹弯折较多，不利于无人机机动飞行。当无人机飞行到(36 km,41 km)位置时，发现(43 km,43 km)处出现了新的导弹威胁，而且无人机刚好经过其有效射程，因此需要再次重规划，规划起始位置设定为(36 km,41 km)，终止点设定为目标点。图7给出了再次重规划后的无人机航迹以及与A*算法局部航迹动态规划对比结果。从图7可以看出，与突发威胁1航迹重归化结果一样，改进A*算法得到的动态规划结果能够避开威胁，而且航迹更利于无人机在相对较短范围内机动。

为了进一步分析改进A*算法性能，分别对突发威胁1和突发威胁2独立运行50次，表2给出了改进A*与A*算法性能指标对比结果。从表2可以看出，对于局部规划航程，改进A*算法要明显好于A*算法；对于算法运算时间，A*算法要快于改进A*算法，这是因为改进A*算法扩展了领域搜索范围，增加了算法运算量，但是以无人机最大150 km/h速度为例，在改进A*算法运算时间内，无人机最多移动了9.58 m(150×1000×0.23/3600)，约占局部规划网格长度1 km的1%，因此符合实际飞行环境。

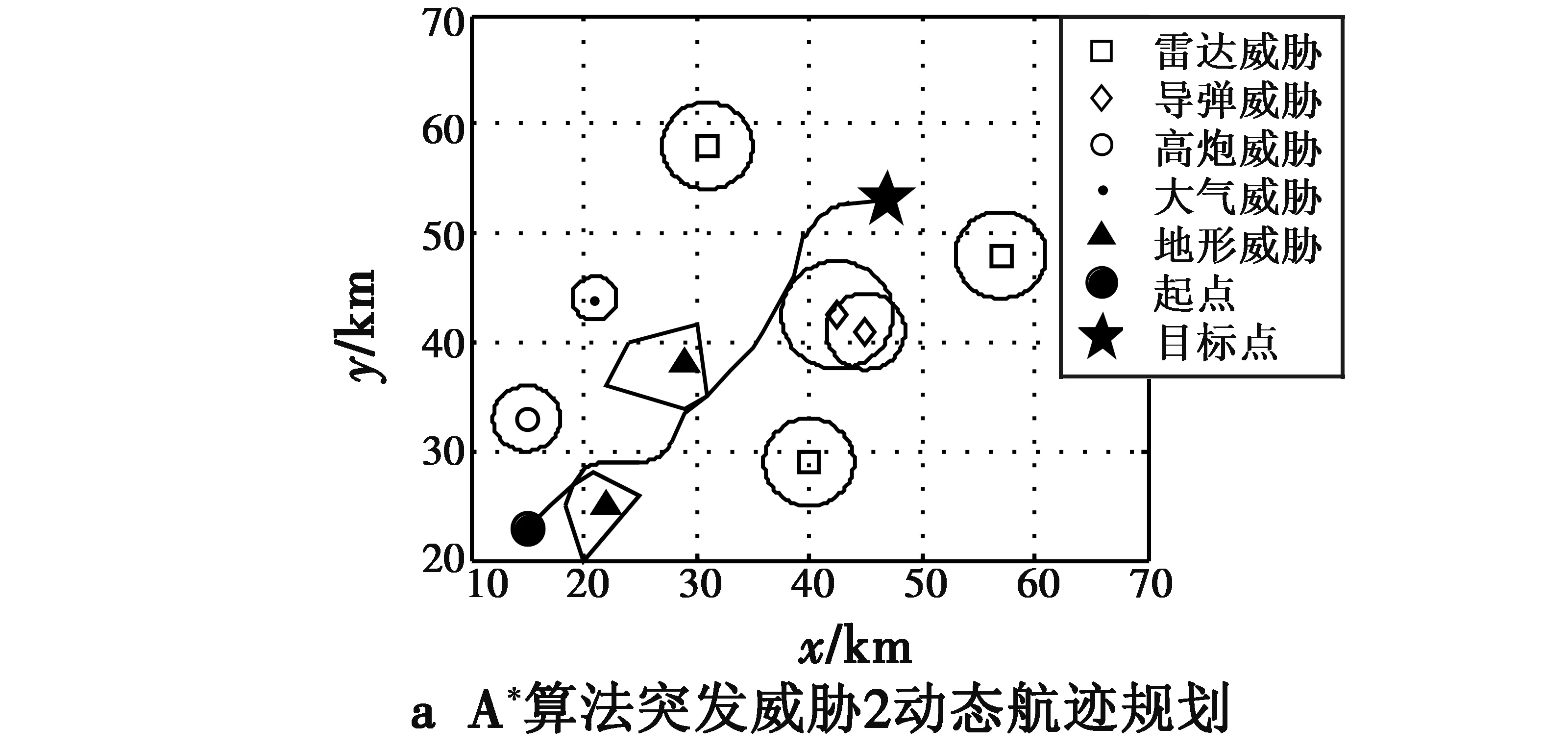
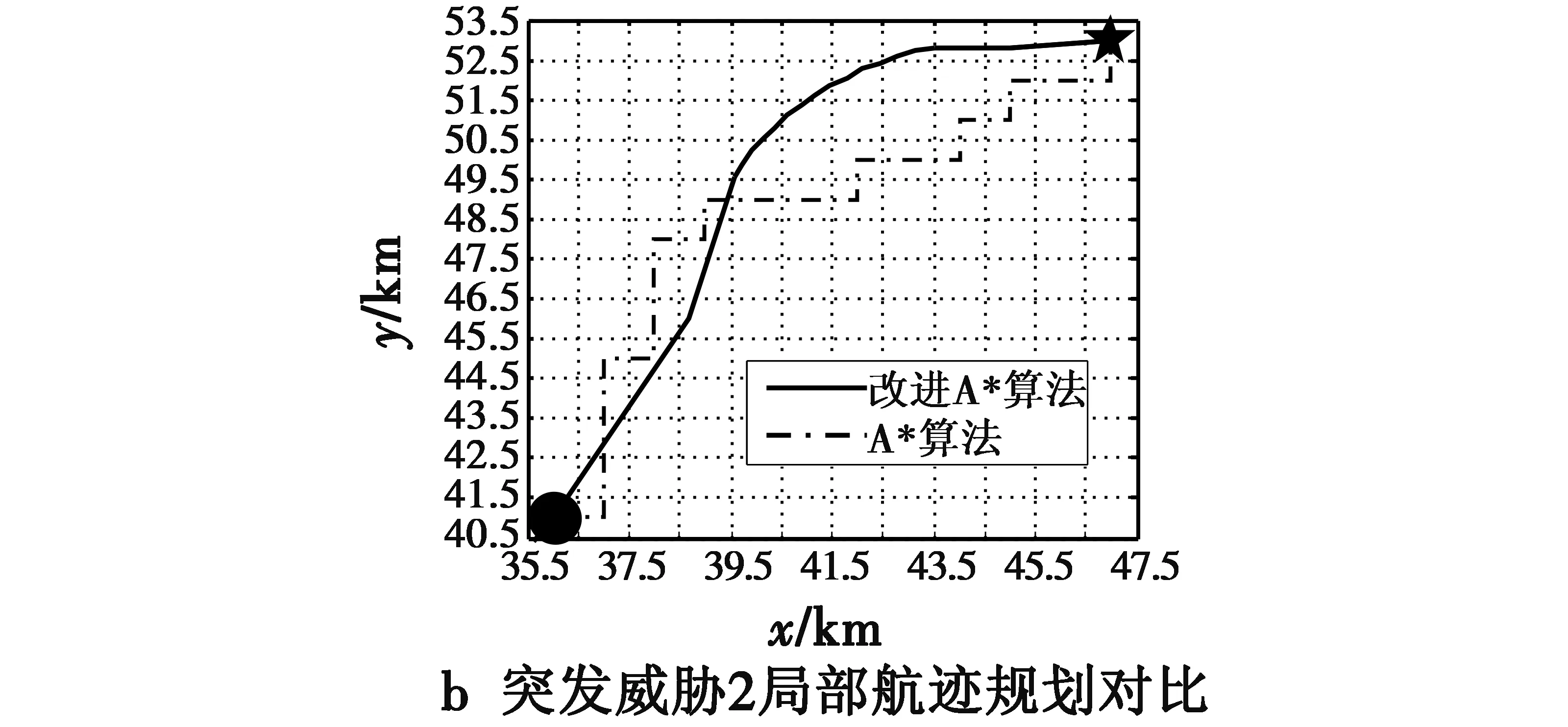
图7 突发威胁2动态航迹规划实例仿真Fig.7 Dynamic path planning for sudden threat 2

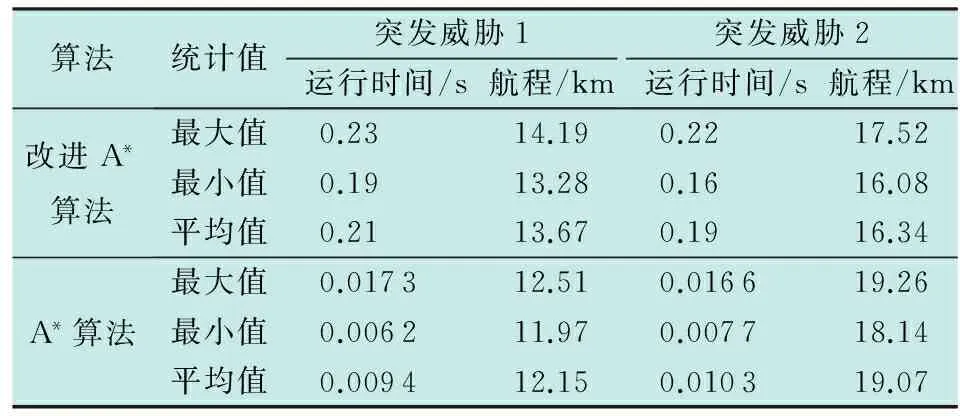
算法统计值突发威胁1运行时间/s航程/km突发威胁2运行时间/s航程/km改进A*算法最大值0.2314.190.2217.52最小值0.1913.280.1616.08平均值0.2113.670.1916.34A*算法最大值0.017312.510.016619.26最小值0.006211.970.007718.14平均值0.009412.150.010319.07

5 结束语

提出了一种基于多策略SSO和改进A*算法的无人机动态航迹规划方法，该方法通过引入完全弹性碰撞、自适应跳跃机制、最小“弯折”估计代价函数以及拓展A*算法搜索邻域个数等策略，实现了对无人机动态航迹规划，仿真实例实验结果也表明了该方法的有效性，下一步工作重点将围绕多机协同航迹规划问题展开。

[1] KALYANAM K,CHANDLER P,PACHTER M,et al.Opti-mization of perimeter patrol operations using unmanned aerial vehicles[J].Journal of Guidance,Control,and Dynamics,2012,35(2):434-441.

[2] 方群，徐青.基于改进粒子群算法的无人机三维航迹规划[J].西北工业大学学报，2017，35(1)：66-73.

[3] 齐乃明，孙小雷，董程，等.航迹预测的多无人机任务规划方法[J].哈尔滨工业大学学报，2016，48(4)：32-36.

[4] LI Q R,WEI C,WU J,et al.Improved PRM method of low altitude penetration trajectory planning for UAVs[C]//Proceeding of the IEEE Chinese Guidance,Navigation and Control Conference,2014:2651-2654.

[5] 曾国奇,赵民强,刘方圆,等.基于网格PRM的无人机多约束航路规划[J].系统工程与电子技术,2016,38(10):2310-2316.

[6] 尹高扬，周绍磊，吴青坡.无人机快速三维航迹规划算法[J].西北工业大学学报，2016,34(4)：564-570.

[7] 孙小雷，齐乃明，董程，等.无人机任务分配与航迹规划协同控制方法[J].系统工程与电子技术，2015，37(12)：2772-2776.

[8] OZALP N,SAHINGOZ O K.Optimal UAV path planning in a 3D threat environment by using parallel evolutionary algorithms[C]//Proceeding of the IEEE International Conference on Unmanned Aircraft Systems,2013:308-317.

[9] 韩攀，陈谋，陈哨东，等．基于改进蚁群算法的无人机航迹规划[J].吉林大学学报:信息科学版，2013,31(1)：66-72.

[10] 张帅，李学仁，张建业,等.基于动态步长的无人机三维实时航迹规划[J].北京航空航天大学学报,2016,42(12):2745-2754.

[11] CUEVAS E,CIENFUEGOS M,ZALDIVA D R,et al.A swarm optimization algorithm inspired in the behavior of the social spider [J].Expert System with Applications, 2013,40(16):6374-6384.

[12] 王艳娇，李晓杰，肖婧.基于动态学习策略的群集蜘蛛优化算法[J].控制与决策，2015，30(9)：1575-1582.

[13] HART P E,NILSSON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107.

[14] 占伟伟，王伟，陈能成，等.一种利用改进A*算法的无人机航迹规划[J].武汉大学学报:信息科学版，2015，40(3)：315-320.

DynamicPathPlanningforUAVsBasedonMulti-strategySSOandImprovedA*Algorithm

TIAN Kuo, LIU Xu

(Chinese Flight Test Establishment,Xi’an 710089,China)

In order to solve the problems of dynamic path planning for Unmanned Aerial Vehicles (UAVs) confronted with sudden threats,a dynamic UAV path-planning method is proposed based on multi-strategy SSO (Social Spider Optimization) and the improved A*algorithm.The UAV path planning is divided into two stages: static path planning and real-time evasion under sudden threat.At the stage of static path planning,multi-strategy SSO optimization algorithm is used to solve the polar-coordinate path-planning model,and the mechanisms of perfect elastic collision and adaptive skipping are introduced,which can improve the feasibility of the path-planning results while satisfying the restraints of flight performance.At the stage of real-time evasion under unexpected threat,the improved A*algorithm is used for path planning in local regions for a second time.Through expanding the number of neighborhood for A*algorithm and introducing the minimum “bent” estimation cost function,a smoother optimal path can be obtained while satisfying the real-time requirements.The simulation results show that the proposed method can provide more satisfactory dynamic path-planning for UAVs.

path planning; Unmanned Aerial Vehicle (UAV); social spider optimization; improved A*algorithm

田阔，刘旭.基于多策略SSO 和改进A*算法的无人机动态航迹规划[J].电光与控制，2017，24( 11) : 31-37.TIAN K，LIU X.Dynamic path planning for UAVs based on multi-strategy SSO and improved A*algorithm[J].Electronics Optics & Control，2017，24( 11) : 31-37．

2017-04-22

2017-05-26

田 阔(1984 —),男，河南郑州人,硕士，工程师，研究方向为探测与制导。

V19

A

10.3969/j.issn.1671-637X.2017.11.007