均方根容积代价参考粒子滤波算法

武青海 ，曲朝阳

(1.吉林农业科技学院电气与信息工程学院，吉林 吉林 132101； 2.东北电力大学信息工程学院，吉林 吉林 132012)

均方根容积代价参考粒子滤波算法

武青海1，曲朝阳2

(1.吉林农业科技学院电气与信息工程学院，吉林 吉林 132101； 2.东北电力大学信息工程学院，吉林 吉林 132012)

为提高复杂噪声的滤波精度，基于均方根容积卡尔曼滤波(SCKF)和代价参考粒子滤波(CRPF)，提出一种新的均方根容积代价参考粒子滤波算法(SCCRPF)。算法采用SCKF和最新量测信息更新先验分布函数，生成CRPF的重要密度函数，保留了SCKF对非线性系统的滤波精度，同时获取了CRPF对噪声假设未知系统的滤波精度。仿真结果表明，对于噪声假设未知系统，SCCRPF的滤波精度高于均方根容积粒子滤波(SCPF)；对于噪声假设已知系统，SCCRPF的滤波精度高于CRPF。

状态估计； 非线性系统； 非高斯系统； 代价参考粒子滤波

0 引言

状态估计问题在视景跟踪、机器人定位、航海以及其他领域得到广泛研究。对于非线性系统，常用的估计方法是扩展卡尔曼滤波(EKF)[1-2]、不敏卡尔曼滤波(UKF)[3-4]、均方根容积卡尔曼滤波(Square-root Cubature Kalman Filter,SCKF)[5-6]。但以上都是假设过程噪声和量测噪声为高斯白噪声，在非高斯噪声条件下的滤波效果就会很差。对于非线性非高斯系统，基于贝叶斯理论和蒙特卡罗方法的粒子滤波(Particle Filter,PF)[7-8]能够获取好的滤波效果。

为提高复杂噪声系统的滤波精度，学者们提出了不依赖任何分布函数先验知识的代价参考粒子滤波(Cost-Reference Particle Filter,CRPF)[9-10]。但在量测信息较为精确的条件下，CRPF的滤波精度可以通过融合最新量测信息进行改进。

通过将SCKF引入CRPF框架下提出了SCCRPF，利用最新量测信息，通过SCKF来产生重要性密度函数(Importance Density Function,IDF)，在量测信息相对准确条件下，IDF更加接近真实的后验概率分布。SCCRPF不仅能够处理噪声假设未知的系统，同时获取了SCKF对非线性系统的滤波精度。仿真结果表明，对噪声条件复杂的系统，SCCRPF具有更高的滤波精度。

1 SCCRPF

CRPF的粒子从IDF里采样，IDF的确定对CRPF十分重要，目前较为流行的方法是采用状态转移先验分布，因为其计算较为简单，但这种方法未能包含最新的量测信息。在量测信息相对准确条件下，采用SCKF等方法对粒子进行传递，可进一步提升CRPF的滤波精度，如扩展粒子滤波(EPF)[11]和不敏粒子滤波(UPF)[12]的精度要比传统PF高。

以SCKF作为子滤波器，完成CRPF中粒子传递过程，提出新的SCCRPF，其过程如下。

1.1 初始化

在k=0时刻，从初始分布中均匀抽取N个粒子，即

xj0～u(I0)j=1,2,…,N。

(1)

为保证粒子多样性，I0的选取应足够大。计算各个粒子初始协方差的开方Sj0，即

(2)

(3)

Pj0=Sj0(Sj0)T。

(4)

对各粒子初始代价赋值

cj0=0 。

(5)

得到初始样本集合

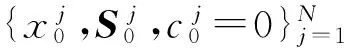
(6)

1.2 重采样

已知k时刻的粒子集合为

(7)

结合k+1时刻的量测zk+1，计算各个粒子的风险，即

δjk+1=λcjk+Δc(xjk|zk+1)

(8)

式中：λ为遗忘因子，主要作用平衡历史信息和当前信息的权重，其值越大历史信息占比重越大，反之历史信息比重越小;增量部分的计算形式为

Δc(xjk|zk+1)=‖zk+1-h(f(xjk))‖p

(9)

式中,p可取1或2。当得到各个粒子的风险后，计算粒子的概率混合密度函数(Probability Mass Function,PMF),即

(10)

式中,u(δjk+1)的计算式为

u(δjk+1)=1/(δjk+1-minj{δjk+1}+α)β

(11)

式中，β=2，且有

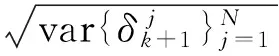
(12)

(13)

1.3 利用SCKF完成粒子传递

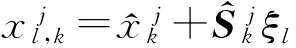
(14)

传递各粒子的容积点

xj+l,k=f(xjl,k) 。

(15)

估计各粒子的预测状态

(16)

估计各粒子

(17)

式中:Tria()为求预测协方差的开方的操作，具体操作见文献[5-6];SjQ为第j个粒子的状态协方差的开方，且有

(18)

量测更新：由于Sjk+1|k已知，直接计算各粒子的容积点(l=1,2,…,2n),即

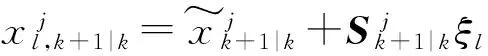
(19)

传递各粒子的容积点

zj+l,k+1|k=h(xjl,k+1|k) 。

(20)

估计各粒子的预测量测

(21)

估计各粒子新息协方差的开方

(22)

式中,SjR为第j个粒子量测协方差的开方，且有

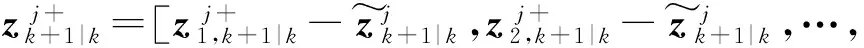
(23)

估计各粒子的交叉协方差为

Pjxz,k+1|k=xj++k+1|k(zj+k+1|k)T。

(24)

且有

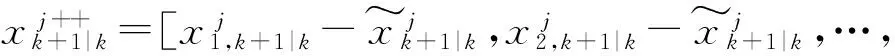
(25)

计算各粒子的增益为

Φjk+1=Pjxz,k+1|k(Sjzz,k+1|k(Sjzz,k+1|k)T)-1。

(26)

估计各粒子的状态为

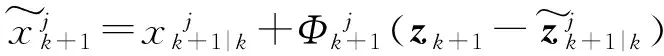
(27)

估计各粒子协方差的开方为

(28)

经过SCKF传递后，新的粒子包含了最新的量测信息，基于传递后的状态和协方差开方，产生粒子

(29)

对各粒子的代价进行更新，有

(30)

式中,

Δc(xjk+1|zk+1)=‖zk+1-h(xjk+1)‖p。

(31)

经过粒子传递过程，得到更新后的粒子及其代价集合

(32)

1.4 状态估计

对每个粒子分配PMF

为使A相剩磁稳定，需使合闸时刻外加电源A相虚拟磁链正好处在对应方向的峰值，若剩磁为负，则为负峰值，反之亦然。假设剩磁为某一值X，则要求剩磁满足：

(33)

式中,

u(cjk+1)=1/(cjk+1-minj{cjk+1}+α)β。

(34)

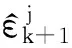
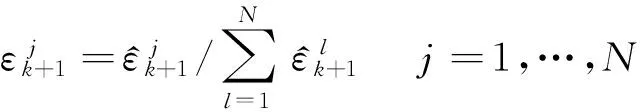
(35)

状态估计为

(36)

2 仿真结果与分析

为了验证所提SCCRPF的有效性，进行仿真并与CRPF,SCPF比较。所采用的系统的状态方程为

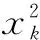
(37)

量测方程为

(38)

初始状态为x0～N(10,0.8),所有的粒子数目为500,采用的重采样方法为残差重采样，蒙特卡罗仿真次数为50次,遗忘因子λ=0.85，且p=2。

首先，在噪声假设已知条件下，将CRPF与SCCRPF进行比较，以说明利用SCKF进行CRPF粒子传递的效果；其次，在噪声假设未知条件下，将SCPF与SCCRPF进行比较，说明后二者兼顾着CRPF对噪声未知条件的处理能力。

2.1 噪声假设已知

噪声假设为

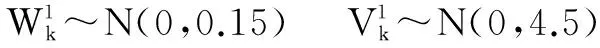
(39)

分别采用CRPF和SCCRPF对系统进行跟踪，其中，CRPF与SCCRPF的跟踪结果对比如图1所示。

图1 CRPF与SCCRPF的比较Fig.1 Comparison of CRPF with SCCRPF

从图1可以看出，CRPF和SCCRPF均可有效跟踪目标，在噪声假设已知条件下，SCCRPF的精度同样优于CRPF，对其跟踪误差的RMSE数据进行统计分别为1.852和1.653。

2.2 噪声假设未知

状态噪声假设与噪声假设已知情况相同，量测噪声由已知部分和未知部分组成，即

V2k=V2k,known+V2k,unknown

(40)

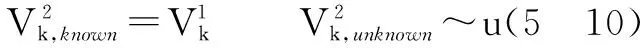
(41)

同理，将SCCRPF与采用SCKF完成粒子传递的SCPF进行比较，结果如图2所示。从图2可以看出，SCCRPF的滤波精度高于SCPF。对其跟踪误差RMSE数据进行统计分别为8.687和6.228。

图2 SCPF与SCCRPF的比较Fig.2 Comparison of SCPF with SCCRPF

从仿真实验可以看出，利用SCKF传递CRPF的粒子，提升了对已知噪声滤波精度，同时，SCCRPF获得了CRPF对未知噪声的处理能力，新的非线性非高斯滤波在处理复杂噪声方面具有更好的整体性能。

3 结论

通过对SCKF和CRPF的融合，提出了一种SCCRPF，新算法采用了最新量测信息完成CRPF粒子的传递，提升了IDF对真实后验概率分布的逼真度，提高了滤波精度。仿真结果亦验证了SCCRPF的有效性。

[1] ZHANG K W,CHEN J C,CHANG Y F,et al.EKF-based LQR tracking control of a quadrotor helicopter subject to uncertainties[C]//IECON 42nd Annual Conference of IEEE Industrial Electronics Society,2016:5426-5431.

[2] YANG S K,LI H X.Application of EKF and UKF in target tracking problem[C]//The 8th International Conference on Intelligent Human-Machine Systems and Cybernetics,2016:116-120.

[3] CHEN J,SONG J,LI L,et al.UKF-based adaptive variable structure observer for vehicle sideslip with dynamic correction[J].IET Control Theory and Applications, 2016,10(14):1641-1652.

[4] DIAZ A O C,SANTOS A I G.State estimation of the switched reluctance motor MFR 132.5 with MHE and UKF estimators[J].IEEE Latin America Transactions, 2016,14(1):147-152.

[5] LI C,GE Q B.SCKF for MAV attitude estimation[C]//International Conference on Machine Learning and Cybernetics,2011:1313-1318.

[6] 林浩申，黄璜，刘刚，等.基于SCKF算法的空间机动目标跟踪研究[J].电光与控制,2015,22(3):64-68.

[7] SONG Z Q,FU P,LI J C,et al.Prototype design and test of ITER PF converter unit[J].IEEE Transactions on Plasma Science,2016,44(9):1677-1683.

[8] YOUN H S,LEE J B,BAEK J,et al.A digital phase leading filter current compensation (PLFCC) technique for CCM boost PFC converter to improved PF in high line voltage and light load conditions[J].IEEE Transactions on Power Electronics,2016,31(9):6596-6606.

[9] LIM J,HONG D.Cost reference particle filtering approach to high-bandwidth tilt estimation[J].IEEE Transaction on Industrial Electronics,2010,57(11):3830-3839.

[10] 董唯光,李言俊,张科.改进的CRPF在自主天文导航中的应用[J].计算机测量与控制,2008,16(11):1682-1684,1688.

[11] 王秋平,周原,康顺,等.改进权值计算的EPF算法及在目标跟踪中的应用[J].电光与控制,2011,18(4):10-12,25.

[12] 申正义,王晴晴,许诚,等.UPF改进算法在单站无源定位中的应用[J].雷达科学与技术,2014,12(6):592-596,603.

Square-RootCubatureCost-ReferenceParticleFilterAlgorithm

WU Qing-hai1, QU Zhao-yang2

(1.School of Electrical and Information Engineering,Jilin Agricultural Science and Technology University,Jilin 132101,China;2.School of Information Engineering,Northeast Dianli University,Jilin 132012,China)

To improve the filtering precision under complex noise condition,a new Square-root Cubature Cost-Reference Particle Filter (SCCRPF) is proposed based on the Square-root Cubature Kalman Filter (SCKF) and the Cost-Reference Particle Filter (CRPF).The proposed filter updates the prior distribution function with the latest measured information and SCKF,and thereby generates the importance density function for CRPF.The new filter not only reserves the precision advantage of SCKF in filtering nonlinear systems,but also possesses the filtering precision of CRPF for dealing with systems with an unknown noise assumption.Simulation results show that:the filtering precision of SCCRPF is higher than that of Square-root Cubature Particle Filter (SCPF) for a system with unknown noise assumption,and is higher than that of CRPF for a system with known noise assumption.

state estimation; nonlinear system; non-Gaussian system; cost-reference particle filter

武青海，曲朝阳.均方根容积代价参考粒子滤波算法[J].电光与控制，2017，24( 11) : 28-30，42.WU Q H，QU Z Y.Square-root cubature cost-reference particle filter algorithm[J].Electronics Optics & Control，2017，24( 11) : 28-30，42．

2017-01-03

2017-01-16

吉林省教育科学重点项目(ZD115088)

武青海(1978—),男，黑龙江双城人，硕士，讲师，研究方向为算法分析与设计、软件工程。

TP391.41

A

10.3969/j.issn.1671-637X.2017.11.006