多项式模糊系统混合H2/H∞控制

马清亮， 杨海燕， 吴旭光

(1.火箭军工程大学控制工程系，西安 710025； 2.西北工业大学航海学院，西安 710072)

多项式模糊系统混合H2/H∞控制

马清亮1， 杨海燕2， 吴旭光2

(1.火箭军工程大学控制工程系，西安 710025； 2.西北工业大学航海学院，西安 710072)

对于多项式模糊系统，提出一种具有公共Lyapunov矩阵的混合H2/H∞性能准则。基于多项式Lyapunov函数与平方和分解技术，推导出多项式模糊系统混合H2/H∞状态反馈控制器的存在条件。通过求解一个具有多项式平方和约束的参数极小化问题，给出了混合H2/H∞模糊控制器优化设计方法。

多项式模糊系统； 混合H2/H∞控制； 多项式Lyapunov函数； 平方和优化

0 引言

多项式模糊模型是在T-S模糊模型基础上提出的一种用于描述非线性系统的新型模糊模型[1]。传统T-S模糊模型的后件采用线性方程描述，采用T-S模糊模型，能够逼近任意光滑的非线性系统。作为T-S模糊模型的推广，多项式模糊模型在整体结构上与T-S模糊模型类似。由于采用了多项式非线性方程作为模糊模型的后件，因此，运用多项式模糊模型能够更有效地描述复杂非线性系统。对于T-S模糊系统，通常采用二次Lyapunov函数和线性矩阵不等式(LMI)技术设计模糊控制器；而对于多项式模糊系统，则采用多项式Lyapunov函数与多项式平方和(SOS)优化技术设计模糊控制器，因而能够降低模糊控制器设计的保守性[2]。目前，已有学者针对多项式模糊系统的镇定控制、鲁棒

混合H2/H∞控制是具有H∞性能约束的H2优化控制问题。在控制器设计过程中，混合H2/H∞控制同时考虑系统的H2性能和H∞性能，因而能够使闭环系统一方面具有较强的鲁棒性，另一方面又获得优良的调节性能。对于多项式模糊系统的混合H2/H∞控制问题，目前相关研究成果尚不多见。

本文在文献[7]的基础上，进一步研究多项式模糊系统的混合H2/H∞状态反馈控制器设计问题。首先提出一种具有公共Lyapunov矩阵的多项式模糊系统混合H2/H∞性能准则；进而，基于多项式Lyapunov函数与平方和优化技术，给出了混合H2/H∞状态反馈模糊控制器的存在条件和优化设计方法。

1 问题描述

考虑如下非线性系统

(1)

式中：x(t)∈Rn为状态向量；f和g是光滑非线性函数；u(t)∈Rm是控制输入；w(t)∈Rp是能量有界的外部干扰；z∞(t)∈Rq是控制输出。

构建描述式(1)非线性系统的多项式模糊模型，第i条模糊规则如下[1]所述。

Ifz1(t) isMi1and … andzp(t) isMip,then

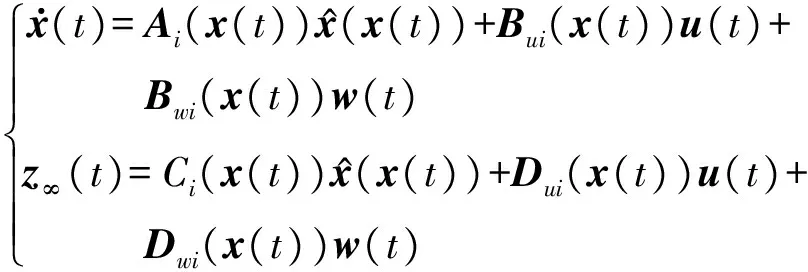
(2)

对式(2)的多项式模糊模型进行反模糊化处理，可得到全局多项式模糊系统

(3)

根据平行分布补偿原理，对于式(3)的多项式模糊系统，可设计如下形式的状态反馈模糊控制器，即

。

(4)

结合式(3)和式(4)，可得相应的闭环多项式模糊系统为

(5)

。

(6)

对于式(3)的多项式模糊系统，本文研究目标是确定模糊控制器式(4)中增益矩阵Ki(x)(i=1,…,r)，使得式(5)的闭环模糊系统是稳定的，同时满足如下性能指标。

2)H2性能：由式(6)定义的系统H2性能指标达到最小。

2 多项式模糊系统混合H2/H∞性能分析

本章在分析多项式模糊系统H2性能和H∞性能的基础上，提出一种基于公共Lyapunov矩阵的多项式模糊系统混合H2/H∞性能准则。

2.1 多项式平方和分解

定义1对于多元多项式f(x)，其中x∈Rn，若存在一组多项式g1(x),g2(x),…,gm(x)，使得

(7)

则称f(x)为平方和(SOS)多项式[7]。

记ΣSOS表示所有平方和多项式的集合。若f(x)∈ΣSOS，则有f(x)≥0成立。

引理1[8]设f(x)是一个阶次为2d的多元多项式，其中,x∈Rn；Z(x)是一个由x的单项式(阶次不高于d)构成的列向量，则f(x)是SOS多项式的充要条件是存在一个半正定矩阵Q，满足

f(x)=ZT(x)QZ(x)

。

(8)

引理2设F(x)是一个次数为2d的N×N维对称多项式矩阵，其中：x∈Rn，Z(x)是一个由x的单项式(次数不高于d)构成的列向量，考虑如下3个条件[7,9]：1)F(x)≥0对于∀x∈Rn均成立；2)vTF(x)v是SOS多项式，其中，实向量v∈RN与x不相关；3) 存在一个半正定矩阵Q，满足vTF(x)v=(v⊗Z(x))T·Q(v⊗Z(x))，其中，“v⊗Z(x)”表示向量v与Z(x)的Kronecker积。则有：1)⟸2)；2)⟺3)。

2.2 多项式模糊系统的H2性能准则

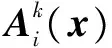
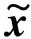
(9)

(10)

(11)

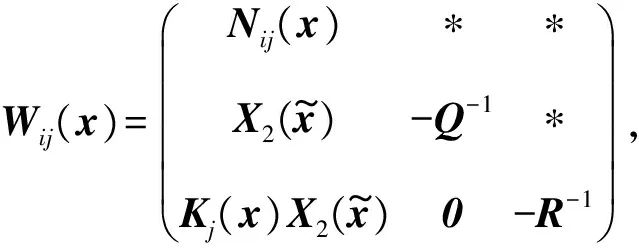
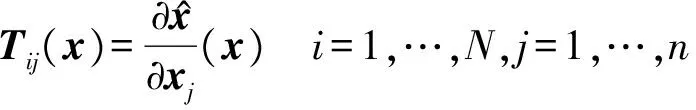
(12)

证明：考虑如下形式的候选多项式Lyapunov函数

(13)

沿式(5)的无外扰闭环模糊系统状态轨线，对V(x)求导，可得

(14)

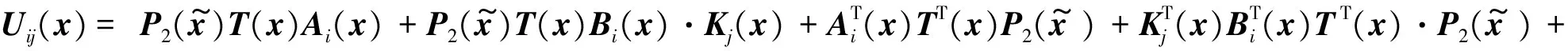
根据引理2，若条件式(10)和式(11)成立，则有

(15)

。

(16)

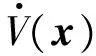
对式(16)两边分别从0到∞进行积分，并考虑当t→∞时，V(x(t))→ 0，可得

。

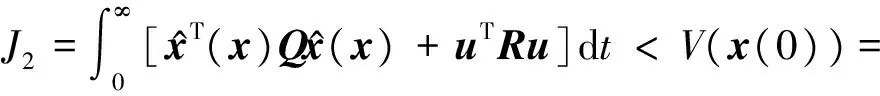
(17)

2.3 多项式模糊系统的H∞性能准则

下述定理给出了多项式模糊系统H∞性能判别方法。

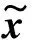
(18)

(19)

(20)

式中：Mij(x)=

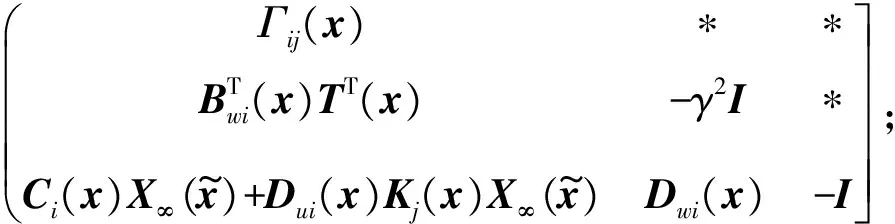
证明：采用与本文中的定理1以及文献[10]中的定理6类似的推导思路，可证得该定理。限于篇幅，略。

2.4 多项式模糊系统的混合H2/H∞性能准则

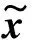
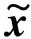
(21)

(22)

(23)

(24)

(25)

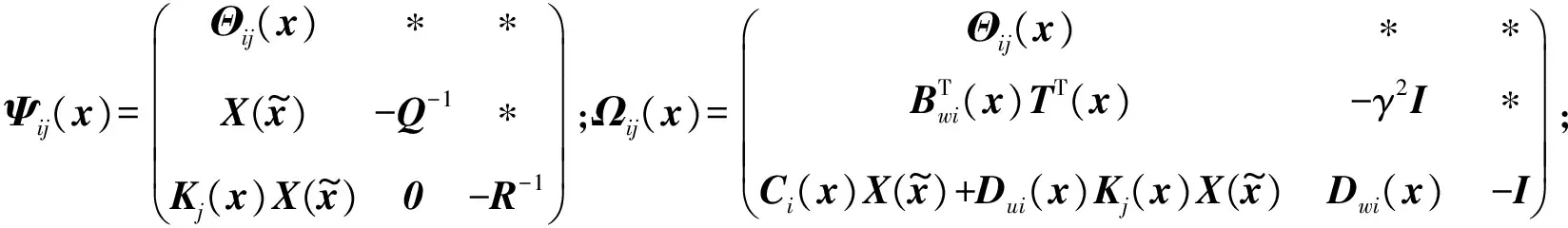
运用Matlab 平方和优化工具箱(SOSTOOLS)以及半定规划工具箱SeDuMi，可判定定理3中的所有条件式(21)～式(25)是否成立[11]。

3 多项式模糊系统混合H2/H∞控制器设计

本章在定理3的基础上，给出多项式模糊系统混合H2/H∞状态反馈模糊控制器的存在条件和设计方法。

3.1 混合H2/H∞状态反馈模糊控制器的存在条件

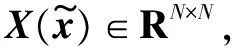
(26)

(27)

(28)

(29)

。

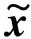
(30)

证明：令

。

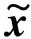
(31)

将式(31)代入式(22)～式 (25)，可得式(26)～式(29)。

3.2 混合H2/H∞状态反馈模糊控制器优化设计

引入变量λ，令

。

(32)

根据引理2和Schur补引理，如果

(33)

成立，式中,v16是与x不相关的向量，则有式(32)成立。

定理5给出了混合H2/H∞状态反馈模糊控制器的优化设计方法。

定理5对于式(3)的多项式模糊系统和给定的标量γ>0，如果以下的优化问题

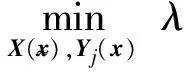
(34)

(35)

且式(5)的闭环多项式模糊系统H2性能的上界是λ*。

定理5中的式(34)优化问题是一个具有平方和约束条件的参数极小化问题，即平方和优化问题，可运用Matlab SOSTOOLS工具箱进行求解[11]。

4 算例仿真

考虑如下非线性系统

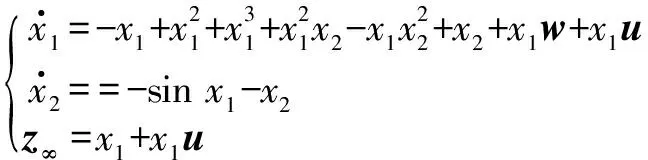
(36)

采用扇形非线性建模技术，建立描述式(36)的非线性系统多项式模糊模型[7]，即

(37)

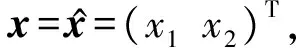
(38)

相应闭环模糊系统的H2性能的上界λ*=370.502 1，即由式(6)描述的系统H2性能指标满足J2<370.502 1。

为进一步验证本文方法的有效性，分别对本文提出的混合H2/H∞控制方法和文献[7]中的H∞控制方法进行仿真分析与比较。图1～图3分别给出了式(36)的非线性系统在H∞模糊控制器以及混合H2/H∞模糊控制器作用下的状态变化曲线和模糊控制输入量变化曲线。

由图1～图3可知，H∞模糊控制器以及混合H2/H∞模糊控制器均能使式(36)的非线性系统在干扰作用下保持稳定，具有良好的干扰抑制能力。

通过进一步计算可知，在H∞模糊控制器的作用下，式(36)非线性系统的实际H2性能为625.483 7；在混合H2/H∞模糊控制器的作用下，式(36)非线性系统的实际H2性能为326.670 2，从而表明与H∞控制相比，采用混合H2/H∞控制方法能够使系统获得更好的调节性能。

图1 系统状态x1(t)变化曲线Fig.1 Curve of system state x1(t)

图2 系统状态x2(t)变化曲线Fig.2 Curve of system state x2(t)

图3 模糊控制输入u(t)变化曲线Fig.3 Curve of fuzzy control input u(t)

5 结论

本文在分析多项式模糊系统H2性能和H∞性能的基础上，提出了一种具有公共Lyapunov矩阵的多项式模糊系统混合H2/H∞性能准则；进而，运用多项式Lyapunov函数与平方和优化技术，给出多项式模糊系统混合H2/H∞状态反馈模糊控制器存在条件，并将混合H2/H∞优化控制问题转化为一个具有多项式平方和约束的参数极小化问题，并给出了混合H2/H∞模糊控制器优化设计方法。

[1] TANAKA K,YOSHIDA H,OHTAKE H,et al.A sum of squares approach to stability analysis of polynomial fuzzy systems[C]//Proceedings of the American Control Conference,New York,2007:4071-4076.

[2] LAM H K,WU L,LAM J.Two-step stability analysis for general polynomial-fuzzy-model-based control systems [J].IEEE Transactions on Fuzzy Systems,2015,23(3):511-524.

[3] FURQON R,CHEN Y J,TANAKA M,et al.Stabilization analysis of single-input polynomial fuzzy systems using control Lyapunov Functions [C]//IEEE International Conference on Fuzzy Sytstems,Beijing,2014:907-912.

[4] TANAKA K,OHTAKE H,WANG H O.Guaranteed cost control of polynomial fuzzy systems via a sum of squares approach [J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2009,39(2):561-567.

[5] JIANG Y,ZHAO Y.H∞filtering of polynomial fuzzy systems with fading measurements[C]//Proceedings of the 33rd Chinese Control Conference,Nanjing,2014:4530-4533.

[6] HAN H,HIGAKI Y.Polynomial fuzzy controller design with disturbance observer using the SOS-based approach[J].IEEJ Transactions on Electrical and Electronic Engineering, 2015,10(4):458-464.

[7] 马清亮，邓会选，吕康文，等．基于平方和优化的多项式模糊系统H∞控制[J].电光与控制,2014,21(10):80-84.

[8] PARRILO P A.Structured semidefinite programs and semialgebraic geometry method in robustness and optimization[D].California：California Institute of Technology,2000.

[9] PRAJNA S，PAPACHRISTODOULOU A,WU F.Nonlinear control synthesis by sum of squares optimization:a Lyapunov-based approach[C]//Proceedings of the Asian Control Conference (ASCC),Melbourne,2004:157-165.

[10] LEE K P,JEUNG E T,PARK H B.Robust fuzzyH∞control for uncertain nonlinear systems via state feedback:an LMI approach[J].Fuzzy Sets and Systems,2001,120(1):120-134.

[11] PRAJNA S,PAPACHRISTODOULOU A,PARRILO P A.Introducing SOSTOOLS:a general purpose sum of squares programming solver[C]//Proceedings of the IEEE Conference on Decision and Control,Las Vegas,2002:741-746.

MixedH2/H∞ControlofPolynomialFuzzySystems

MA Qing-liang1, YANG Hai-yan2, WU Xu-guang2

(1.Department of Control Engineering,Rocket Force University of Engineering,Xi’an 710025,China; 2.School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China)

A mixedH2/H∞performance criterion with common Lyapunov matrix is proposed for polynomial fuzzy systems.Sufficient conditions for the existence of mixedH2/H∞state feedback fuzzy controller are derived based on the polynomial fuzzy Lyapunov function and Sum-of-Squares (SOS) decomposation technique.The optimalH2/H∞controller design approach is given by solving a parameter minimization problem with SOS constraints.

polynomial fuzzy system; mixedH2/H∞control; polynomial Lyapunov function; sum-of-squares optimization

马清亮,杨海燕,吴旭光.多项式模糊系统混合H2/H∞控制[J].电光与控制，2017，24(7)：1-6.MA Q L,YANG H Y,WU X G.MixedH2/H∞control of polynomial fuzzy systems[J].Electronics Optics & Control,2017,24(7):1-6.

TP13

A

10.3969/j.issn.1671-637X.2017.07.001

2016-06-28

2017-04-13

国家自然科学基金(61203007)

马清亮(1974 —),男,河南商水人，博士，副教授，研究方向为智能控制、非线性控制等。控制以及保性能控制等问题展开研究，并已有较多的研究成果[2-7]。