基于雷诺应力模型的高精度分离涡模拟方法∗

王圣业 王光学 董义道 邓小刚

1)(国防科学技术大学航天科学与工程学院,长沙 410073)2)(中山大学物理学院,广州 510275)

基于雷诺应力模型的高精度分离涡模拟方法∗

王圣业1)王光学2)董义道1)邓小刚1)†

1)(国防科学技术大学航天科学与工程学院,长沙 410073)2)(中山大学物理学院,广州 510275)

湍流流动,雷诺应力模型,分离涡模拟,加权紧致非线性格式

1 引 言

准确预测翼型和机翼在接近甚至超过失速迎角时的气动特性,已成为现代飞行器设计的重要方面.然而,对于高雷诺数大迎角条件下的分离流动,精确的计算流体力学(computational fluid dynamics,CFD)模拟仍十分困难[1].

任何流动模拟的结果都依赖于所代表的物理模型的准度以及求解相关方程的数值方法的精度[2].为了精确预测流动物理,主要是湍流,最好是直接求解所有尺度的湍流脉动甚至是最小尺度,即直接数值模拟;或求解大尺度湍流而模型化最小尺度,即大涡数值模拟(large eddy simulation,LES).然而,在真实飞行雷诺数下,即使附着边界层内的最大尺度脉动也会变得很小,这将使计算花费巨增而难以承担.因此,基于雷诺平均纳维-斯托克斯方程(Reynolds average Navier-Stokes,RANS)的湍流模型方法仍然是工业应用CFD的中坚力量[3].

混合雷诺平均/大涡模拟(hybrid RANS/LES)方法结合了大涡模拟方法在分离流动区域的高分辨率与雷诺平均方法在附着边界层中的高效率,在大迎角分离模拟中受到了广泛的关注[4−6].而在hybrid RANS/LES方法中,Spalart等[7]于1997年提出的分离涡模拟(detached eddy simulation,DES)方法由于其简单、高效等特点得到了广泛的发展和应用[8].然而,最初版本的DES方法基于一方程Spalart-Allmaras(SA)模型,在大规模分离流动支配的算例中表现良好,但对于由逆压梯度造成的初始尾缘分离等问题却很难准确估计.因此,为了更准确地模拟翼型和机翼的失速分离问题,尤其在失速迎角附近,DES的RANS部分需要采用更先进的湍流模型[9].2001年,Strelets[10]提出了基于二方程剪切压力传输(shear stress transport,SST)模型的DES方法,对翼型最大升力迎角附近时的分离问题有一定的提高.然而,由于线性涡粘模型自身的限制,其效果仍不理想.2006年,Greschner等[11,12]发展了基于EASM LLk-ε模型(一类非线性涡粘模型)的DES方法,并在串联圆柱-翼型算例中与传统k-ε-DES方法进行了对比.结果表明,EASM-DES方法能够更精细地分辨脱落涡结构,并且预测的气动力更接近试验值.但由于EASM模型仍基于Boussinesq假设框架,其对雷诺应力的求解仍然不直接,因此模拟效果对算例的敏感性较大.

雷诺应力模型(Reynolds stress model,RSM)是更高阶矩封闭的湍流模型,采用六个方程求解雷诺应力项和一个方程求解尺度约束变量(例如湍动能耗散率ε或比耗散率ω),能够直接估计雷诺应力各向异性、流线弯曲效应等[13].2011年,Probst等[9]基于ε型RSM模型,发展了εh-DES类方法,并在HGR-01翼型上取得了很好的结果.但由于ε型RSM模型鲁棒性较差,其适应性将不如ω型RSM模型[14].

近年来,德国宇航局的Eisfeld等[13,15,16]发展了一种鲁棒的RSM模型,Speziale-Sarkar-Gatski/Launder-Reece-Rodi(SSG/LRR)-ω模型,并在一系列复杂的航空分离流动中证明了其优势.美国航空航天局的Rumsey等[2]在湍流模型资源(turbulence modeling resource,TMR)网站上将SSG/LRR-ω模型设为最推荐的RSM,并开展了广泛的验证与确认工作.国内,董义道等[17]基于TMR网站,成功开展了SSG/LRR-ω模型的初步应用研究,但在应用过程中发现基于RANS方法的SSG/LRR-ω模型对翼型大迎角状态的模拟仍不理想.本文基于上述工作,在SSG/LRR-ω模型上发展了一类DES方法,并在典型航空算例(17◦,45◦及60◦迎角的NACA0012翼型;12◦迎角的NACA4412翼型;24.6◦迎角的钝前缘三角翼)中进行了验证.为了进行对比研究,本文还同时采用了传统基于线性涡粘模型的分离涡模拟方法,SST-DES方法.

对于DES方法,在RANS部分采用更先进的湍流模型,而在分离区LES部分则对数值精度的要求更高.相比传统二阶方法,高阶方法在采用较少计算花费获得更低误差方面具有更大的潜力[18−20].由于在计算效率和计算精度上的优势,高阶方法受到了广泛关注,并被推荐用于LES或hybrid RANS/LES方法中[21].本文中对RANS方程和模型方程的离散均采用了高阶精度的加权紧致非线性格式(weighted compact nonlinear scheme,WCNS)[22,23],并且在计算网格导数时采用了满足自由流保持的对称网格导数算法(symmetrical conservative metric method,SCMM)[24].

2 湍流模型

2.1 SSG/LRR-ω模型

对Navier-Stokes方程进行Favre平均后出现雷诺应力项.传统线性涡粘模型,如SA模型和SST模型,对雷诺应力项的求解均基于Boussinesq假设,而RSM则直接对其求解.

其中t,xk(k=1,2,3)分别为时间和空间坐标分量;,分别表示Favre平均的密度、速度分量和雷诺应力张量,而全雷诺应力不加特殊说明,下面出现的变量均为Favre平均后的量.(1)式右端第一项为生成项,可准确求解:

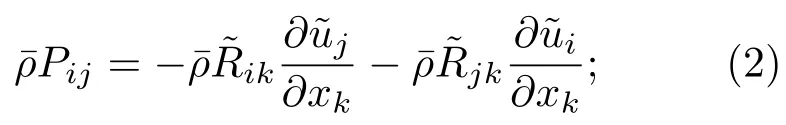
右端第三项为耗散项,

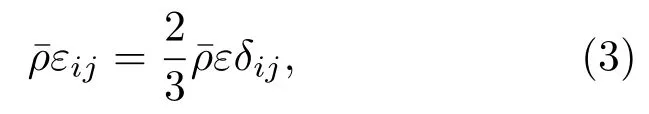
其中ε表示各向同性耗散率,需要通过额外的湍流尺度方程求解得到,δij为Kronecker符号.右端第四项为输运项,

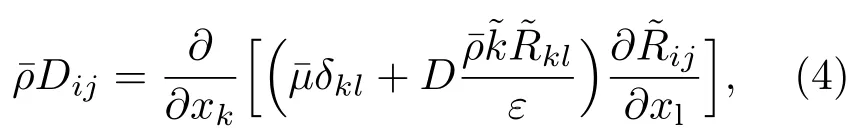
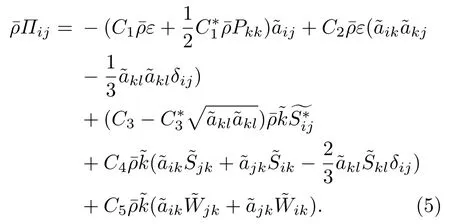
其中各向异性张量

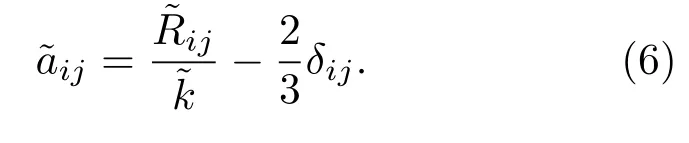
表1 SSG/LRR-ω模型封闭系数中SSG和LRR部分的贡献Table 1.Values of closure coefficients for the SSG and the LRR contributions to the SSG/LRR-ω redistribution term.

其他各项定义如下:

为了封闭上述模型,需要额外引入尺度方程,SSG/LRR-ω模型借鉴了Menter的思路,对ε方程和ω方程进行了混合[15]:

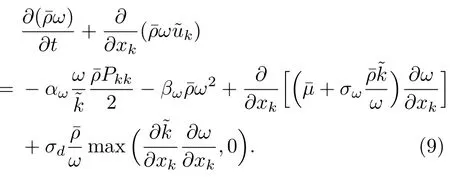
方程(9)的变量为比耗散率ω.各向同性耗散率通过下式计算:

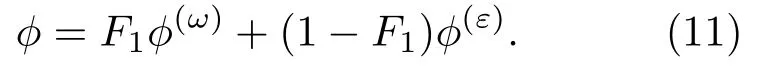
混合函数定义如下:

其中,dw为距壁面法向距离,其他系数具体见表2.

表2 ω方程系数中ε和ω部分的贡献Table 2.Values of coefficients of ω-equation corresponding to the ε and ω parts.

2.2 SSG/LRR-DES类方法

DES方法由Spalart等[7]提出,将LES方法和SA模型结合,并通过比较当地网格尺度与壁面距离实现两种方法的自动切换.其后,Strelet[10]借鉴Spalart的思想,通过比较当地网格尺度与湍流长度尺度,将DES方法引入SST模型.本文采用的SSG/LRR-ω模型与SST模型均为基于比耗散率ω的湍流模型,因此在构造SSG/LRR-DES方法时将主要借鉴SST-DES的构造思路.

首先定义网格长度尺度

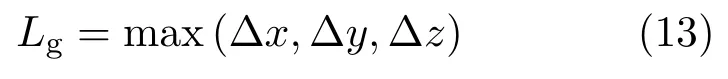
和湍流长度尺度

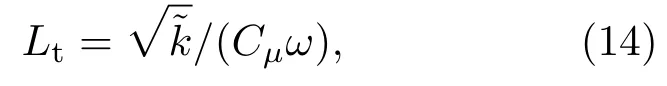
然后得到SSG/LRR-DES的限制器

对雷诺应力方程耗散项中的各向同性耗散率(10)式进行修正:

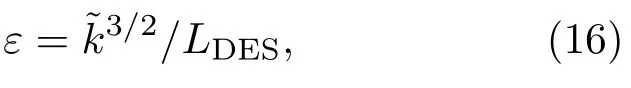
这里CDES为DES常数,通过Menter的混合函数(12)式得到

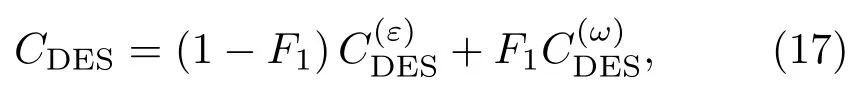
原始DES方法的限制器在复杂网格上处理RANS和LES的转换过程中过于生硬,会造成模化应力损耗(modeled stress depletion,MSD)等问题[8].2006年,Spalart等[26]借鉴Menter的SST模型构造思想,采用“延迟LES函数”改善了原始版本的MSD问题,发展出了延迟分离涡模拟(delayed DES,DDES)方法.2008年,Shur等[27]将DDES方法和壁面模型大涡模拟(wall-modeled LES,WMLES)方法结合,发展了强化延迟分离涡模拟(improved DDES,IDDES)方法,并在非定常分离流动中得到了广泛的应用.本文的计算中均采用IDDES形式,其构造过程如下.

首先采用WMLES中网格尺度的加权思想,定义新的IDDES限制器:

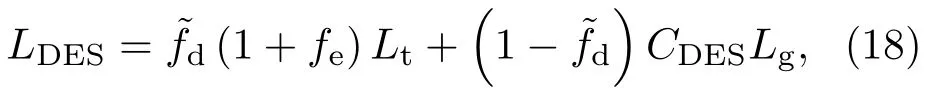
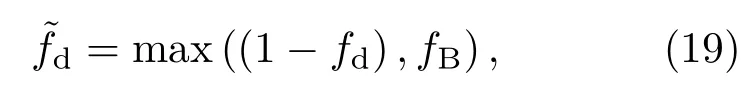
其中,fd为原DDES中的转换函数,fd=1−tanh(8rd)3,fB为原WMLES中的转换函数,fB=min(2exp(−9α2),1),这里α=0.25−dw/hmax;fe为壁面模拟的控制函数,其作用是保证在壁面附近网格分辨率满足LES要求时,忽略过渡区雷诺应力的影响.

其中fe1定义为

fe2定义为

(22)式中rd,rdt和rdl均与文献[27]中相同.

另外,在计算当地网格尺度时,Shur等[27]还引进了壁面距离的影响,新的Lg为

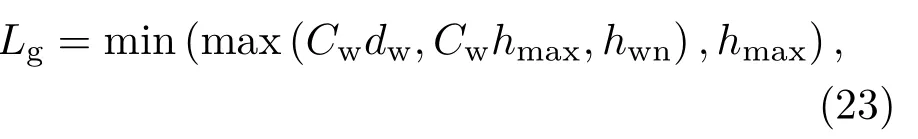
其中hmax=max(∆x,∆y,∆z),hwn为壁面垂直方向的网格步长.IDDES中的系数为Cw=0.15,ct=1.87和cl=5.0.

3 数值方法

3.1 高精度数值方法

WCNS格式由Deng等[22]在2000年提出.其后,不同学者[20,28,29]发展了多种形式的WCNS格式,并在广泛的流动问题中证明了该格式的优势.本文采用的是WCNS系列格式中一种典型的五阶显式离散格式WCNS-E-5[23].WCNS-E-5格式由于其低耗散、高鲁棒和优秀的自由流与涡保持特性,被广泛应用于各种实际流动问题的高精度数值模拟中.其中冈敦殿等[30]将WCNS-E-5格式应用于平板圆台突起物绕流的LES中,并和采用平面激光散射技术的试验结果进行了对比,证明了格式精细模拟湍流流动的可行性.

另外本文在计算网格导数及雅克比时,采用了满足几何守恒律的对称守恒网格导数算法[24],有利于提高高精度有限差分方法的鲁棒性并减小数值误差.本文中时间推进均采用子迭代步基于LU-SGS(lower-upper symmetric-Gauss-Seidal)方法的双时间步法.

3.2 对雷诺应力方程的高精度离散

较差的数值稳定性是限制RSM使用的障碍,尤其是结合高精度数值方法时.在迭代的过程中,雷诺应力项很可能不满足Schumann[31]提出的现实性限制.Chassaing等[32]提出一种鲁棒的隐式格式,依赖于使用当地双时间步技术和显式增强现实性限制.Yossef[33]发展了一种无条件正收敛隐式格式和一种现实性限制,保证了任意时间步内雷诺正应力项为正值.本文中,在雷诺应力方程的迭代过程中添加如下限制条件:

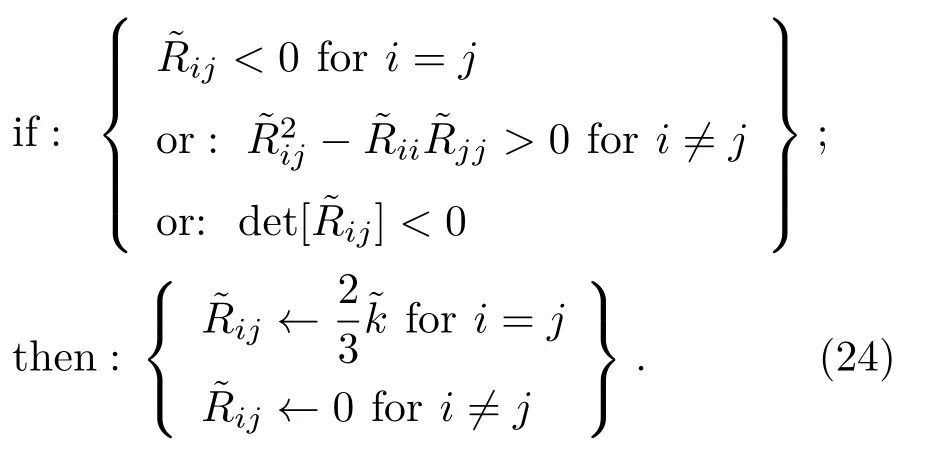
除了时间迭代方面,也应同时关注雷诺应力方程的空间离散.对于加权型有限差分格式,非线性权是影响数值稳定性的主要方面.需要指出的是,在对雷诺应力方程采用WCNS类格式离散时,加权公式中的小量εIS应取为10−18,而非文献[23]中对Navier-Stokes方程离散时的10−6.

4 计算结果

4.1 NACA0012翼型大迎角气动特性模拟

NACA0012翼型大迎角分离算例是推动DES发展的经典算例.2001年,Strelets等[7]在提出SST-DES类方法时,就在该算例上与原始的SADES类方法进行了对比,但发现并无本质的差异.2016年,Yang和Zha[34]结合高精度WENO(weighted essentially nonoscillatory)格式,采用改进的SA-IDDES方法对该算例进行了模拟,但发现在中等迎角下SA-IDDES方法还没有SA-URANS方法准确.本文为了更好地对SSG/LRR-IDDES方法进行对比研究,计算条件和网格均参考Yang和Zha的工作[34],并同时采用了SST-IDDES方法.

图1 NACA0012翼型三维粗糙网格Fig.1.Three-dimensional coarse grid of the NACA0012 airfoil.

NACA0012翼型基于弦长c的雷诺数为1.3×106,基于自由流速度的马赫数为0.5.在0◦—90◦迎角范围内,选取17◦(大范围边界层分离),45◦和60◦(大规模脱体分离)三个典型状态进行模拟.由于该算例在高雷诺数(Re>1.0×105)下受雷诺数影响很小,因此升力和阻力系数的参考值选取Re=2.0×106的试验值[34,35].本文计算采用粗和密两套O型网格,网格单元数分别为192×102×30和288×102×30.第一层网格小于1;远场长度约为100c;展向长度为1.0c.图1为NACA0012翼型三维网格示意图.时间推进采用双时间步方法,周期为T=c/U∞,时间步长0.01T.时间平均统计从50T时开始,持续50T.

图2展示了3个典型迎角下统计时间的平均升、阻力系数.在17◦迎角时,翼型处于失速状态,所有方法得到的阻力系数相近且与试验吻合较好;但对于升力系数,SSG/LRR-IDDES在粗网格上略低于试验值,而在密网格上与试验值吻合很好;而其他方法均明显高于试验值.Yang和Zha[34]在17◦迎角的计算中,得出了WENO+SA-IDDES结果明显差于WENO+SA-URANS的现象,但并未给出解释.而本文采用的线性涡粘模型、SST模型并未出现该现象.在45◦和60◦迎角时,翼型处于过失速状态,所有IDDES方法的结果均明显优于URANS方法.同时对比两类URANS方法,SSG/LRR-ω模型略优于SST模型,而该现象与相关湍流模型在分离涡处对雷诺应力预测的能力有关.

图3展示了17◦迎角时升、阻力系数在100T内的变化过程,其中AoA表示迎角.可以看到在25T后,SST-URANS和SSG/LRR-URANS得到的升、阻力系数出现类似简谐振荡的发展过程.而SSTIDDES和SSG/LRR-IDDES方法得到的升、阻力系数均为无周期振荡,表明其均能够描述分离湍流的随机性.对比试验值,SST-IDDES得到的升力系数明显偏高,并且随网格加密无明显改善,反映了基于线性涡粘模型的DES方法在翼型最大升力迎角附近模拟的局限.

经典的涡拉伸原理[36]表明,三维性是湍流最本质的特性之一.图4给出的粗网格上100T时刻Q判据为0的三维等值面图中,SST-URANS预测的涡脱落过程明显为二维过程;SSG/LRRURANS能够预测出上翼面附近较小尺度的涡,但整个涡脱落过程仍未表现出明显的三维性;而SST-IDDES和SSG/LRR-IDDES均得到了高度混乱的三维涡结构,但SSG/LRR-IDDES对前缘涡拉伸-弯曲-破裂的过程则模拟的更为精细.

图5对比了不同方法在粗网格上100T时刻0.5展长处的展向速度,其中SST-URANS得到的展向流动十分微弱,也印证了其为二维涡脱落过程;SSG/LRR-URANS得到的展向流动稍强于SSTURANS,但也未表现出明显的三维性;而SSTIDDES和SSG/LRR-IDDES均预测出了明显的展向流动.

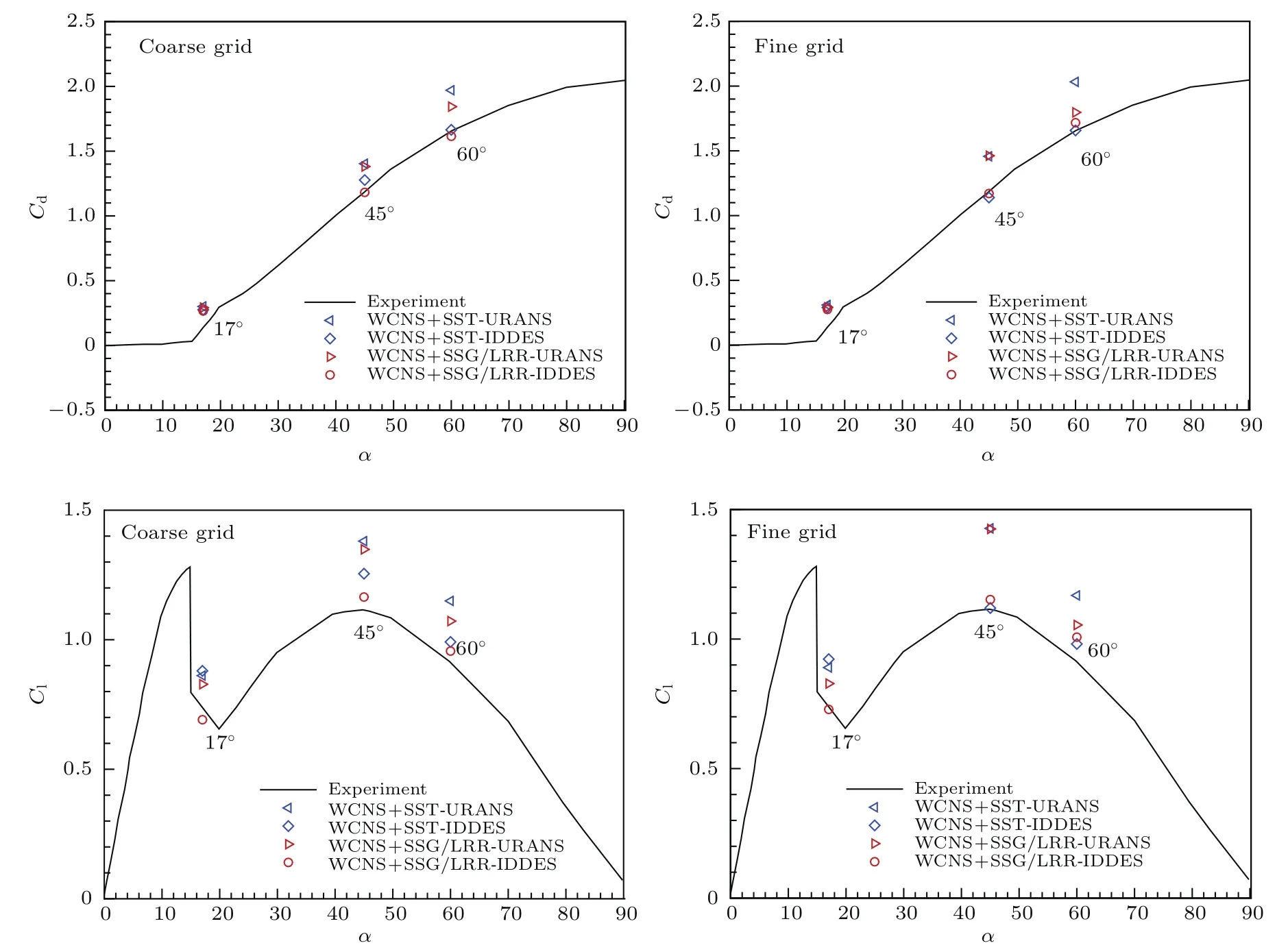
图2 (网刊彩色)0◦—90◦范围内3个典型迎角下的升阻力结果对比Fig.2.(color online)Comparisons of lift and drag coefficients at 3 typical attack angles of among 0◦–90◦.

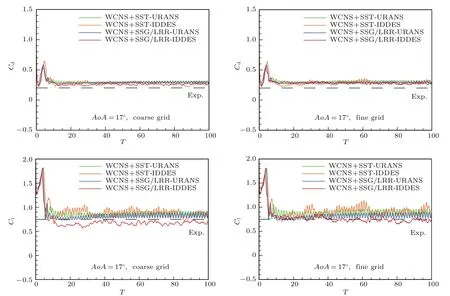
图3 (网刊彩色)17◦迎角时升、阻力系数变化过程Fig.3.(color online)Lift and drag coe ff cient history at attack angle of 17◦.

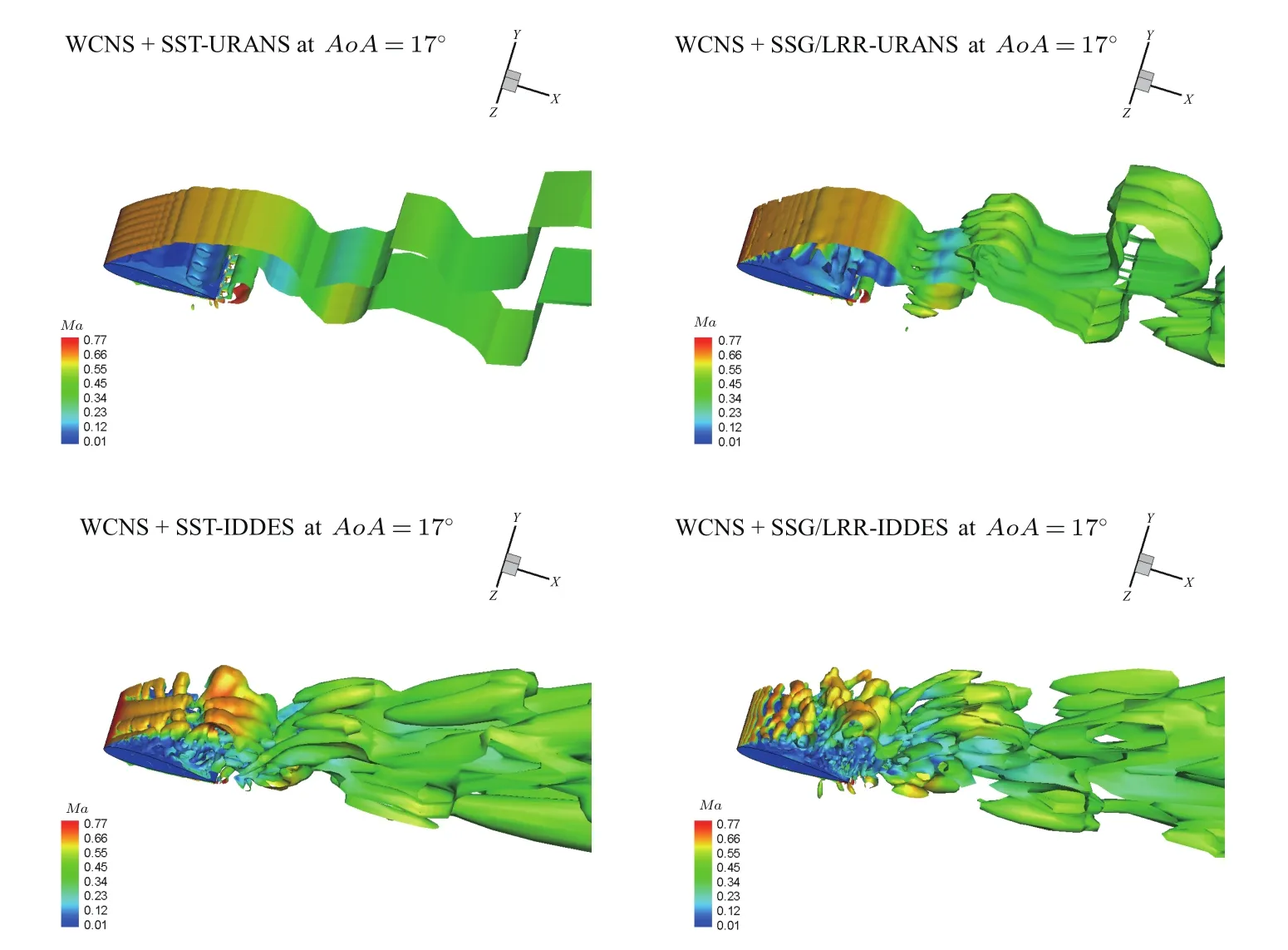
图4 (网刊彩色)17◦迎角下100T时刻Q判据为0的等值面图,颜色由马赫数标识Fig.4.(color online)Iso-surface of the Q-criterion=0 at 100T and attack angle of 17◦,colored by Mach number.

图5 (网刊彩色)17◦迎角下100T时刻,0.5展长处展向速度云图Fig.5.(color online)Spanwise velocity contours of 50%span at 100T and attack angle of 17◦.

图6展示了45◦迎角时升、阻力系数在100T内的变化过程.可以看到在25T后,SST-URANS得到的升、阻力系数出现类似简谐振荡的发展过程,而SSG/LRR-URANS并未得到有规律的简谐振荡过程,这与RSM能够估计雷诺应力的各向异性有关.而SST-IDDES和SSG/LRR-IDDES方法得到的升、阻力系数均在试验值附近无规律振荡.

图6 (网刊彩色)45◦迎角时升、阻力系数变化过程Fig.6.(color online)Lift and drag coe ff cient history at attack angle of 45◦.

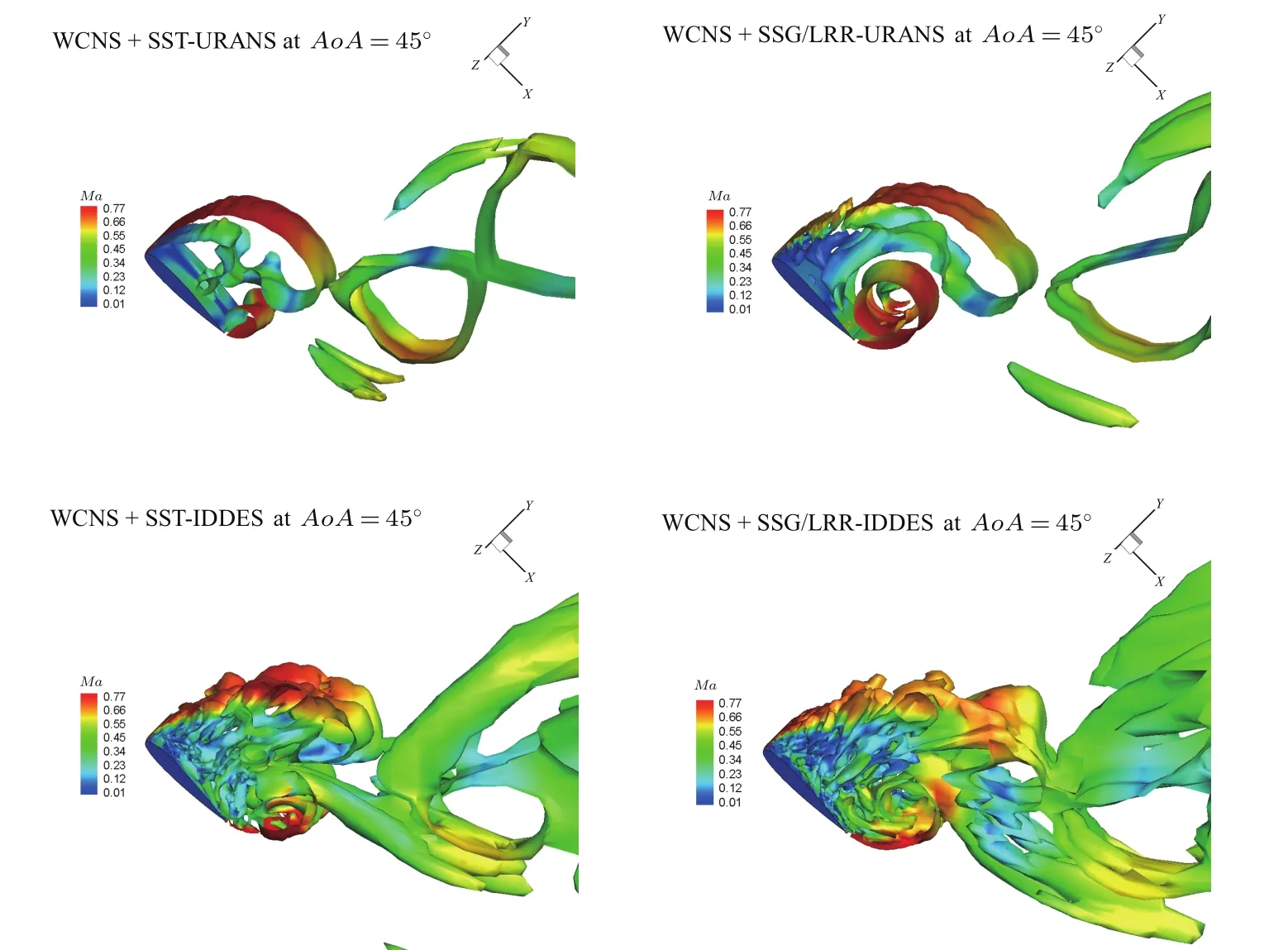
图7 (网刊彩色)45◦迎角下100T时刻Q判据为0的等值面图,颜色由马赫数标识Fig.7.(color online)Iso-surface of the Q-criterion=0 at 100T and attack angle of 45◦,colored by Mach number.

来流流过机翼后形成脱体的分离湍流,并将产生明显的展向流动.图7给出了粗网格上45◦迎角,100T时刻,Q判据为0的三维等值面图.SSTURANS仅预测出了大尺度的展向涡,其涡脱落过程仍为二维过程;SSG/LRR-URANS能够预测出少量的流向和法向涡,但仍未表现出明显的三维过程;而SST-IDDES和SSG/LRR-IDDES得到了高度混乱的大小涡结构,预测出了明显的三维效应. 图8对比了不同方法在粗网格上100T时刻0.5展长处的展向速度,更加清晰地表明各方法对于分离湍流的预测能力. 这也是图3中SST-IDDES和SSG/LRR-IDDES的结果优于SSG/LRR-URANS、更优于SST-URANS的原因.

图8 (网刊彩色)45◦迎角下100T时刻,0.5展长处展向速度云图Fig.8.(color online)Spanwise velocity contours of 50%span at 100T and attack angle of 45◦.

图9 (网刊彩色)60◦迎角时升、阻力系数收敛过程Fig.9.(color online)Lift and drag coe ff cient history at attack angle of 60◦.

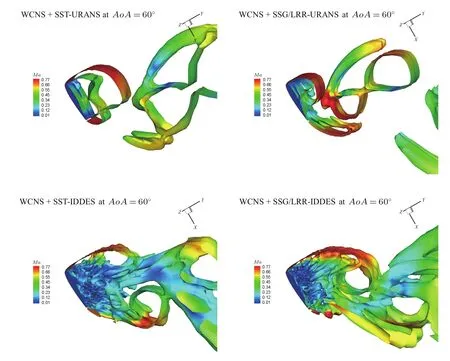
图10 (网刊彩色)60◦迎角下100T时刻Q判据为0的等值面图,颜色由马赫数标识Fig.10.(color online)Iso-surface of the Q-criterion=0 at 100T and attack angle of 60◦,colored by Mach number.

图11 (网刊彩色)60◦迎角下100T时刻,0.5展长处展向速度云图Fig.11.(color online)Spanwise velocity contours of 50%span at 100T and attack angle of 60◦.

图9展示了60◦迎角时升、阻力系数的变化过程.与45◦迎角时的结果类似,在25T后,SSTURANS得到的升、阻力系数出现明显的周期性;而SSG/LRR-URANS，SST-IDDES和SSG/LRRIDDES呈现出无规律振荡,但SSG/LRR-URANS得到的升、阻力系数平均值明显高于试验值.图10给出了60◦迎角100T时刻下,Q判据为0的三维等值面图.SST-URANS预测的涡脱落过程仍为二维过程;SSG/LRR-URANS得到的结果也仍未表现出明显的三维过程;而SST-IDDES和SSG/LRRIDDES得到了高度混乱的大小涡结构,预测出了明显的三维效应.图11给出了60◦迎角100T时刻0.5展长处的展向速度云图,结果也与45◦迎角时类似.

4.2 NACA4412翼型尾缘分离模拟

NACA4412翼型是经典的低速湍流验证算例[37],有多种条件下的详细试验数据进行对比.本文选择的是以Wadcock[38]实施的最大升力构型(12◦迎角)试验为参考的算例.试验条件为:翼型弦长0.9 m,雷诺数1.64×106,自由流速度29.1 m/s以及马赫数0.085.该条件下翼型尾缘开始出现分离,对任何hybrid RANS/LES方法都是巨大的挑战[39].

本文计算的条件设置与试验相同.采用粗和密两套O型网格,展向拉伸0.1 m,网格单元数分别为169×123×30和249×123×30.第一层网格均小于1.图12为NACA4412翼型三维网格示意图.时间推进采用双时间步法,周期为T=c/U∞,时间步长0.01T.时间平均统计从40T时开始,持续40T.

表3列出了平均升力系数和分离位置的计算值与试验值.可以看到,SST-URANS、SSG/LRRURANS和SST-IDDES得到的结果均与试验值偏差较大,并且随着网格加密未有改善. 而SSG/LRR-IDDES的结果与试验吻合较好.

图12 NACA4412翼型三维粗网格Fig.12.Three-dimensional coarse grid of the NACA4412 airfoil.

表3 NACA4412翼型平均升力系数和分离位置的计算值与试验值对比Table 3.Comparation of computional results of lift coefficient and location of separation for NACA4412 airfoil case.

图13 (网刊彩色)NACA4412翼型80T时刻,Q判据为0等值面图,颜色由马赫数标识Fig.13.(color online)Iso-surface of the Q-criterion=0 at 80T for NACA4412 airfoil case,colored by Mach number.

图13给出了粗网格上80T时刻Q判据为0的等值面图.在翼型尾缘处,流动开始分离并产生湍流尾迹涡.SSG/LRR-IDDES成功模拟了该过程,并且分离位置与试验吻合.图14给出了该网格上得到的平均压力系数分布和试验值的对比.SSG/LRR-IDDES在前缘得到的吸力值明显低于另三种方法,并且与试验值更接近,这也是其得到更准确升力系数的原因.在翼型尾缘处,由于SSG/LRR-IDDES成功模拟了尾迹涡结构,其得到的压力系数也更接近试验值.图15展示了翼型尾缘(x/c=0.952)和尾迹(x/c=1.282)两个典型站位处的流向速度分布对比.在x/c=0.952处,SSG/LRR-IDDES成功捕捉到了逆向速度,计算结果与试验吻合.表明SSG/LRR-IDDES能在边界层附近更好地感受逆压梯度的影响,对于弱非定常流动较传统SST-IDDES方法有一定提高.而仅采用URANS方式会引入过多湍流黏性,使弱非定常运动的发展受到抑制.在x/c=1.282处,SSG/LRR-IDDES得到的流向速度略大于试验值,且与其他三种方法无明显区别.

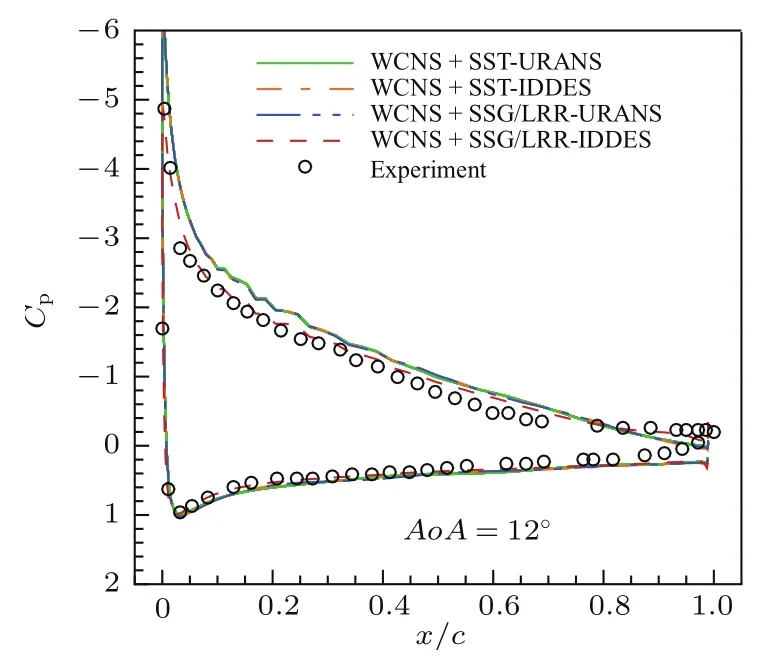
图14 (网刊彩色)NACA4412翼型表面压力系数分布Fig.14.(color online)Distribution of pressure coefficient on the surface of NACA4412 airfoil.

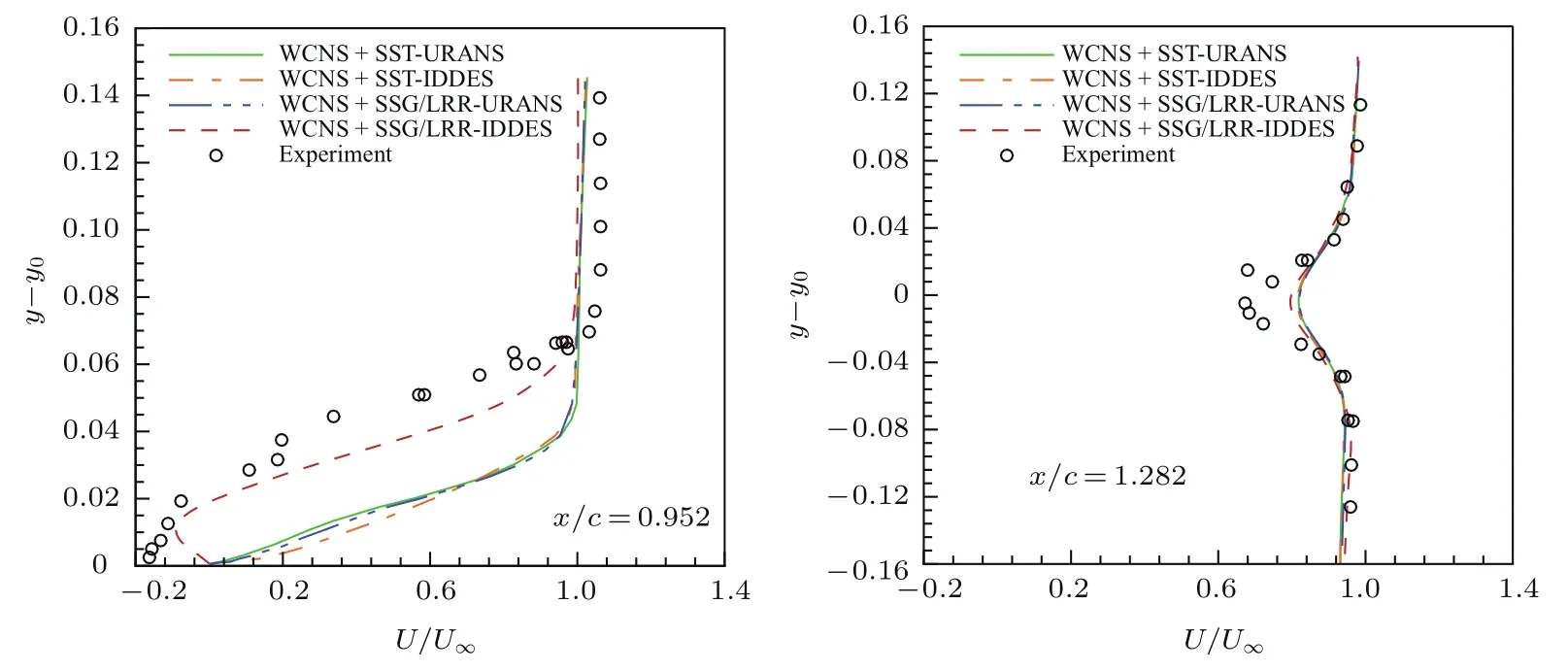
图15 (网刊彩色)NACA4412翼型流向速度分布比较Fig.15.(color online)Comparison of streamwise velocity pro files for NACA4412 airfoil.

4.3 钝前缘三角翼涡破裂模拟

现代战斗机和导弹多采用三角翼布局,以获得良好的飞行品质和机动性能.然而在大迎角下,三角翼会产生涡破裂现象对气动特性造成影响.本文采用的计算模型为65◦后掠三角翼,是NASA Langley中心为研究该外形的雷诺数、马赫数影响而完成的试验模型[40].该模型分为四部分:前缘、平板部分、后缘及整流罩.前缘部分提供4种可替换外形,本文选用中等半径钝前缘外形.来流条件为:Ma=0.85,Re=6×106.迎角选择24.6◦,为涡破裂现象发生的临界迎角.

本文采用的计算网格自主生成,网格单元数约6百万,网格结构为多块对接网格.图16给出了三角翼的表面网格.网格拓扑采用C-H型,以避免翼尖奇性轴的产生.计算区域的远场边界取为50倍根弦长.壁面的第一排网格达到了10−6弦长,网格在背风区和剪切层附近均进行了适当的加密,以保证分离区、附面层内和剪切层的数值模拟精度.时间推进采用双时间步法,周期为T=cref/U∞,其中cref为参考气动弦长,时间步长取0.01T.时间平均统计从10T时开始,持续20T.

图16 钝前缘三角翼计算网格Fig.16. Computational mesh for the blunt-edge deltawing.

图17展示了钝前缘三角翼不同站位处压力分布与试验[41]的对比,其中η=2z/bl,bl为当地展长,cr为翼根弦长.回顾钝前缘三角翼分离的基本特性.相比传统尖前缘,钝前缘三角翼在前缘处有转捩过程[42],但本文计算的马赫数较高,迎角也较大,因此转捩过程很短,分离涡为全湍流状态.主涡旋转产生展向流动,在旋涡下部、三角翼的上翼面加速,出现负压力峰值,该点沿展向到翼边缘是逆压梯度,将诱导边界层分离,产生二次分离和二次旋涡,在主涡负压力峰值外侧又出现二次负压力峰值.观察x/cr=0.4站位的压力分布,SST-IDDES,SSG/LRR-URANS和SSG/LRR-IDDES均成功捕捉到了二次涡结构,而其中SSG/LRR-IDDES与试验值吻合最好.

当迎角大到一定程度时,主涡开始破裂.本文选择的24.6◦迎角,为涡破裂现象发生的临界迎角,而x/cr=0.6是该迎角下涡破裂发生前的临界站位.因此该站位的模拟对CFD方法是个挑战.观察本文计算值与试验值的对比,四种方法均产生了不同程度的偏差.其中SSG/LRR-IDDES在吸力峰处与试验吻合很好,但在翼根处吻合较差.x/cr=0.6站位的翼根处临近整流罩头部(存在速度驻点),压力系数由负值迅速变为接近1从而形成较大的压力梯度,因此给数值模拟带来很大困难.

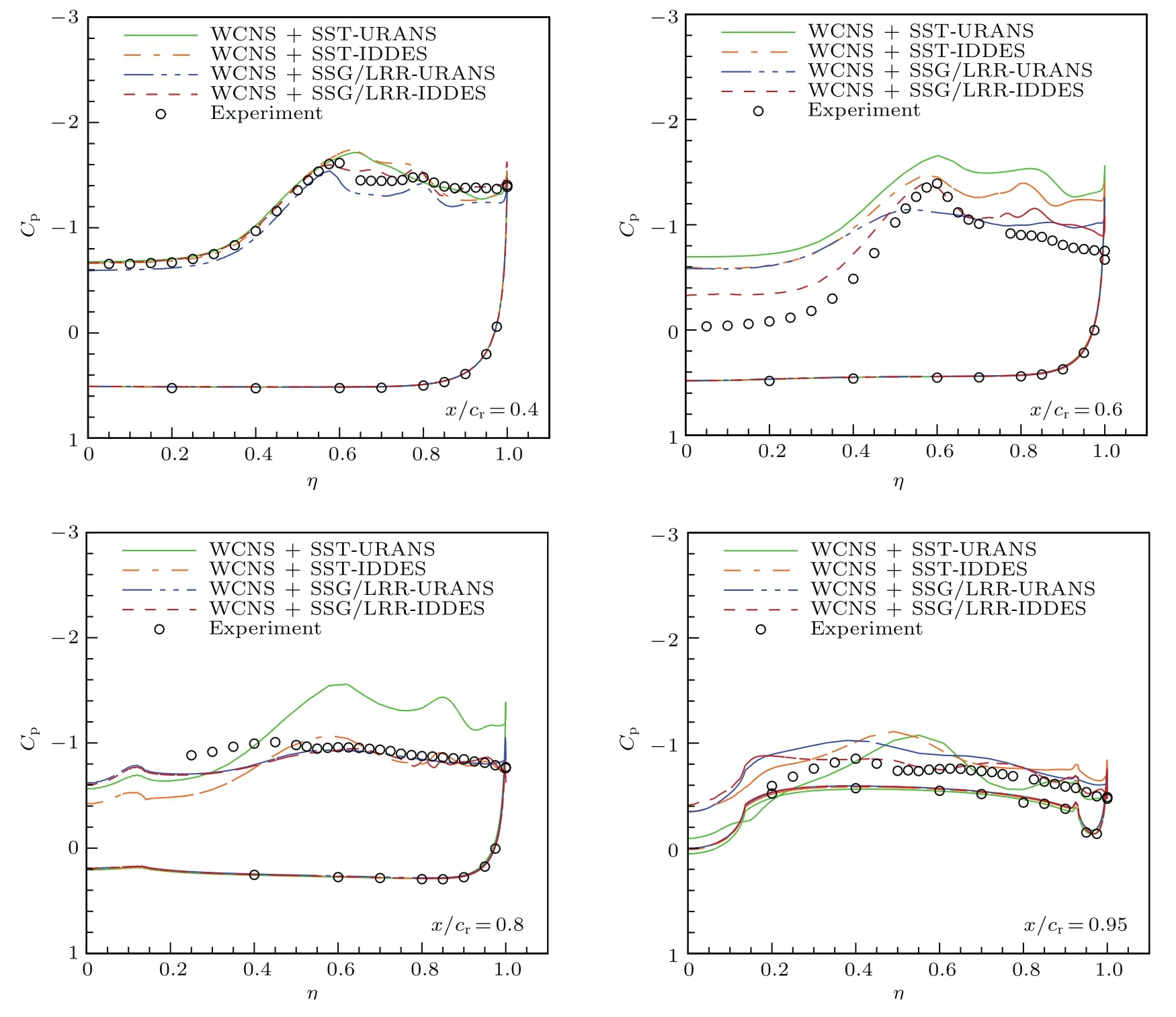
图17 (网刊彩色)钝前缘三角翼不同站位处压力分布对比Fig.17.(color online)Comparisons of surface pressure with experiments for blunt-edge deltawing at typical stations.

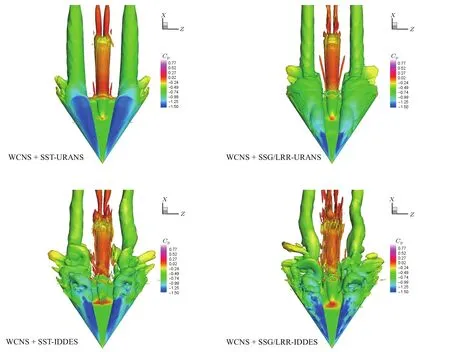
图18 (网刊彩色)三角翼20T时刻Q判据等值面图,颜色由压力系数标识Fig.18.(color online)Iso-surface of the Q-criterion at 20T for deltawing case,colored by pressure coefficient.

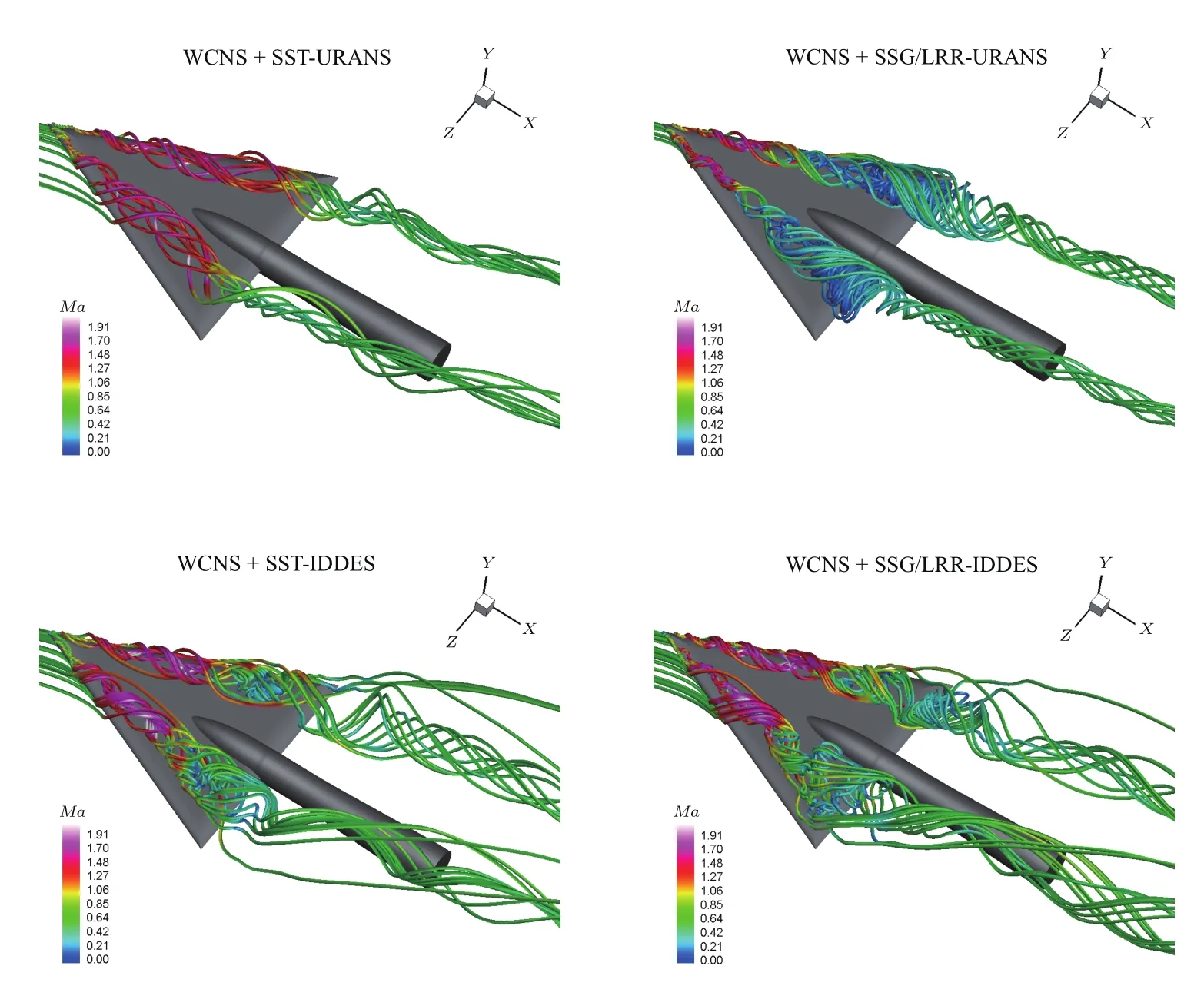
图19 (网刊彩色)三角翼20T时刻流线图,颜色由马赫数标识Fig.19.(color online)Streamlines at 20T for deltawing case,colored by Mach number.

在x/cr=0.8处,涡破裂已发生,上翼面吸力峰消失.SST-IDDES,SSG/LRR-URANS和SSG/LRR-IDDES均成功地预测了该现象,而SST-URANS仍得到了主涡及二次涡结构.结合其他站位上SST-URANS得到的压力分布,可以看出在24.6◦迎角下,其并未预测到涡破裂现象,即推迟了涡破裂的发生.而该现象的产生明显由SSTURANS在分离区过大的湍流黏性导致.由于来流为跨声速,前缘涡引起的上翼面流动加速,形成了局部超音速区域并产生了激波.对于跨声速流动,Rumsey[14]在ONERO M6机翼和NASA CRM翼身组合构型中均表明,SSG/LRR-ω模型能更好地预测激波附近雷诺应力的剧烈变化,对激波诱导分离的模拟能力明显优于SST等涡粘模型.本文发展的SSG/LRR-IDDES方法继承了RSM的优势,在非定常区(x/cr=0.8和x/cr=0.95)得到了优于SST-IDDES方法的结果.

图18和图19分别展示了20T时刻三角翼Q判据等值面图和流线图.SST-URANS得到的仍为定常状态的前缘分离涡,在24.6◦迎角时未发生涡破裂.SSG/LRR-URANS虽然预测到了涡破裂,但涡破裂后的流动未表现出明显的非定常特性.表明对涡破裂后形成的非定常运动,需采用诸如DES,LES等的尺度模拟方法.SST-IDDES和SSG/LRR-IDDES均较好地模拟了涡破裂后的非定常流动状态,但就精细度而言,SSG/LRRIDDES要更为优秀.

5 结 论

本文借鉴SST-IDDES方法的构造方式,在SSG/LRR-ωRSM上发展了SSG/LRR-IDDES分离涡模拟方法.通过结合高精度WCNS格式在NACA系列翼型及钝前缘三角翼算例上进行了验证,并和传统SST-IDDES方法以及SSG/LRRURANS和SST-URANS方法进行了对比.

为说明SSG/LRR-IDDES方法在翼型大迎角气动力模拟方面的提升,选取NACA0012翼型17◦,45◦和60◦三个典型状态进行模拟.在17◦迎角时,翼型边界层分离扩大到前缘附近,升力系数接近最小.此时,采用SST-URANS和SSG/LRR-URANS均会过高估计升力,而采用传统基于线性涡粘模型的SST-IDDES方法也并未明显改善.这说明对于传统基于线性涡粘模型的IDDES方法,由于边界层附近RANS部分本身对逆压梯度引起的分离的模拟能力较差,使得整个方法较URANS并无明显提高.而基于RSM,可以更准确地估计逆压梯度区的雷诺应力变化,使得结合IDDES时得到了很好的结果.到45◦和60◦迎角时,翼型产生大范围脱体涡,升力系数回升.此状态是传统IDDES方法模拟的优势方面,而SSG/LRR-IDDES也继承了该特性,并较SSG/LRR-URANS有较大提高.

为说明SSG/LRR-IDDES方法在翼型最大升力迎角附近的模拟能力,选取NACA4412翼型12◦状态进行模拟.此时,翼型尾迹由于逆压梯度影响开始分离并产生湍流尾迹涡.采用SST-URANS和SSG/LRR-URANS均会过高估计升力,并延迟了尾迹分离;而采用SST-IDDES也未明显改善.但是采用SSG/LRR-IDDES方法给出了与试验吻合很好的气动力特性和准确的分离过程,表明该方法对模拟翼型失速迎角附近特性的能力提高.

为进一步说明SSG/LRR-IDDES方法在三维机翼失速迎角附近的模拟能力,选取钝前缘三角翼24.6◦状态进行模拟.该迎角下,三角翼主涡由于激波诱导的影响,在x/cr=0.6站位后发生非定常涡破裂现象.采用SST-URANS方法无法成功预测涡破裂现象;而采用SSG/LRR-URANS方法虽然预测到了涡破裂,但涡破裂后的流动未表现出明显的非定常特性.采用SST-IDDES方法和SSG/LRR-IDDES方法均较好地模拟了涡破裂后的非定常流动状态,但在表面压力分布、流场精细度等方面,SSG/LRR-IDDES方法更加优秀.

另外,本文采用的WCNS-E-5格式能够在粗糙网格上获得较高的保真度,体现了高精度数值方法在模拟分离流动中的效率优势.但在加密网格计算时,也出现了网格收敛性差的现象,如NACA0012翼型60◦迎角时,SSG/LRR-IDDES在粗网格下得到的平均气动力系数略优于密网格.该现象的产生与IDDES方法基于网格长度尺度来调整湍流黏性有关,也是DES类方法需要克服的问题之一[8].下一步,将继续结合高精度格式对SSG/LRR-IDDES方法在更广泛的流动中进行验证并提高网格收敛性.

[1]Slotnick J,Khodadoust A,Alonso J,Darmofal D,Gropp W,Lurie E,Mavriplis D 2014CFD Vision 2030 Study:A Path to Revolutionary Computational Aerosciences(Washington,DC:Langley Research Center,NASA)Tech.Rep.NASA/CR-2014-218178

[2]Eisfeld B,Rumsey C,Togiti V 2016AIAA J.54 1524

[3]Rumsey C 201452nd Aerospace Sciences MeetingNational Harbor,Maryland,January 13–17,2014 AIAA 2014-0201

[4]Tucker P 2006Int.J.Numer.Meth.Fluids51 261

[5]Richez F,Pape A,Costes M 2015AIAA J.53 3157

[6]Xu G,Jiang X,Liu G 2016Acta Mech.Sin.32 588

[7]Spalart P,Jou W H,Strelets M,Allmaras S 1997Comments on the Feasibility of LES for Wings,and on Hybrid RANS/LES Approach(Columbus:Greyden Press)

[8]Spalart P 2009Annu.Rev.Fluid Mech.41 181

[9]Probst A,Radespiel R,Knopp T 201120st AIAA Computational Fluid Dynamics ConferenceHonolulu,Hawaii,June 27–30,2011 AIAA 2011-3206

[10]Strelets M 200139th AIAA Aerospace Sciences Meeting and ExhibitReno,NV,8-11 January 2001,AIAA 2001-0879

[11]Greschner B,Thiele F,Gurr A,Casalino D,Jacob M200612th AIAA/CEAS Aeroacoustics ConferenceCambridge,Massachusetts,May 8–10,2006 AIAA 2006-2628

[12]Greschner B,Thiele F,Jacob M,Casalino D 2008Comput.Fluids37 402

[13]Cécora R D,Radespiel R,Eisfeld B,Probst A 2015AIAA J.53 739

[14]Rumsey C 2015 in Eisfeld B(ed.)Differential ReynoldsStress Modeling for Separating Flows in Industrial Aerodynamics(Springer Tracts Mechanical Engineering)p19

[15]Eisfeld B,Brodersen O 200523rd AIAA Applied Aerodynamics ConferenceToronto,Ontario Canada,June 6–9,2005 AIAA 2005-4727

[16]Togiti V,Eisfeld B,Brodersen O 2014J.Aircraft51 1331

[17]Dong Y D,Wang D F,Wang G X,Deng X G 2016J.National Univ.Defense Technol.38 46(in Chinese)[董义道,王东方,王光学,邓小刚2016国防科技大学学报38 46]

[18]Shu C 2003Int.J.Comput.Fluid D17 107

[19]Wang Z,Fidkowski K,Abgrall R,Bassi F,Caraeni D,Cary A,Deconinck H,Hartmann R,Hillewaert K,Huynh H,Kroll N,May G,Persson P O,van Leer B,Visbal M 2013Int.J.Numer.Meth.Fluids72 811

[20]Wang S,Deng X,Wang G,Xu D,Wang D 2016Int.J.Comput.Fluid D30 469

[21]Georgiadis N,Rizzetta D,Fureby C 2010AIAA J.48 1772

[22]Deng X,Zhang H 2000J.Comput.Phys.165 22

[23]Deng X,Liu X,Mao M,Zhang H 200517th AIAA Computational Fluid Dynamics ConferenceToronto,Ontario Canada,June 6–9,2005 AIAA 2005-5246

[24]Deng X,Mao M,Tu G,Liu H,Zhang H 2011J.Comput.Phys.230 1100

[25]Bellot G,Corrsin S 1971J.Fluid Mech.48 273

[26]Spalart P,Deck S,Shur M,Squires K,Strelets M,Travin A 2006Theor.Comput.Fluid Dyn.20 181

[27]Shur M,Spalart P,Strelets M,Travin A 2008Int.J.Heat Fluid Fl.29 1638

[28]Nonomura T,Fujii K 2009J.Comput.Phys.228 3533

[29]Liu H,Ma Y,Yan Z,Mao M,Deng X 20148th International Conference on Computational Fluid DynamicsChengdu,China,July 14–18,2014 ICCFD8-2014-0082

[30]Gang D D,Yi S H,Zhao Y F 2015Acta Phys.Sin.64 054705(in Chinese)[冈敦殿,易仕和,赵云飞2015物理学报64 054705]

[31]Schumann U 1977Phys.Fluids20 721

[32]Chassaing J,Gerolymos G,Vallet I 2003AIAA J.41 763

[33]Yossef Y 2014J.Comput.Phys.276 635

[34]Yang Y,Zha G 201646th AIAA Fluid Dynamics ConferenceWashington,D.C.,USA,June 13–17,2016 AIAA 2016-3185

[35]Shur M,Spalart P,Strelets M,Travin A 1999Proceedings of the 4th International Symposium on Engineering Turbulence Modelling and MeasurementsCorsica,France,May 24–26,1999 p669

[36]Chen M Z 2002Fundamentals of Viscous Fliud Dynamics(Beijing:Higher Education Press)p239(in Chinese)[陈懋章 2002 粘性流体动力学基础 (北京:高等教育出版社)第239页]

[37]Chen Y,Guo L D,Peng Q,Chen Z Q,Liu W H 2015Acta Phys.Sin.64 134701(in Chinese)[陈勇,郭隆德,彭强,陈志强,刘卫红2015物理学报64 134701]

[38]Wadcock A 1987Investigation of Low Speed Turbulent Scparatcd Flow Around Airfoils(Washington,DC:Ames Research Center,NASA)Tech.Rep.NASA-CR-177450

[39]Roy R,Stoellinger M 201553rd AIAA Aerospace Sciences MeetingKissimmee,Florida,January 5–9,2015 AIAA 2015-1982

[40]Luckring M,Hummel D 2013Aerosp.Sci.Technol.24 77

[41]Chu J,Luckring M 1996Experimental Surface Pressure Data Obtained on 65 deg Delta Wing Across Reynolds Number and Mach Number Ranges.Vol.3:Medium-Radius Leading Edge(Washington,DC:Ames Research Center,NASA)NASA-TM-4645-Vol-3

[42]Luckring M 2013Aerosp.Sci.Technol.24 10

High-order detached-eddy simulation method based on a Reynolds-stress background model∗

Wang Sheng-Ye1)Wang Guang-Xue2)Dong Yi-Dao1)Deng Xiao-Gang1)†

1)(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)
2)(School of Physics,Sun Yat-sen University,Guangzhou 510275,China)

20 March 2017;revised manuscript

14 May 2017)

Referring to the construction of shear stress transport-improved delayed detached-eddy simulation(SST-IDDES)method,a variant of IDDES method based on the Speziale-Sarkar-Gatski/Launder–Reece–Rodi(SSG/LRR)-ωReynoldsstress model(RSM)as Reynolds-averaged Navier-Stokes(RANS)background model,is proposed.Through combining high-order weighted compact nonlinear scheme(WCNS),the SSG/LRR-IDDES method is applied to three aeronautic cases and compared with traditional methods:SST-unsteady Reynolds-averaged Navier-Stokes(URANS),SSG/LRRURANS,and SST-IDDES.To verify the SSG/LRR-IDDES method in simulating airfoil stalled flow,NACA0012 airfoil is adopted separately at attack angles of 17◦,45◦and 60◦.At the attack angle of 17◦,SST-URANS,SSG/LRR-URANS,and SST-IDDES methods each predict a higher lift coefficient than the experimental data,while the SSG/LRR-IDDES method obtains a better lift coefficient result and a higher fidelity vortical flow structure.It indicates that the RSM can improve the prediction of RANS-mode for pressure-induced separations on airfoil surfaces in detached-eddy simulation.At the attack angles of 45◦and 60◦,the SSG/LRR-IDDES method captures the massively separated flow with threedimensional vortical structures and obtains a good result,which is the same as that from the traditional SST-IDDES method.To indicate the improvement of the SSG/LRR-IDDES method in simulating airfoil trailing edge separation,NACA4412 airfoil is adopted.At the attack angle of 12◦(maximum lift),the trailing edge separation is mainly induced by pressure gradient.The SSG/LRR-IDDES method can predict the separation process reasonably and obtains a good lift coefficient and location of separation compared with experimental results.However,none of other methods can predict trailing edge separation.It confirms that when RSM is adopted as RANS background model in detached-eddy simulation,the ability to predict pressure-induced separation on airfoil surface is improved.For further verifying the SSG/LRR-IDDES method for simulating three-dimensional separated flow,blunt-edge deltawing at the attack angle of 24.6◦is adopted.At this attack angle,the primary vortex will break,which is difficult to predict by using the SSTURANS method.For the SSG/LRR-URANS method,it predicts the vortex breakdown successfully,but the breakdown process does not show any significant unsteady characteristic.The SST-IDDES and the SSG/LRR-IDDES methods both predict a significant unsteady vortex breakdown.But in terms of the accuracy of surface pressure and the fidelity of unsteady flow,the result obtained by the SSG/LRR-IDDES method is better than by the SST-IDDES method.

turbulence flows,Reynolds stress model,detached eddy simulation,weighted compact nonlinear scheme

(2017年3月20日收到;2017年5月14日收到修改稿)

基于Speziale-Sarkar-Gatski/Launder-Reece-Rodi(SSG/LRR)-ω雷诺应力模型发展了一类分离涡模拟方法,结合高精度加权紧致非线性格式在典型翼型及三角翼算例中进行了验证,并和传统基于线性涡粘模型的分离涡模拟方法进行了对比.结果表明:基于SSG/LRR-ω模型的分离涡模拟方法,提高了原雷诺应力模型对非定常分离湍流的模拟能力;同时相比于传统基于线性涡粘模型的分离涡模拟方法,尤其是在翼型最大升力迎角和三角翼涡破裂迎角附近,该方法在平均气动力预测的准确度、分离湍流模拟的精细度等方面更加优秀.

10.7498/aps.66.184701

∗国防科学技术大学科研计划(批准号:ZDYYJCYJ20140101)资助的课题.

†通信作者.E-mail:xgdeng2000@vip.sina.com

感谢中山大学国家超级计算广州中心在计算资源方面提供的帮助.

PACS:47.27.–i,47.27.em,47.27.ep,47.11.BcDOI:10.7498/aps.66.184701

*Project supported by the Foundation of the National University of Defense Technology of China(Grant No.ZDYYJCYJ20140101).

†Corresponding author.E-mail:xgdeng2000@vip.sina.com