机场巴士线网可靠性优化模型及算法设计*
包丹文 刘建荣 顾佳羽
(1.南京航空航天大学 民航学院,江苏 南京 210016;2.华南理工大学 土木与交通学院, 广东 广州 510640)
机场巴士线网可靠性优化模型及算法设计*
包丹文1刘建荣2†顾佳羽1
(1.南京航空航天大学 民航学院,江苏 南京 210016;2.华南理工大学 土木与交通学院, 广东 广州 510640)
建立了基于BP神经网络的机场巴士行程时间可靠性预测模型,量化了机场巴士线网可靠性程度,并以可靠性最大化为目标,综合考虑时间、站点、服务等约束条件,构建了机场巴士线网优化模型.然后采用爬山算法获取线路初始解,以可靠性建立适应度函数,采用不同变异率、交叉率设计混合遗传算法进行求解.实例研究结果显示:高峰时段南京禄口机场巴士线网可靠性仅为0.62,城区内路段可靠性较城区外低约15%,整体可靠性水平偏低;采用混合遗传算法的优化过程受交叉率、变异率影响大,较低的交叉率和较大的变异率会增加寻优过程的不稳定性;采用交叉率0.9、变异率0.05的模型时目标函数值为0.79,可靠性水平较优化前提升了11.5%,优化效果显著.该方法为优化机场巴士线网、提升机场对外交通服务效率提供了科学依据.
机场巴士;行程时间可靠性;BP神经网络;遗传算法;线网优化
航空运输正逐步成为我国居民出行的重要交通方式之一,在机场轨道交通尚未普及的情况下,地面交通方式特别是机场巴士仍然是联系机场主要方式,机场巴士线路布局是否科学合理直接关系到旅客通达机场的便捷性,从而对航空运输服务质量和效率产生重要影响.目前关于机场巴士线网规划方面的研究取得了不少成果,美国联邦航空管理局于1998年提出了机场地面交通线网规划的5步骤[1],被大部分学者广泛使用.Lu等[2]基于5步骤规划方法,提出了加利福尼亚机场交通衔接的定性和定量相结合的规划方法;黎晴[3]对5步骤规划方法进行了拓展,从预测、评价、调查、方案制定及优化等角度提出了机场地面交通线网的规划框架;还有部分学者根据运输通道规划理论,采用滚动迭代法、节点重要度法或最大熵法,对机场巴士线路配置规模、建设时机等方面开展研究[4-7],但这类研究尚未涉及到线路布局优化等具体方法,在实践应用中操作性不强;近年来,随着交通信息化程度提升,越来越多的学者将地理信息系统、计算机仿真手段应用到机场巴士线网优化方法研究中,例如陆婧[8]以成本最小为目标,构建了机场巴士线路及运营优化模型;周和平等[9]以旅客出行时间最小构建了机场巴士线网优化模型,并利用混合遗传算法求解;Abdelaziz等[10]将机场巴士路径问题视为随机车辆路径问题,并以成本最低、满足所有客户时间需求、旅客旅行时间最低以及机场等待时间最低构建了多目标线网优化模型,最后以突尼斯-迦太基国际机场真实数据对该模型进行了测试;文献[11-13]中制定了机场巴士、常规公交等方式在线路走向、班次安排以及运营时间方面的组织方法,研究成果为科学规划与设计机场巴士提供了理论支撑,但研究中缺乏对旅客出行可靠性方面的考虑.通达机场的可靠性已经成为机场旅客满意度评价中最为关注的因素,而机场巴士线路极易受到地面交通拥堵、突发性事故等多种不确定性因素的影响,这类随机性因素直接影响到旅客出行过程中的可靠性.据不完全统计,首都机场高速发生交通拥堵的概率约为8.4%,由此造成旅客误机的比例高达10%.关于出行可靠性测算方法的研究可归纳为两类:模拟法和解析法.模拟法假定路段容量及交通需求服从某一特定的分布,利用确定型或随机型用户均衡模型反复执行交通流分配,在获得海量样本数据的基础上,利用Monte Carlo抽样等方法对出行时间可靠性分析评价[14-16].解析法则假定出行时间服从某种概率分布,然后通过概率论与数理统计中的解析方法计算出行时间的均值和标准差,进而获得出行时间可靠度指标[17-19].
虽然上述研究已在机场巴士线网优化方面取得了一定的成果,但仍存在一些不足,主要体现在以下三方面:① 机场巴士线网的优化多以旅客出行时间、线路运营成本或线网密度等指标为目标,较少考虑旅客对于出行可靠性的需求;② 少数学者将可靠性理论应用到巴士线网的优化中,但多采用连通可靠性指标对不同优化方案的可靠性进行评价,对于行程时间可靠性的研究较少;③ 传统行程时间可靠性测算方法多适用于供需条件相对稳定的环境,当交通条件受外部环境影响变化较大时,例如道路拓宽、流量变化或路线调整时,既有方法难以准确量化机场巴士线网可靠性的变化.
有鉴于此,文中在既有研究基础上对机场巴士线网优化问题进行深入研究,将旅客行程时间可靠性引入到机场巴士线网优化过程中,通过建立基于BP神经网络的行程时间可靠性预测方法,量化机场巴士线网可靠性程度,并构建基于可靠性的机场巴士线网优化模型,同时设计求解算法,为科学优化机场巴士线网、提高运行可靠性、提升机场对外交通服务效率提供理论方法.
1 机场巴士线网可靠性概念
结合行程时间可靠性的定义,将机场巴士线网可靠性定义为在规定时间阈值内机场巴士到达目的地的概率.假设一条机场巴士线路如图1所示.
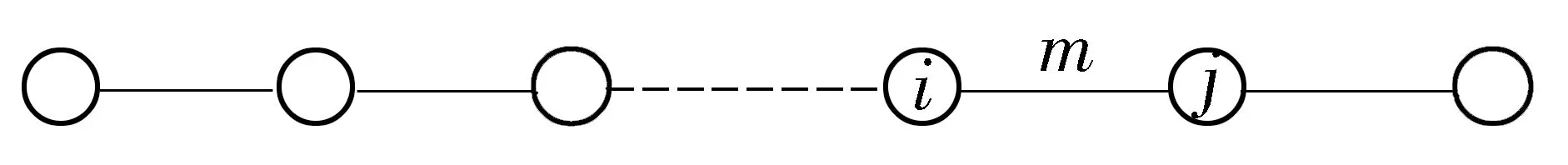
图1 机场巴士线路示意图
Fig.1 Schematic diagram of airport bus line
图中i、j为站点,m为路段,则站点i、j之间路段m的行程时间可靠性计算公式如下:
Rijm=P(tijm≤Tijm)
(1)
其中:
tijm=tm+ti+tj
(2)
Tijm=Tm+Ti+Tj
(3)
(4)
Ti=To+Tc+Tpi
(5)
Tpi=quiTu+qdiTd
(6)
式中:Rijm为机场巴士站点i、j之间路段m的行程时间可靠性;tijm为路段m的行程时间,由路段m的行驶时间tm和i、j站点上下客时间ti、tj组成;Tijm为路段m的行程时间阈值,由路段m的行驶时间阈值Tm和站点上下客时间阈值Ti、Tj组成;Lm为路段m的长度;Vm为路段m的可接受的机场巴士行驶速度(高速公路取80 km/h,主干道取40 km/h);To、Tc分别为巴士开、关门时间(取3 s);Tpi为站点i旅客上、下车时间;qui、qdi分别为站点i上、下车旅客数;Tu、Td分别为可接受的人均上、下车时间(取2.5 s).
机场巴士线路是由多条路段串联而成,因此机场巴士线路可靠性由相互串联的路段可靠性所决定,计算公式如下:
(7)
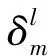
目前关于机场巴士线网行程时间可靠性的计算方法通常有3种:取各条线路可靠性的最小值、数学平均值或加权平均值,第3种方法的结果相对准确.因此文中将机场巴士线网行程时间可靠性定义为所有机场巴士线路行程时间可靠性的加权平均值,每条线路的权重为该线路客流量占线网客流量的比例,计算式如下:
(8)
式中,Rnet为机场巴士线网的行程时间可靠性,Rl为机场巴士线路l的行程时间可靠性,ql为机场巴士线路l的客流量,M为线网中机场巴士线路数.
2 模型构建
2.1 机场巴士可靠性预测模型
BP神经网络能够基于样本数据,通过自动调整网络的连接权值实现输入变量到输出变量的任意非线性联系该方法对样本数量要求相对不大,并且具有自我学习及组织能力,自适应性强,容错性强,在数据识别、预测、分类等领域应用广泛.因此文中采用Matlab工具,构建基于BP神经网络的机场巴士行程时间可靠性测算模型,主要步骤如下.
步骤1 变量选择与预处理
输出变量:通过交通调查,获取机场巴士各路段多组实际行程时间数据,利用式(1)计算得到各路段行程时间可靠性,并作为输出变量.
输入变量:影响机场巴士可靠性的主要因素有两类,即交通设施特征和交通流状态,因此初步选取道路等级、车道数、路段长度、交叉口数量、流量、行程时间、行驶速度、小汽车比例、饱和度作为输入变量[20].运用SPSS软件对输入、输出变量相关性进行分析,确定机场巴士行程时间可靠性的影响因素.
归一化处理:为了消除数据不同量纲对预测结果影响,对各变量进行归一化处理,计算公式如下:
Y=(X-Xmin)/(Xmax-Xmin)
(9)
X=Xmin+Y(Xmax-Xmin)
(10)
式中,Y为归一化后的数据,X为原始数据,Xmin为数据最小值,Xmax为数据最大值.
步骤2 隐层节点数选择
步骤3 网络训练与测试
分别采用traingdx、traingdm、traingd、trainlm 4种函数进行训练,选取最佳训练函数,并得到最终训练结果.
2.2 机场巴士线网优化模型
可靠性水平是旅客通达机场过程中最为关注的指标之一,也是提高机场巴士服务水平的主要因素,因此文中以高峰时段机场巴士线网行程时间可靠性水平最高为目标,建立机场巴士线网优化模型,目标函数如下:
(11)
式中,Fmax为目标函数,Rnet为机场巴士线网可靠性,αijm为权重系数,Rijm为站点i、j之间路段m的行程时间可靠性,qijm为路段m的旅客量,Xijm、Yim为决策变量.
约束条件:
(12)
(13)
(14)
M≤6
(15)
(16)
式中:时间约束tijm为机场巴士线路m在站点i到j间的行驶时间,T为线路最大运行时间;站点约束Amin、Amax分别为单条线路最小以及最大停靠站点数;服务约束d为一个站点最多能经过的线路数;线路约束M为机场巴士线路数量;盈利约束qm为线路m的旅客量,C为机场巴士票价;S为机场巴士单位里程运营成本.
3 算法设计
上述模型采用混合遗传算法求解[9],其基本思路是将爬山算法和遗传算法相结合,利用爬山算法局部搜索能力强的优点,首先确定初始线路,避免搜索过程陷入局部最优解;然后开始全局最优解搜索过程,确定遗传算法的编码形式,通过选择、交叉、变异操作产生新的个体,反复迭代直到满足终止条件.具体计算步骤如下:
第1步个体编码.采用数字对机场巴士站点进行直接编码.若站点总数8个,2条线路,则机场编为1,首末站分别编为2、3,中途站点编为4-9,线路编码为2-4-7-9-1、3-4-5-6-8-1;
第2步初始群体产生.随机选择n个始发站点,采用爬山搜索法确定n条初始路线,组合多条线路编码为一个串,产生N个染色体组成初始种群,具体计算步骤如下:
步骤1 随机产生n个互不重复的自然数xi(i=1,2,…,n),令f=f(xi),k=1;
步骤2P为xi的领域,设xi为当前最优解,则xbest=xi,即p=M(xbest);
步骤3 从p中任选一个解yi,若f(yi)>f(xi),则令f=f(yi)、xi=yi,转步骤2,否则转步骤4;
步骤4 令k=k+1,若k<2n,转步骤2,否则转步骤5;
步骤5 终止算法,输出最优解.
其中f(x)采用上文可靠性预测方法计算.
第3步适应度评估方法确定.依次计算上述初始线网的约束条件,若有一项不符合则剔除;剩余染色体目标函数值Zi(i=1,2,…,N),则个体适应度p=zi/∑zi.
第4步选择操作.采用最佳个体保留与赌轮选择相结合的策略,将群体中个体按适应度从大到小排列,排在第一位的个体直接保存到下一代,保证最优个体不会被遗传操作破坏;其余N-1个个体根据适应度,采用轮盘选择产生.
第5步交叉操作.对选择操作产生的新群体,按交叉概率Pc进行配对交叉,随机选择一个断点,采用双亲遗传法,交换双亲上断点的右端,生成新的后代.
第6步变异操作.从种群中随机选取一个个体,对选中的个体以变异概率Pm改变某个基因.
第7步终止原则.种群中使得目标函数达到最小的个体作为最终计算结果输出.
4 实例应用
4.1 数据获取及分析
本次研究以南京市禄口机场为例,通过交通调查获取以下两类数据.
(1)机场巴士线路属性特征
目前禄口机场共开设机场巴士线路6条,线路分布如图2所示.通过机场航站楼管理部获取每条机场巴士线路、站点属性特征,如表1所示.
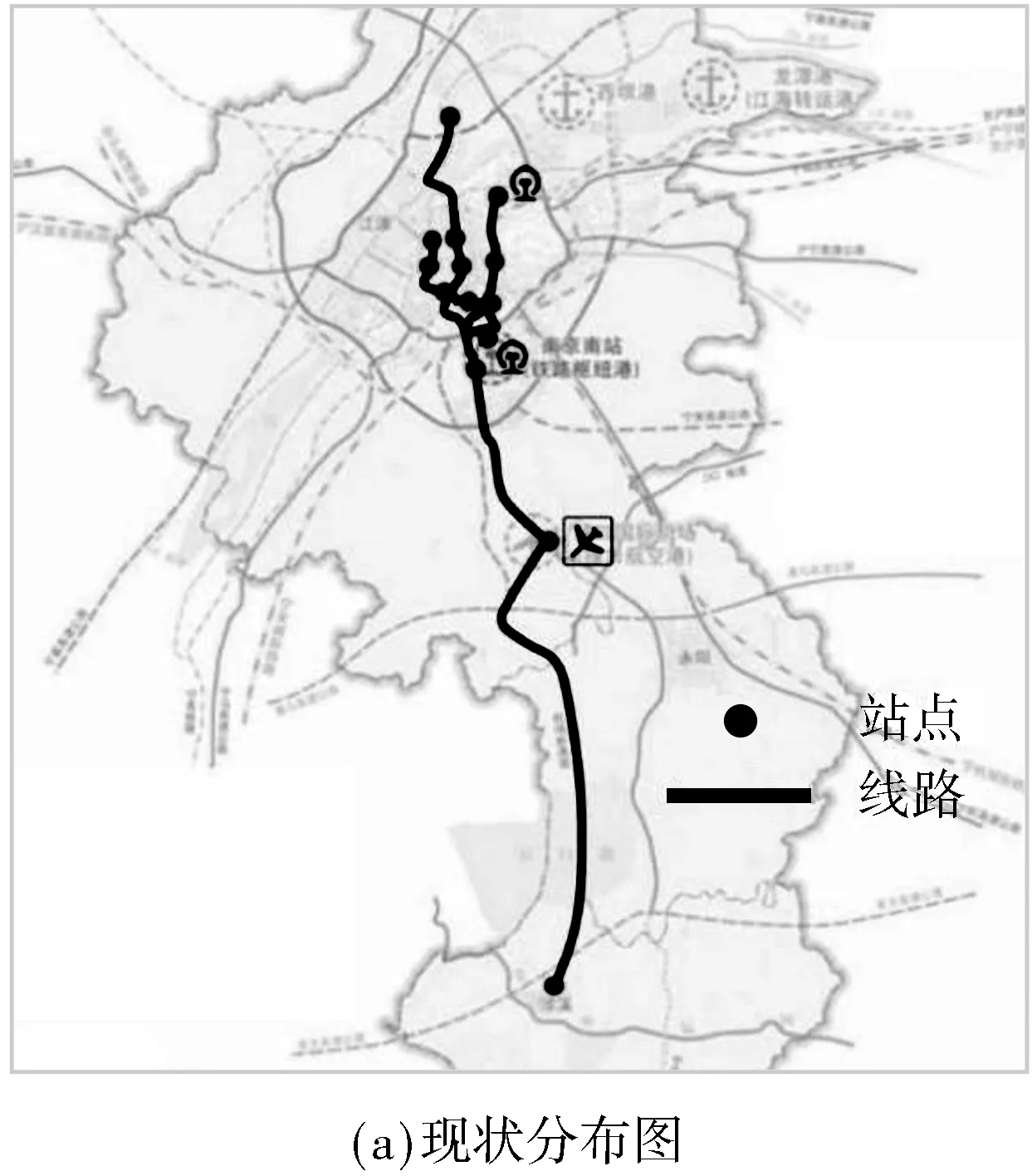
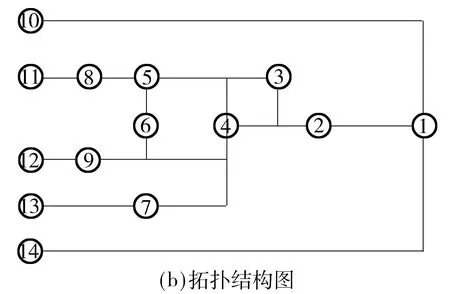
图2 禄口机场巴士线路现状分布以及拓扑结构图Fig.2 Status quo of Lukou airport bus line distribution and topological structure diagram
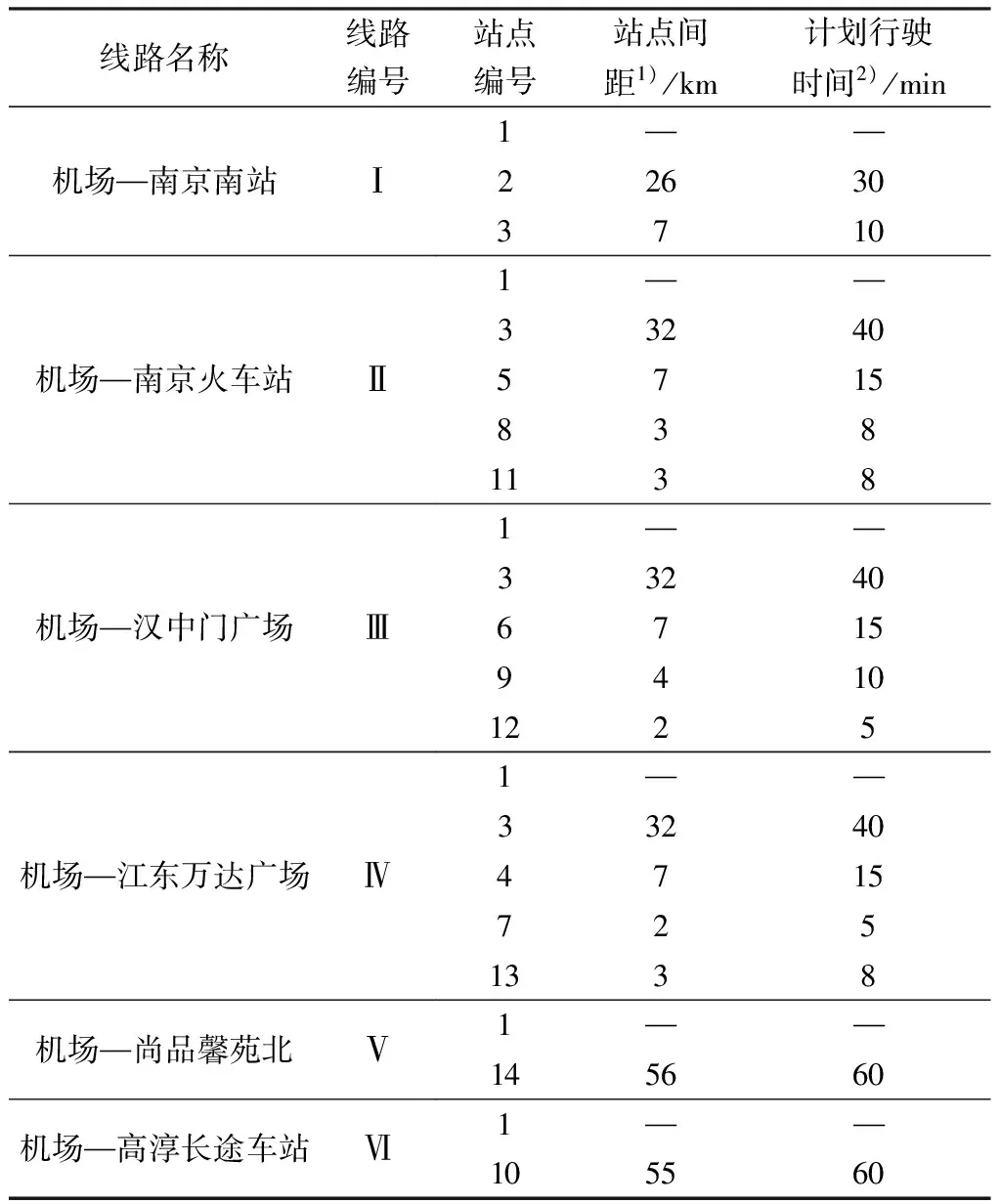
表1 机场巴士线路基本属性汇总表Table 1 Summary of basic attributes of airport bus line
1)站点间距为本站点与上一站点之间行驶距离;2)计划行驶时间为机场巴士在本站点与上一站点之间的计划通过时间,即路段行程时间阈值.
(2)机场巴士线路运行特征
本次交通调查通过开展上下客调查、运行延误调查、运行环境调查3项调查工作,获取路段长度、路段流量、路段行驶时间、路段行驶速度、路段旅客数、站点上下旅客数、站点停靠时间等指标数据,具体调查方案如下:
①上下客调查采用随车调查法,每辆机场巴士上安排1名调查员,跟车记录每个站点上下客人数、路段旅客数.
②运行延误调查采用GPS跟车计时调查法,利用行车仪记录下机场巴士运营全过程,获取各路段行驶时间、路段行驶速度、站点停靠时间.
③运行环境调查采用现场调查法,每个路段安排1名调查员,记录路段等级、车道数、交叉口数量、流量、小汽车比例.
调查时间为2015年12月9日(周二),高峰7:00~8:00以及平峰14:00~15:00,获取6条机场巴士线路14个站点平均上下客人数,以及各条路段平均旅客数;同时安排调查员20名、行车仪8部、路段观测点15个,获取机场巴士路段运行特征数据22组,调查结果如表2所示.
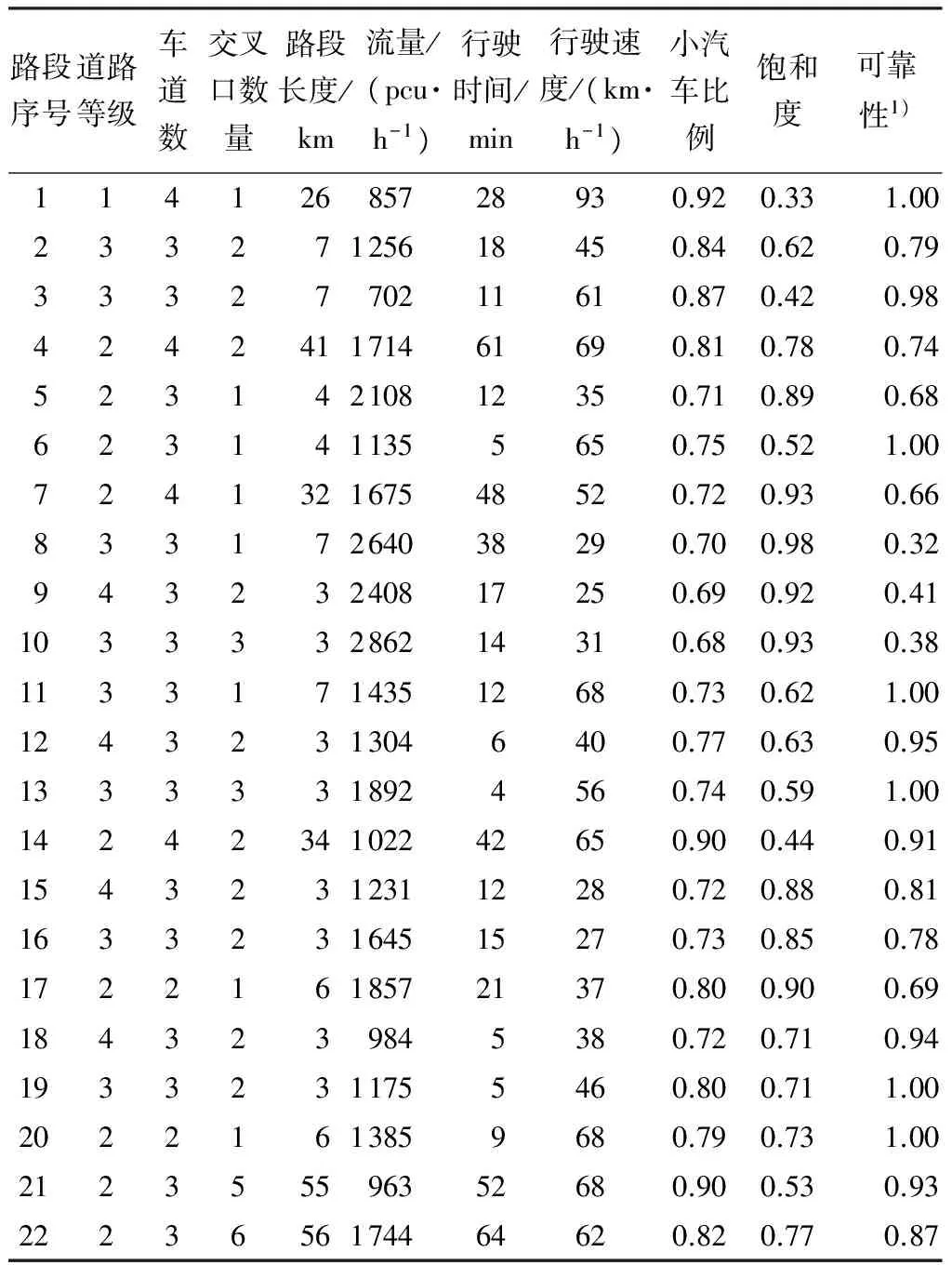
表2 机场巴士运行特征数据汇总表Table 2 Summary of the statistics of airport bus operating characteristics
1)将调查数据代入式(1)可计算得到可靠性.
4.2 可靠性预测结果
根据2.1节中可靠性预测模型,首先确定输入及输出变量,其中输出变量各路段可靠性值见表2.运用SPSS分析变量之间的相关性,认为相关系数在0.8以上的因素之间有较强的相关性,由此选择道路等级、路段长度、流量、行驶速度、小汽车比例和饱和度为最终输入变量.
计算隐层节点数,制定测试方案分别为6、8、10、12、14个隐层节点,对22组数据进行测试,训练结果显示,当隐层节点数为10个时,样本绝对均方差最小,从而确定隐层节点数为10,如图3所示.
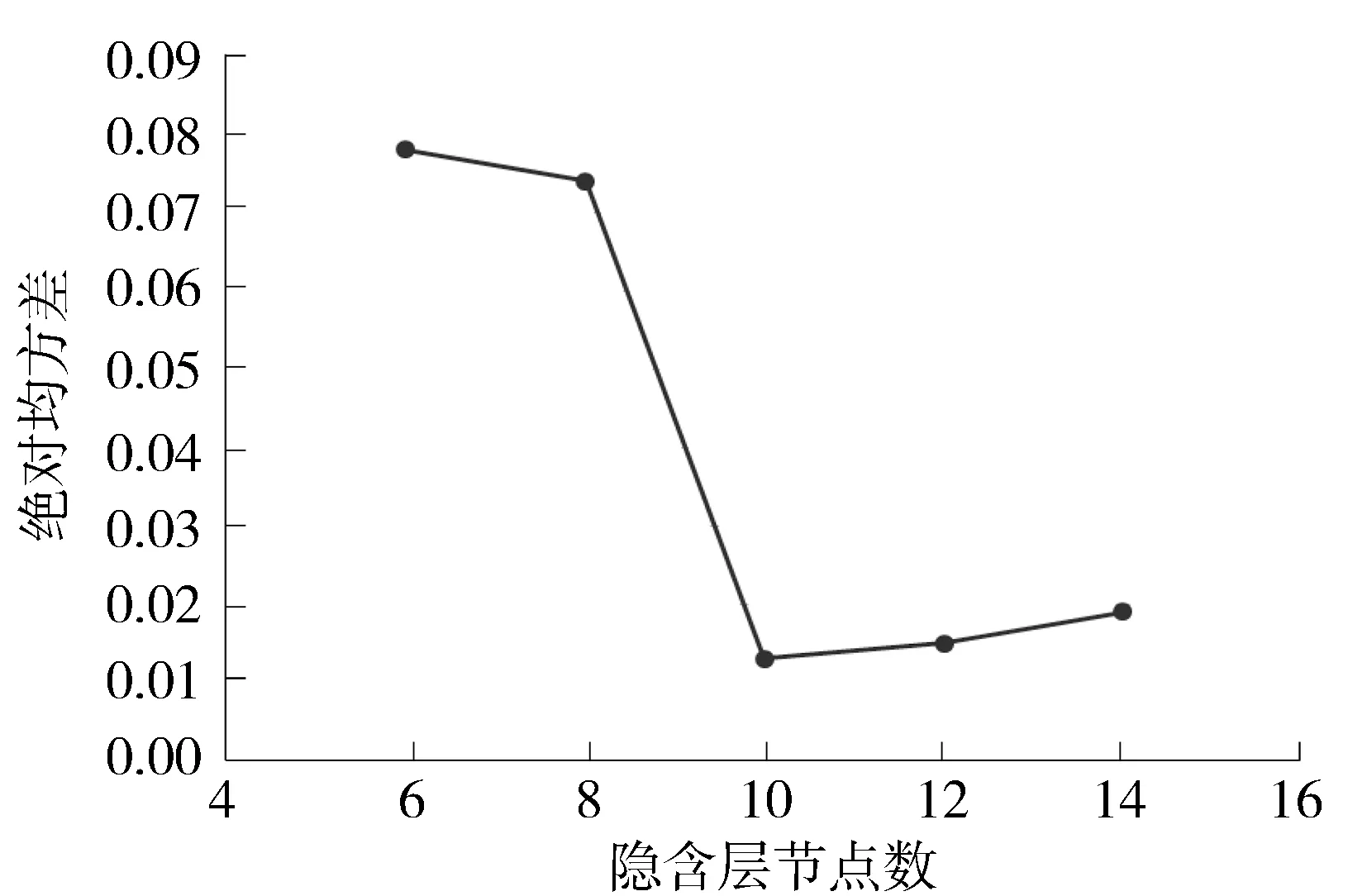
图3 不同隐层节点数的绝对方差值Fig.3 Absolute variance value of the numbers of different hidden layer nodes
分别采用Traingdx,Traingdm,Traingd,Trainlm 4种训练函数,网络训练图如图4所示.误差分析结果如表3所示.
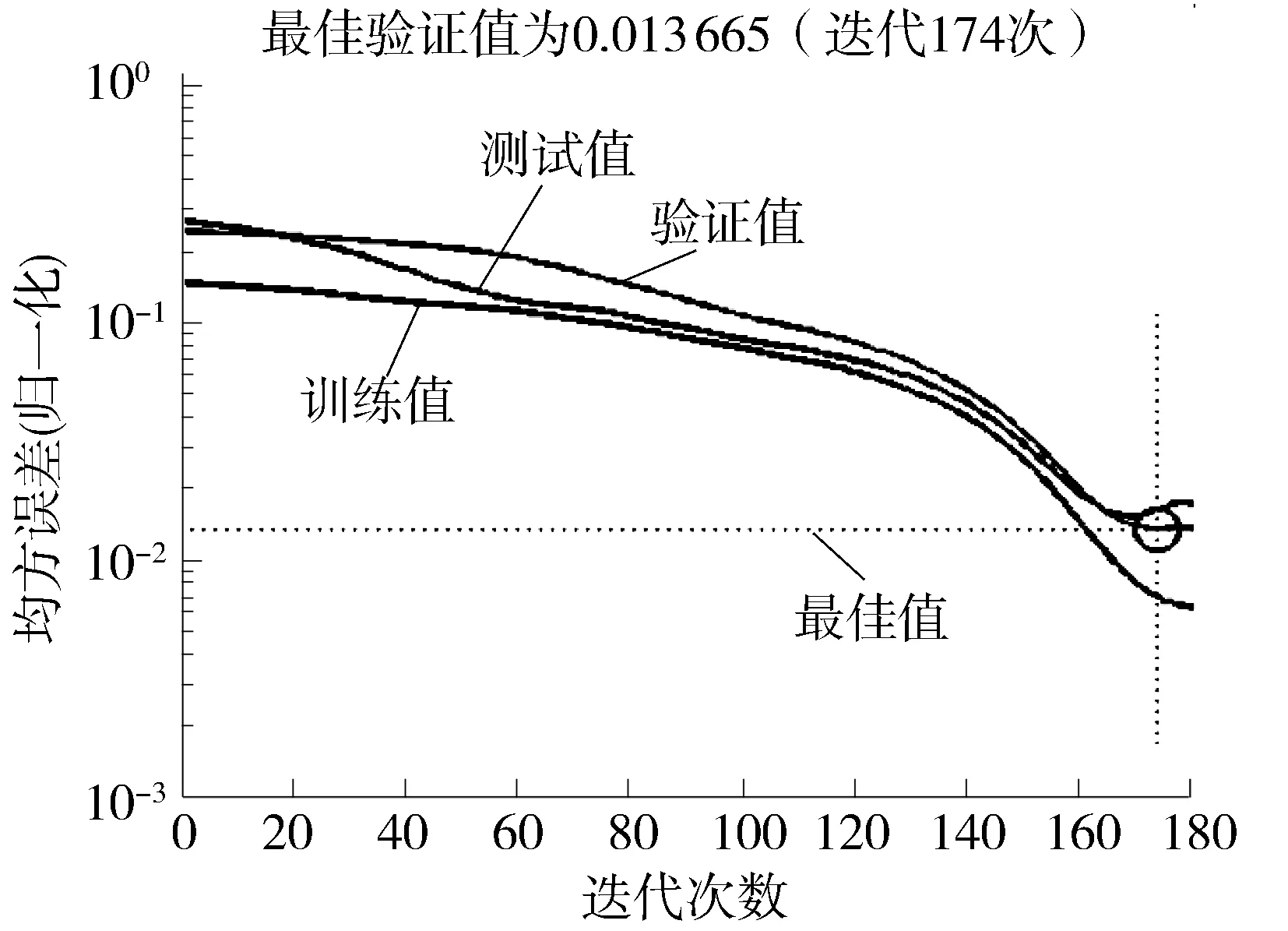
图4 网络训练图Fig.4 Network training diagram
结果显示,traingdx函数的预测精度相对较高,网络在第174次训练得到最佳验证集绝对误差0.06.同时文中对预测值和调查值进行回归拟合,分析结果如图5所示,检验结果r2为0.876 6,模型具有较高精度,该模型可以用于机场巴士线网可靠性的测算.然后将机场巴士各路段单元的输入变量输入该模型中,便可获得基于BP神经网络的机场巴士各路段行程时间可靠性测算结果如图6所示,其计算结果如表4所示.根据式(7)和(8),计算得到高峰时段机场巴士线网可靠性为0.57;平峰时段可靠性为0.88.结果显示,高峰时段机场巴士各路段行程时间可靠性仅约0.6,40%旅客无法在时间阈值范围内到达机场,可靠性比平峰时段低26.4%,;机场巴士线路在城区内运行可靠性明显低于城区外围,城区内80%路段行程时间可靠性低于0.68,较城区外低约25%;相同路段不同方向的可靠性也有所不同,受高峰时段进程车辆影响,城区内下行路线可靠性明显偏低,较上行路线低10%,可见高峰时段机场巴士可靠性受道路运行条件影响大,应合理优化机场巴士路线,提高旅客通达机场可靠性.
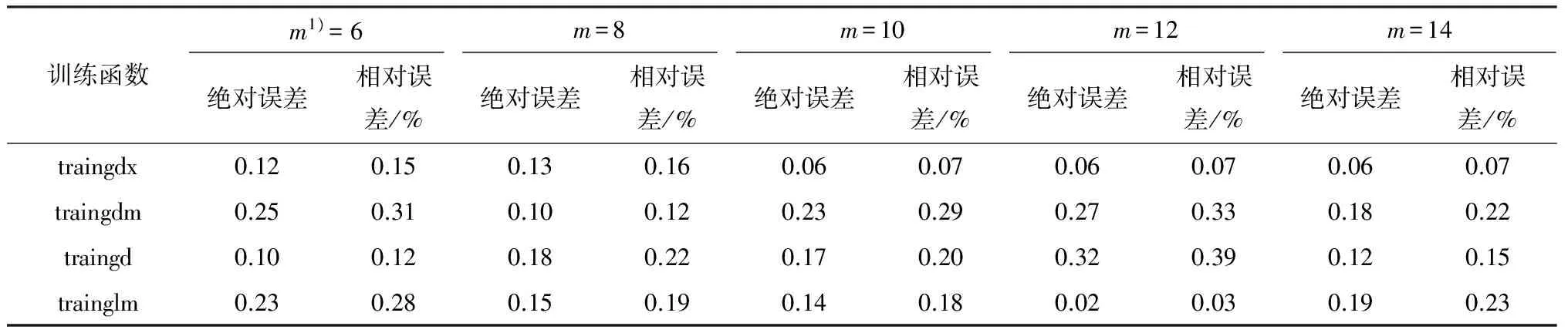
表3 不同训练函数结果误差分析表Table 3 Error analysis of different training function results
1)m为隐含层节点数.
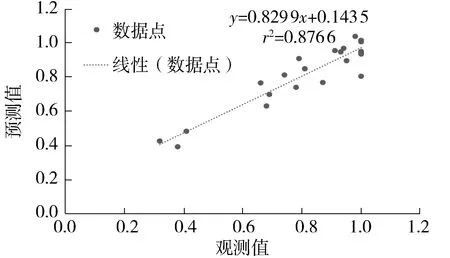
图5 预测值与观测值回归分析图Fig.5 Regression analysis of predicted and observed values
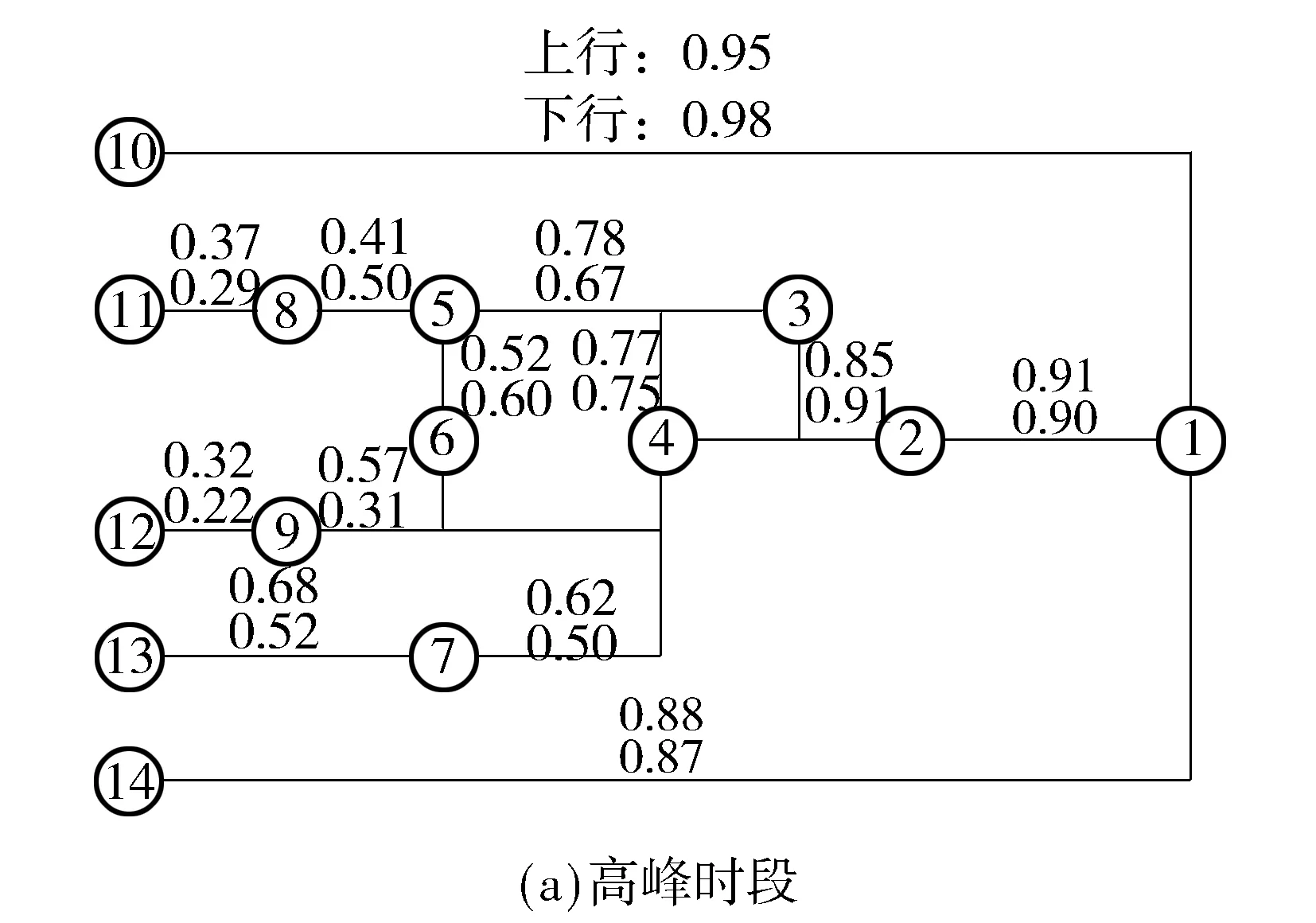
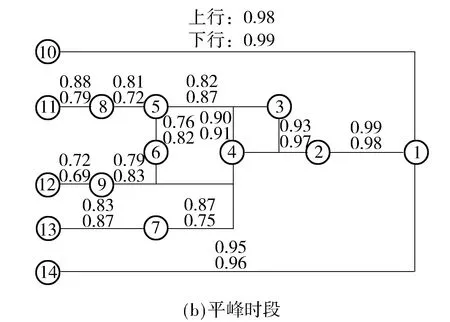
图6 南京禄口机场巴士线网各路段可靠性分布图Fig.6 Reliability distribution of each section of Nanjing Lukou airport's bus line network
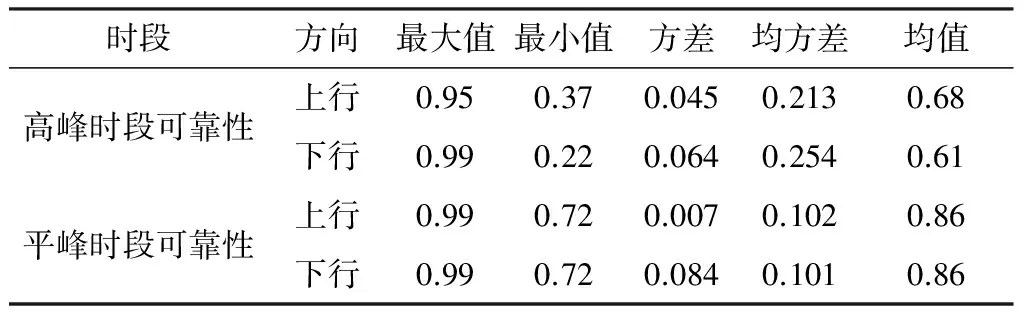
表4 机场巴士线网各路段可靠性计算结果Table 4 Results of reliability calculation of airport bus line sections
4.3 线网优化方案
根据南京禄口机场巴士站点及道路分布现状,对既有巴士线网进行调整完善,构建用于测试的机场巴士线网如图7所示,站点14个,路段18条,各路段等级、长度、高峰小时流量、行驶速度、车流比例、饱和度等特征数据见表1、4,未调查路段参数取同等级别道路平均值.本次优化共设置机场巴士线路6条,每条线路站点数2-6个(含机场站),线路最长运行时间90 min;单个站点最多服务线路数3条;机场巴士盈利率25%,票价25元/人,运营成本8元/km,则有:M=(1,2,3,4,5,6),N=(1,2,3,…,14),T=90 min,Amin=2,Amax=6,ε=25%,d=3,S=8,C=25.
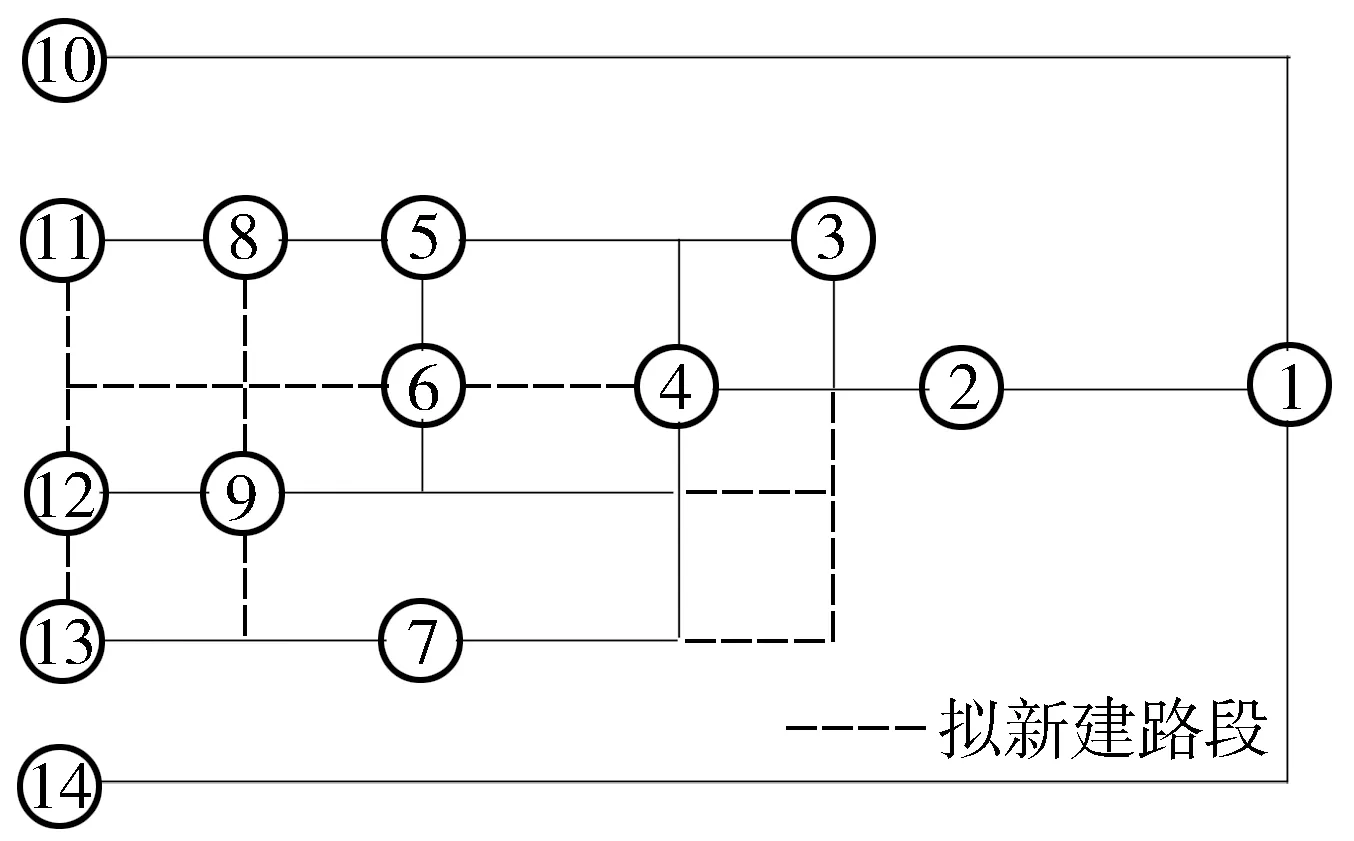
图7 优化后的机场巴士路网拓扑结构Fig.7 Topological structure of airport bus network after optimization
利用Matlab软件,基于上文提出的算法步骤进行仿真运算,取不同变异率和交叉率进行迭代,结果表明:较低的交叉率和较大的变异率会增加寻优的不稳定性,最终确定采用交叉率0.9、变异率0.05,得到测试结果如图8所示,线网优化结果如表5所示.模型目标函数值为0.79,即优化后高峰小时机场巴士线网可靠性为0.79,较优化前的0.57提升了38.5%.
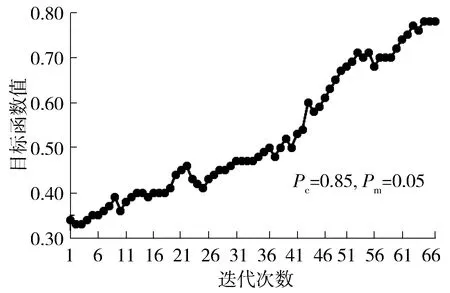
图8 算法测试结果图Fig.8 Test results of the algorithm
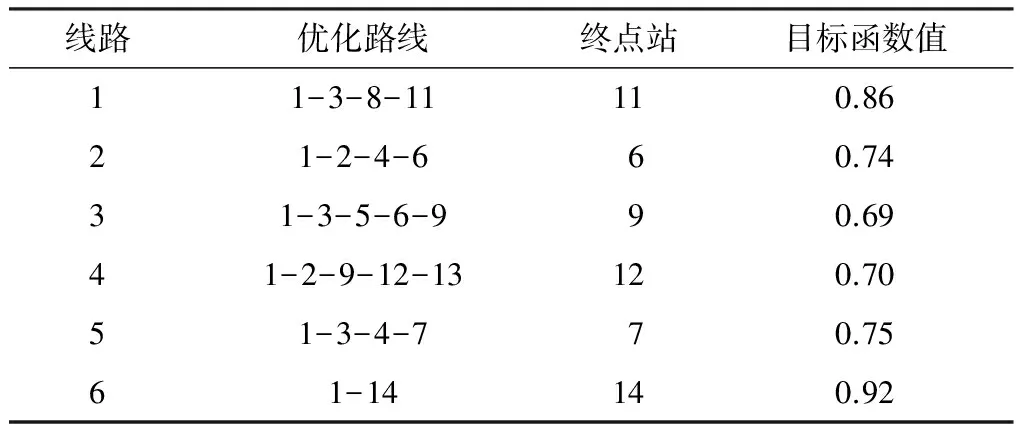
表5 线路优化结果表Table 5 Results of airport bus line optimization
5 结语
首先,文中在分析行程时间可靠性影响因素基础上,构建了基于BP神经网络的机场巴士行程时间可靠性预测模型,并通过南京禄口机场实例对模型进行了检验,证明模型具有较高精度.研究显示:高峰时段机场巴士可靠性受交通运行状况影响显著,机场巴士线网可靠性仅为0.62,40%旅客无法在时间阈值范围内到达机场;城区内路段行程时间可靠性均低于0.68,可靠性水平较外围路段低约25%,该方法为优化机场巴士线网提供了理论依据.
其次,文中以机场巴士线网可靠性最大为目标,综合考虑时间、站点、服务等约束条件,构建了机场巴士线网优化模型,并以爬山算法获取线路初始解,以可靠性建立适应度函数,采用不同变异率、交叉率设计混合遗传算法求解.实例测算结果表明,较低的交叉率和较大的变异率会增加寻优过程的不稳定性,采用交叉率0.9、变异率0.05的模型,目标函数值为0.79,可靠性水平较优化前提升了11.5%,优化效果显著.
文中提出的方法可用于机场巴士线网优化,具有一定的理论意义.同时该方法为提高机场巴士运行可靠性、提升机场对外交通服务效率提供了一种途径,具有较高的实践价值.未来还需要对机场巴士线网优化模型算法进行深入探讨,重点对线路初始种群确定、寻优过程开展研究,进一步提高模型结果的准确性.
[1] The Federal Aviation Administration.ACRP report 4:Ground access to major airports by public transportation [R].Los Angeles:The New England Transportation Institute,2008.
[2] LU Xiao-yun,GOSLIN G D,XIONG Jing.Opportunities for improved intermodal connectivity at California airports [R].Berkeley:University of California,1995.
[3] 黎晴.机场陆侧交通问题研究 [D].上海:同济大学,2004.
[4] 李德刚.综合运输网中的通道分析与系统配置研究 [D].成都:西南交通大学,2006.
[5] 杨庆云,翟永红.浅析机场巴士客运 [J].黑龙江交通科技,2009(6):210-213.
YANG Qing-yun,ZHAI Yong-hong.The analysis of airport bus passenger transport [J].Communications Science and Technology Heilongjiang,2009(6):210-213.
[6] 潘虹.基于机场轨道交通的机场巴士线路优化调整研究 [J].交通与运输(学术版),2011(2):106-110.
PAN Hong.Research of airport bus route optimal adjustment based on airport rail transit [J].Traffic & Transportation,2011(2):106-110.
[7] LACOMBER A.Ground access to airports:prospects from intermodalism [J].Transportation Quarterly,2004,48(4):381-392.
[8] 陆蜻.轴辐式机场长途巴士线网的运营时刻表优化 [D].大连:大连海事大学,2011.
[9] 周和平,贾赞星,柳伍生.基于混合遗传算法的机场巴士线路优化 [J].长沙理工大学学报(自然科学版),2012,9(4):12-17.
ZHOU He-ping,JIA Zan-xing,LIU Wu-sheng.The optimization method to airport bus routes based on hybrid gene-tic algorithm [J].Journal of Changsha University of Science and Technology(Natural Science),2012,9(4):12-17.
[10] ABDELAZIZ F B,MASRI H,ALAYA H.A recourse goal programming approach for airport bus routing problem [J].Annals of Operations Research,2015,251(1):1-14.
[11] KIVETT H.Lessons for rail access to airports [J].International Air Transportation Conference,2001,12(5):96-105.
[12] TAMBI J,GRIEBENOW B.Automated guide way transit to provide access to New York city airports [J].4th International Conference on Automated People Movers,2003,8(4):121-130.
[13] LU J,YANG Z,TIMMERMANS H,et al.Optimization of airport bus timetable in cultivation period considering passenger dynamic airport choice under conditions of uncertainty [J].Transportation Research Part C Emerging Technologies,2016(67):15-30.
[14] 刘勇,项莉,谢军,等.城市路网可靠性计算方法 [J].交通运输工程学报,2007,3(7):95-99.
LIU Yong,XIANG Li,XIE Jun,et al.Reliability computation method of urban road network [J].Journal of Traffic and Transportation Engineering,2007,3(7):95-99.
[15] 陈玲娟,蒲云.基于粒子群算法的双目标可靠性网络设计 [J].交通运输工程学报,2010,5(10):61-65.
CHEN Ling-juan,PU Yun.Dual-objective reliable network design based on particle swarm optimization [J].Journal of Traffic and Transportation Engineering,2010,5(10):61-65.
[16] 陆婧.基于乘客选择习惯变化的机场长途巴士时刻表动态优化研究 [D].大连:大连海事大学,2015.
[17] 侯立文,蒋馥.城市道路网的可靠性仿真 [J].系统仿真学报,2008,14(5):664-668.
HOU Li-wen,JIANG Fu.The reliability simulation of urban road network [J].Journal of System Simulation,2008,14(5):664-668.
[18] 李小静.基于行程时间可靠性的城市交通网络分析 [D].兰州:兰州交通大学,2015.
[19] DIEPEN G,PIETERS B F,VAN D A,et al.Robust planning of airport platform buses [J].Computers & Operations Research,2013,40(3):747-757.
[20] 刘汶菠.基于行程时间可靠性的公交专用道线网优化决策研究 [D].成都:西南交通大学.2009.
s:Supported by the National Natural Science Foundation of China(51508247)and the Natural Science Foundation of Jiangsu Province(BK20140821)
OptimizationModelofAirportBusLineNetworkReliabilityandAlgorithmDesign
BAODan-wen1LIUJian-rong2GUJia-yu1
(1. Collage of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, Jiangsu, China;2. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China)
In order to quantify the reliability of airport bus line networks, a reliability prediction model of the airport bus travel time is constructed based on the BP neural network. Next, an optimization model of the airport bus line network is constructed, the objective of which is to maximize the reliability, and such constraints as time, sites and services are taken into account. Then, the Hill-climbing algorithm is adopted to achieve the initial solutions for the lines, and a fitness function based on the reliability is established. Finally, a hybrid genetic algorithm with different mutation and crossover rates is designed to solve the constructed optimization model. Case study results show that (1) during peak hours, the reliability of the bus line network at Nanjing Lukou International Airport is only 0.62, the reliability of inner city roads is about 15% lower than that of outer city roads, and the overall reliability is at a low level; (2) the optimization process through the hybrid genetic algorithm is greatly affected by the crossover and mutation rates, and lower crossover rate and higher mutation rate can increase the instability of the optimization process; and (3) when the crossover rate is 0.9 and the mutation rate is 0.05, the objective function value of the constructed optimization model is 0.79, and the reliability is 11.5% higher than that before the optimization, which means that the optimization effect is significant. This method provides a scientific basis for the optimization of the bus line network of airports and the corresponding efficiency improvement of the external transport services.
airport bus; travel time reliability; BP neural network; genetic algorithm; line network optimization
2016-08-29
国家自然科学基金资助项目(51508247);江苏省自然科学基金资助项目(BK20140821)
包丹文(1982-),男,博士,讲师,主要从事交通运输规划与管理研究.E-mail:baodanwen@nuaa.edu.cn
†通信作者:刘建荣(1985-),男,博士,讲师,主要从事公共交通规划与设计研究.E-mail:ctjrliu@scut.edu.cn
1000-565X(2017)08-0084-08
U 491.2
10.3969/j.issn.1000-565X.2017.08.013

