转向架参数测定试验台位姿正解*

王启明 苏建 牛治慧 林慧英 徐观

(吉林大学 交通学院，吉林 长春 130025)

转向架参数测定试验台位姿正解*

王启明 苏建 牛治慧 林慧英†徐观

(吉林大学 交通学院，吉林 长春 130025)

并联机构位姿正解求解运用的Newton-Raphson迭代法对初值有很强依赖性，且收敛速度较慢，无法满足实时性要求.为此文中提出基于Levenberg-Marquardt(L-M)算法的改进BP分类神经网络结构模型和高阶收敛改进Newton-Raphson迭代法(HMNR)相结合求解并联机构位姿正解.以转向架参数测定试验台为例，借助位姿反解将轨道谱路谱转化成试验台作动器的伸缩量指令，将其给定到液压系统中，驱动试验台耦合运动模拟车体或转向架在该路谱线路上的运行状态.运用大量实际运行样本数据作为训练数据，实现了试验台位姿正解的初值求解，并与常用的基于拟牛顿算法(BFGS)的神经网络模型和量化共轭梯度(SCG)算法的神经网络模型进行对比分析.结果表明，L-M算法模型在误差性能分析上明显优于BFGS与SCG算法模型，且预测角度值误差均小于4×10-7,位移值误差均小于8×10-4. 将预测值作为HMNR法的初值，进行迭代计算，较之Newton-Raphson(NR)法迭代次数减少41%，迭代时间缩短23%.将此混合策略用于试验台，进行实际相邻车端相对位姿测量试验，进一步验证了该策略的有效性.

轨道车辆；位姿正解；冗余；6-DOF并联机构；Levenberg-Marquardt算法；高阶收敛

随着国民经济的高速发展，铁路车辆的速度不断提高，铁路运输压力也逐渐增大，客运高速和货运重载成为我国铁路发展的主要方向，但随之列车在高速行驶下的稳定性、可靠性及舒适性等成为了我国高速铁路发展中亟需解决的问题.车辆端部和转向架作为轨道车辆的重要组成部分，在车辆通过曲线轨道时各部件的状态对于车辆运行安全性及稳定性等动力学性能具有直接的影响.吉林大学汽车运输工程研究所研制的转向架参数测定试验台[1]能够在转向架总成状态和整车状态下对转向架的轨道运行工况动态模拟，并对转向架的动力学参数和结构力学参数动态测试.转向架参数测定试验台为六自由度并联机构，该并联机构位姿正解的求解精度和实时性对实现该机构的姿态大闭环控制、精度分析、位姿实时监测等有重大意义.目前，国内外对并联机构位姿正解的求解方法主要包括解析法、数值法和附加传感器法等.解析法[2]的不足之处在于求解难度大，编程不易实现，且求解的结构没有通用性等.传统数值法主要使用Newton-Raphson[3]法来求解其正解，该算法对初值较为敏感，不合适的初值将影响算法收敛速度甚至发散.而神经网络方法虽不需要考虑初值，且能够满足实时性的要求，但神经网络预测值稳定精准与否依赖于训练样本.因此，文中提出基于L-M算法的改进分类神经网络模型[4]，结合高阶收敛改进Newton-Raphson迭代法(HMNR)求解并联机构位姿正解.借助神经网络模型强大的非线性映射逼近能力，将试验台模拟轨道车辆在实际轨道上的运行姿态作为训练样本，通过大量样本学习预测出试验台的实时位姿量，将此值作为HMNR算法的初值进行最终迭代计算.既避免了迭代法选取初值的盲目性，又加快了计算速度，提高了位姿正解的求解精度.

1 转向架参数测定试验台

转向架参数测定试验台由前6-DOF运动平台子系统和后6-DOF运动平台子系统组成，是一种双6-DOF平台的并联机构.为了便于分析和模型构建，定义列车的前进方向为X轴，根据右手定则确定Y轴方向，铅直方向为Z轴.试验台内每个6-DOF运动子系统均由7套伺服液压作动器、14套消隙球铰、运动平台及支座构成.每套电液伺服作动器的两端都是通过消隙球铰连接，且该作动器自带激光位移传感器(实时测量伸缩量)，其中，一端的消隙球铰连接运动平台，另一端的消隙球铰固定在支座上，具体结构如图1所示.

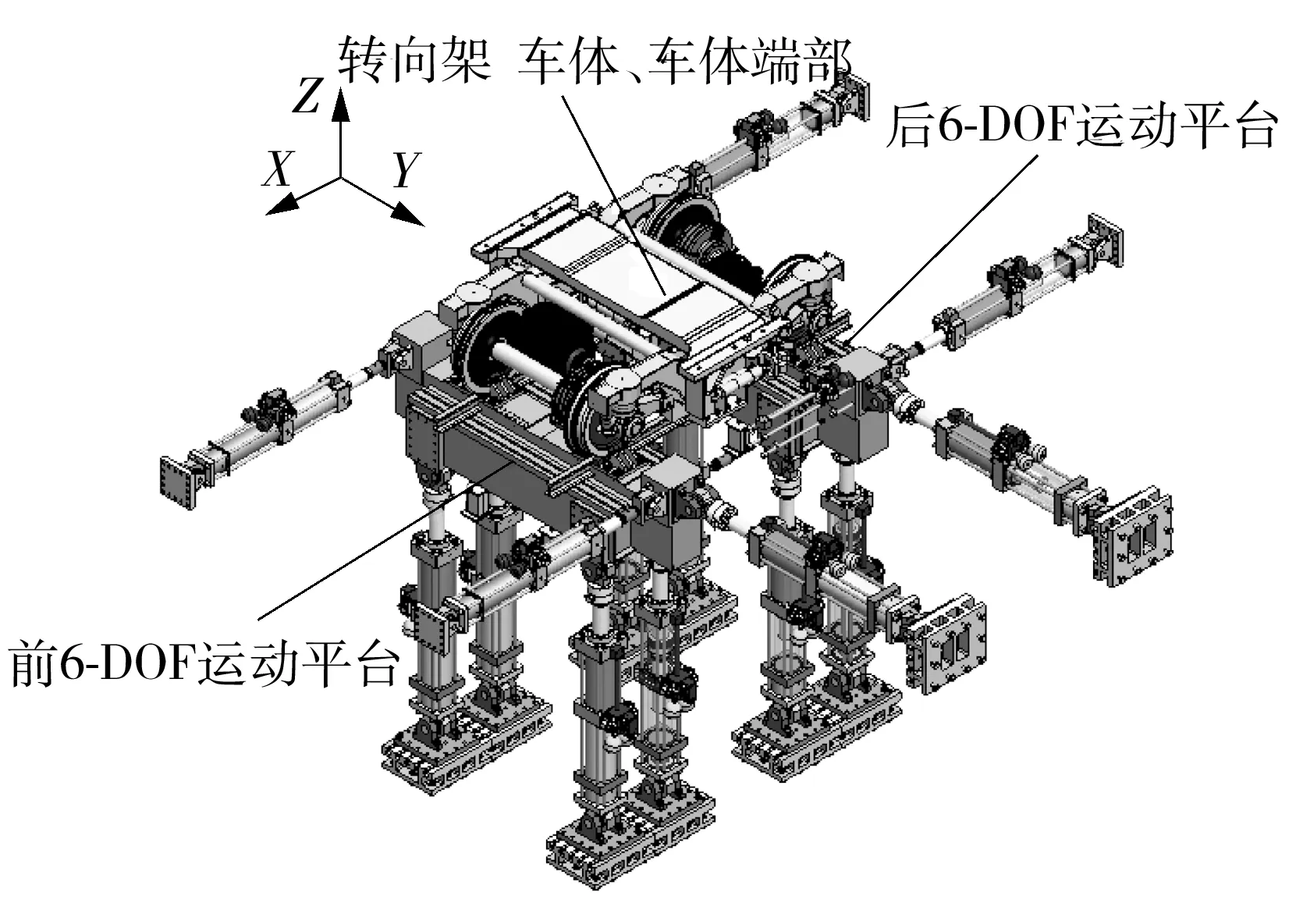
图1 转向架参数测定试验台Fig.1 Test bench for bogie parameters

14个作动器按照不同运动要求下位姿反解得到的伸缩量控制指令运动从而驱动试验台运动，进而模拟转向架、车体及车端部件在指定运动轨迹或实际轨道上的运行状态.

1.1 自由度与耦合度分析

前6-DOF运动平台子系统与后6-DOF运动平台子系统机械结构完全一致，且对称布置.以前6-DOF运动平台子系统为例，对其自由度进行详细分析.前6-DOF运动系统的活动构件总数n=1+7+7=15；运动副总数m=7+7+7=21；每根作动器两端采用消隙球铰连接，液压杆自身轴线的自转为局部自由度[5]ft=7，机构中的运动副自由度总和计算式为

(1)

式中,ui为第i个运动副的约束数，F为子系统自由度总和，文中F=6，子系统的自由度数为6.

该子系统的输入为7个电液伺服作动器的伸缩量，输出为运动平台的6个位姿参数(包括3个平移量、3个旋转量).位姿参数的输出不止取决于单个作动器的伸缩量，同时受所有输入量的影响，这种一个输入影响多个输出或者一个输出受多个输入影响的现象称为耦合.依据速度雅克比矩阵[7-8]中无0元素，因此判定该并联机构为完全耦合情形.

2 运动学建模

2.1 位姿反解

结合图2前6-DOF运动平台子系统的几何构型，选取前6-DOF运动平台中心为静坐标系原点O1，图2与图1中坐标轴的选取方向完全一致，且作动器的编号如图2所示,A代表7个作动器上铰链点及其坐标矩阵,B代表7个作动器下铰链点及其坐标矩阵.

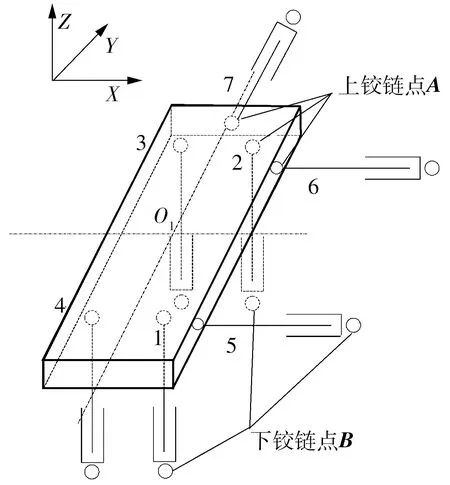
图2 前6-DOF运动平台结构图Fig.2 Mechanical view of forward 6-DOF kinematics platform

TZYX=

(2)

式中,TZYX表示齐次变换矩阵,c表示cos,s表示sin.

前6-DOF运动平台绕静坐标系原点O1进行位姿变化后(绕坐标轴旋转或沿中心点平移)，利用空间变换矩阵TZYX实现体坐标系与静坐标系的转化，进而得到同一静坐标系下的坐标值.空间变换过程

表示为

A′=TZYXA

(3)

至此,前6-DOF运动平台子系统中作动器上铰链点坐标A和平台下铰链点坐标B均转换到同一静坐标系下，由此连接上、下平台铰链点的7个作动器的伸缩量可根据上下铰链点间的距离公式确定，对应7个作动器的伸缩量Li：

Li=‖TA′-B‖,i=1,2,…,7

(4)

详细的前6-DOF运动平台位姿反解模型Simulink建模如图3所示.

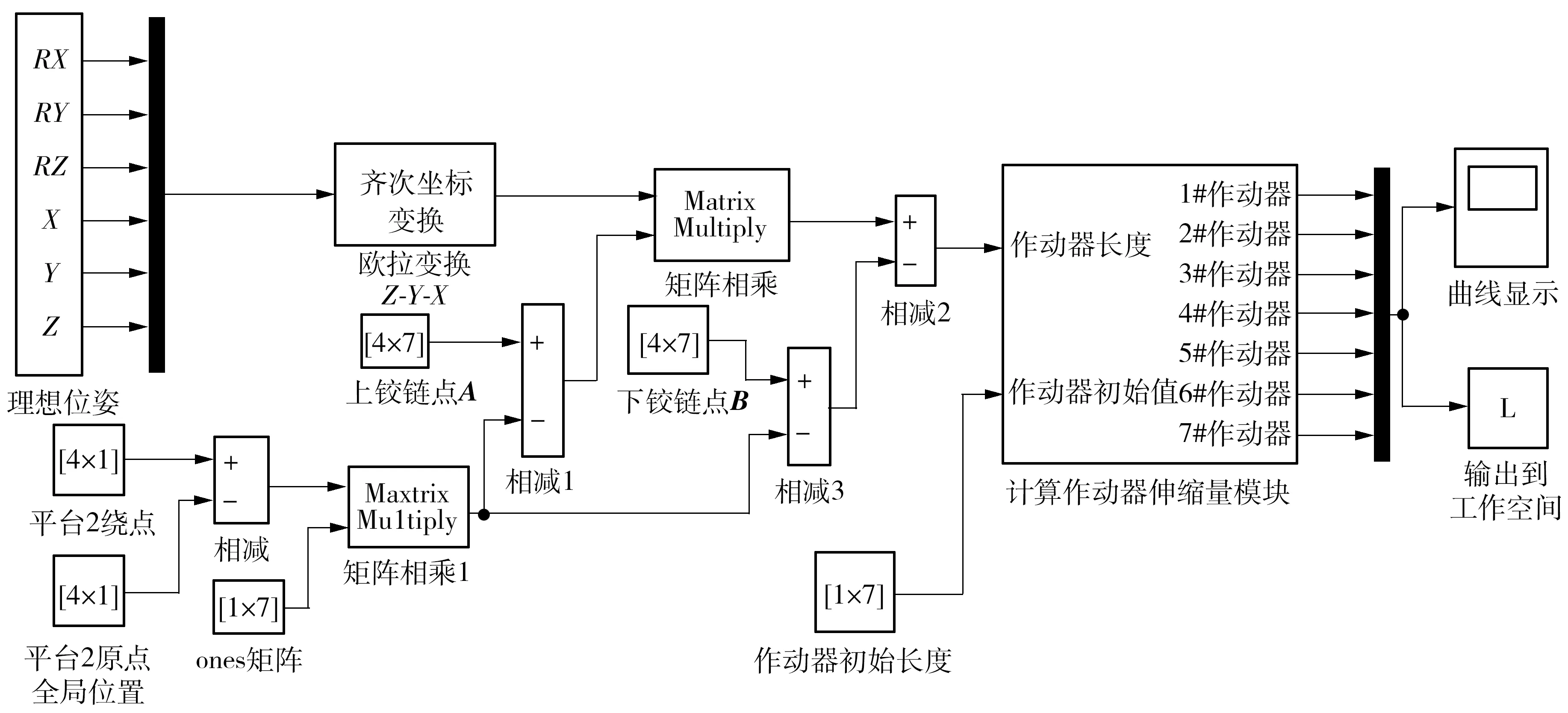
图3 位姿反解建模与仿真Fig.3 Modeling and simulating analysis of inverse kinematics

2.2 位姿正解

已知每个运动平台的6个位姿参数 ,通过空间位姿坐标变换和距离公式求得7个作动器伸缩量的过程称为位姿反解；而已知7个作动器的伸缩量求解每个运动平台的6个位姿参数的过程称为位姿正解.为了方便计算位姿，将7个作动器的长度值等效为

(5)

式中,f表示假设的非线性函数.式(5)为一组非线性方程组.

针对上述非线性方程组[10],传统数值解法Newton-Raphson迭代法编程易于实现，但其对初值具有较强的依赖性，初值选取不当会严重影响算法的收敛速度和误差性能.因此，文中提出了一种性能良好的基于L-M算法的改进BP[11-12]分类神经网络模型，将其与高阶收敛改进Newton-Raphson迭代法相结合来求解试验台位姿正解.文中提出的改进神经网络模型特别针对神经网络中输入层和输出层单元数较多、且输出层的元素之间数量级相差极大的问题，按照输出层的单元类型的不同进行分类网络训练，充分借助神经网络强大的非线性映射逼近能力，预测其位姿量初值.

3 混合策略求解及仿真分析

3.1 基于L-M算法的改进BP分类神经网络模型

神经网络都是由输入层、隐含层和输出层3部分构成，其中隐含层可设置为单层或多层.而一个3层的BP网络[13]可以实现任意n维到m维的映射.

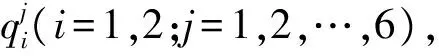
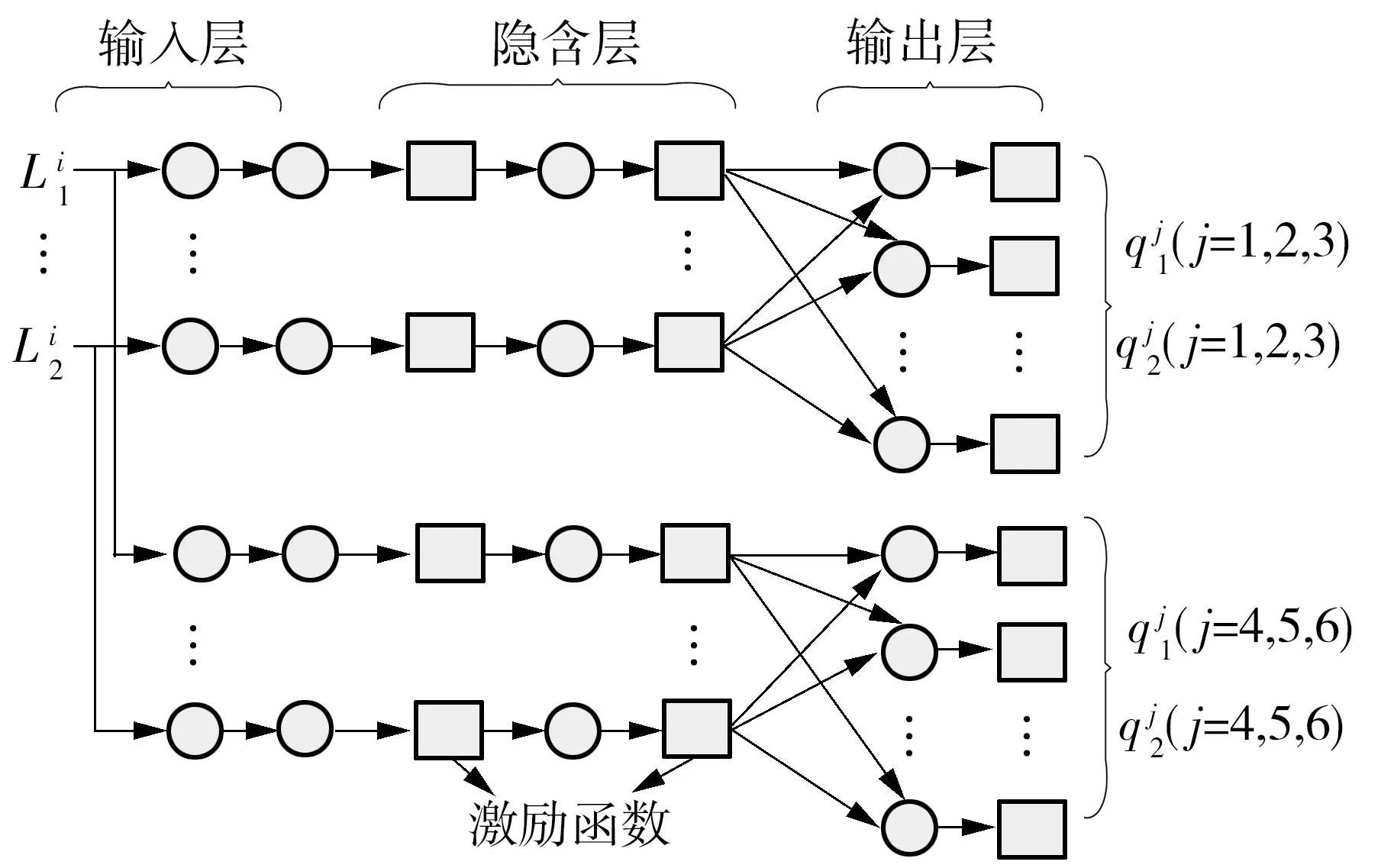
图4 基于L-M算法的BP分类神经网络结构Fig.4 Structure diagram of BP Neural network based on L-M algorithm

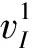
(6)

牛顿法是最速下降法的优秀代表，具有收敛快的优点，但是需要计算误差性能函数的二阶导数，且计算过程较为复杂，如果Hessian矩阵为非正定，可能由于搜索方向错误导致无法正常求解.因此，文中提出基于L-M算法的BP分类神经网络模型，此模型可以在修正速率时避免计算Hessian矩阵.

3.1.1 网络构建

采用基于L-M算法的BP分类神经网络模型进行下部双6-DOF运动平台位姿正解的初值预测.将大量样本数据作为训练数据.样本选取在运动平台的工作空间之内，同时先借助SolidWorks/Motion进行验证，保证选取样本值的准确性与可达性.样本训练过程如下：

1) 初始化神经网络的权值与阈值，利用Matlab中的rand和sort函数将1 000组样本数据随机选取800组作为训练数据，剩下的200组作为测试数据.

2) 由于运动平台的工作空间沿坐标轴平移位移量波动范围为100～300 mm，而绕坐标轴选择的角度弧度值应小于0.5 rad，角度值与位移量之间存在3个数量级，为了防止神经网络在函数逼近预测位姿量的过程中出现大数吃小数的问题，对所有神经网络按照输出层元素类型不同进行分类，从而达到精准训练网络，进而提升训练的有效性及精度.

3) 设置最大迭代次数为1 000次，期望值与输出值误差为4×10-12，当网络预测输出误差达到规定要求时，停止训练.

3.1.2 仿真结果分析

为了进一步验证基于L-M算法对非线性预测的情形，选取其他算法与之对比，包括SCG算法和BFGS算法.图5(a)为基于L-M算法的改进分类神经网络模型误差性能分析图，网络训练模型耗时3 s，迭代次数为30次，预测输出对比期望数据误差为4.211 6×10-12；图5(b)为基于BFGS算法的神经网络误差性能分析，网络训练模型耗时5 s，迭代次数278次，预测输出对比期望数据误差为1.675 2×10-7；图5(c)为基于SCG算法的神经网络误差性能分析，网络训练模型耗时1 s，迭代次数为345次，预测输出对比期望数据误差为6.524 7×10-6.

结合图5、6可知，L-M算法的收敛速度最快，如果要求的精度比较高，则该算法的优点尤其突出；SCG 算法应用于函数逼近问题时，由于不需要在每一次迭代中进行线性搜索，收敛速度与L-M算法相近，但L-M算法是针对中等规模的神经网络(多达数百个连接权)而提出的最快速算法，SCG算法在大型网络规模上性能要优于L-M算法；BFGS算法由于在每次迭代过程中都必须计算相应矩阵的逆矩阵，因此运算量随着网络规模的增大成几何级数增长，计算速度较之于L-M和SCG算法慢.因此，基于L-M算法的改进分类神经网络在误差性能、网络泛化能力、收敛速度与运行时间上均优于BFGS、SCG算法，图6从位移值和角度值方面进行了算法验证.综上所述，文中提出的基于L-M算法的BP分类神经网络模型能够求解位姿正解初值，且具有较好的实时性和精准性.

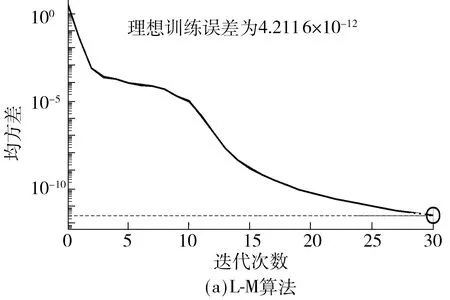
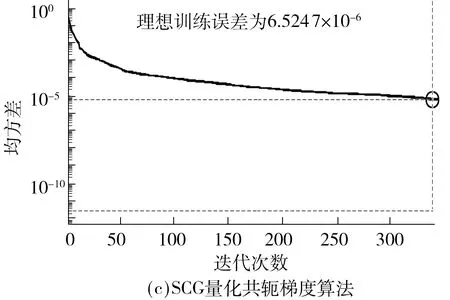
图5 误差性能分析Fig.5 Error performance analysis

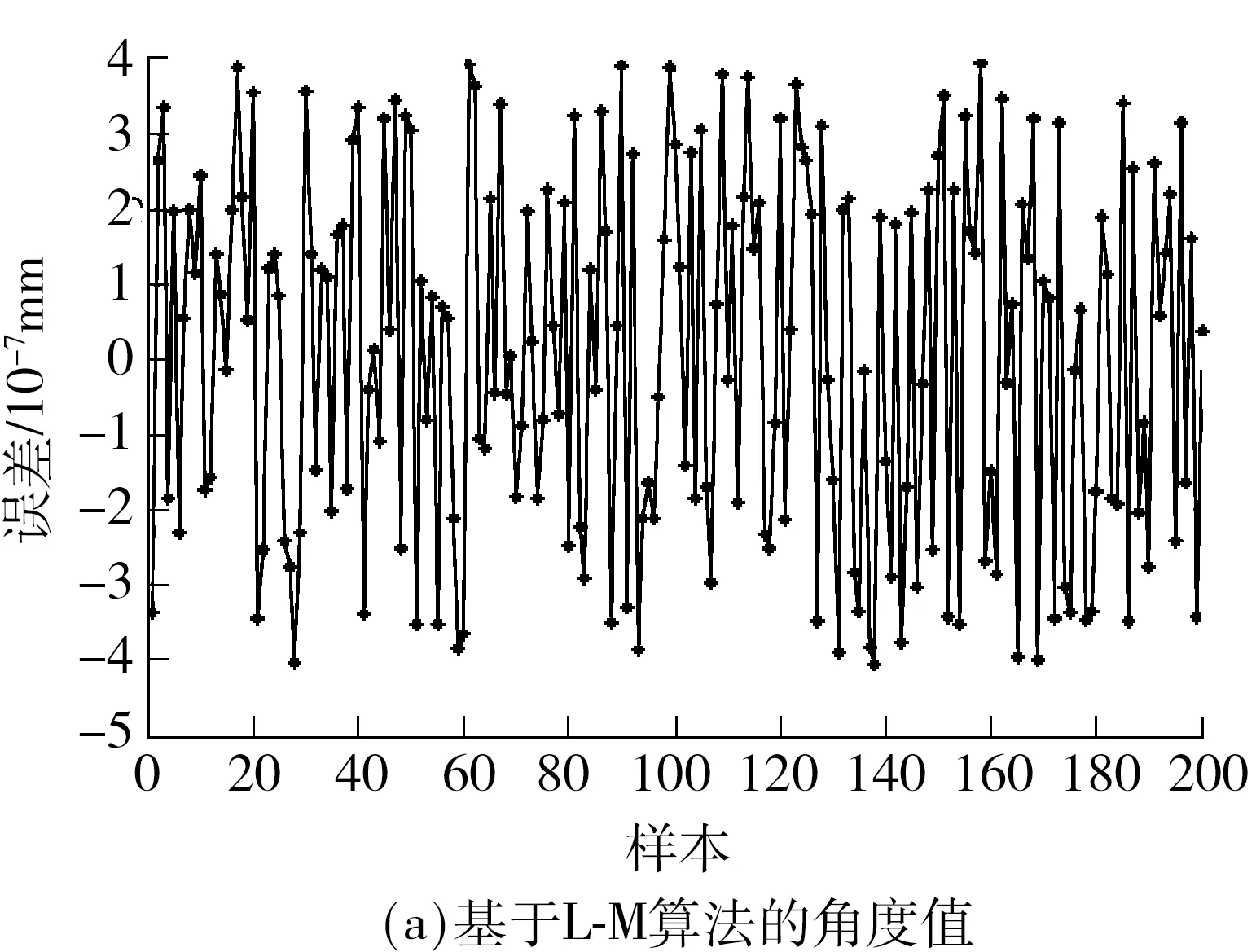
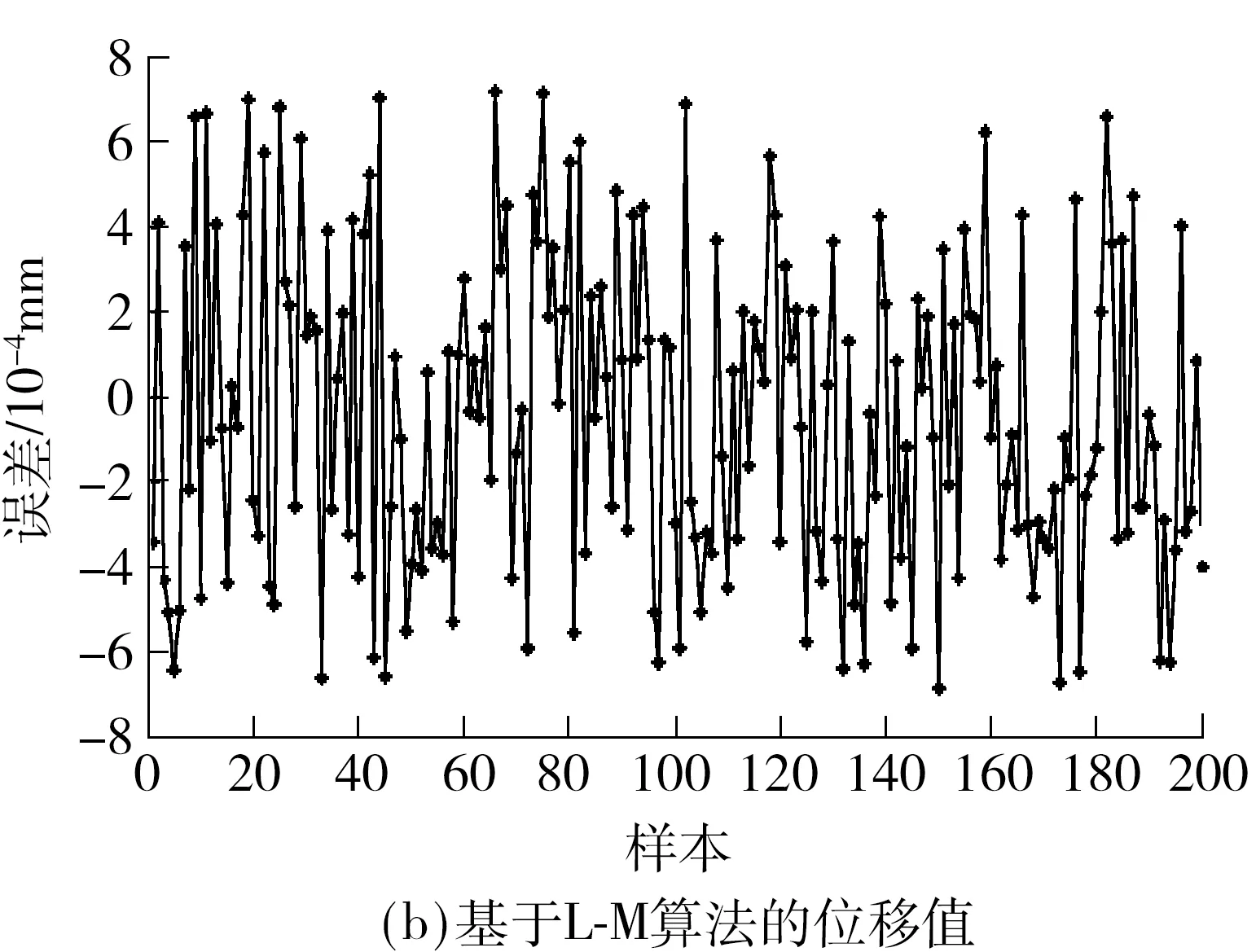
图6 网络预测误差Fig.6 Network prediction error

3.2 高阶收敛Newton-Raphson迭代法

为了最大限度地提高位姿正解的求解速度和精度，使计算机将大量的时间用在控制模型上.Darvishi等[13]和Daftardar-Gejji等[14]采用Adomian分解方法提出一个三阶收敛的数值迭代方法.Waseem等[15]采用新型的分解方法，推导出一系列高阶迭代方法.文中提出基于L-M算法的改进BP分类神经网络结构模型和高阶收敛的改进Newton-Raphson迭代法(HMNR)相结合的混合策略(HS)求解试验台位姿正解.迭代格式如下：

(7)

(k=0,1,2,…)

迭代的终止条件为

‖X(k+1)-X(k)‖∞=max(x1,x2,…,xn)≤Emax

(8)

4 试验验证

4.1 车端台架试验

文中选取实际线路(s弯-R180夹直线)轨道谱路谱数据进行位姿反解，求解14个作动器的伸缩量.将14个伸缩量指令加载到作动器上驱动试验台运动，进而动态模拟相邻车端端部在实际轨道线路上运行的工况.如图7所示，在转向架参数测定试验台上分别固定相邻的两节车端部件，包括风挡、车钩、万变式端墙等.在车端部风挡内部中下位置安装车端位姿测量装置，测量装置中配备旋转编码器及激光位移传感器便于测量车端相对位姿量(包括位移量与旋转量)，与此同时，在万变式端墙上布置大量的超声波测距传感器，用于测量车端错距及车端端墙之间限值.实验连续进行两个周期，随着试验台运动，车端部件也随之运动，从而测得轨道车辆车端部之间在实际运动过程中的相对位姿变化.

图7 转向架参数测定试验台及车端位姿测量装置Fig.7 Test bench for bogie parameters and vehicle position and attitude measurement system

4.2 试验结果分析

如表1所示，在不同的迭代终止条件下，将NR、HMNR和文中提出的HS方法进行对比，可知在同一终止条件下，HS方法在迭代次数上较之NR方法减少了41%，在迭代时间上缩短了23%；较之单一高阶HMNR方法，在迭代次数上减少了7%，在迭代时间上缩短了8.2%.不管是在运行时间上，还是迭代次数上，文中提出的混合策略HS方法都有很大优势，完全满足实时性要求.

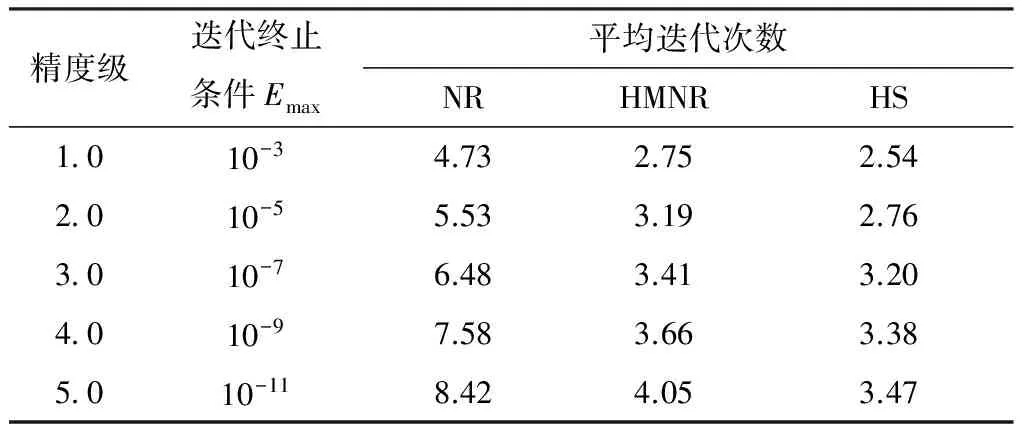
表1 3种方法下的平均迭代次数Table 1 Average iteration number of the three methods

如图8所示，3号平台相对于2号平台沿X、Y、Z轴位移和绕X、Y、Z轴旋转角度的实测数据与理论计算数据对比结果，除沿Z轴位移量较小时的误差较大外，其余实测数据与理论计算数据结果较为接近；沿X轴位移最大绝对误差为0.996 mm，相对误差为8.66%，沿Y轴位移最大绝对误差为10.69 mm，最大值的相对误差仅为2.78%；沿Z轴位移最大绝对误差为2.34 mm，最大值的相对误差为8.78%；绕X轴夹角最大绝对误差为0.04°，相对误差为0.53%；绕Y轴夹角最大绝对误差为0.05°，相对误差为0.63%；绕Z轴夹角最大绝对误差为0.17°，相对误差为34.34%.

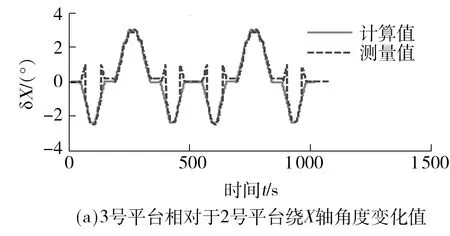
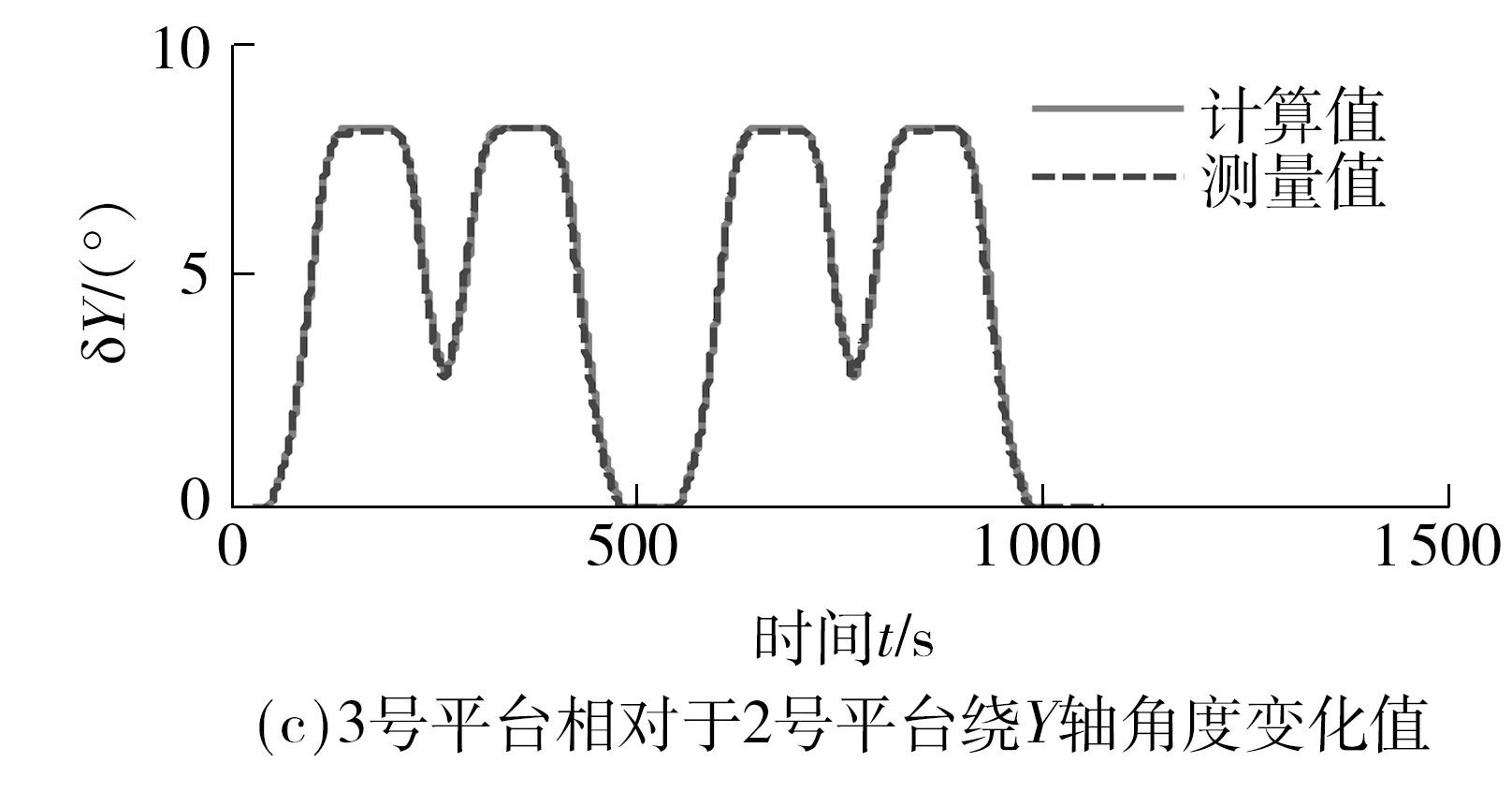
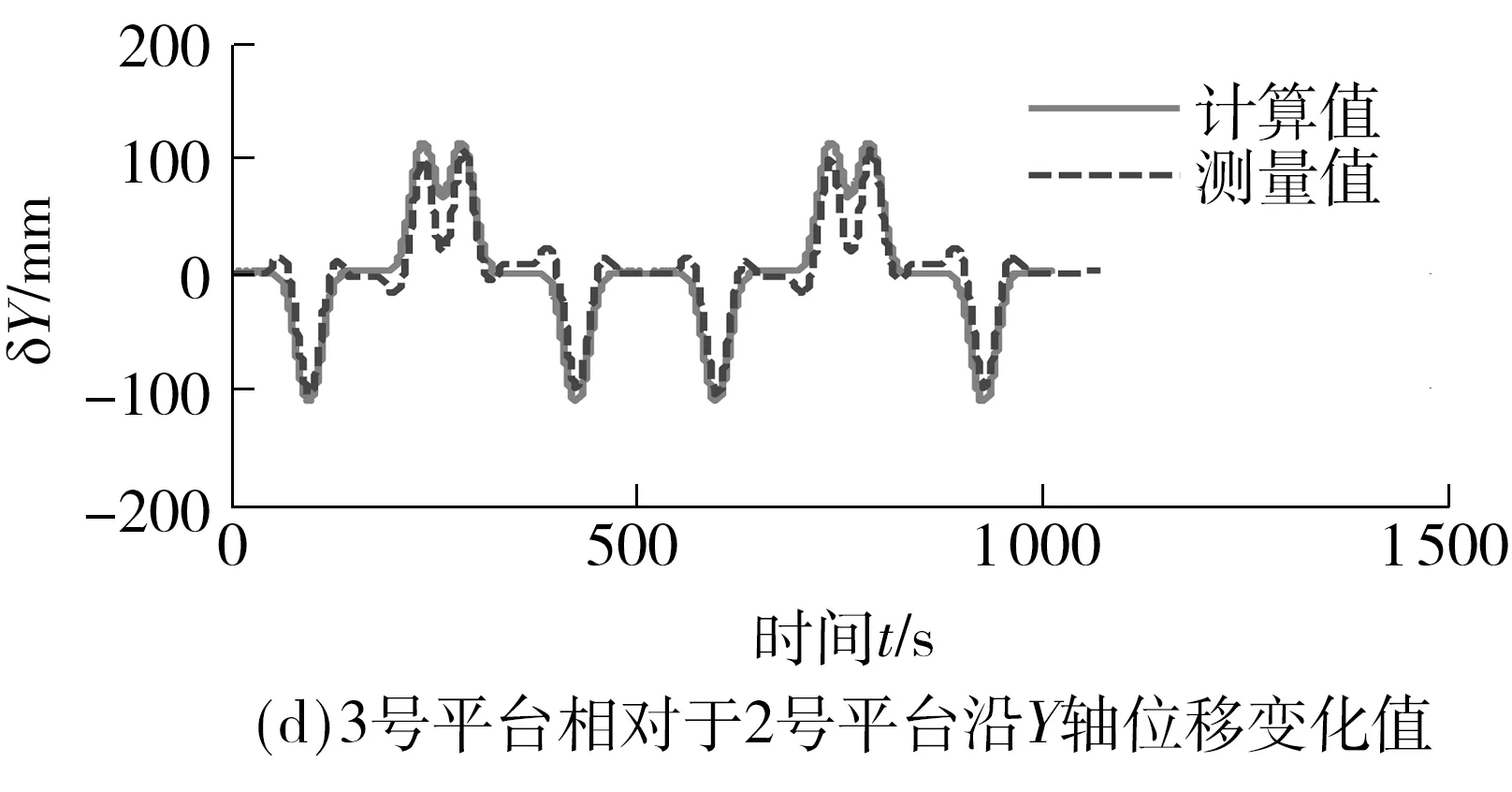
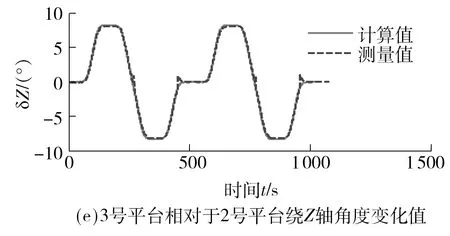
图8 车端相对位姿实测值与计算值对比Fig.8 Comparison of measured value and theoretical value of the relative position and attitude of the vehicles

对比图9所示计算值和测量值可得：(1)绕X、Y、Z轴的旋转角度值均低于8°(0.139 6 rad)，沿Y轴位移值达到100 mm.分析轨道路谱数据可知，轨道整体处于水平面，且其转弯半径设计达到极限半径180 m，因此轨道车辆在经过圆曲线时沿Y轴平移出现了极大的位移值.文中提出基于L-M算法的改进BP分类神经网络结构模型，针对这种位移值与角度值差别很大的情况设定分类，这样既可以保证运算时间，又可保证运算精度.(2)受车端位姿测量系统精度所限，对比实测值和计算值可知，实测值越大精度越高，实测值减小精度反而下降.

5 结语

并联机构位姿正解的实时性和可靠性一直是个难题.文中提出基于L-M算法的改进BP分类神经网络结构模型与高阶收敛改进Newton-Raphson迭代法HMNR相结合的混合策略HS求解并联机构位姿正解.以转向架参数测定试验台为例，借助位姿反解将轨道谱路谱转化成试验台作动器的伸缩量，从而驱动试验台耦合运动模拟真实车体在实际线路上的运行状态.运用大量的样本数据作为训练数据，实现了试验台位姿正解的初值求解，并与常用的基于拟牛顿算法BFGS的神经网络模型和量化共轭梯度算法SCG的神经网络模型进行对比分析.结果表明，L-M算法模型在误差性能分析上明显优于BFGS拟牛顿与SCG算法模型，且预测角度值误差均小于4×10-7,位移值误差均小于8×10-4.将网络预测值作为HMNR法的初值，进行迭代计算，较之Newton-Raphson(NR)法，迭代次数减少了41%，迭代时间缩短了23%；较之单一高阶HMNR方法，迭代次数减少了7%，迭代时间缩短了8.2%.将此混合策略HS用于试验台，进行实际相邻车端相对位姿测量试验，进一步验证了混合策略的有效性.

综合考虑，文中提出的HS方法不论是在运行时间上，还是在迭代次数上，均大大提高了位姿正解的求解精度与速度，满足实时性的要求，且能够为6-DOF运动平台位姿大闭环控制、故障恢复、工作空间分析、试验过程的实时监控等奠定基础.

[1] 王兴宇，苏建，梁树林.用于转向架刚度测试的6自由度加载平台控制策 [J].大连交通大学学报，2010，31(5)：14-20．

WANG Xing-yu,SU Jian,LIANG Su-lin.Study of bogie stiffness test control strategy for six-DOF loading plate [J].Journal of Dalian Jiao tong University，2010，31(5):14-20.

[2] 李磊.六自由度并联平台位置正解与控制方法研究 [D].哈尔滨:哈尔滨工程大学,2008.

[3] 王秀刚,苏建,曹晓宁.基于旋转矩阵正交性的转向架6自由度平台位姿正解解算 [J].吉林大学学报(工学版),2013,43(5):1241-1246.

WANG Xiu-gang ,SU Jian，CAO Xiao-ning.Forward kinematics solution of bogie 6-DOF platform based on the orthogonality of rotation matrix [J].Journal of Jilin University(Engineering and Technology Edition),2013,43(5):1241-1246.

[4] GHASEMI A,EGHTESAD M,FARID M.Neural network solution for forward kinematics problem of cable robots [J].Journal of Intelligent & Robotic Systems,2010,60(2):201-215.

[5] 沈惠平,尹洪波,王振.基于拓扑结构分析的求解6-SPS并联机构位置正解的研究 [J].机械工程学报,2013,49(21):70-80.

SHEN Hui-ping,YIN Hong-bo,WANG Zhen.Research on forward position solutions for 6-SPS parallel mechanisms Based on Topology Structure Analysis [J] Journal of Mechanical Engineering,2013,49(21):70-80.

[6] 尹洪波,沈惠平,邓嘉鸣,等.球面并联机构的结构降耦及其位置正解求解 [J].机械科学与技术,2015,34(1):51-55.

YIN Hong-bo,SHEN Hui-ping,DENG Jia-ming,et al.The reducing in structure coupling and the forward position analysis for the spherical parallel mechanisms [J].Mechanical Science and Technology for Aerospace Engineering,2015,34(1):51-55.

[7] 张彦斌,吴鑫,刘宏昭.无耦合3自由度并联机构的设计与分析 [J].农业机械学报,2008,39(8):208-210.

ZHANG Yan-bin,WU Xin,LIU Hong-zhao.Design and analysis of a 3-DOF non-coupled parallel manipulator [J].Transactions of the Chinese Society for Agricultural Machinery,2008,39(8):208-210.

[8] 张彦斌,刘宏昭,吴鑫,等.2T1R弱耦合并联机构的运动学和奇异性分析 [J].农业机械学报,2008,39(4):132-136.

ZHANG Yan-bin,LIU Hong-zhao,WU Xin,et al.Kinematics and singularity analysis of a novel weakly-coupled parallel manipulator [J].Transactions of the Chinese Society for Agricultural Machinery,2008,39(4):132-136.

[9] 杨永刚,赵杰,刘玉斌.6-PRRS并联机器人正运动学求解 [J]吉林大学学报(工学版),2008,38(3):731-734.

YANG Yong-gang,ZHAO Jie,LIU Yu-bin.Solving forward kinematics of 6-PRRS parallel robot [J].Journal of Jilin University (Engineering and Technology Edition),2008,38(3):731-734.

[10] 朱坚民,沈正强,李孝茹.基于神经网络反馈补偿控制的磁悬浮球位置控制 [J].仪器仪表学报,2014,35(5):976-986.

ZHU Jian-min,SHEN Zheng-qiang,LI Xiao-ru.Magnetic levitation ball position control based on neural network feedback compensation control [J] Chinese Journal of Scientific Instrument,2014,35(5):976-986

[11] 何伟铭,宋小奇,甘屹.传感器校正的优化灰色神经网络建模方法研究 [J].仪器仪表学报,2014,35(3):504-512.

HE Wei-ming,SONG Xiao-qi,GAN Yi.Research on optimized grey neural network modeling method for sensor calibration [J] Chinese Journal of Scientific Instrument,2014,35(3):504-512.

[12] 丁硕，巫庆辉.基于改进 BP 神经网络的函数逼近性能对比研究 [J].计算机与现代化，2012(11):10-13.

DING Shuo,WU Qin-hui.Performance comparison of function approximation based on improved BP neural net-work [J].Computer and Modernization,2012(11):10-13.

[13] DARVISHI M T,BARATI A.A third-order Newton-type method to solve systems of nonlinear equations [J].Applied Mathematics and Computation,2007,187(2):630-635.

[14] DAFTARDAR-GEJJI V,JAFARI H.An iterative method for solving nonlinear functional equations [J].J Math Anal Appl,2006(316):753-763.

[15] WASEEM M,NOOR M A,NOOR K I.Efficient method for solving a system of nonlinear equations [J].Applied Mathematics and Computation,2016,275:134-146.

Supported by the National Natural Science Foundation of China(51575232)

ForwardKinematicsofTestBenchforBogieParameters

WANGQi-mingSUJianNIUZhi-huiLINHui-yingXUGuan

(School of Transportation, Jilin University,Changchun 130025, Jilin, China)

The existing Newton-Raphson iterative method used for the forward kinematics of parallel mechanisms has a strong dependency on the initial value with a slow iteration convergence speed, and thus the instantaneity cannot be satisfied. In order to solve these problems, a combinatorial method of a new improved BP Neural Network model based on the Levenberg-Marquardt algorithm and the high-order modified Newton-Raphson (HMNR) iteration method is proposed to achieve the forward kinematics of Redundancy parallel mechanism. Then, by taking a test bench for bogie parameters (TBBP) as the example, the track spectrum is converted to the displacement of the actuator with the help of the invert kinematics.Hydraulic system

the instruction of displacement to propel the test bench’s coupling motion,which is used to simulate the running status of the real vehicle or bogie on real tracks.By using a mass of actual data as the training material, the initial value of the forward kinematics of the test bench is thus determined, which is then compared with those obtained through the neural network models respectively based on the quasi-Newton algorithm BFGS and the scaled conjugate gradient (SCG) algorithm. Experimental results show that the L-M algorithm model is obviously superior to the BFGS algorithm model and the SCG algorithm model in terms of the error performance analysis, with a predicted angle value of less than 4×10-7and a displacement error of less than 8×10-4. In addition, the predicted value is taken as the initial value of the HMNR method to perform an iterative calculation, which causes a 41% reduction in the required iterations and a 23% reduction in the iteration time in comparison with the Newton-Raphson(NR) method. Finally, by applying the hybrid strategy on the TBBP for testing the relative position and attitude of adjacent vehicles, the effectiveness of the hybrid strategy is further validated.

railway vehicle;forward kinematics;redundancy;6-DOF parallel mechanism; Levenberg-Marquardt algorithm;higher-order convergence

2016-07-22

国家自然科学基金资助项目(51575232)；吉林省科技厅重点科技攻关项目(20160204018GX)

王启明(1991-)，女，博士生，主要从事车辆智能化检测研究.E-mail:wang.qiming2008@163.com

†通信作者:林慧英(1974-)，女，博士生，讲师，主要从事车辆智能化检测研究.E-mail:sujianjd@163.com

1000-565X(2017)08-0042-08

U 260.14+6

10.3969/j.issn.1000-565X.2017.08.007