OD约束的出租车经验模型与路径规划*
潘晓芳 周顺平 杨林 万波
(1.中国地质大学(武汉) 信息工程学院,湖北 武汉 430074;2.信阳师范学院 地理科学学院,河南 信阳 464000)
OD约束的出租车经验模型与路径规划*
潘晓芳1,2周顺平1†杨林1万波1
(1.中国地质大学(武汉) 信息工程学院,湖北 武汉 430074;2.信阳师范学院 地理科学学院,河南 信阳 464000)
从出租车轨迹中提取司机经验并应用于大众出行引导是出租车轨迹数据的重要应用领域.在经验提取上,为了避免传统方法中因忽视OD而导致结果不准确的问题,提出了OD约束的经验模型(ODCEM).以深圳市为例,分别用传统的经验模型、ODCEM及最短路径模型进行实验.结果显示:ODCEM在经验提取和路径推荐时能够成功地模拟出租车司机的经验;3种方法的比较中,ODCEM推荐的路径在通行时间和平均通行速度上体现出93.3%和76.7%以上的优势,通行长度位于其他两种模型推荐的路径之间.最后对约束的尺度进行了讨论.结果显示,约束尺度为2 km×2 km时效果比较理想.
OD约束;出租车轨迹;经验模型;路径规划
随着科技的进步,大量的轨迹数据日益积累[1],据统计,93%的轨迹数据是有规律性和重复性的[2],这些轨迹数据为研究人类行为提供了基础素材.出租车轨迹是由安装在出租车上的传感器在移动过程中采样得到的GPS数据,近年来,利用出租车轨迹数据进行城市交通的研究日益增多.出租车司机长期频繁穿梭于城市的各个角落,很多时候,他们出行的线路往往比导航软件规划的路径更为优秀[2].所以,出租车司机的出行经验非常值得借鉴,学者已经在此方面开展了大量的研究[3-11].
从目前的研究来看,学者普遍将路径频繁出行[3]、经常走[4]、路段通行频次高[5-7]、路段平均通行次数[8-9]多、经常愿意走[10]等作为经验的认定和经验等级建立的标准,而经验提取方法则通过将全部出租车轨迹与路网进行匹配,然后统计每条道路上出租车轨迹的数目(即通行总频次),以此作为该道路的经验值大小.这种方法能够反映城市道路的交通状况,但是缺少对出行起止地的考虑,不同的出发地(Origin)和目的地(Destination)(简称OD)对司机线路的选择至关重要,在没有考虑出行OD的情况下,道路上的通行总频次(即道路的交通流量)受诸多因素的影响,例如Jiang[11]认为城市中有良好连通性和处于中心地位的路段流量较大,吴健生等[12]研究发现,等级高、位于城市中心的路段交通流量大,辛飞飞等[13]认为出租车在路网上的覆盖强度具有明显的时变规律,另外,城市功能区类型、人口密度等因素也是道路交通流量的重要影响因素.而实际上,在确定出行OD后,与该OD方向无关的道路就与本次出行没有任何关系(即使其通行总频次很高).因此,在利用出租车轨迹提取经验的过程中,如果能够对起止点进行有效的约束,将会提高经验的准确性.
文中的研究重点就是基于出租车轨迹数据,构建基于OD约束的经验模型(ODCEM),并进行相应的出行路径规划.
1 基本思想和定义
1.1 基本思想
文中的技术路线如图1所示,分为4个阶段.第1阶段是对出租车轨迹数据的预处理.由于地面建筑物的遮挡及设备的不稳定性,可能会导致部分GPS信号异常,因此轨迹记录存在一些重复、漂移、速度及时间错乱甚至数据丢失等问题;另外,由于出租车车辆异常、驾驶员操作不当等,也会产生一些异常记录.因此,数据预处理阶段主要是去除各种情况下的异常记录.第2阶段是地图匹配.由于GPS误差,收集到的轨迹点并没有完全落在道路上,因此需要进行地图匹配,建立出租车轨迹与对应道路的关系.第3阶段是路网重建.通过文中提出的模型,计算道路上的出租车的通行频次、通行时间及路段长度等基本信息,构建经验道路网络.第4阶段是路径推荐,在新的经验路网下,根据Dijkstra算法,为用户推荐OD约束下的经验路径,并进行有效性验证.
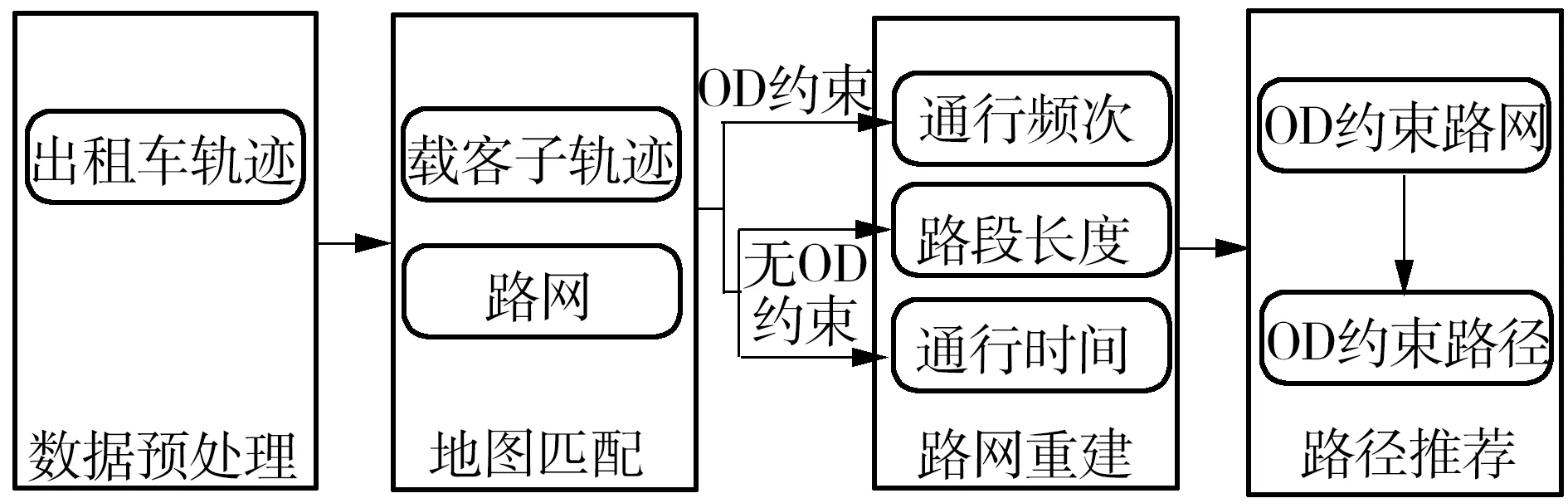
图1 技术线路Fig.1 Technical route
1.2 基本定义
定义1 轨迹(Trajectory).轨迹由安装在出租车上的GPS在出租车运动过程中产生的一系列随时间变化的点组成,Trajectory={p1,p2,…,pn},其中每个点pi一般由出租车车牌号、地理坐标(经度,维度)、时间、载客状态、速度、方向等信息组成,即pi=(ID,VEHICLENUMBER,LON,LAT,DATE,DIRECTION,SPEED,FLAG).
定义2 子轨迹(Trip).根据出租车在运动过程中是否载客可将其轨迹划分为载客轨迹和空载轨迹,每次上客点到下客点之间的载客轨迹的集合为一个子轨迹,即Trip={p1,p2,…,pn|∀pi·FLAG=LOAD,1≤i≤n},其中n表示子轨迹包含点的个数,pi·FLAG为第i个点的载客状态,LOAD表示载客,EMPTY表示空载.
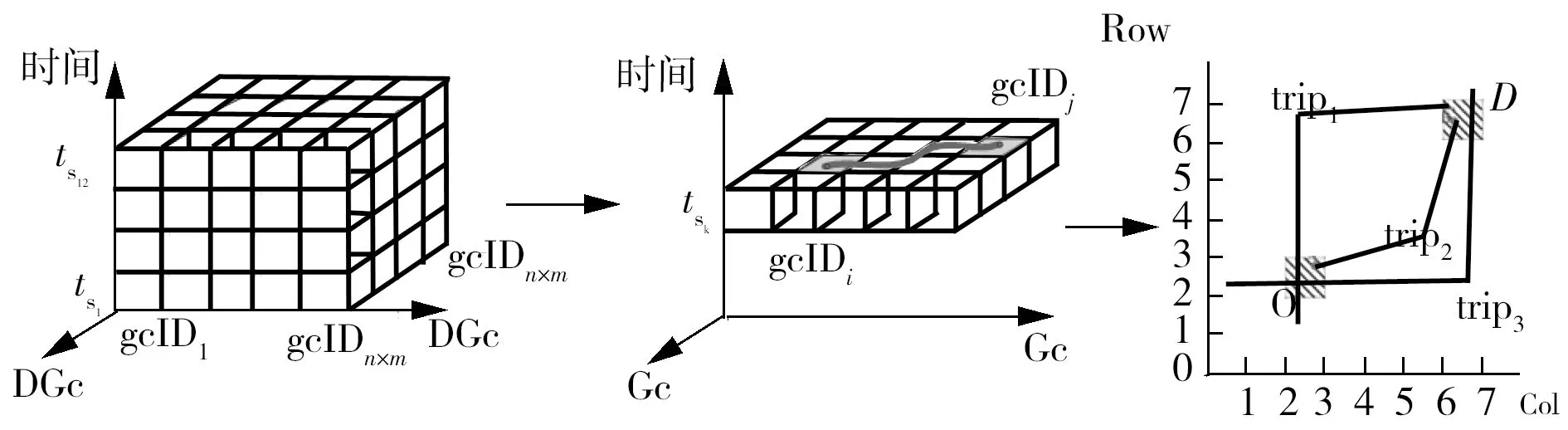
如图2所示,假设一条出租车轨迹Trajectory={p1,p2,…,p19},实心点表示载客点,空心点表示空载点,则其子轨迹为trip1,trip2和trip3.
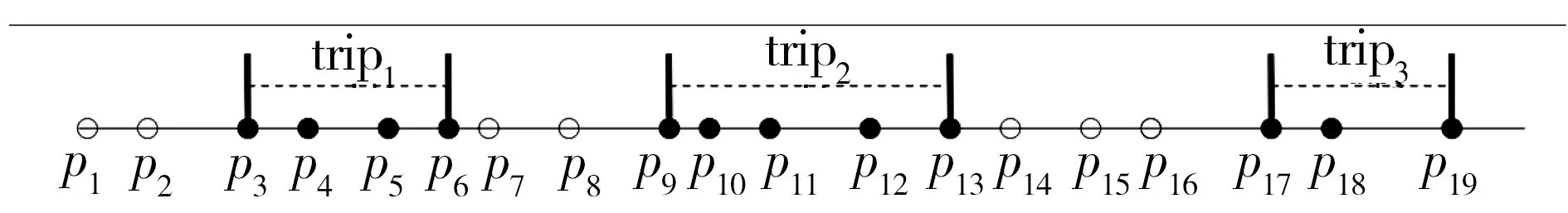
图2 子轨迹划分Fig.2 Division of sub-trajectory
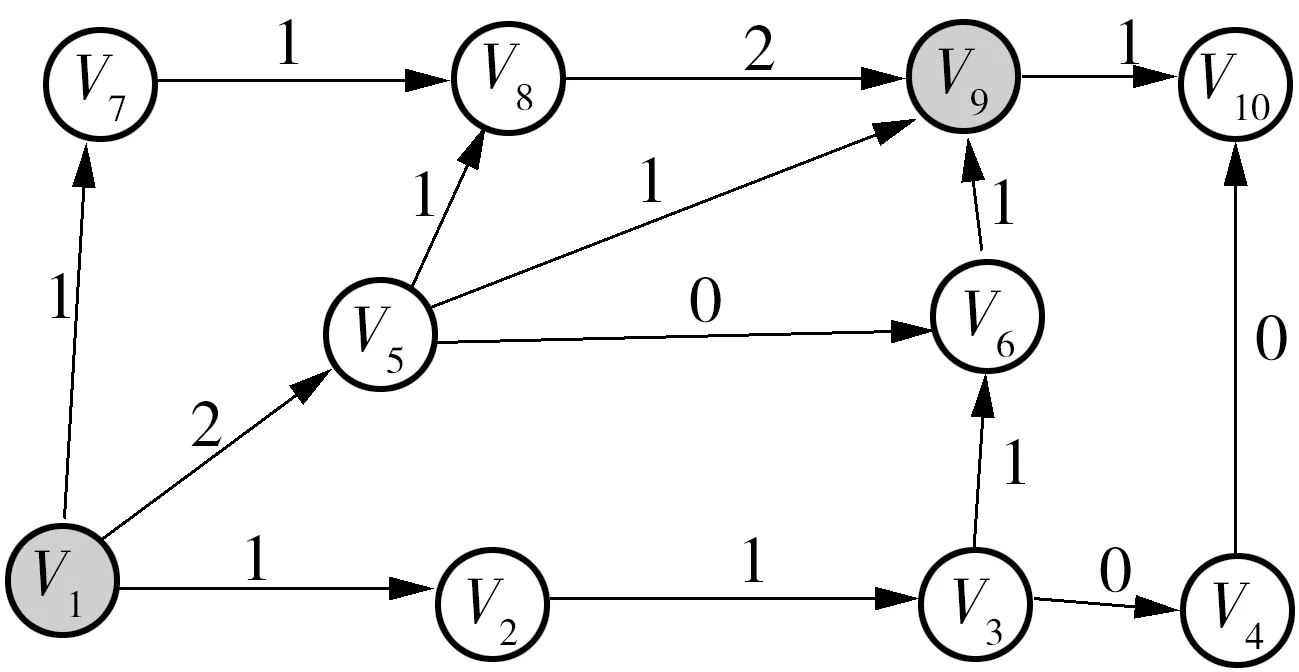
定义3 OD约束下的轨迹(ODC-T).OD约束下的轨迹指的是经过限定的出发地、目的地的子轨迹集合.即ODC-Trajectory={trip1,trip2,…,tripm},其中tripk={p1,p2,…,pn|∃B(pi,O)∧B(pj,D),i 如图3所示,trip1,trip2,…,trip66条子轨迹经过的节点序列分别为trip1(V1,V2,V3,V6,V9)、trip2(V1,V2,V3,V4,V10)、trip3(V1,V5,V6)、trip4(V1,V5,V9)、trip5(V1,V5,V8,V9)和trip6(V1,V7,V8,V9,V10).假设节点V1和V9为约束的起止O、D,则OD约束下的轨迹分别为trip1、trip4、trip5和trip6. 图3 OD约束下的轨迹与路段经验Fig.3 Trajectory and segment experience of OD constraint 定义4 OD约束的路段经验(ODC-SE).指在OD约束下,路段Si上所有出租车的通行次数,也就是ODC-Trajectory经过路段Si的次数. 计算ODC-SE时,对每一条路段Si,判断ODC-Trajectory中的tripj是否经过Si,如果经过,则Si的路段经验值SEsi加1.判断tripj经过Si的方法是通过判断tripj中的轨迹点pk是否在Si上,如果tripj中存在任意一个轨迹点pk在路段pk上,tripj经过路段Si. 图3所示4条ODC-Trajectory中,trip1经过路段S1、S2、S5、S6;trip4经过路段S7、S9;trip5经过路段S7、S10;trip6经过路段S11、S12、S13、S14.根据定义5,路段S3、S4和S8上没有ODC-Trajectory,其路段经验为0,路段S7和S13上有两条ODC-Trajectory,其路段经验为2,其他路段的路段经验均为1. 定义5 经验路网(ERN).经验路网G=(V;S;SE),V为道路节点集合,S路段集合,SE为OD约束下的路段经验集合.图3区域对应的经验路网如图4所示. 图4 经验路网Fig.4 Experience network 在实际研究中很难实现任意两点之间经验的提取,因此,文中采用基于格网的方法,将研究区域进行正方形格网划分,每个网格表示一个约束区域O或D,得到一个空间矩阵Gridcell×Gridcell Matrix.为了研究不同时间的轨迹特征,在空间矩阵上增加时间维度,假设以T小时为基本单元,则一天被划分为24/T个轨迹段,从而构建OD约束的轨迹立方体(ODC-TC),如图5所示. 图5 轨迹立方体Fig.5 Trajectory cube 随时间推移的出租车轨迹可以用该ODC-TC进行模拟,ODC-TC中每个单元表示一个格网约束区域在时间段内的所有轨迹点集合,为研究方便,取T=2,将一天划分为12个时段,约束区域的大小在3.4节中讨论.这里先假设约束区域的边长为d,研究区域的范围为(Xmin,Ymin,Xmax,Ymax),则研究区平面将被划分为coln行、rown列,行、列的计算公式为 (1) (2) 因此,任意一点p(x,y)所在网格的行、列号为 (3) (4) 在确定研究区范围、约束点坐标及出行时间后,利用ODC-TC提取ODC-SE的过程如图6表示. 图6 提取ODC-SE的过程Fig.6 Process of extracting ODC-SE 建模主要思想为:首先,由式(1)、(2)得到研究区行列值;接着,在ODC-TC中提取所需要的轨迹点层,在该层内将约束点坐标利用式(3)、(4)转换为约束区域O、D的行列号;然后,根据定义3得到OD约束下的轨迹ODC-T;最后,根据定义4计算ODC-SE.算法描述如下. 算法名称:ODC-SE提取算法 算法输入:轨迹点文件(tp),道路线文件(road),起止地Po、Pd,时间段T 算法输出:OD约束的路段经验 算法描述: ∥子轨迹、时间轨迹层、OD约束轨迹的初始化 TrajectoryL=∅;TrajectoryT=∅;ODC-Trajectory=∅; 步骤1 根据式(1)、(2)计算区域的行、列值; 步骤2 根据式(3)、(4)计算约束起止地Po、Pd所在的行列号gcIDo、gcIDd while(tp!=NULL) if(pi==EMPTY)and(pi+1==LOAD) and (pn-1==LOAD)andpn==EMPTY) tripi={pi+1,…,pn-1} TrajectoryL=TrajectoryL∪{tripi}; 步骤3 while(TrajectoryL!=NULL) if((tripi·startdate>Tstart)and(tripi·enddate TrajectoryT=TrajectoryT∪{tripi}; 步骤4 while(TrajectoryT!=NULL) 对每一个tripi: if(pjin gcIDoandpkin gcIDd) ODC-Trajectory=ODC-Trajectory∪{tripi}; 步骤5 对road中的每个字段根据定义5计算路段经验. 在基于轨迹提取经验的研究中,学者普遍使用时间、距离、速度及经验认知[6-7,9]等来规划路径,因此,本研究也将路段经验、路段长度和路段通行时间作为OD约束的路段经验系数的主要影响因子. 路段的平均通行速度的计算不受约束条件的影响,应使用全部轨迹数据进行计算.Jiang等[14-15]使用浮动车数据对路段平均速度的计算做了详细的研究,路段Si上的平均通行速度为 (5) 式中,m表示统计时间段内路段Si上的通行的出租车总数,n表示路段Si上采样点个数,Δl表示两个采样点之间的距离,Δt表示两个采样点之间的时间. 路段Si的平均通行时间为 (6) 式中,LSi表示路段Si的长度,VSi表示路段Si上的平均通行速度. OD约束的路段经验系数表示为 CEPSi=w1×SESi+w2×LSi+w3×TSi (7) 其中,w1、w2、w3分别为权重系数,且w1+w2+w3=1.对式(7)进行归一化处理(根据研究区数据特点,路段经验、路段长度和通行时间的数量级别差异较大,因此对路段长度和通行时间进行了取对数操作): (8) 式中,SESmax与SESmin分别表示ODC-SE的最大值和最小值,LSmax和LSmin分别表示路段长度的最大值和最小值,TSmax和TSmin分别表示通行时间的最大值和最小值. 根据式(8)对路段的经验系数CEPSi的定义,路径推荐问题可以转换为:用户设定出行起止地后,采用最短路径算法[16]寻找一条路径route,使该路径的总经验值CEProute最小, (9) 由于OD约束后会出现大量路段没有轨迹的情况,即SESi=SESmin=0,因此路段的经验系数达到最大,即权重系数w1,此时,该路段的经验系数CEPSi主要由路段的长度及通行时间决定,即寻路的依据是路段长度和通行时间,这与日常路径推荐方法是相吻合的.实验中,取w1=0.8,w2=w3=0.1. 按照传统的经验提取方法,在无OD约束的情况下用相同的权重系数建立经验模型(EM),以及最短路径模型(SP),在实验与讨论部分进行比较分析. 实验使用的GIS软件为MAPGIS K9 SP3和ArcGIS 10.0,数据库软件为SQLServer 2008和Oracle 11 g,软件开发环境为Visual Studio 2010.选择深圳市为研究区,用深圳市2011年11月1号至7号的出租车(共12 448辆)轨迹数据(共7 594万条)对文中提出的模型进行验证,路网为深圳市道路交通图,共101 794条路段.在实验过程中,从深圳市机场、车站、酒店、休闲娱乐地等POI中随机选择组成30对OD,基本覆盖到了深圳市的每个区,如图7所示.实验中首先使用2 km×2 km的约束区,选取5个工作日上午7:00-9:00轨迹数据,对研究区30对OD进行分析. 图7 研究区路网及POIsFig.7 Road network and POIs of study area 首先,选取深圳宝安国际机场—深圳大学作为起止地,图8(a)、8(b)显示的分别是EM与ODCEM两种模型的轨迹,可以看到,在EM中(图8(a))各道路上都有大量的轨迹分布,给定约束OD后(图8中星形符号)很难找到清晰的经验轨迹;在ODCEM中(图8(b))约束OD之间的轨迹较为清晰,而其他道路上的轨迹则非常少. 接着,计算两种模型下的路段经验,结果表明,在EM中,路段经验分散(范围为0~13 668,标准差SD=163.2),道路等级高或路网密度大的区域路段经验值高,例如商业区和主干道,而在ODCEM中,路段经验比较集中(范围为0~392,标准差SD=4.6),OD范围外的路段经验大多为0,OD范围内的路段经验也比EM中低得多.任意选择A、B两个区域内的70条路段(A位于OD范围内,B位于OD范围外,如图8(b)所示,其中,区域A包含392条路段,区域B包含299条路段),分别统计ODCEM和EM下的路段经验,其结果如图9(a)、9(b)所示.可以看出,EM在区域A和B中均有很高的路段经验,而ODCEM的路段经验在区域B几乎全部为0.这是因为区域B内的路段与本次出行无关,该区域的路段上没有ODC-T,而EM由于没有限制约束条件,因此依然存在很高的路段经验. 图8 EM与ODCEM的轨迹Fig.8 Trajectories of EM and ODCEM 图9 ODCEM与EM的路段经验Fig.9 Road experience of ODCEM and EM 最后,将道路的行政等级图(10(a))与EM、ODCEM的路段经验等级图(10(b)、10(c))进行对比,发现EM的经验等级与该区域的道路等级更为相似.进一步将两种模型的路段经验与道路等级进行相关性分析,结果为:EM的经验值与道路等级的相关性系数为0.393,即在0.01水平上显著相关,而ODCEM的经验值与道路行政等级相关性系数仅为0.065. 图10 道路、EM、ODCEM等级图Fig.10 Levels of road,EM and ODCEM 分别用EM和ODCEM进行路径规划,生成的路径如图11(a)和图11(b)所示.对比图10(b)和图11(a)可以看出,EM模型将路线规划在总的路段经验较高的路段上,而图10(c)和图11(b)则显示ODCEM将路径规划在ODC-SE较高的路段上.对比图11(a)和图11(b)还可以发现,EM的路径比较绕远,大大超出OD范围(这主要是因为出行OD范围外的路段也有较高的经验值),而ODCEM的路径则与其约束下的轨迹、约束下的道路等级相吻合. 图11 EM和ODCEM路径Fig.11 Routes of EM and ODCEM 接下来分别用EM、ODCEM及SP3种模型对30对OD进行路径规划,任选其中4对的结果如图12所示,可以看出,SP路径距离最短,EM路径比较绕远,ODCEM路径长度居中. 图12 任意4对OD的3种模型路径图Fig.12 Routes of 3 models for 4 random OD pairs 为了验证3种模型规划的路径上经验的高低,利用ODC-Trajectory计算每条路径单位距离的轨迹点的数量,称之为轨迹覆盖度: (10) 式中,numroutei表示路径i上的经验轨迹点的数量,Lengthroutei表示路径i的长度. 分别计算统计30对OD在不同路径上的轨迹覆盖度、路径长度、通行时间和平均通行速度,结果如图13(a)至13(d)所示.总体来看,ODCEM的轨迹覆盖度最高,通行时间最短,通行速度最快,通行距离位于EM和SP之间. 图13 30对OD的轨迹覆盖度,通行长度,通行时间和通行速度 统计结果(见表1)也显示:83.3%以上的ODCEM轨迹覆盖度大于SP和EM,即ODCEM是实际出租车轨迹最多的路径;在路径长度上,ODCEM中86.7%比EM短,但都长于SP;在通行时间上,93.3%以上的ODCEM都比EM及SP节省时间;在通行速度上,ODCEM中有76.7%比EM快,且全部优于SP. 表1 30对OD的ODCEM优秀率Table 1 Excellence rate of ODCEM in 30 pairs of OD 这说明,在通行距离上,SP无可比拟,但本研究中提出的ODCEM在充分拟合司机经验的基础上,运行时间和通行速度都比较优秀.从速度上看,也存在个别EM速度较高的情况,主要是因为这些路径处于路况较好的外环道路上,是以更多的时间和更长的距离换取的高速度,这不符合出租车出行的规律(出租车出行会更多地考虑出行的距离),实际上增大了出行成本.因此,文中提出的ODCEM在充分考虑出租车司机经验的基础上兼顾到了出行的时间、距离及速度,是一种行之有效的经验提取模型. 根据格网划分的原则,约束点格网的大小要适中,过大会影响结果的精度,过小则在数据存储和运算上效率不高.实验中分别以1 km×1 km、2 km×2 km、4 km×4 km、6 km×6 km的格网大小进行讨论.在4种情况下,30对OD的ODCEM路径的总长度、总时间统计结果如图14所示. 由图14可以看出:路径总长度及通行总时间都随着格网的增大而增大,说明随着约束尺度的增加,模型的准确性有所下降,导致路径长度和时间的增加.这说明,约束尺度应该越小越好,但是如果约束尺度过小,精确约束下的子轨迹数也必将减少.为了进一步验证不同约束尺度下子轨迹数目的变化,实验中增加了OD对的个数(随机选择50个POI,产生50×50=2 500个OD对),程序运行时间及子轨迹为0的OD对所占的百分比如图15所示.可以看出,约束尺度为1 km×1 km时33%的OD对之间子轨迹为0,随着约束尺度的增加,在2 km×2 km时迅速下降到13%,之后继续下降直到6 km×6 km时的3.5%,如果约束尺度继续增加,直到整个研究区为一个网格,即无约束的经验模型,此时不存在子轨迹为0的OD对.因此,约束尺度过小,会导致精确约束下的子轨迹为0,也无法获取有效的经验.另外,程序运行时间随着约束尺度的增加而增加. 图14 4种格网下30对OD的ODCEM总距离和总时间Fig.14 Total travel distance and travel time of ODCEM of 30 OD pairs under four different grid sizes 图15 4种格网下轨迹为0的OD对百分比及程序运行时间Fig.15 Percentage of OD pairs with no trip and its program running time under four different grid sizes 综合以上分析,在本研究背景下,2 km×2 km的约束点大小比较合适,在此约束尺度下,经验轨迹比较精确,数目适中,且程序运行效率在可接受的范围内. 文中提出OD约束的概念,建立相应的OD约束经验模型,以模拟司机的出行路线,在路径规划时兼顾出行的时间、距离及速度等因素,是一种行之有效的经验提取方法.在实验中发现,研究区的约束大小为2 km×2 km时较为合理. 但是,实验过程中对时间尺度的划分比较粗略,也没能处理跨越两个时间段的轨迹,因此损失了部分轨迹信息;另外,如果能够对经验数据库进行实时更新,结果将会更加准确,这将是下一步研究的方向. [1] 袁晶.大规模轨迹数据的检索,挖掘及应用 [D].合肥:中国科学技术大学,2012. [2] SONG C,QU Z,BLUMN N,et al.Limits of predictability in human mobility [J].Science,2010,327(5968):1018-1021. [3] GONG J F,YU Z,CHEN N N.An analysis of drivers’ route choice behavior in urban road networks based on GPS data [C]∥The First International Conference of Transportation Engineering.Chengdu:[s.n.],2007:515-520. [4] YUAN J,ZHENG Y,ZHANG XIE W,et al. T-drive:driving directions based on taxi trajectories[OL/EB].[2011-12-31].http:∥www.docin.com/p-338527489.html. [5] 唐炉亮,常晓猛,李清泉,等.基于蚁群优化算法与出租车GPS数据的公众出行路径优化 [J].中国公路学报,2011,24(2):89-95. TANG Lu-lianng,CHANG Xiao-meng,LI Qing-quan,et al.Public travel route optimization based on ant colony optimization algorithm and taxi GPS data [J].China Journal of Highway and Transport,2011,24(2):89-95. [6] LI Q Q,ZENG Z,ZHANG T,et al.Path-finding through flexible hierarchical road networks-An experiential approach using taxi trajectory data [J].International Journal of Applied Eearth Observation and Geoinformation,2011(13):110-119. [7] 胡继华,黄泽,邓俊,等.融合出租车驾驶经验的层次路径规划方法 [J].交通运输系统工程与信息,2013,13(1):185-192. HU Ji-hua,HUANG Zhe,DENG Jun,et al.Hierarchical path planning method based on taxi driver experiences [J].Journal of Transportation Systems Engineering and Information Technology,2013,13(1):185-192. [8] WEI L Y,ZHENG Y,PENG W C.Constructing popular routes from uncertain trajectories [C]∥18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Beijing:[s.n.],2012:195-203. [9] 唐炉亮,常晓猛,李清泉.出租车经验知识建模与路径规划算法 [J].测绘学报.2010,39(4):404-409. TANG Lu-liang,CHANG Xiao-meng,LI Qing-quan.The knowledge modeling and route planning based on taxi’ experience [J].ActaGeodaetica et Cartographica Sinica,2010,39(4):404-409. [10] 曾喆.面向导航路径选择的道路网络经验层级模型研究 [D].武汉:武汉大学,2010. [11] JIANG B.Street hierarchies:a minority of streets account for a majority of traffic flow [J].International Journnal of Geographical Informational Science,2009,23(8):1033-1048. [12] 吴健生,黄力,刘瑜,等.基于手机基站数据的城市交通流量模拟 [J].地理学报,2012,67(12):1657-1665. WU Jian-sheng,HUANG Li,LIU Yu,et al.Traffic flow simulation based on call detail records [J].Acta Geographica Sinica,2012,67(12):1657-1665. [13] 辛飞飞,陈小鸿,林航飞.浮动车数据路网时空分布特征研究 [J].中国公路学报,2008,21(4):105-110. XIN Fei-fei,CHEN Xiao-hong,LIN Hang-fei.Research on time space distribution characteristics of floating car data in road network [J].China Journal of Highway and Transport,2008,21(4):105-110. [14] 姜桂艳,常安德,李琦,等.基于出租车GPS数据的路段平均速度估计模型 [J].西南交通大学学报,2011,46(4):638-644. JIANG Gui-yan,CHANG An-de,LI Qi,et al.Estimation models for average speed of traffic flowbased on GPS data of taxi [J].Journal of Southwest Jiaotong University,2011,46(4):638-644. [15] 朱广宇,杜崇,张彭.基于基线漂移校正的旅行时间预测模型 [J].华南理工大学学报(自然科学报),2016,44(8):131-138. ZHU Guang-yu,DU Cong,ZHANG Peng.A travel time forecasting model based on baseline drift correction [J].Journal of South China University of Technology(Natural Science Edition),2016,44(8):131-138. [16] CHERKASSKY B V,GOLDBERG A V,RADZIK T.Shortest paths algorithms:theory and experimental eva-luation [J].Mathematical Programming,1996,73(2):129-174. s:Supported by the National Natural Science Foundation of China(41371422,41201385,41301426,41301427) OriginDestinationConstraintExperienceModelofTaxiandPathPlanning PANXiao-fang1,2ZHOUShun-ping1YANGLin1WANBo1 (1.Faculty of Information Engineering,China University of Geosciences (Wuhan),Wuhan 430074,Hubei,China;2.School of Geographic Sciences,Xinyang Normal University,Xinyang 464000,Henan,China) Extracting the driver’s experience from taxi trajectories to guide the public travel is an important application of trajectory data.In order to avoid the inaccurate results caused by ignoring the origin and destination in the experience extracting process of traditional methods,this paper proposes an origin destination constraint experience model (ODCEM).Then,the traditional experience model,the ODCEM and the shortest path model are compared by the experiments in Shenzhen city.The results shows that (1) the ODCEM can successfully simulate the taxi driver’s travel experience during the experience extracting and the path planning;(2) in comparison with the other two methods,the ODCEM increases the travel time and the speed respectively by more than 93.3% and more than 76.7%;and (3) the travel distance of the ODCEM is between those recommended by the other two methods.Finally,the influence of the constraint scale is discussed.It is found that the desirable constraint size is 2 km×2 km. origin destination constraint;taxi trajectory;experience model;path planning 2016-09-12 国家自然科学基金资助项目(41371422,41201385,41301426,41301427) 潘晓芳(1979-),女,博士,讲师,主要从事空间数据库、GIS-T研究.E-mail:xfpanem@163.com †通信作者:周顺平(1967-),男,教授,博士生导师,主要从事空间数据库挖掘和地理信息系统软件工程研究.E-mail:zhoushunping@mapgis.com 1000-565X(2017)08-0057-08 U 491 10.3969/j.issn.1000-565X.2017.08.009
2 ODCEM的建立
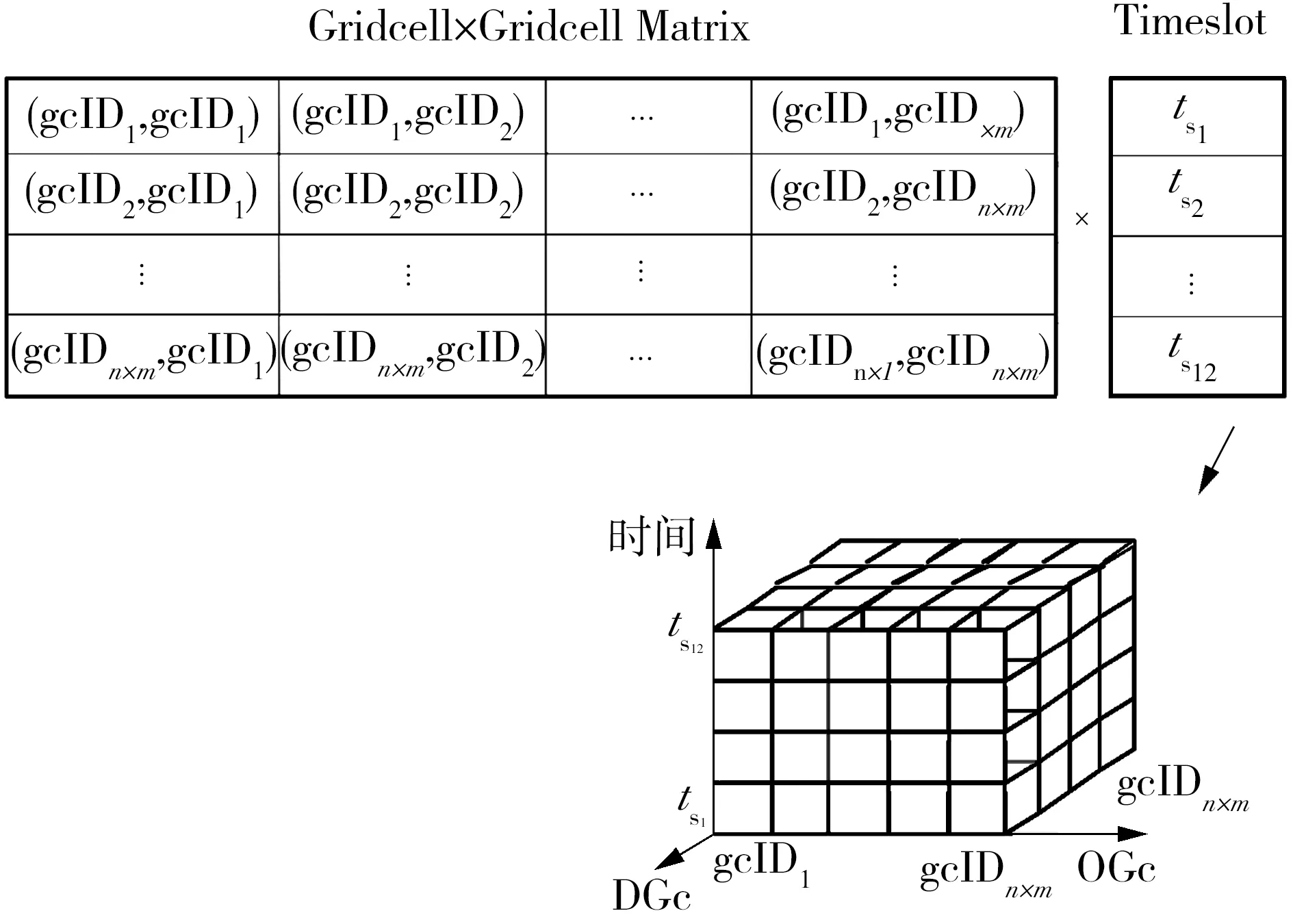
2.1 建模方法
2.2 OD约束的路段经验系数
3 实验与讨论
3.1 实验环境
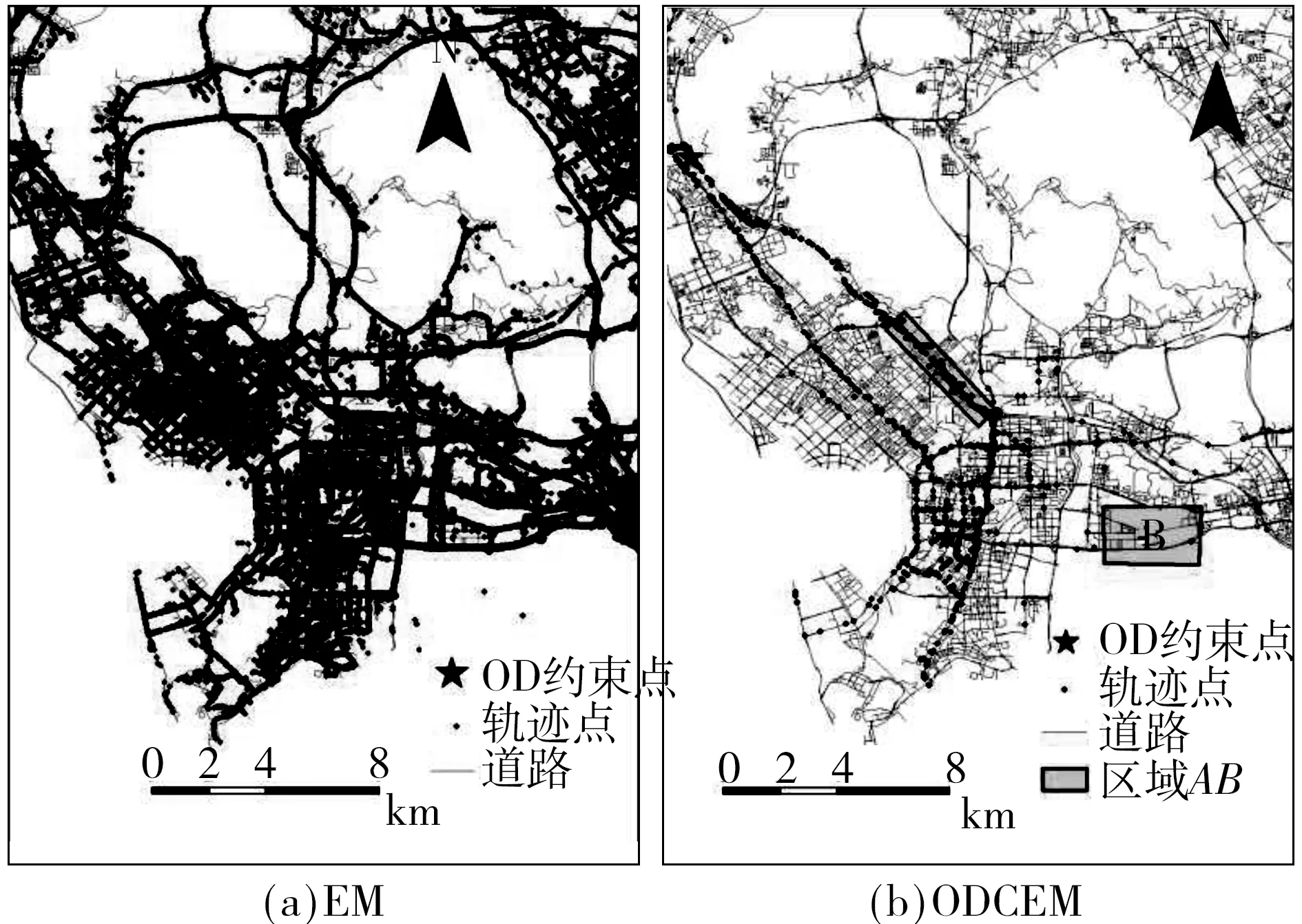
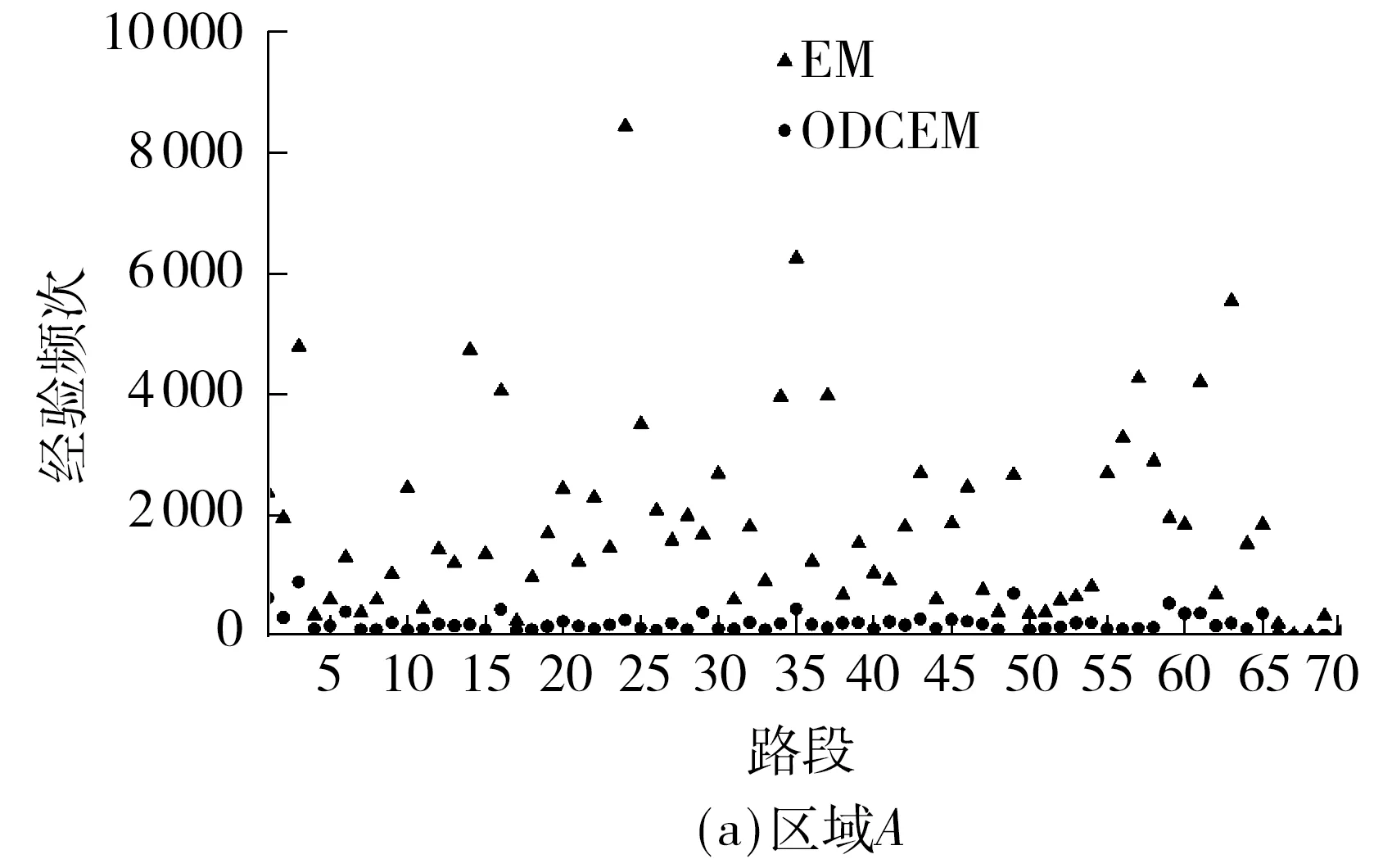
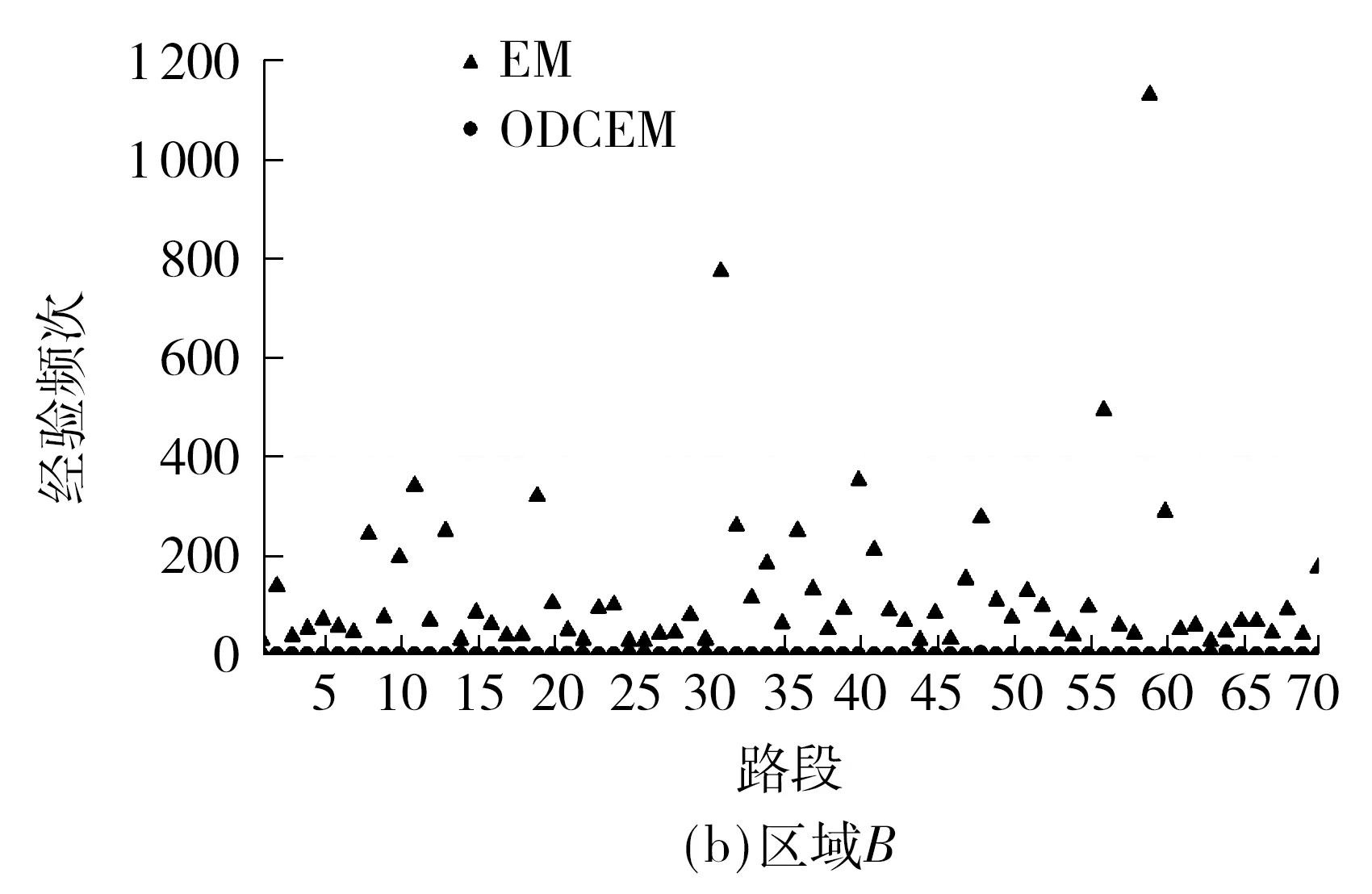
3.2 OD约束下的轨迹与路段经验
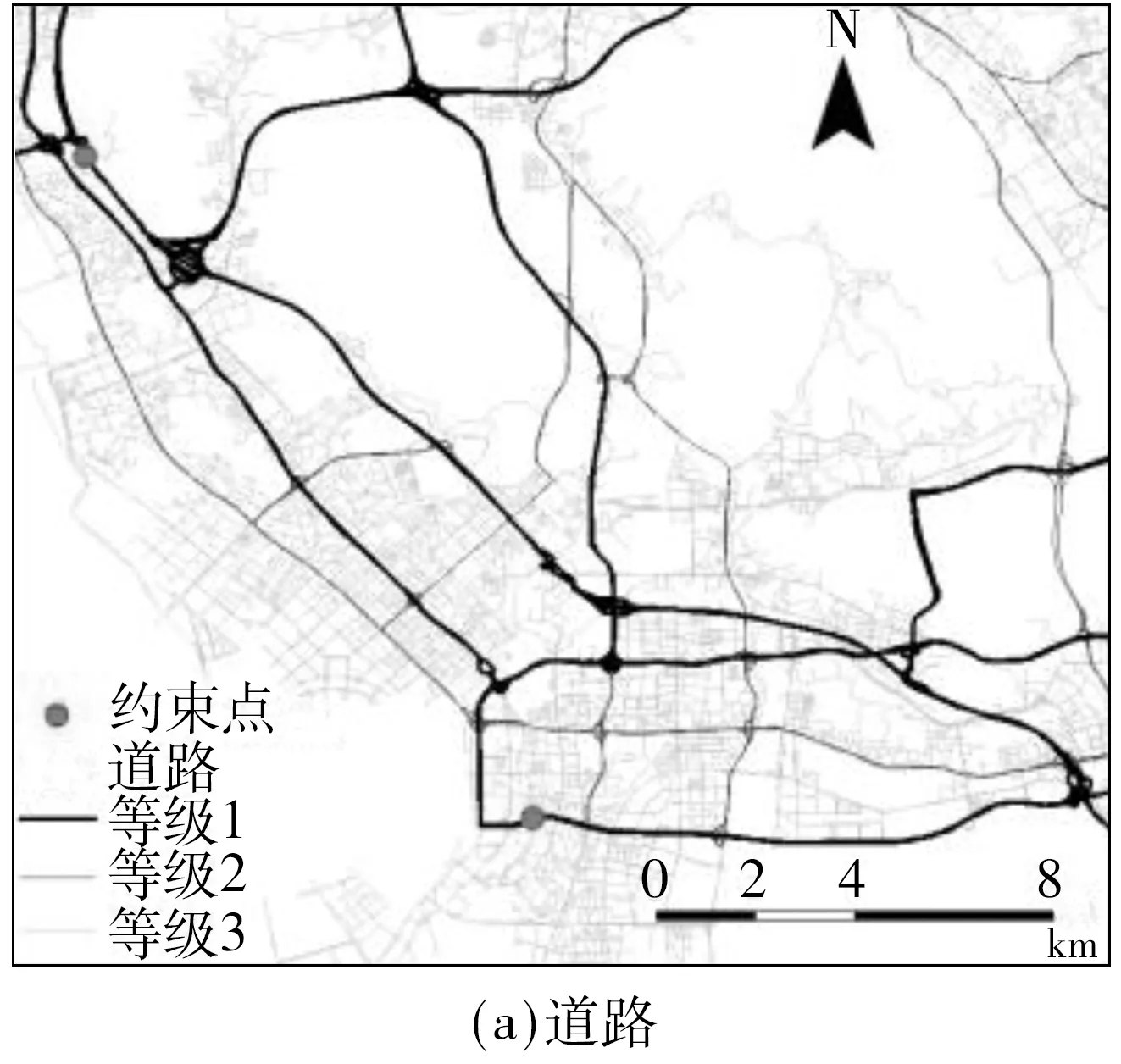
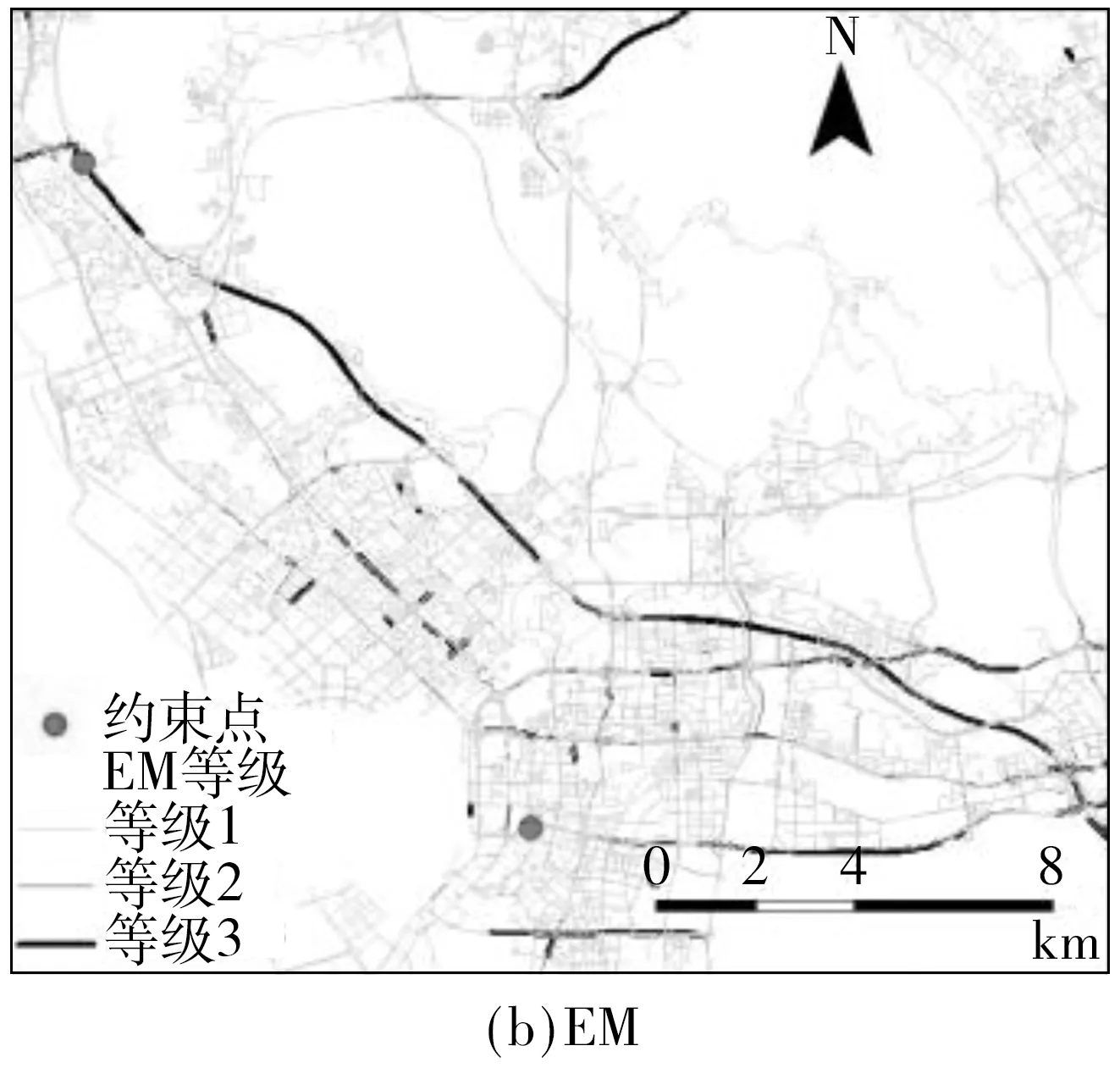
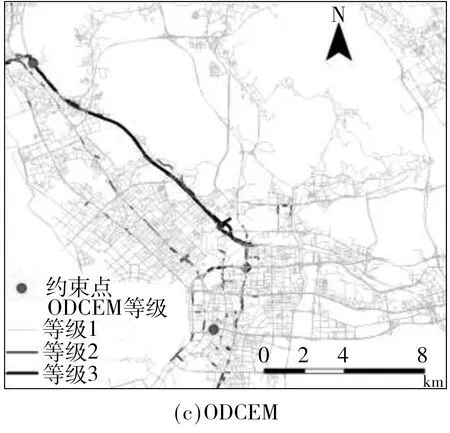
3.3 OD约束下的经验路径
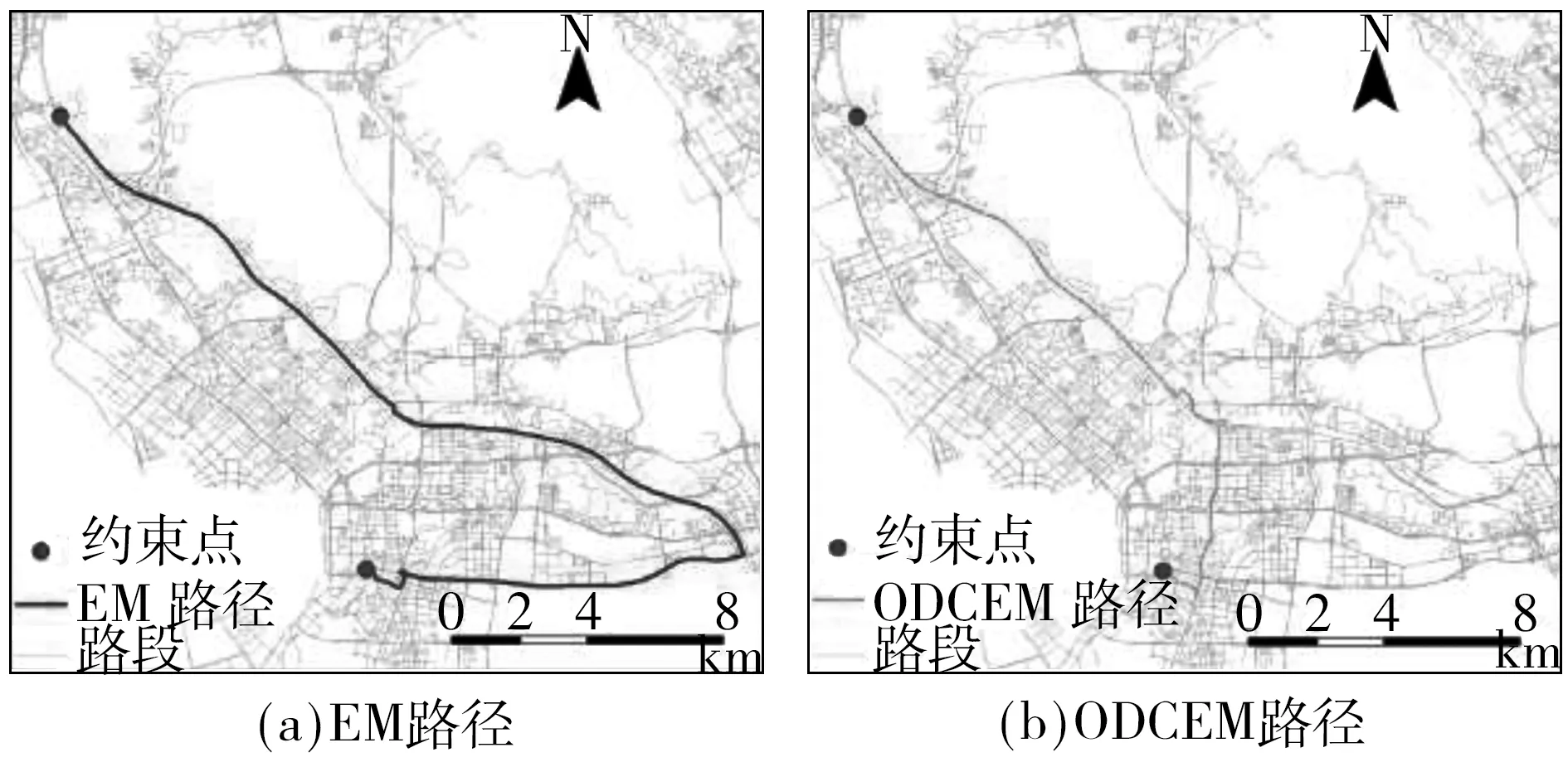
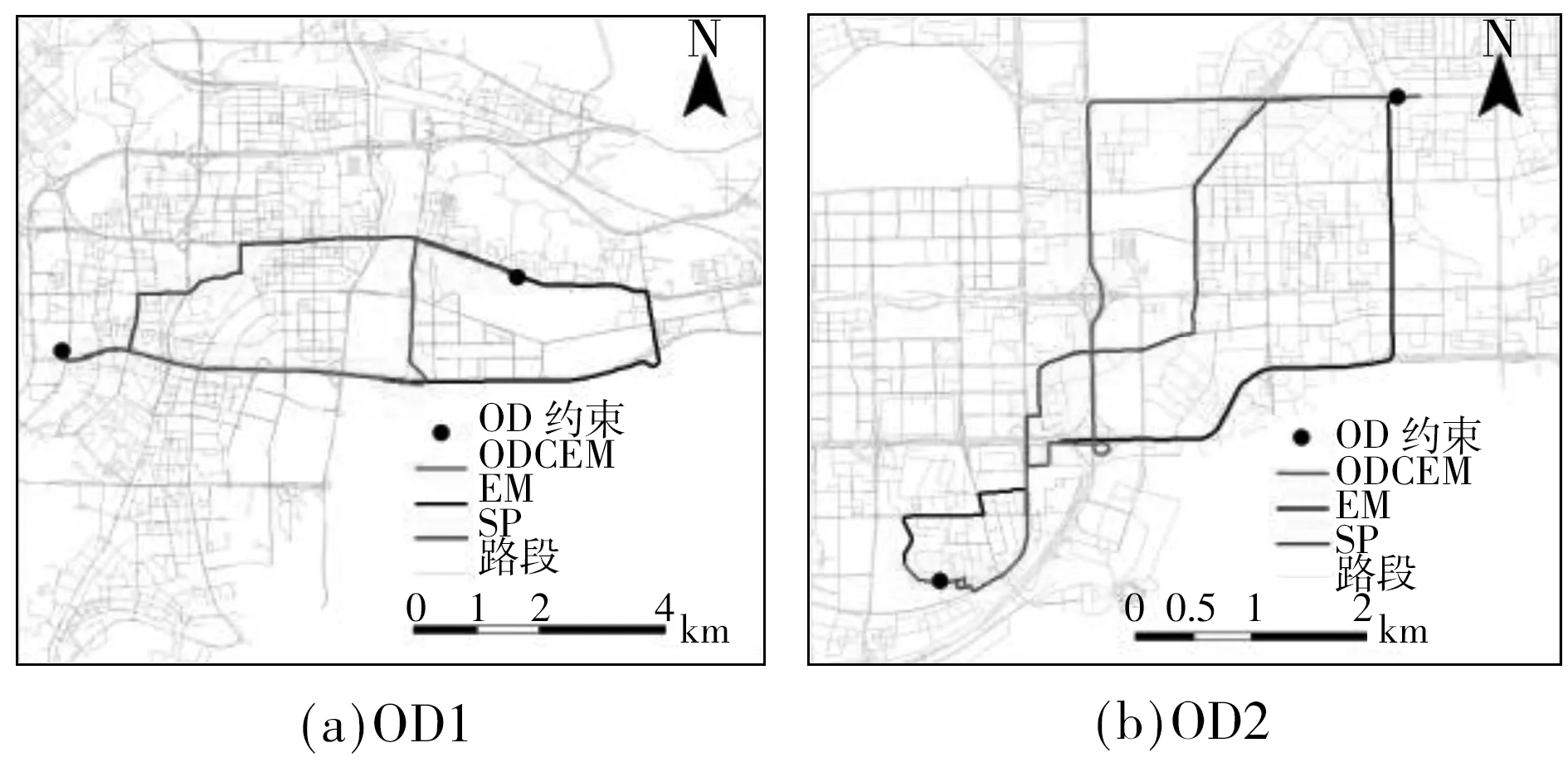

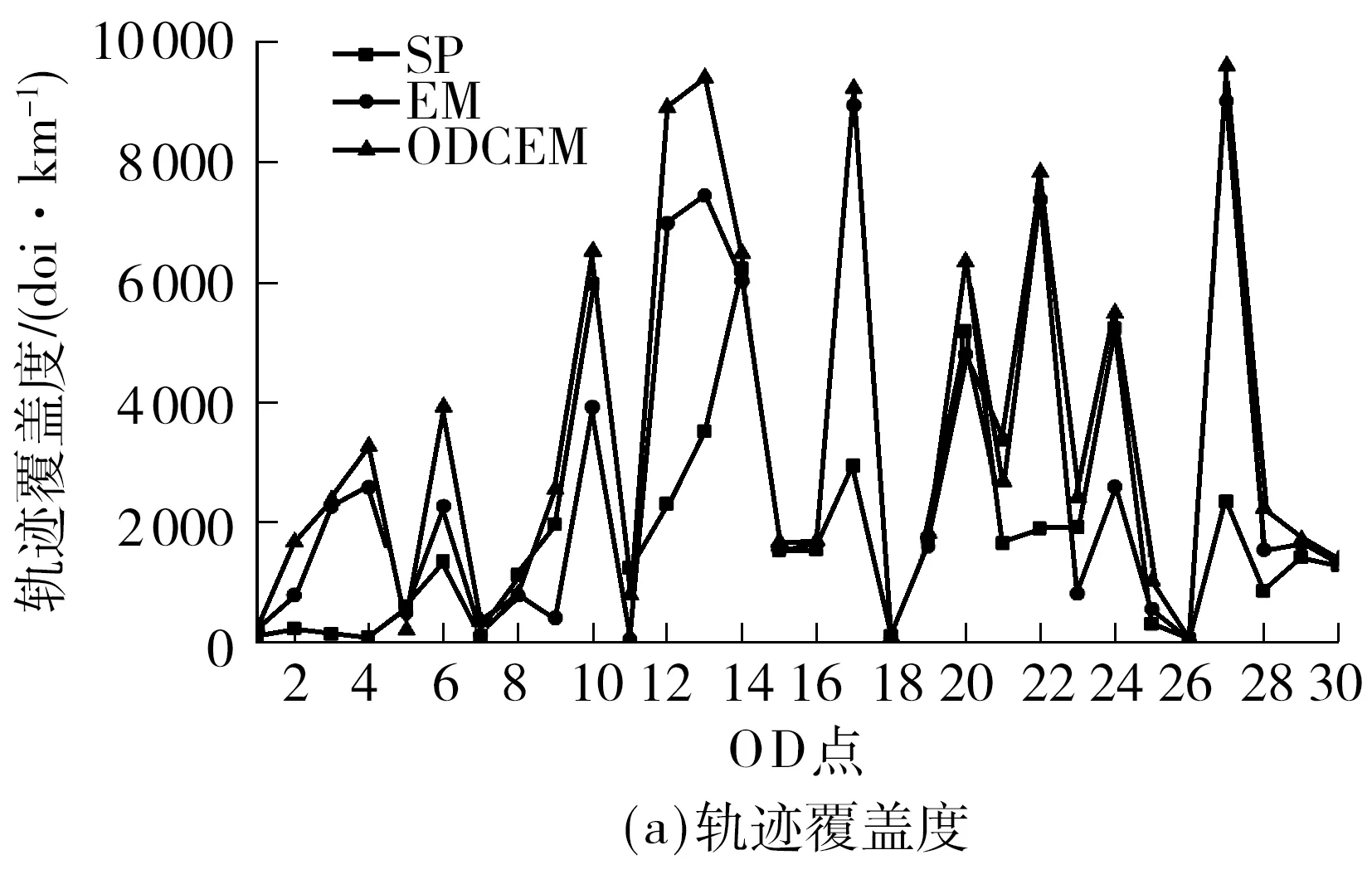
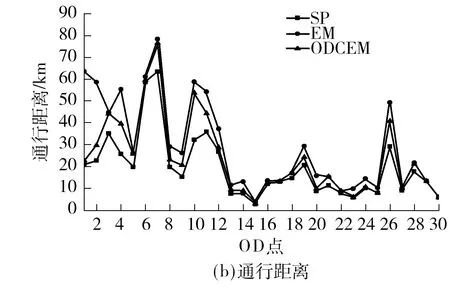

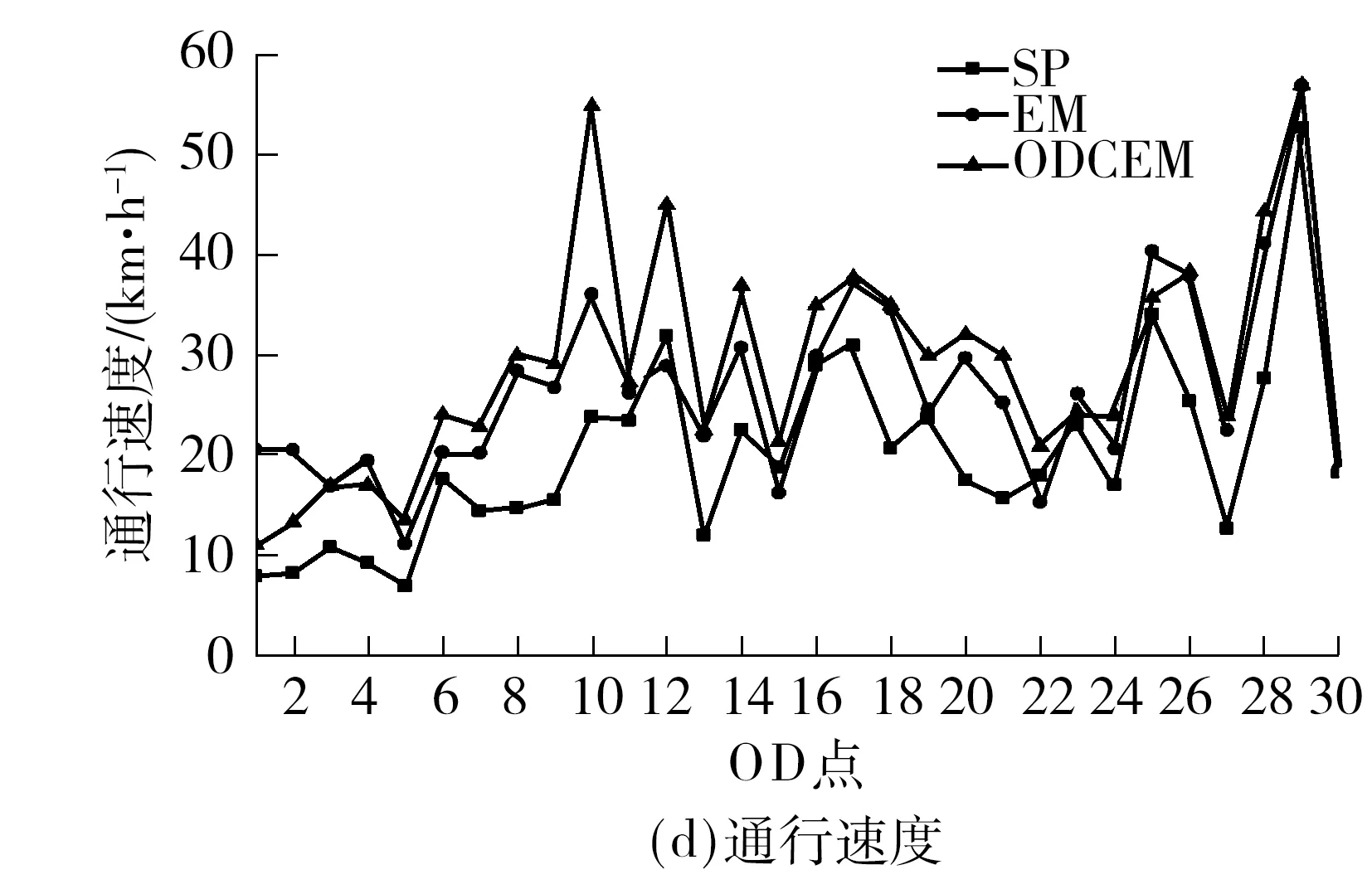
Fig.13 Trajectory coverage,travel distance,travel time and travel speed of 30 OD pairs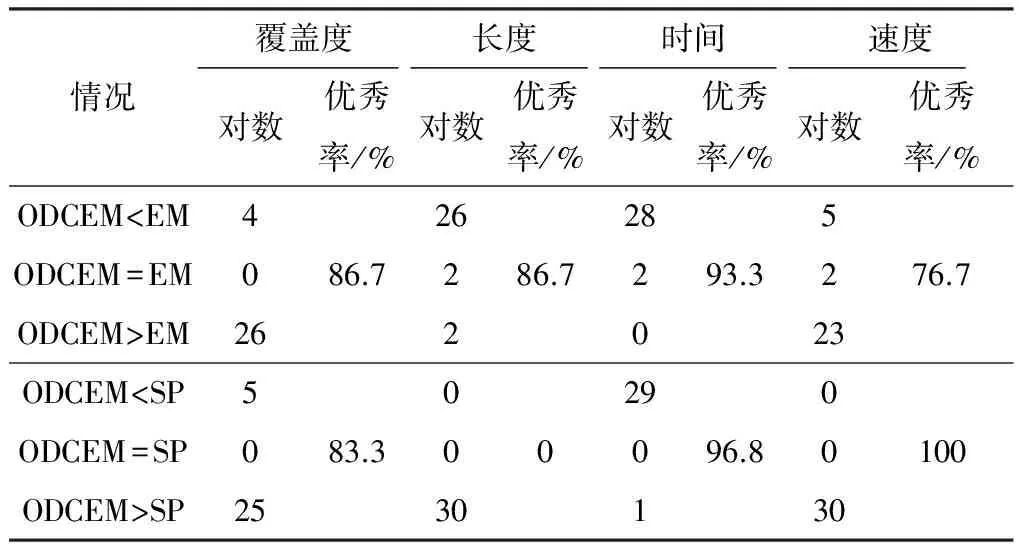
3.4 约束尺度分析

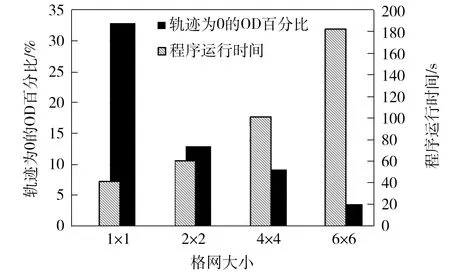
4 结语

