小题不必大作，换种思路柳暗花明

蒋士绚

1904年，美国圣路易斯举办了第三届奥林匹克运动会.在进行撑竿跳高比赛时，发生了一段意外.

日本运动员佐间代富士在试跳时，从容不迫地走进沙坑，把手中的撑竿用力插到沙土里，另一端搭在高处的横梁上.固定好后，他顺着竿子往上爬，一直爬到最高处，然后越过横梁后，从另一边顺着竹竿滑下来.所有人看得目瞪口呆：怎么会有这样的撑竿比赛方法？全场嘘声一片.裁判们十分犯难.因为按照比赛规则，日本选手并没有违规，只不过他投机取巧了而已.经过裁判组的讨论，还是取消了他的成绩.

日本选手据理力争，认为自己并没有违反规则，他可以这样做.于是裁判补充了撑竿比赛的规则，要求运动员必须先有一段助跑过程.

日本选手在第二次试跳时，有了助跑动作.但跑到沙坑附近，他又抓住撑竿，顺着竿子往上爬.这一次他又取得了好成绩，这让裁判很为难，不得不承认他又钻了规则的漏洞.于是，裁判组再次召开紧急会议，确定了撑竿比赛要有助跑，并且不能交替使用双手的动作.这项规则确定下来之后，一直沿用到现在.

这则近乎笑话的轶闻让人感到那位日本选手的精明和狡猾.如果每位选手都像他那样投机取巧，岂不天下大乱？但如果换一种角度去看，就会发现，在我们考试的时候，由于填空题和选择题只要求给出最终的结果，不需要写出解题的思路和过程，因此我们可借鉴这位日本选手的思路，只需要在遵守“规则”的前提下，采用一系列“投机取巧”的办法得到题目的最终结果，这样能够有效节约答题时间，提高解题效率.

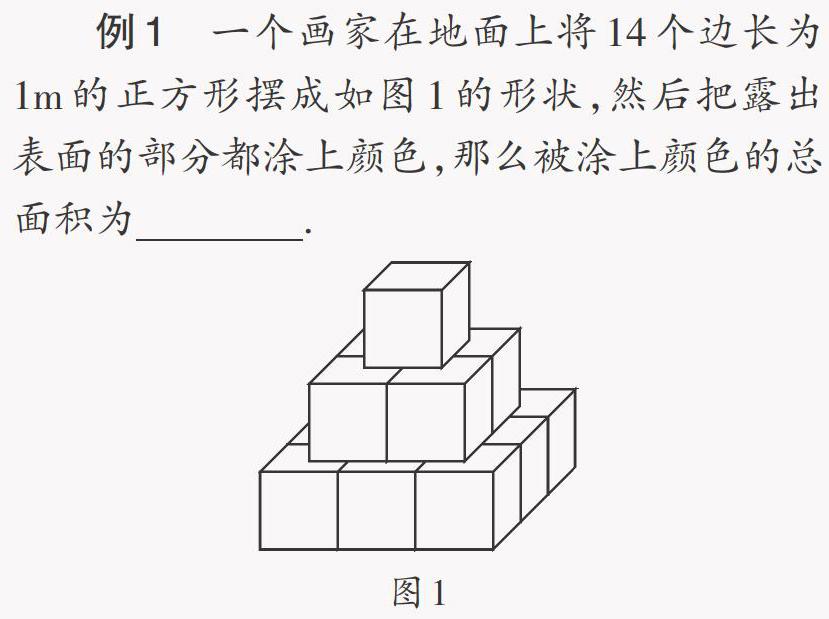
例1 一个画家在地面上将14个边长为1m的正方形摆成如图1的形状，然后把露出表面的部分都涂上颜色，那么被涂上颜色的总面积为 .

【思路分析】这个几何体的表面积从几何体的方向看可分为五部分，从上往下看，看到的是一个边长为3的正方形，从前后左右看，看到的都是6个小正方形.因此这个几何体的总面积和为33m2.

【点评】在解决这个问题的过程中，不管这个几何体是如何不规则，但用从不同方向看的方法，可以将这个几何体的表面积转化为5个规则的平面图形.

例2 如图2，从棱长为10的正方体的一顶点处挖去一个棱长为1的小正方体，则剩下图形的表面积为（ ）.

A.600 B.599 C.598 D.597

【思路分析】这个缺角的立方体的表面面向的方向无非是向上、向下、向左、向右、向前、向后六个方向，从六个方向看立方体，得到的都是边长为10的正方形，所以该立方体的表面积是600.

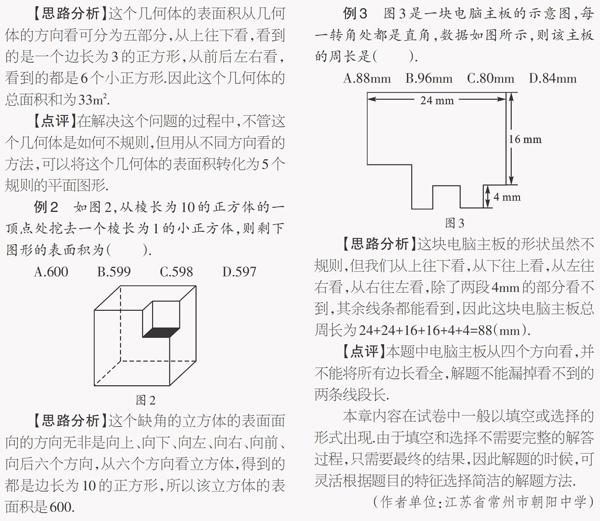
例3 图3是一块电脑主板的示意图，每一转角处都是直角，数据如图所示，则该主板的周长是（ ）.

A.88mm B.96mm C.80mm D.84mm

【思路分析】这块电脑主板的形状虽然不规则，但我们从上往下看，从下往上看，从左往右看，从右往左看，除了两段4mm的部分看不到，其余线条都能看到，因此这块电脑主板总周长为24+24+16+16+4+4=88（mm）.

【點评】本题中电脑主板从四个方向看，并不能将所有边长看全，解题不能漏掉看不到的两条线段长.

本章内容在试卷中一般以填空或选择的形式出现.由于填空和选择不需要完整的解答过程，只需要最终的结果，因此解题的时候，可灵活根据题目的特征选择简洁的解题方法.

（作者单位：江苏省常州市朝阳中学）