用于多比特正交发射机的基于图形转换的全自动预失真技术
沈逸磊,薛 盼,叶 峰,洪志良
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
用于多比特正交发射机的基于图形转换的全自动预失真技术
沈逸磊,薛 盼,叶 峰,洪志良
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
多比特正交架构是全数字发射机方案中最有前景的一种,但因为存在着显著的非线性,而需要复杂的二维预失真,并且前人提出的迭代测量法建立预失真表时间长约1ms.本文提出了图样转换的方案来解决预失真表建立时间过长的问题.本文方案将预失真表的建立时间缩短到20μs之内,同时对7.2dB PAPR和40MHz带宽的长期演进(Long Term Evolation, LTE)信号,布局前仿真中预失真后信号带内误差能减少到-30.07dB.本文方案不仅节省了预失真过程的时间和功耗,也使多比特正交发射机预失真表的实时建立首次成为可能.
全数字发射机; 多比特正交功放; 二维预失真; 图样转换
近年来无线通信产业和市场发展迅速.采用线性功率放大器(简称功放)的传统模拟架构继续占据着设计和市场的主流,新型的全数字架构的发射机正在越来越受到研究者和工业界的关注,这其中有一部分应当归功于全数字架构发射机良好的灵活性和可移植性.此外,全数字架构发射机可以应用开关功放也是采用全数字架构的一个重要的因素,因为开关功放具有能量效率高的优势.
为了利用好全数字架构发射机的优势,前人曾提出过许多方案.根据功放输入端的比特数,这些架构可以分为多比特架构和单比特架构两大类.在每一类中,又可以按照传统的正交、极化、移相的框架进行分类.移相单比特架构如文献[1],巧妙地将典型的移相调制以脉宽调制移植到单比特架构中.但是,这类设计中的单比特功放不可避免地会引入较多的带外噪声,这就需要片上或片外的滤波网络对其进一步滤除.此外,这种方案只对峰均功率比(Peak-to-Average Power Ratio, PAPR)不太大的信号效果较好.文献[2]中提出的单比特极化调制,在对大动态范围的适应性和误差向量幅度(Error Vector Magnitude, EVM)上表现得比单比特移相方案更好,但带外噪声的问题仍然没有解决.此外,这两种方案都需要复杂的CORDIC计算.文献[3]中的单比特正交架构采用的是ΔΣ调制,虽然不需CORDIC计算,但ΔΣ调制带来的带外噪声比前两种方案都更高.因此,带外噪声压倒性地占据了功耗的主要部分,功放能量效率变低,而这与采用全数字架构希望能获得更高能量效率的初衷背道而驰,这就使单比特正交架构的方案的实用性受到了挑战.
因为单比特架构的发射机一直受带外噪声的问题困扰,在全数字发射机的框架下,多比特架构是不言自明的另一个选择.但代价是多比特发射机存在单比特架构天生免疫的非线性问题.文献[4]展示了一种多比特极化方案,其中采用的是线性功放常用的预失真技术——将预失真分解为AM-AM和AM-PM两部分分别进行,预失真后信号能达到-28dB的EVM和19.8%的系统效率.尽管该设计的性能令人满意,但一般认为极化调制发射机一般而言对宽带信号的支持较差[5],这很大程度上阻碍了其在当今无线通信场景中的广泛应用.
排除了其他的可能性之后,最有前景的全数字发射机架构就是正交架构.因此,本文以下的讨论将围绕全数字多比特正交架构展开.但在多比特正交架构的领域中目前还没有很大的进展,这中间很大一部分要归咎于该架构中独有的极其复杂的非线性特性.线性功放中的非线性只有AM-AM和AM-PM成分,即只有幅度是非线性的自变量,因而根据定义,这种非线性是一维的.相反,多比特正交架构中的非线性中还存在PM-PM和PM-AM成分,并且相当显著,因而幅度和相位的相互作用决定了多比特正交架构中非线性的二维特性.因为先前发表的预失真技术方案多数是针对只有一维非线性的线性功放的,像文献[4]那样简单地模仿用在线性功放上的预失真技术,在多比特正交架构中将不会再奏效.为了实现多比特正交方案,我们需要的是一种针对二维非线性的预失真技术.
文献[6]中所展示的预失真方案是我们所知的最有前景的方案,也是多比特正交架构中少有的经过了硬件验证的一个设计.该方案中,预失真器的实现借助的是基于查找表的双线性插值,在这以外还内建有一条完整的自测量通路和数字信号处理单元来生成预失真器查表插值所需的表项.这个系统有两种工作模式: 训练模式和发射模式.在训练模式下,系统发射一个训练序列,同时根据反馈通路上测得的功放输出值,迭代地校正功放的输入以使其接近理想的经过预失真的值.待所有预失真的映射都已经得到并储存,系统可进入发射模式,并通过查找相应的预失真数据以及插值对输入进行预失真.查找表和插值的结合大大降低了需要存储的数据规模,并且让方案变得切实可行,还能保证预失真性能良好.这种基于查找表的双线性插值,对40MHz带宽信号,在17.1dBm输出功率条件下得到了-28dB的EVM,这个结果是比较令人满意的.
虽然已经有了很大的进步,这个解决方案还不能说是十全十美的.遗留的问题有两点: 第一,该方案的迭代特点导致预失真查找表的建立相当低效,根据文中描述需要近1ms;第二,迭代方案的收敛特性在文中没有提及,而该方案是否对比较一般的多比特正交方案都适用是有疑问的.为了解决这些问题,我们提出了一种新的基于非迭代的图样转换的预失真查找表建立方案,优化后的方案可以避免上文的提到的两个缺陷.
本文的结构如下.第2节呈现的是图样转换的预失真查找表建立方案.第3节详细介绍图样转换的原理和实现.第4节给出综合和仿真结果.
1 系统描述
在深入介绍之前,有必要大致介绍一下功放的失真特性和预失真技术.图样指的是结构化的信号矢量的序列.图1绘出了两对图样PRED和SQpred、SQdist和DIST之间的关系,这些图样反映了功放的输入-输出映射.模拟输出图样SQpred是方格,而其对应的未失真的数字输入图样是PRED.数字输入图样SQdist是方格,而其对应的失真的模拟输出图样是DIST.
1.1 系统概要
发射机有两个工作模式: 建立模式和发射模式.为了能让发射机发射不失真的信号,预失真器在发射模式下开启,其查找表即PRED存储在存储器中.为此,系统首先要被配置在建立模式下以建立预失真器所需的预失真表PRED.图2是当前方案的示意图.
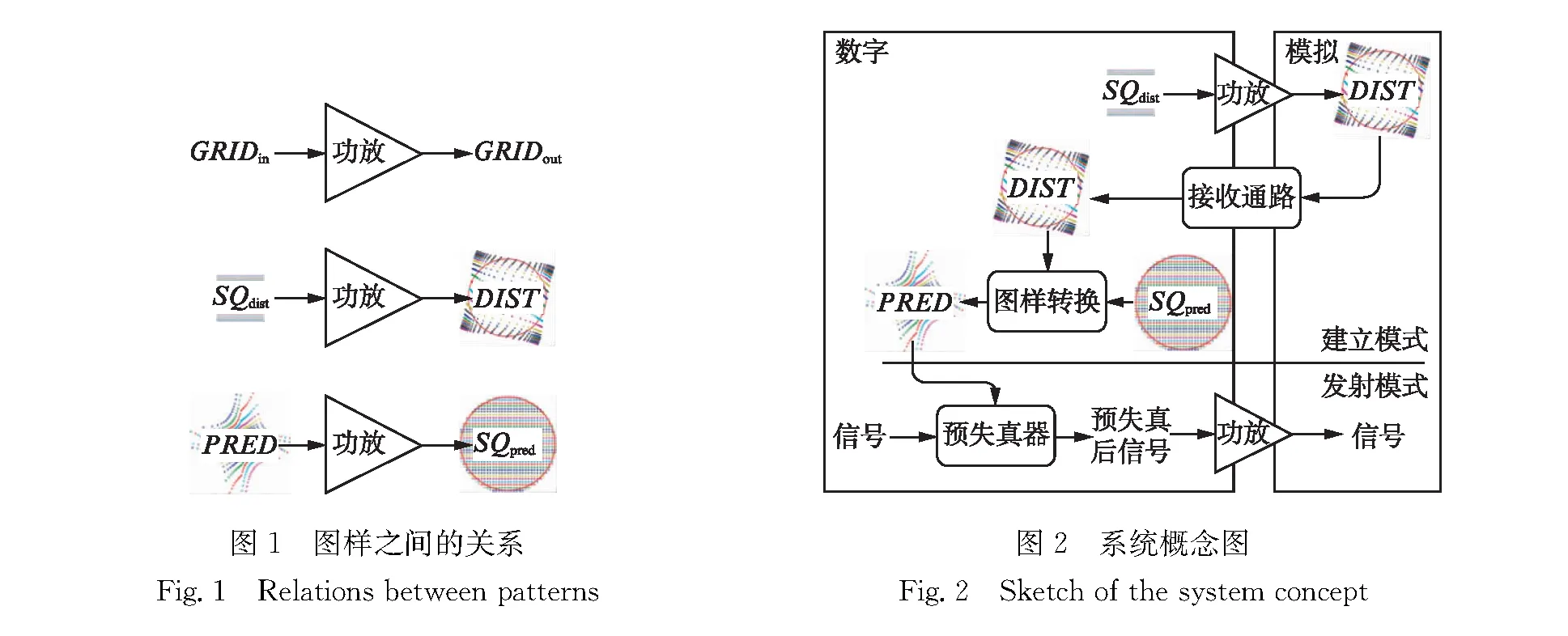
建立模式的流程大致如下.首先,功放输入一个扫遍SQdist的扫描信号,而接收通路测量失真的功放输出以建立DIST.之后图样转换器开始工作,根据给定的SQpred根据DIST逐点将SQpred转换为PRED并将PRED写入存储器中,以待发射模式下由预失真器访问.
1.2 系统的实现
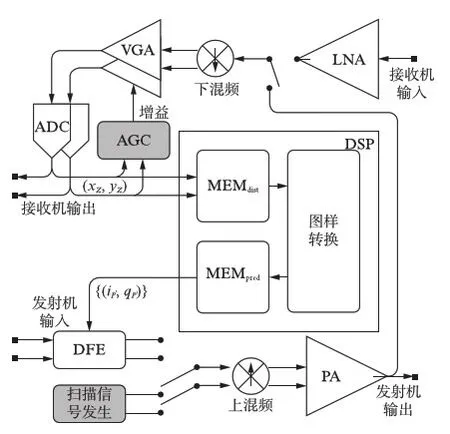
图3 系统模块图Fig.3 Block diagram of the system
本设计系统框图见图3.整个系统主体由发射机、接收机和定制的数字信号处理单元(Digital Signal Processing, DSP)构成,在系统级上形成一个环.发射机由数字前端(Digital Front End, DFE)、数字上混频器、功放(Power Amplifier, PA)组成,其中DFE包含升采样滤波器和数字预失真器两部分.接收机由低噪声放大器(Low Noise Amplifier, LNA)、数字下混频器、可变增益放大器(Variable Gain Amplifer, VGA)、数模转换器(Analog-to-Digital Converter, ADC)级联而成.自动增益控制器(Automatic Gain Controller, AGC)控制VGA的增益,扫描信号发生器输出可馈给上混频器,两模块其实都是图3中未绘出的系统控制器的一部分.DSP从ADC获得信号,继而将预失真表送给预失真器.DSP由三部分构成: MEMdist用于存储失真图样DIST,MEMpred用于存储预失真图样PRED,图样转换器实现构造PRED的运算.图样转换的详细算法和过程在下一节详述.
系统模式可以用串行外围接口(Serial Peripheral Interface, SPI)等进行配置.在建立模式下,上混频器选择扫描信号为输入,接收机作为接收通路来测量功放输出;功放输出衰减后耦合到下混频器的输入端.在发射模式下,发射机和接收机以时分双工的方式工作.
2 图样转换的原理和算法
2.1 双线性插值的原理
理想情况下,可认为PRED、SQpred、DIST、SQdist4个图样都足够密,可以使PRED或DIST中任意一个四边形格子内部的非线性都很小.假定pred(·)是功放的预失真函数,能从功放的输出倒推到其输入.给定一个输入P以及4个相邻点A、B、C、D,并且这4个点构成逆时针围绕P的凸四边形的4个顶点时,当局域线性条件满足时下式近似成立:
pred(P)≈ (1-α)(1-β)pred(A)+α(1-β)pred(B)+
αβpred(C)+(1-α)βpred(D),
(1)
其中α、β是处于[0,1)之间的系数,并满足:
P=(1-α)(1-β)A+α(1-β)B+αβC+(1-α)βD.
(2)
在上例中,A、B、C、D被称作P关于pred(·)的4个有序的相邻点.只有对应某个给定的SQpred的PRED已知,并且此SQpred里对函数定义域里任意一个P都有4个相邻点A、B、C、D时,算法才可以应用.图4(a)中绘出了一般的情况.
构造出这样的PRED以后,下面主要的任务就是找到相邻点A、B、C、D和对应的系数α、β了.为了能使这个过程能容易完成,最简单的办法是令SQpred为方格,这就有:
(3)
如果把格子的大小定义为1.相应地,α、β也可以表示为:
(4)
在预失真器的硬件实现中,A、B、C、D可以根据P的最高位(Most Significant Bit, MSB)寻址得到,而α、β只需取P的最低位(Least Significant Bit, LSB)即可.图4(b)绘出了pred(·)的定义域里的格点取方格的特殊情形(SQpred的情形).
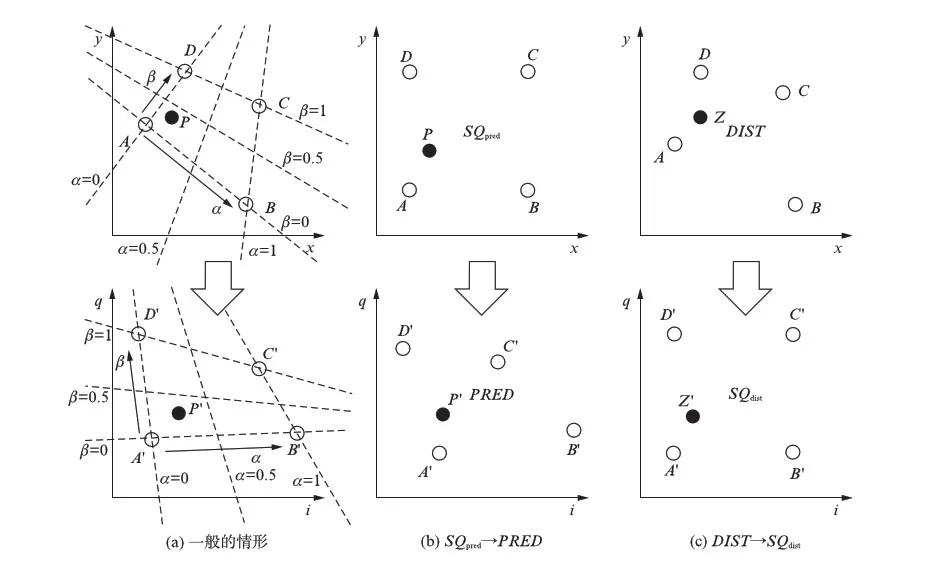
图4 插值的不同实现方法Fig.4 Different realizations of the interpolation
2.2 图样转换的原理
下一步就是获得预失真函数pred(·),或者等效地也可以用对应一个给定方格点SQpred的预失真图样来代替.
给定输入来测量功放的输出很容易.但给定输出要求功放的输入就难多了——除非测量和分析迭代进行,这正是文献[6]的做法.于是,我们提出用下面的间接法来获得想要的预失真对应关系:
(1) 测量对应某个给定的方格点SQdist的失真图样;
(2) 对PRED中每个要求的pred(P),求P在DIST中的4个相邻点并用内插法得到一个pred(P)的近似值.之后用这些pred(P)的近似值构造PRED.
上面(2)中用到的内插如图4(c)所示.注意此时DIST并非方格点,其格子是一般的凸四边形,这就导致了两个问题: 首先,如果不加优化,为了确定相邻点需要遍历DIST中的每一个格子,这样做的代价是每个格子至少要做8次乘法,而搜索的规模与DIST中的格子数成正比,这个方案很难让人接受;其次,当DIST的格子不是矩形时,求得α、β也并不容易.因此,寻求硬件可实现的图样转换算法是关键的一步.
2.3 硬件可实现的图样转换算法
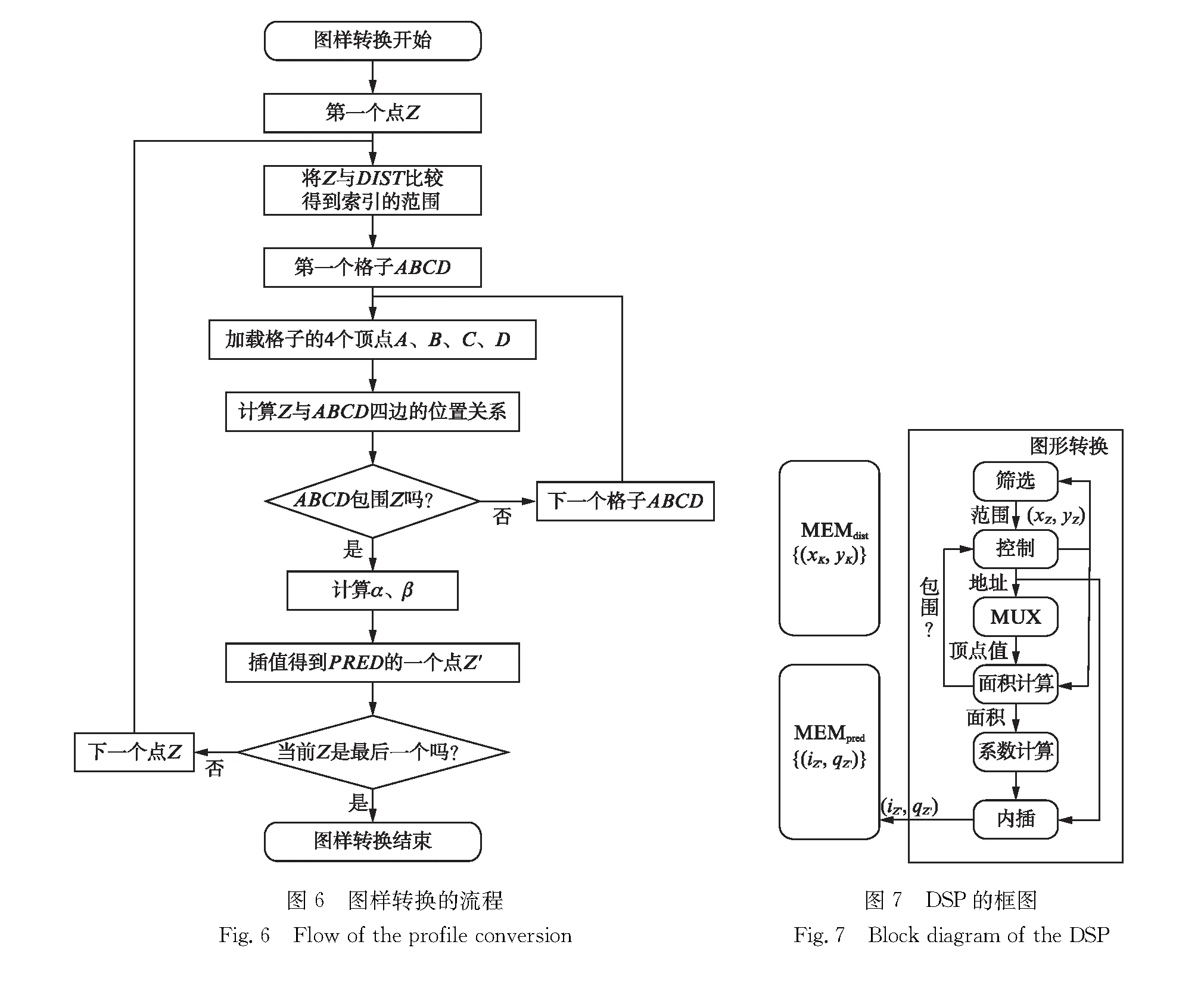
本设计提出了一种优化的两步式相邻点搜索方案来回避上述困难: 第一步,将P与DIST中的所有点(而非格子的边)相比较,根据得到的结果圈定一个粗略范围,即包含P的所在格ABCD的待定格集合{AiBiCiDi};第二步,再在{AiBiCiDi}内进一步搜索P的所在格ABCD.
那么第一步的实施就转化成了,对DIST中一个具体的待定格AiBiCiDi,如何定义以及判断其属于不属于{AiBiCiDi}.易知,P被AiBiCiDi包围的一个必要条件是,P的x坐标不超出AiBiCiDi4个顶点的x坐标范围,并且P的y坐标不超出AiBiCiDi4个顶点的y坐标范围.那么DIST中所有满足该必要条件的格子AiBiCiDi就组成了待定格集合{AiBiCiDi}.根据这种定义,筛选的判别式,如式(5)所示,是易于计算的:
(5)
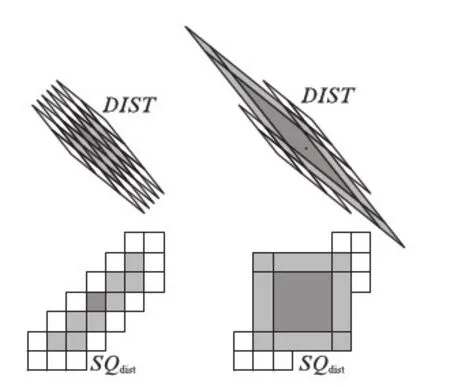
图5 待定格的合并Fig.5 Coalescence of the candidate cells
实际的算法实现仍然要求我们给出一个确定的待定格上限.理论上待定格当中可能存在两个格子的拓扑距离任意远,并且待定格的总数可能达到任意多.不过,当某两个待定格所夹的行(列)数超过1行(列)时(以相邻的两行所夹的行数为0,以此类推),中间的格子必然很扁(参见图5(a),其中深色格是所在格;浅色和深色格都是待定格).
表面上,任意多总数的待定格会使方格排除法并不能简化搜索格子的运算.不过可以再做一步近似: 考虑到存在两个待定格的拓扑距离很远时,中间很扁的格子可以合并而并不显著影响插值精度.合并的结果总可以使合并后的待定格形成不超过井字形3×3的9格.图5(b)绘出了合并后格子在DIST和SQdist中的对照情形.待定格合并后,排查的规模就减小到在不超过9个合并后的新待定格中找到1个所在格了,这个计算量是可以承受的.
接着,对每一个待定格AiBiCiDi,进一步检查AiBiCiDi是否包围P.仅当满足式(6)时AiBiCiDi包围P:
(6)
其中: ×表示两矢量的叉积;Ai、Bi、Ci、Di是格子逆时针顺序的4个顶点.搜索一直进行到找到一个包围P的AiBiCiDi为止,该AiBiCiDi就是所求的所在格ABCD.
一旦找到所在格,P相对于所在格的归一化位置系数由式(7)给出:
(7)
其中α、β是两个维度上的归一化位置系数,如图4(a)所示.
已知所在格的位置和归一化位置系数,预失真的近似值是:
(8)
2.4 图样转换的硬件实现
图样转换算法的流程图实现如图6所示.实现该流程的DSP由失真图样存储器(MEMdist)、图样转换器、预失真图样存储器(MEMpred)组成,如图7所示MEMdist把失真序列组织成DIST并储存之.训练序列结束时,系统控制器启动逐项计算PRED的序列,并将结果存在MEMpred里.内部循环和分支由有限状态机控制.
3 综合和仿真结果
3.1 综合
本设计采用TSMC 65 nm工艺实现,数字部分综合采用Synopsys Design Compiler和IC Compiler.数字部分所占面积为0.34 mm2.
3.2 仿真
系统的仿真涵盖了3种情况:
仿真Ⅰ是应用理想预失真图样在MatLab平台上的行为级仿真.预失真后带内误差是-39.83dBc,左右邻带误差都是-52dBc.
仿真Ⅱ是应用图样转换器生成的预失真图样在MatLab平台上的行为级仿真.预失真后带内误差是-34.87dBc,左右邻带误差分别是-43dBc和-44dBc.
仿真Ⅲ是应用图样转换器生成的预失真图样在Cadence平台上的布局前仿真.除了ADC采用行为级模型以加速仿真以外,整个系统在晶体管级进行仿真.仿真Ⅲ结果显示,针对7.2dB PAPR、40MHz带宽的LTE信号,在13.82dBm的发射信号功率下,系统可以将发射机的带内误差从-16.55dB降至-30.07dB.
在仿真Ⅲ中,预失真表的完整建立分为两步,即图样测量和图样转换.ADC工作在40MHz采样频率下时,图样测量占时13.6μs.图样转换约占时3μs,这取决于发射机失真图样的不同而略有差异.
4 结 语
本文提出了图样转换法来建立预失真系数表,以应用于基于查找表的双线性预失真器,可以很好地消除多比特正交数字发射机的复杂二维失真: 建立模式下发射机发射扫描信号,通过片上的接收通路测量耦合而得的输出信号,经数字信号处理单元计算得到预失真查找表.根据这种方法,文中给出了实际的设计实例.相较于前人提出的迭代测量法每一次预失真表的建立会在发射机和接收机都被占用的情况下持续约1ms,本文提出的图样转换法的最大优势是训练时间短.考虑图样测量的时间(13.6μs)小于LTE-TDD系统中发射机过渡时间(17μs),这意味着有可能在每个帧的发射之前都重新进行一次预失真表的建立,从而预失真表可以在通信过程中随时更新以紧跟发射机失真特性的变化而不需打断收发进程.
[1] WALLING J S, LAKDAWALA H, PALASKAS Y,etal. A Class-E PA with pulse-width and pulse-position modulation in 65 nm CMOS [J].IEEEJournalofSolid-StateCircuits, 2009,44(6): 1668-1678.
[2] NUYTS P A J, SINGERL P, DIELACHER F,etal. A fully digital delay line based GHz range multimode transmitter front-end in 65-nm CMOS [J].IEEEJournalofSolid-StateCircuits, 2012,47(7): 1681-1692.
[3] ZHAO Y, SHEN Y, XUE P,etal. An all-digital gigahertz Class-S transmitter in a 65-nm CMOS [J].IEEETransactionsonVeryLargeScaleIntegrationSystems, 2016,24(4): 1402-1411.
[4] YE L, CHEN J, KONG L,etal. Design considerations for a direct digitally modulated WLAN transmitter with integrated phase path and dynamic impedance modulation [J].IEEEJournalofSolid-StateCircuits, 2013,48(12): 3160-3177.
[5] LIANG P, WANG H, PENG C H,etal. Digital transmitter design for mobile devices [J].IEEECommunicationsMagazine, 2013,51(10): 114-123.
[6] WANG H, PENG C H, CHANG Y,etal. A highly-efficient multi-band multi-mode all-digital quadrature transmitter [J].IEEETransactionsonCircuits&SystemsIRegularPapers, 2014,61(5): 1321-1330.
FullyAutomaticPredistortionBasedonProfileInversionforMulti-bitCartesianTransmitters
SHENYilei,XUEPan,YEFeng,HONGZhiliang
(StateKeyLabofASIC&System,FudanUniversity,Shanghai201203,China)
The multi-bit Cartesian scenario, one of the most promising scenarios among the all-digital diversity of the transmitters, exhibits significant nonlinearity and requires complex 2D predistortion. As a partial solution to building the predistortion coefficients, iterative measurement has been proposed, but it is imperfect with respect to its lengthy procedure which takes around 1 ms. We propose a novel scheme of profile inversion to tackle the problems. Compared to iterative measurement, our scheme greatly reduces the setup time in the predistortion coefficients to less than 20 μs, while achieving predistorted in-band error of -30.07 dB with an LTE signal with 7.2 dB PAPR in pre-layout simulation. Not only does the present scheme save the time and power consumption in the predistortion process, but also it renders a real-time predistortion setup for multi-bit Cartesian transmitters practicable for the first time.
all-digital transmitter; multi-bit Cartesian power amplifier; 2D predistortion; profile inversion
0427-7104(2017)06-0725-07
2017-03-23
沈逸磊(1991—),硕士研究生;洪志良,教授,通信联系人,E-mail: zlhong@fudan.edu.cn.
TN4
A

