上游水电站围堰漫顶溃决条件下施工中期度汛水位数值模拟
,
(中国电建集团 成都勘测设计研究院有限公司, 成都 610072)
上游水电站围堰漫顶溃决条件下施工中期度汛水位数值模拟
张超,蒋陶
(中国电建集团 成都勘测设计研究院有限公司, 成都 610072)
比邻梯级水电站同期建设条件下,若上游水电站围堰遭遇超标洪水发生漫顶溃决,将严重威胁下游水电站施工中期度汛的安全,因此,对度汛水位变化过程进行数值模拟具有重要意义。基于水动力学理论方法,建立了上游水电站围堰漫顶溃决条件下中期度汛水位变化过程模拟的数学模型,并将该模型应用于大渡河流域某相邻梯级水电工程实例中。通过不同计算方案的数值模拟分析,结果表明:该模型及方法是可行的、有效的;相比于基于天然洪水流量的计算方法,所提方法更加贴近工程实际,且度汛最高水位明显增大,因而更有利于工程安全。研究成果为上游水电站围堰挡水条件下的施工中期度汛方案决策及防洪应急预案的制定提供了重要的理论依据。
梯级水电站;施工中期度汛水位;围堰漫顶溃决;数值模拟;水动力学理论
1 研究背景
高坝水电工程的施工导流贯穿建设全过程,其施工中期度汛不仅直接关系工程本身和施工人员的安全,而且影响工程的管理、进度、发电等社会经济效益[1-3],因此,开展中期度汛挡水位的数值模拟计算研究具有重要的理论意义和工程应用价值。随着我国西南诸多流域水电站的梯级滚动开发,任金明等[4]探讨了下游梯级水库对上游水电站施工导截流的影响。张超等[5-8]对梯级建设条件下的施工导流风险分析理论进行了探讨。在溃堰洪水计算及应用方面,李军等[9]对锦屏二级水电站进行了施工期的围堰溃堰洪水分析。刘林等[10]对溃坝洪水研究进行了总结,并提出梯级溃坝洪水的相关研究较少。
然而,梯级水电站施工导流计算分析理论有待进一步完善。由于比邻梯级水电站开发建设时序的差异,存在上游水电站处于初期围堰挡水阶段,而下游水电站处于施工中期度汛阶段的情况。此时,下游水电站施工中期度汛标准较上游水电站初期围堰挡水标准更高,而上游水电站可能遭遇超标洪水的情况,若上游水电站围堰漫顶溃决,势必对下游水电站的施工中期度汛造成严重的影响。
因此,本文以大渡河流域某相邻梯级水电站工程为研究对象,基于水动力学理论方法,全面考虑上游水电站围堰漫顶溃决过程及溃堰洪水演进过程,对下游水电站中期度汛水位的变化过程进行数值模拟分析,为上游水电站初期围堰挡水条件下的施工中期度汛方案决策及溃堰应急预案的制定提供必要的理论依据。
2 工程概况及计算方案
2.1 工程概况
西南地区大渡河流域上游水电站A采用坝式开发,拦河坝为混凝土面板堆石坝,最大坝高达223.50 m,工程初期导流采用断流围堰挡水、隧洞导流的导流方式,初期导流标准为50 a一遇。上游围堰为土石围堰,堰顶设计高程1 742.50 m,堰顶宽度12.00 m,迎水面边坡1∶2.0,背水面边坡1∶1.8,库区回水长度约12 km,库容约0.3亿m3。围堰混凝土防渗墙施工平台高程1 706.00 m,防渗墙厚度1.00 m。B水电站是A水电站下游相邻梯级,拦河大坝为砾石土心墙堆石坝,最大坝高240.00 m,距A水电站坝址约36.00 km,中期度汛标准为100 a一遇。河道洪水以上游来水为主,区间流量较小。
根据2个水电站施工进展,某年汛期上游A处于初期导流时段,而下游B的汛前填筑高程H=1 534.50 m,已超过围堰高程而处于中期度汛的时段。此时,正常运行时,上游A围堰导流不会对下游B水电站施工造成不利影响,但下游B中期度汛标准较上游A初期挡水标准高,下游B中期度汛标准对应的洪水过程实际上为上游A水电站遭遇的超标准洪水,上游A施工围堰若发生漫顶溃决,库区水体突然下泄,将形成较大的洪峰向下游传播,势必严重威胁到下游B的坝体及施工人员的安全。
2.2 计算方案
本文主要对上游A围堰漫顶溃决条件下下游B中期度汛水位变化过程进行数值模拟分析,以期为中期度汛方案决策及防洪应急预案的制定提供必要的数据,拟定的计算方案如下:
(1) 计算分析对比在相同来流情况下,上游A围堰漫顶溃决与无上游A围堰的洪水演进过程。模拟过程中,若下游B坝前水位变化过程中超过坝体高程,假定水流从坝顶溢流而过。
(2) 计算分析在上游A围堰高度不变,且溃口发展过程相同条件下,上游A不同频率洪峰与下游B度汛最高水位的关系。模拟过程中,假定下游B仅靠导流洞泄流。
(3) 求解设计标准下下游B的中期度汛最高水位hmax。假设H为下游B汛前填筑高程,则下游B的中期度汛方案制定分2种情况:①若H>hmax,则下游B填筑高程满足防洪度汛要求,采用大坝拦洪度汛方案,汛期可正常施工;②若H≤hmax,则下游B需做好坝体过水保护,并提前制定必要的洪灾应急预案,或者坝体抢筑措施至拦洪高程。
3 数学模型
土石围堰溃决过程模拟由3部分组成,包括:①溃口模拟;②围堰溃决下泄流量模拟;③溃口下泄洪水的河道演进模拟。
3.1 溃口和下泄流量模拟
溃口模拟主要是对溃口形状和溃口扩大演变过程进行模拟。溃口的形状通常概化为矩形、三角形或梯形,其尺寸由最终溃口底宽、溃口边坡和最终溃口底部高程来决定。DAMBRK模型的溃口流量模拟方法所需参数较少,应用较为简单方便,在许多工程中得到了应用,并取得了良好的效果。因此,本文在溃堰洪水计算中主要参照DAMBRK模型,结合经验和其他失事大坝的数据给定溃口开始到最后终止的时间和溃口的最终尺寸与形状进行模拟。
围堰溃决后,下泄流量由溃口下泄流量和导流泄水建筑物泄流流量2部分组成。
3.2 溃堰洪水演进数学模型
3.2.1 模型控制方程
对于一维明渠水流,如果假定为静水压力分布和小底坡,则可用圣维南方程组描述,其中水流连续方程为
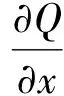
(1)
运动方程为
(2)
式中:x为流程(m);Q为流量(m3/s);Z为水位(m);g为重力加速度(m/s2);t为时间(s);A为过水断面面积(m2);R为断面水力半径(m);nc为糙率系数。
3.2.2 方程离散
模型采用有限差分法进行离散求解,并引入有限体积的思想,运动方程中对流项采用一阶迎风格式离散,根据胡晓张等[11]的研究,这一格式在求解非线性对流及对流扩散方程时具有较高的精度。
对时间偏导项∂Q/∂t和∂A/∂t采用向前差分格式,对流项采用一阶迎风格式,对时间偏导项的处理采用蛙跳格式,这样上述方程可离散为:
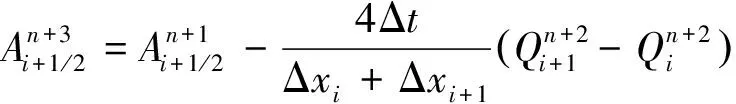
(3)
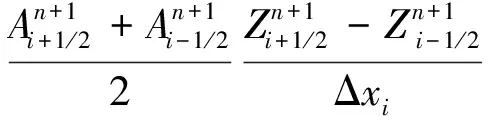
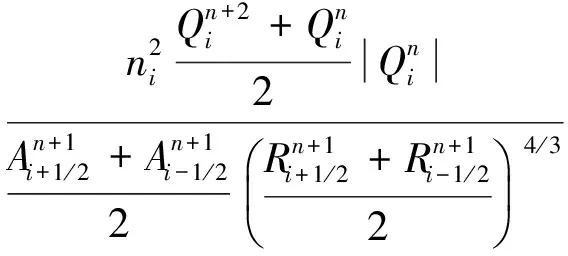
(4)

4 数值模拟分析
4.1 计算资料
4.1.1 地形资料
模型模拟的范围为从上游A坝址上游约12 km至下游B坝址,计算河段总长51.7 km,共取计算断面42个。其中上游A库区河段长12.2 km,布设有10个断面,下游B坝址至上游A坝址区间河段长39.5 km,布设有32个断面。
4.1.2 模型计算初始条件和边界条件
初始条件:本模型在计算非恒定流过程前,先假设一恒定流计算得到的各断面水位和流量作为非恒定流计算的初始条件。
边界条件:由于模型模拟的范围包括上游A库区河道和上游A围堰至下游B围堰区间河道,模型计算上边界条件为特征频率下上游A入库洪水流量过程,溃堰计算时上游A导流洞泄流曲线作为内边界条件处理,出口边界为下游B中期度汛的导流洞泄流曲线。
4.2 计算工况
溃堰洪水受多种因素影响,如溃堰历时、上游来流量、溃堰时坝前水位、溃口发展过程等,本次计算仅选定一种溃堰方案进行模拟,同时,为分析溃堰洪水对下游梯级水电站中期度汛的影响,计算了相同来流情况下天然河道洪水演进情况进行对比分析。
下游B中期度汛标准为100 a一遇洪水,电站之间区间流量较小可不考虑。因此,针对上游A发生100 a一遇洪水(Q=6 060 m3/s)进行溃堰计算分析,溃堰时,堰前水位选取为堰顶高程1 742.50 m,溃堰历时取值2 h,溃决终止时溃口底宽、底高程和边坡系数分别为100 m,1 715.00 m,1.0。
河道糙率采用实测水面线推算得出的成果,其变化范围为0.05~0.07。
4.3 模拟过程
本文采用的溃堰洪水数学模型在上游A的初期围堰溃堰洪水计算中分为4个阶段:
(1) 起算后的一段时间内,库尾上游来流给定为一恒定基流流量,由此计算非恒定流计算阶段开始时刻的沿程流量和水位。当计算得到沿程各断面(包括坝下游断面)流量相等时,转入非恒定流计算阶段。
(2) 库尾上游来流按对应的设计洪水标准过程加入。由于上游来流随时间变化,库区流量和水位随之变化。涨水过程中,导流洞泄流流量小于上游来流流量,水库水位上涨。进入围堰下游河道的流量为导流洞流量和过围堰流量之和。
(3) 当堰前水位继续上涨达到该工况设定的溃堰发生的水位时,堰体出现溃口。溃口流量由宽顶堰流量公式计算,同时导流洞的下泄流量由其水位流量关系曲线确定。
(4) 溃口发生后,上游入库洪水按设计过程继续加入,溃口尺寸随时间扩大,通过溃口的流量不断增加(进入围堰下游河道的流量为溃口流量和导流洞流量之和)。水库水位开始下降,直到泄空,计算结束。
以上4个阶段是连续进行的。数学模型输出的计算结果为计算河段所有断面的流量和水位变化过程。笔者重点分析的是下游B断面的流量和水位变化过程,同时为对计算结果进行更详细的描述,本文另外在B水电站库区沿程选取了8#和17#以及上游A围堰29#断面的流量和水位变化过程进行分析。
4.4 计算成果
4.4.1 无上游A围堰情况下洪水计算成果
为便于将上游A围堰在相同来流情况下溃堰洪水计算的结果与无A围堰的情况下天然洪水演进结果进行比较,评估上游A溃堰可能造成的影响,首先对无A围堰的情况下遭遇100 a一遇洪水进行了洪水演进计算,下游出口水位由B水电站导流洞泄流曲线控制。所选各特征断面处计算得到的最大流量和最高水位结果如表1所示。
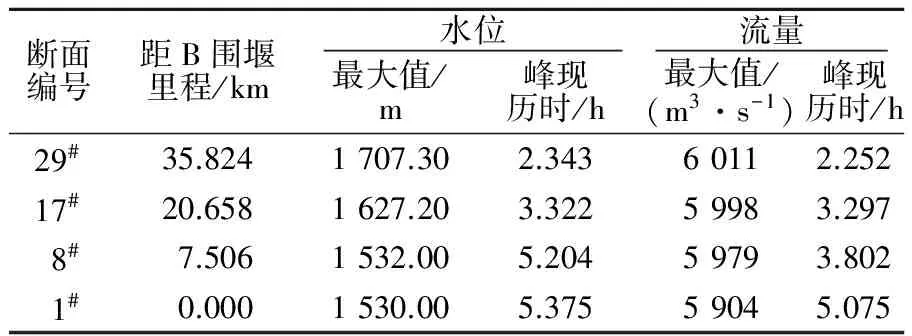
表1 无A围堰情况下计算成果Table 1 Calculation results of maximum flow and peakwater level in the absence of cofferdam A
4.4.2 上游A溃堰洪水计算成果
溃堰洪水计算模拟当上游A围堰发生漫顶溃决时溃堰洪水向下游的演进过程,沿程各典型断面处计算得到的最大流量和最高水位结果见表2,沿程各特征断面洪水流量过程见图1。
由表1计算成果可知,无A围堰的情况下洪水流量沿程衰减较小,流量峰现时间略早于水位峰现时间。
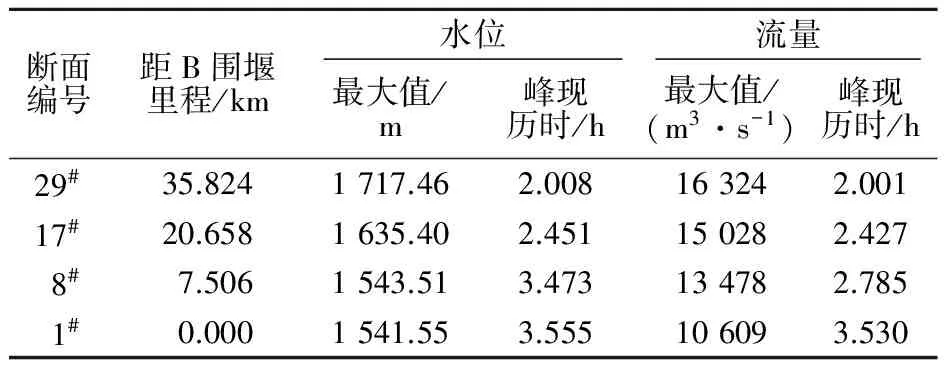
表2 A围堰溃堰情况下计算成果Table 2 Calculation results of maximum flow and peakwater level in the presence of cofferdam break
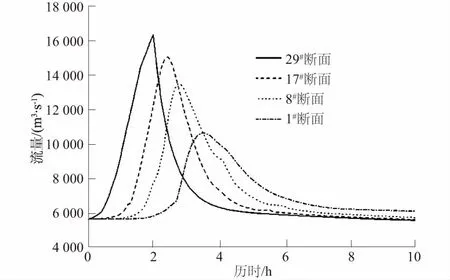
图1 溃堰情况下各特征断面流量过程线Fig.1 Process lines of flow at characteristic sections in the case of cofferdam break
表4溃堰洪水与无A围堰天然洪水计算成果比较
Table4ComparisonbetweencalculationresultswithcofferdambreakandthoseintheabsenceofcofferdamA

断面编号距B围堰里程/km水位峰值/m流量峰值/(m3·s-1)水位峰现时间/h无A围堰A溃堰差值无A围堰A溃堰差值无A围堰A溃堰差值29#35.8241707.301717.4610.16601016324103142.3432.008-0.33517#20.6581627.201635.408.2060001502890283.3222.451-0.8718#7.5061532.001543.5111.5159801347874985.2043.473-1.7311#0.0001530.001541.5511.5559001060947095.3753.555-1.820
由表2计算成果可知,流量峰现时间略早于水位峰现时间。当上游A发生溃堰时,溃口最大流量为16 324 m3/s,甚至大于该河段PMF(可能最大洪水)洪水流量。溃堰洪水在演进过程中存在洪峰衰减现象,当溃堰洪水演进至溃口下游约15 km处的17#断面处时洪峰流量为15 028 m3/s,较溃口衰减7.9%;当溃堰洪水演进至溃口下游约28 km处的8#断面处时洪峰流量为13 478 m3/s,较溃口衰减17.4%;当溃堰洪水演进至溃口下游约36 km处的下游B围堰断面处时洪峰流量为10 609 m3/s,较溃口衰减了35.0%。
4.4.3 不同频率洪峰与下游B最高水位关系
本节主要研究上游A不同频率洪水洪峰与下游B度汛最高水位的关系,施工洪水过程模拟采用按峰值放大典型洪水过程线的方法。计算过程中,洪峰流量超过上游A围堰设计标准后,认为上游A围堰发生漫顶溃决,并假设下游B的大坝填筑高度足够高,仅靠导流洞宣泄洪水,计算成果如表3所示。同时,根据计算模拟成果绘制上游A洪水洪峰流量与下游B最高度汛水位的关系曲线,如图2所示。

表3 上游A不同频率洪水洪峰与下游B度汛最高水位的关系Table 3 Relationship between flood peak of differentfrequencies at A and maximum flood level at B
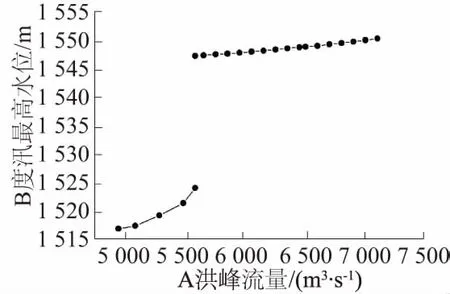
图2 A洪峰流量与下游B度汛最高水位的关系曲线Fig.2 Relationship between flood peak at A and maximum flood level at B
4.5 成果讨论
(1) 为更好地说明上游A溃堰洪水对下游B造成的影响,将溃堰洪水计算结果与无A围堰的天然洪水计算情况进行了比较分析,计算得到的下游各特征断面的水位峰值、流量峰值及水位峰现时间列于表4中。
从表4计算成果可知,洪水演进至17#断面时,溃堰洪水洪峰流量为15 028 m3/s,较无A围堰天然洪水大9 028 m3/s,峰现时间也比无A围堰的天然洪水早0.871 h,水位峰值高8.2 m;当洪水演进至1#断面,即下游B坝前时,溃堰洪水流量衰减为10 609 m3/s,仍大于无A围堰天然洪水5 900 m3/s,水位峰现时间早于无A围堰天然洪水1.820 h,溃堰洪水在B坝前的水位峰值为1 541.55 m,高于无A围堰天然洪水水位峰值11.55 m。
(2) 通过表3和图2曲线整体趋势可以看出,下游B度汛最高水位与洪峰呈正相关关系,当上游A遭遇围堰设计标准对应洪峰流量5 590 m3/s时,若考虑不溃堰,此时下游B度汛最高水位1 524.08 m;若考虑围堰漫顶溃决,此时下游B度汛最高水位1 547.26 m,表明溃堰较不溃情况对应的下游B度汛最高水位大幅度增加,曲线在此处产生了突变;之后的曲线趋势表明,洪峰流量超过上游A围堰设计标准后,上游A围堰发生漫顶溃决,下游B度汛最高水位随上游A洪峰流量增加仍逐渐增大,但变化幅度不明显。
(3) 根据表3计算成果,由于下游B汛前填筑高程达H=1 534.50 m,而通过本文提出的方法求解设计标准下下游B的中期度汛最高水位hmax=1 548.01 m,即H (4) 通过对上游A围堰溃口发展过程、溃堰洪水在下游河道的演进、下游B中期度汛水位进行模拟计算,可为溃堰应急预案的制定提供必要的数据。建议施工期结合水情预报信息,加强监测,一旦发生超标洪水,迅速通知下游河道两岸居民及下游B施工人员,启动应急预案,确保人员安全、有序撤离,将人民生命财产损失降到最低。 (1) 针对比邻梯级水电站建设存在的上游水电站处于初期围堰挡水阶段,下游水电站处于施工中期度汛阶段的情况,基于水动力学理论方法,对下游水电站中期度汛水位进行数值模拟分析。 (2) 若仍按照度汛标准对应的天然洪水流量进行施工中期度汛方案的设计显然是偏危险的,实际度汛阶段考虑上游水电站围堰漫顶溃决洪水过程的影响并进行准确量化十分必要。 (3) 通过数值模拟可获得度汛水位变化过程,成果可为下游水电站中期度汛方案的制定及防洪应急预案的制定提供重要的数据支撑。 [1] 徐唐锦,李 蘅,马永锋.坝体度汛及导流泄水建筑物洪水标准研究与探讨[J].人民长江,2011,42(16):69-72. [2] 钟登华,常昊天,刘 宁,等.高堆石坝施工过程的仿真与优化[J].水利学报,2013,44(7):863-872. [3] 张 超,胡志根.高堆石坝中期度汛挡水风险率估计[J].水科学进展,2014,25(6):873-879. [4] 任金明,蔡建国,胡志根,等.下游水库对上游梯级电站施工导截流的影响[J].武汉大学学报(工学版),2011,44(3):331-334. [5] 张 超,胡志根,刘 全.梯级施工导流系统整体风险分析[J].水科学进展,2012,23(3):396-402. [6] 张 超,胡志根,刘 全.上游水电站控泄条件下施工导流风险分析[J].水利学报,2012,43(11):1328-1333. [7] 刘 全,胡志根,任金明,等.梯级建设环境下水电工程施工导流风险分析[J].水力发电学报,2014,33(1):147-153. [8] 张 超,胡志根,李家亮,等.上游水电站初期导流条件下下游水电站施工导流风险分析[J].水电能源科学,2014,32(6):120-123. [9] 李 军,任金明,刘 全,等.锦屏二级水电站过水围堰溃堰风险分析[J].水电能源科学,2011,29(4):102-104. [10]刘 林,常福宣,肖长伟,等.溃坝洪水研究进展[J].长江科学院院报,2016,33(6):29-35. [11]胡晓张,张小峰.溃坝洪水的数学模型应用[J].武汉大学学报(工学版),2011,44(2):178-181. Numerical Simulation of Flood Level During Mid-stage Construction ofHyropower Station in the Presence of Overtopping Failure ofUpstream Cofferdam ZHANG Chao, JIANG Tao (Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China) Simulating the flood level at downstream cascaded hydropower station in mid-stage construction is of critical significance once the adjacent upstream cofferdam in simultaneous construction encounters standard-exceeding flood and overtopping failure which severely threatens the construction safety of the downstream plant. In line with the hydrodynamic theory, a mathematical model is built for simulating the process of water level variation in mid-stage construction period under the condition of cofferdam break of the upstream cofferdam. The model is applied to two adjacent cascade hydropower stations in Dadu River valley. Simulation results suggest that the model is feasible and effective. Compared with the calculation method based on natural flood flow, the proposed method is closer to the actual situation, and the obtained maximum water level in flood season is apparently larger, which is more conducive to the safety of the project. This study provides an important theoretical basis for the decision-making and flood emergency planning of downstream plant in mid-stage construction with cofferdam in the upstream. cascaded hydropower station; flood water level in mid-stage construction; overtopping failure of cofferdam; numerical simulation; hydrodynamic theory 2016-09-12; 2016-11-08 成都勘测设计研究院有限公司科研资助项目(P228-2014);成都勘测设计院研究有限公司青年科技基金项目(P294-2015) 10.11988/ckyyb.20160940 TV551.1 A 1001-5485(2018)01-0052-05 (编辑:陈 敏)5 结 语

