基于核密度估计的AM-MCMC算法在径流模拟中的应用

， ，，

(1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室, 南京 210029； 2.中国科学院南京地理与湖泊研究所 中国科学院流域地理学重点实验室，南京 210008)

基于核密度估计的AM-MCMC算法在径流模拟中的应用

童坤1，2，刘恒1，耿雷华1，徐澎波1

(1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室, 南京 210029； 2.中国科学院南京地理与湖泊研究所 中国科学院流域地理学重点实验室，南京 210008)

无资料或资料稀缺地区的径流概率模拟， 是目前水文研究难点问题之一。 基于此, 利用Kernal核密度估计法估算出流量的月径流概率密度函数， 采用基于自适应采样算法(Adaptive Metropolis algorithm， AM)的马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)模拟方法求解， 最后给出月径流量的模拟预测。 实例表明基于Kernel核密度估计的AM-MCMC算法模型计算结果精度较高， 有良好的应用价值， 可在资料较少地区推广使用。

径流模拟；概率分布；核密度估计； AM-MCMC算法；罗岙水库

1 研究背景

水文变量概率密度函数复杂且未知，某一指定概率分布与真实分布存在着差异。目前对于水文概率密度估计主要有参数估计和非参数估计2种类型：参数估计法是密度函数结构，此时的密度估计就是传统的参数估计问题(如P-Ⅲ型分布已知求cv,cs)；非参数估计是密度函数未知，仅从既有的样本出发得出密度函数的表达式。

非参数估计方法主要有核密度法、直方图法、样条函数法以及混合概率密度法等，其中核密度估计是较常用和有效的方法。本文提出基于Kernel核密度估计的AM算法模型，通过Kernel估计法，估计出坝址月径流量的密度分布，然后利用AM算法对其进行模拟。使用核函数方法进行初始概率密度估计，推导出条件概率密度估计，以分布权重为抽样概率计算出均值、方差，并由此计算出模拟值。基于AM算法的马尔可夫链蒙特卡罗(MCMC)模拟不再依赖于参数的推荐分布也不受参数的先验区间的影响,能够保证算法的遍历性和较高的抽样效率[1]。与过去单纯的马尔可夫链蒙特卡罗方法用于计算月径流量过程相比，该方法精度更高，可用于进一步推广应用。

2 核密度估计法

核密度估计法(Kernel density estimation)又名Parzen窗(Parzen window)，由Rosenblatt[2](1956)和Parzen[3](1962)提出，在概率论中被用来估计未知随机变量的密度函数。核密度估计的概念是直方图概念的推广。Scott等[4](1996)证明当平均平移直方图(Averaged Shifted Histogram,ASH)的直方数量趋于无穷时，直方图便趋于Kernel核密度。1994年，Ruppert等[5]利用数据集密度函数聚类算法对其进行修正。1996年我国学者崔恒建等[6]引入核密度估计法对直径分布进行拟合，2000年开始应用到我国各个研究领域[7-9];唐林俊等[10](2006)在单变量核密度估计的基础上建立了风险价值预测的预测模型；王文圣等[11](2001)首次将单变量核密度估计用于径流随机模拟。核密度估计法由于其从样本出发研究现有数据的分布特征而受到高度重视和应用。相对于其他方法，核密度估计法主要优点就是对数据分布不附加任何假定，不需要了解数据分布的先验知识。

设X1,X2,…，Xn是密度函数为f(x)的未知总体的独立同分布的随机变量，Kernel核密度估计为

(1)

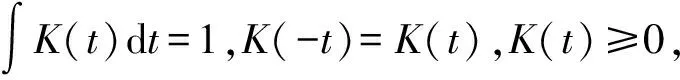
(2)

多元函数核密度估计的是通过将一维核函数连乘得到乘积核函数，利用乘积核函数进行估计。乘积核函数表达式为

(3)

式中:xij是第j个分量的第i个观测值;hd为维度d下的窗宽。

本文只涉及到一个变量，因此使用式(1)进行计算。

从Kernel密度估计的表达式可以看出，该方法是通过将核函数K分别置于以样本Xi为中心处，然后计算此时所有点的函数值，最后对其进行平均。常用的K(t)有正态函数、三角核函数、双权重核函数、三权重核函数、Epanechnikov核函数等，如表1所示。

表1 典型核函数表达式Table 1 Typical expressions of kernel function

3 窗宽的确定(LSCV法)

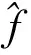
目前，有关窗宽选择的方法可分为以下几种：交错鉴定方法、惩罚函数法、插入法以及对比方法[12-15]。常用的是插入法，即把未知函数的估计插入到渐近公式里以选择最佳窗宽。本文采用固定窗宽法，固定窗宽就是在每一个拟合点取等窗宽，基于最小平方差(LSCV)的思想，根据积分均方误差(MISE)最小，求出最优窗宽。MISE为

(4)

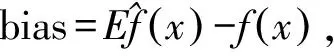
(5)

(6)

(7)

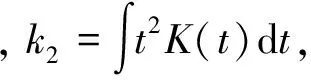
(8)

因此，如需MISE最小，则AMISE达到最小即可，对AMISE求一阶导数并令其等于0，求得最优窗宽h*为

(9)

4 AM-MCMC抽样算法

4.1 马尔可夫链蒙特卡罗方法(MCMC)

马尔可夫链蒙特卡罗方法(MCMC)通过构造马尔可夫链，使得计算出的马尔可夫链稳定分布为要求的目标分布，也就是说希望通过利用马尔可夫链取得的样本就可以直接当成是目标分布中产生的样本来利用，其核心思想是建立转换函数使得无论初始值取何值，最后马尔可夫链都会收敛到目标分布。马尔可夫链蒙特卡罗方法作为一种随机模拟方法，早已被应用到物理、天文、气象、通信等各个领域，MCMC的关键是如何选择推荐分布转移密度使采样更加有效，常用的方法有Gibbs采样[16]、Metropolis-Hasting取样[17]和自适应取样[18](Adaptive metropolis-hasting method，AM算法)。这3种抽样方法中，只有AM算法不依赖于事先的推荐分布且收敛速度较快，因此本文采用AM算法。

4.2 收敛判断准则

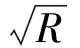
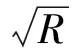
(10)

其中

(11)

(12)

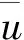
5 误差判别

选取相对误差与均方差作为计算结果的判别函数，其中，相对误差公式为

(13)

均方根误差RMS(Root Mean Squared Residual)公式为

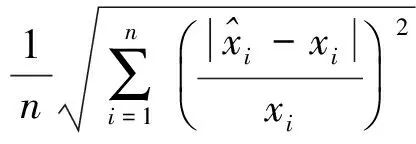
(14)

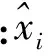
因为RMS计算公式中没有考虑拟合来水量变化幅度对模型精度的影响，因此，引入另外一个更加准确的判别参数:标准化残差均方根Normalized RMS，其计算公式为

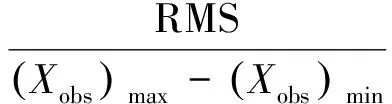
(15)

式中:(Xobs)max为观测值中的极大值;(Xobs)min为观测值中的极小值。

6 案例应用

罗岙水库位于健跳港上游，见图1。坝址以上集水面积12.3 km2，多年平均入库水量约1 100万m3。该水库为1969年动工，1979年完工的以灌溉为主，兼顾防洪、供水的小型水库，由六敖镇镇政府管理。2005年，该水库被列为浙江省“千库保安”建设计划和台州市重点工程，开展加高加固。罗岙水库工程枢纽建筑物由拦河坝、溢洪道、输水隧洞等组成。除险加固以前，水库总库容478万 m3，正常蓄水位6.9 m，相应库容339万 m3，死水位1.50 m，相应库容12万 m3，兴利库容327万 m3。

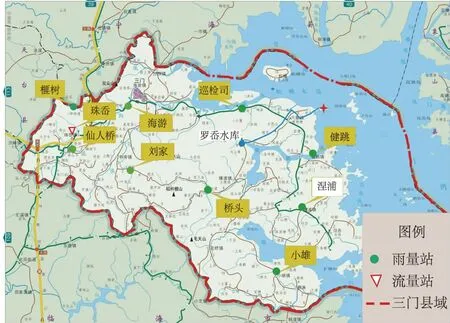
图1 罗岙水库及雨量、流量站分布示意图Fig.1 Map of Luo’ao reservoir and distribution of rainfall and discharge gauging stations

根据海游站1952—2006年共55 a逐月降水量与蒸发量资料，对罗岙水库坝址长系列来水月径流量进行模拟分析。坝址长系列历年逐月平均径流量见图2。

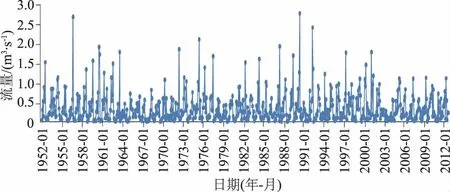
图2 罗岙水库坝址逐月平均径流量变化过程曲线Fig.2 Monthly average flow at the dam site of Luo’ao reservoir

对1956—2006年平均月径流量进行Kernel估计，假设预先给定的概率密度分布是正态分布，则核函数K(t)选择正态分布函数，在每个样本处利用核函数进行该处的密度估计，然后样本间进行差值得到连续的估计密度曲线。图3是抽样样本均值与方差轨线图，可以看出所取随机数4 000个以后基本趋于稳定。

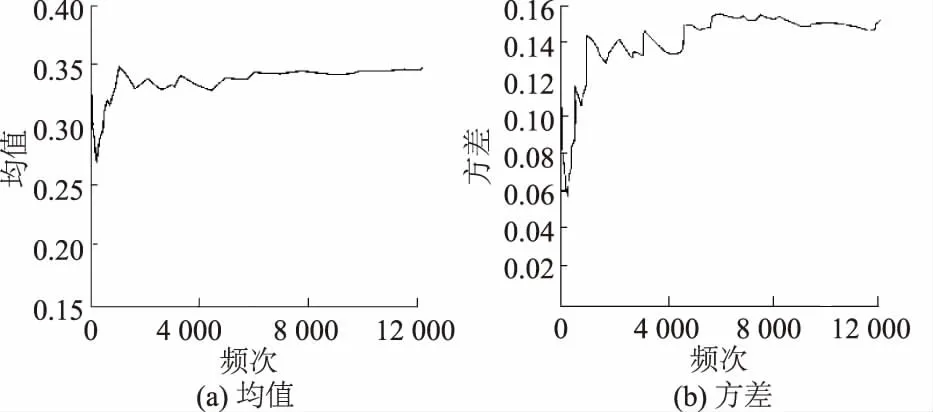
图3 均值方差轨迹线Fig.3 Trajectory of mean value and variance

利用得出的密度分布，结合AM算法对其进行抽样，设定抽样次数50 000次。根据LSCV法，通过多次拟合计算，最终确定窗宽h=0.01，频率直方图及理论概率密度曲线如图4，可见样本的频率直方图与理论密度曲线拟合很好。

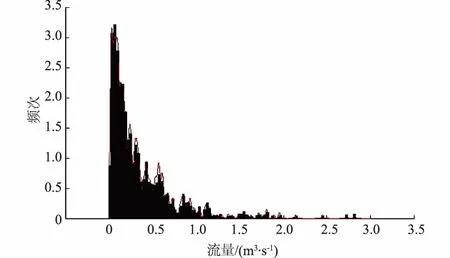
图4 概率密度分布Fig.4 Distribution of probability density

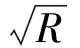
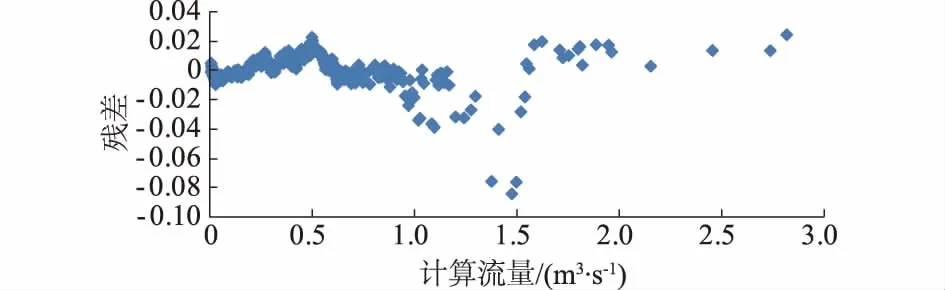
图5 残差分布Fig.5 Distribution of residual

对水库坝址的实际月径流量进行模拟分析，如图6所示，根据模拟结果计算得出RMS=0.48%,Normalized RMS=0.002%，说明所采集的样本合理，可以用来对水库径流量进行模拟计算。

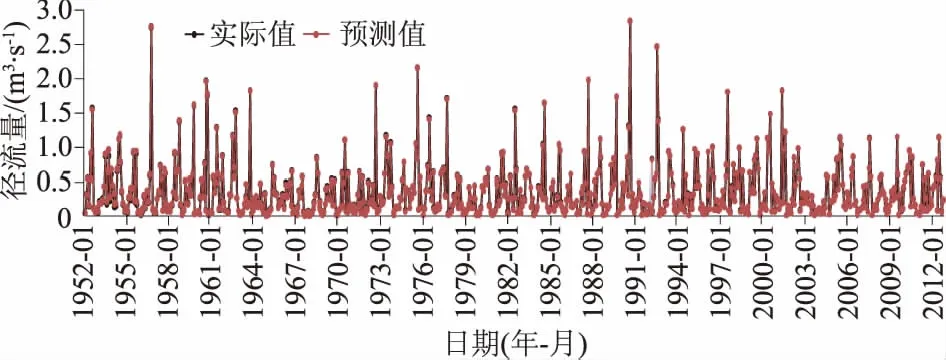
图6 坝址月径流量拟合曲线Fig.6 Curve fitting of monthly runoff at dam site

7 结 语

本文推荐的核密度估计法不需要事先了解模型的一系列参数，且基于AM算法的MCMC抽样模型无需预先给定推荐分布，不依赖于过去的经验，遍历性好、适应性强，该方法对于资料较少的地区可以进行很好的应用。从案例的实际应用中可以看出，基于核密度估计的AM-MCMC算法具有较高的计算精度，利用该模型计算出来的长系列水库月径流量与实测值差异不大，标准化残差均方根仅为0.002%，可以用于实际应用中估计水库的水文风险。不过本文对于核密度估计中的窗宽采用固定窗宽的办法，如何选择最优窗宽优化核密度估计，提高模拟的精度是下一步要研究的对象。

[1] 邢贞相, 芮孝芳, 崔海燕,等. 基于AM-MCMC算法的贝叶斯概率洪水预报模型[J]. 水利学报, 2007, 38(12):1500-1506.

[2] ROSENBLATT M. Remarks on Some Nonparametric Estimates of a Density Function[J]. Annals of Mathematical Statistics, 1956, 27(3): 832-837.

[3] PARZEN E. On Estimation of a Probability Density Function and Mode[J]. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.

[4] SCOTT D W, WHITTAKER G. Multivariate Applications of the ASH in Regression[J]. Communications in Statistics—Theory and Methods, 1996, 25(11): 2521-2530.

[5] RUPPERT D, CLINE D B. Bias Reduction in Kernel Density Estimation by Smoothed Empirical Transformations[J]. The Annals of Statistics, 1994:185-210, doi: 10.1214/aos/1176325365.

[6] 崔恒建, 王雪峰. 核密度估计及其在直径分布研究中的应用[J]. 北京林业大学学报, 1996,18(2):67-72.

[7] 刘 锐, 胡伟平, 王红亮, 等. 基于核密度估计的广佛都市区路网演变分析[J]. 地理科学, 2011,31(1):81-86.

[8] 赵 渊, 沈智健, 周念成, 等. 基于序贯仿真和非参数核密度估计的大电网可靠性评估[J]. 电力系统自动化, 2008,32(6):14-19.

[9] 凌建国, 刘尔琦, 梁海燕, 等. 基于核密度估计的红外目标提取方法[J]. 红外与毫米波学报, 2006,25(6):434-438.

[10] 唐林俊, 杨 虎, 张洪阳. 核密度估计在预测风险价值中的应用[J]. 数学的实践与认识, 2006,35(10):29-35.

[11] 王文圣, 丁 晶. 单变量核密度估计模型及其在径流随机模拟中的应用[J]. 水科学进展, 2001,12(3):367-372.

[12] JONES M C, MARRON J S, SHEATHER S J. A Brief Survey of Bandwidth Selection for Density Estimation[J]. Journal of the American Statistical Association, 1996, 91(433): 401-407.

[13] SAIN S R, BAGGERLY K A, SCOTT D W. Cross-validation of Multivariate Densities[J]. Journal of the American Statistical Association, 1994, 89(427): 807-817.

[14] BOLANCÉ C, GUILLEN M, NIELSEN J P. Kernel Density Estimation of Actuarial Loss Functions[J]. Insurance: Mathematics and Economics, 2003, 32(1): 19-36.

[15] FUKUNAGA K, HOSTETLER L. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1): 32-40.

[16] SMITH A F, ROBERTS G O. Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1993:3-23, doi: 10.2307/2346063.

[17] CHIB S, GREENBERG E. Understanding the Metropolis-Hastings Algorithm[J]. The American Statistician, 1995, 49(4): 327-335.

[18] HAARIO H, SAKSMAN E, TAMMINEN J. An Adaptive Metropolis Algorithm[J]. Bernoulli, 2001, 7(2): 223-242.

[19] GELMAN A, RUBIN D B. Inference from Iterative Simulation Using Multiple Sequences[J]. Statistical Science, 1992, 7(4): 457-472.

AM-MCMC Algorithm for Runoff Simulation ModelBased on Kernel Density Estimation

TONG Kun1,2, LIU Heng1, GENG Lei-hua1, XU Peng-bo1

(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China; 2.Key Laboratory of Watershed Geographic Science, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, China)

The simulation of runoff probability in an area in lack of runoff data is a difficulty in hydrological research. In this article, we try to establish the probability density function of monthly runoff flow by adopting kernal density estimation method, and give the solution by Markov Chain Monte Carlo (MCMC) simulation method based on Adaptive Metropolis (AM) algorithm. Case study shows that the AM-MCMC algorithm model based on kernel density estimation is of high accuracy and good application value. It can be used in areas in lack of data.

runoff simulation; probability distribution; kernel density estimation; AM-MCMC algorithm; Luo’ao Reservoir

2016-08-17;

2016-09-29

南京水利科学研究院院基金项目(Y516011);水利部公益性项目(201201020)

童 坤(1986-)，女，江苏高邮人，工程师，博士，主要从事水资源配置方面的研究工作。E-mail:tongkun0502@hotmail.com

10.11988/ckyyb.20160843

TV214

A

1001-5485(2018)01-0036-04

(编辑：王 慰)