改进恒力矩法测定刚体转动惯量

杨达晓 张家伟 杨耀辉 陈学文 姚雪 谭仁兵

(重庆科技学院数理学院， 重庆 401331)

改进恒力矩法测定刚体转动惯量

杨达晓 张家伟 杨耀辉 陈学文 姚雪 谭仁兵

(重庆科技学院数理学院， 重庆 401331)

针对大学物理专业课中刚体转动惯量的测定问题进行研究。选择合适的砝码及塔轮半径组合，让系统进行一次减速运动和一次加速运动，以测量刚体转动惯量。采用改进恒力矩的测定方法，实验阻力矩随角速度变化对实验结果的影响程度减小，测量结果准确性得到提高，误差减小。

阻力矩； 刚体； 转动惯量； 恒力矩

在大学物理实验课中，常采用落体法测量刚体转动惯量。落体法原理简单，但受测量过程中各种因素的干扰，测量结果精度不高，误差较大。有研究者建议，测量时尽量选择小质量砝码和小半径塔轮[1-2]。也有研究者认为，可通过多次反复实验，筛选合适的数据进行计算。对此问题，研究者提出了多种方法[3-8]。目前尚无方法彻底避免或减小阻力矩随角速度变化的影响，本次研究尝试将改进的恒力矩法用于刚体转动贯量测量。

1 测定刚体转动惯量的原理

刚体作定轴转动时，若所受的合外力矩为M，此时的角加速度为β，该刚体的转动惯量为J，则根据刚体的定轴转动定律有：M=Jβ。此时，只需测出力矩M和角加速度β，则可计算出转动惯量J。

1.1 落体法的原理

在进行实验测量时，所测刚体需要放置在一个实验台上作定轴转动。实验台的转动惯量未知，需要先给空实验台一定初始角速度使其作减速转动，再通过细线将质量为m的砝码绕在半径为r的实验台塔轮上，使砝码下落；系统在恒外力作用下将作加速运动，记录减速、加速转动角位移与时间的关系，并假设转动时系统所受力矩为恒力矩，通过对应公式计算空实验台角加速度和转动惯量。同理，在实验台上放置待测刚体，测出系统的转动惯量。再根据转动惯量的叠加原理，计算待测刚体的转动惯量。

在测量过程中，系统作减速运动时的初始角速度不受限制，随意性较大。已有研究证实，阻力矩随角速度变化，导致多次测量结果不一致，且相对误差偏大。

1.2 改进恒力矩法的原理

为了改变测量过程中系统作减速运动时初始角速度的随意性，对恒力矩法加以改进。图1所示为改进恒力矩法实验台与砝码的运动示意图。

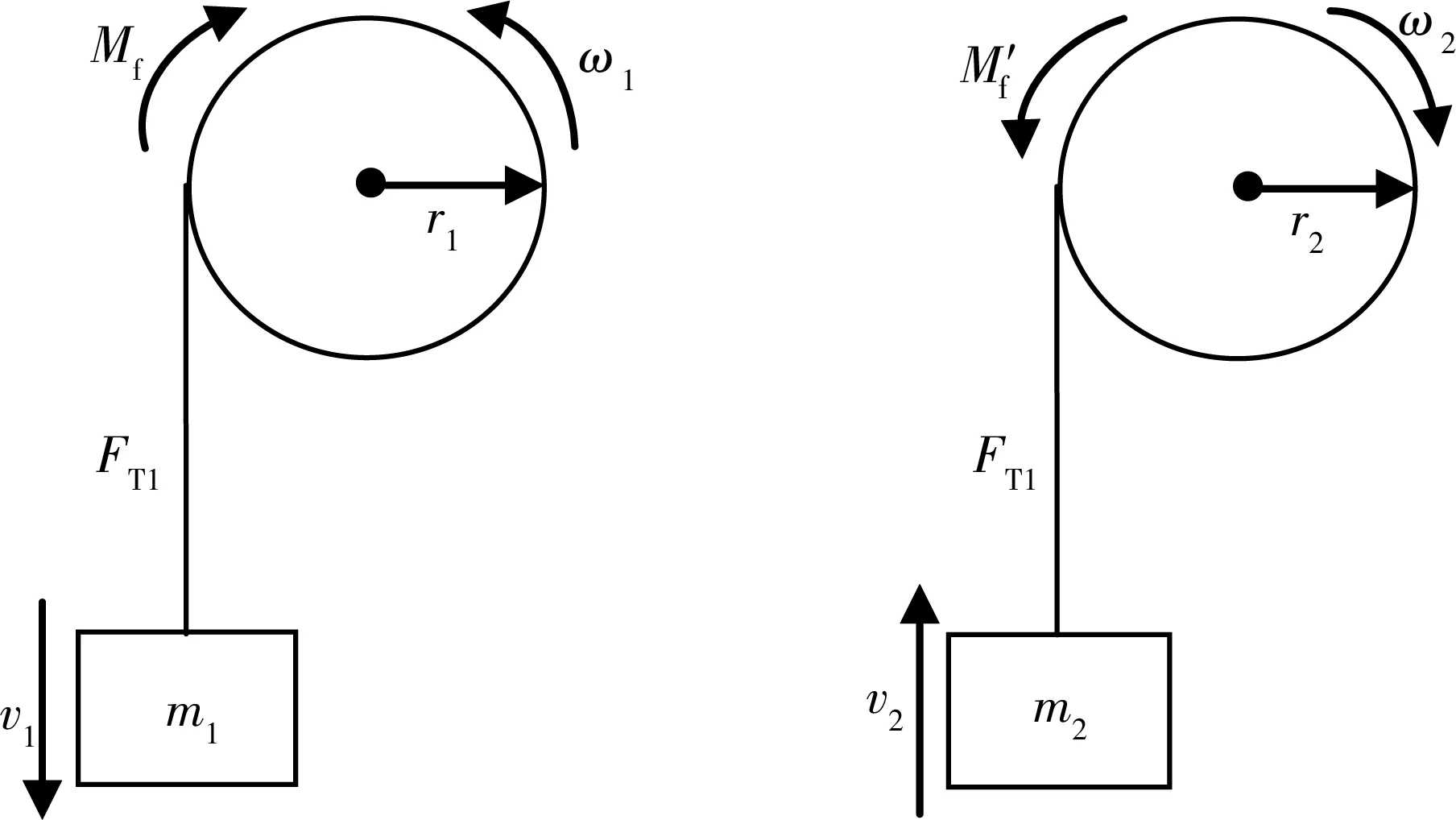
图1 改进恒力矩法实验台与砝码的运动示意图

将质量为m1的砝码用细线绕在半径为r1的塔轮上，使砝码下落，系统在恒外力作用下将作匀加速运动。实验台加速转动时，受阻力矩Mf和拉力矩rFT1的作用，角加速度大小为β1。砝码受重力m1g和绳拉力FT1作用，加速度大小为a1。设实验台转动惯量为J1，忽略滑轮摩擦力矩及质量。根据牛顿第二定律和转动定律，有

m1g-FT1=m1a1=m1r1β1

(1)

r1FT1-Mf=J1β1

(2)

则有

m1r1(g-r1β1)-Mf=J1β1

(3)

再将质量为m2的砝码用细线绕在半径为r2的塔轮上，给实验台一定的初始角速度，使塔轮通过细线带动砝码上升，系统在恒外力作用下将作匀减速运动。有

FT2-m2g=m2a2=m2r2β2

(4)

(5)

(6)

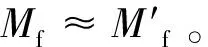
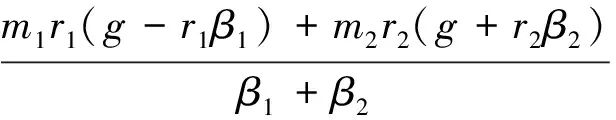
(7)

同理，若实验台放置被测物体后系统的转动惯量为J2，利用对应质量砝码和半径塔轮组合，测出作匀加速和匀减速运动的角加速度大小分别为β3与β4，可得

(8)

以上各式中，β1、β2、β3、β4均取绝对值。根据转动惯量叠加原理，被测物体转动惯量为

J3=J2-J1

(9)

2 利用1次匀加速和1次匀减速转动测量

2.1 实验数据及计算

实验中，使用塔轮半径r为15、20、25 mm，砝码质量分别为34.22、44.59、54.80 g，塔轮半径和砝码质量根据m1gr1和m2gr2大小接近的原则进行组合。圆盘质量为491.46 g，直径为240 mm，转动惯量理论值为0.003 539 kg·m2。

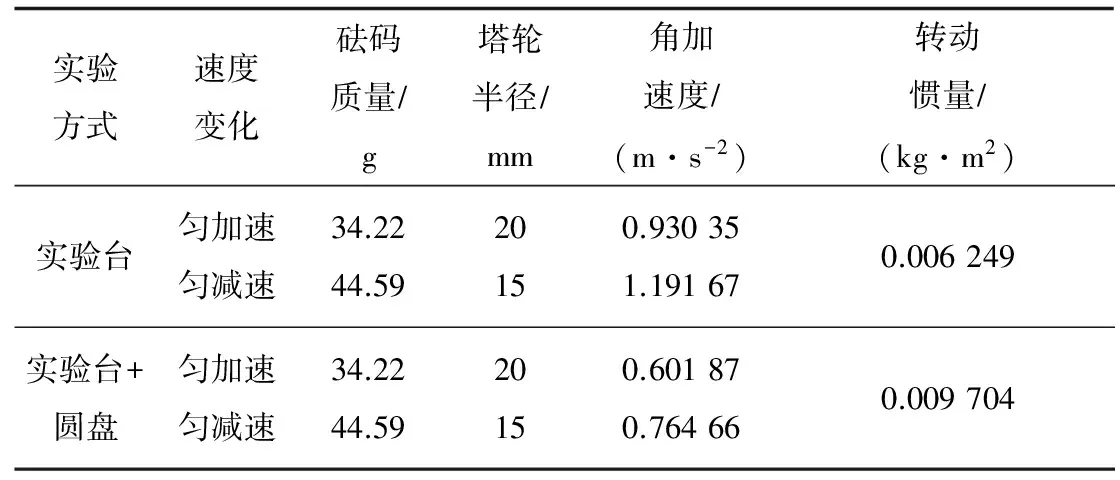
表1 利用匀加速和匀减速转动测量转动惯量(组合一)

注：圆盘转动惯量实验值为0.003 455 kg·m2，相对误差2.36%。

表2 利用匀加速和匀减速转动测量转动惯量(组合二)

注：圆盘转动惯量实验值为0.003 478kg·m2，相对误差1.72%。

表3 利用匀加速和匀减速转动测量转动惯量(组合三)

注：圆盘转动惯量实验值为0.003 416 kg·m2，相对误差3.46%。

表4 利用匀加速和匀减速转动测量转动惯量(组合四)

注：圆盘转动惯量实验值为0.003 452 kg·m2，相对误差2.43%。

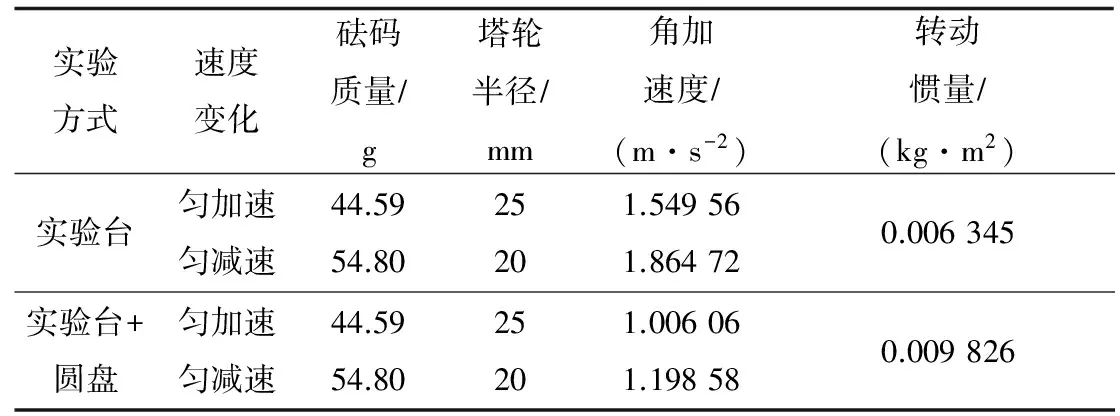
表5 利用匀加速和匀减速转动测量转动惯量(组合五)

注：圆盘转动惯量实验值为0.003 482 kg·m2，相对误差1.61%。

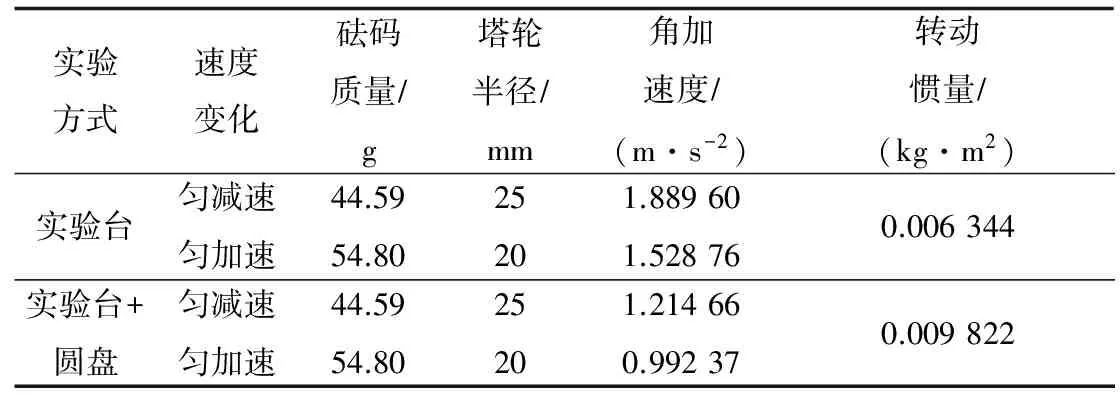
表6 利用匀加速和匀减速转动测量转动惯量(组合六)

注：圆盘转动惯量实验值为0.003 478 kg·m2，相对误差1.70%。

根据式(1)、(3)、(4)、(6)可计算得到测量时组合一对应的阻力矩和拉力矩(见表7)。其他组合阻力矩和拉力矩以此类推。

2.2 结果分析

由表1 — 表6可知，使用不同砝码质量和塔轮半径组合测量时，系统做匀加速和匀减速运动时的角加速度大小略有不同。每次测量过程角速度变化范围、阻力矩大小稍有差别，最终测得圆盘转动惯量实验值和理论值有差别。此外，不同组合中系统做匀加速和匀减速运动时的角加速度大小差异程度不同，角速度变化范围不同，摩擦阻力矩大小虽然会发生变化。但是，系统转动时还会产生细绳拉力矩，由表7可知摩擦阻力矩占系统所受合力矩的比例约为13%，故测量过程中系统所受合力矩变化较小。不同组合所得结果误差大小虽有所差别，但相对误差均较小，为3%左右，符合实验要求。

表7 利用匀加速和匀减速转动测量转动惯量(组合一)

从6种砝码质量和塔轮半径组合的测量结果来看，实验台转动惯量计算结果差别约为1.91%；实验台和圆盘转动惯量计算结果差别约为1.26%；圆盘转动惯量计算结果差别约为1.93%。每种结果差别都较小，说明利用改进恒力矩法测得结果准确性好，解决了实验时阻力矩随角速度变化影响实验结果准确性问题。

3 实验数据重新组合

3.1 利用2次匀加速转动测量

理论上也可以利用2次匀加速运动测量数据计算物体转动惯量，则对应公式需要修改。若计算时β1、β2、β3、β4均取绝对值，则有

(10)

同理，若在实验台放置被测物体后系统的转动惯量为J2，利用对应质量砝码和半径塔轮组合，测出作匀加速和匀减速运动的角加速度大小分别为β3与β4，可得

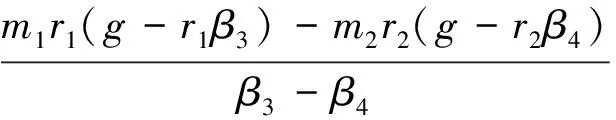
(11)

根据转动惯量叠加原理，被测物体转动惯量为

J3=J2-J1

(12)

利用这种方法，根据所测数据，重新整理数据并计算圆盘转动惯量，结果如表8 — 表10所示。

表8 利用匀加速转动测量转动惯量(组合一)

注：圆盘转动惯量实验值为0.004 523 kg·m2，相对误差27.83%。

3.2 利用2次匀加速测量结果分析

由表8 — 表10可知，利用2次匀加速转动测量数据，使用不同砝码质量和塔轮半径组合测量结果相对误差均较大。实验台转动惯量计算结果最小值为0.006 381 kg·m2，最大值为0.008 370 kg·m2，两者误差为31.2%；实验台和圆盘转动惯量计算结果最小值为0.009 253 kg·m2，最大值为0.012 956 kg·m2，两者误差约为40%；圆盘转动惯量计算结果最小值为0.002 866 kg·m2，最大值为0.004 586 kg·m2，两者误差约为60%。

表9 利用匀加速转动测量转动惯量(组合二)

注：圆盘转动惯量实验值为0.002 866 kg·m2，相对误差19.0%。

表10 利用匀加速转动测量转动惯量(组合三)

注：圆盘转动惯量实验值为0.004 586 kg·m2，相对误差29.6%。

3.3 利用2次匀减速转动测量

当然，理论上也可以利用两次匀减速运动测量计算物体转动惯量，则对应公式需要修改．如计算时β1、β2、β3、β4均取绝对值，有

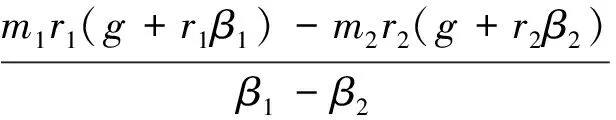
(13)

同理，若在实验台放置被测物体后系统的转动惯量为J2，利用对应质量砝码和半径塔轮组合，测出作匀加速和匀减速运动的角加速度大小分别为β3与β4，可得

(14)

根据转动惯量叠加原理，被测物体转动惯量为

J3=J2-J1

(15)

根据所测数据，重新整理并计算，结果如表11 — 表13所示。

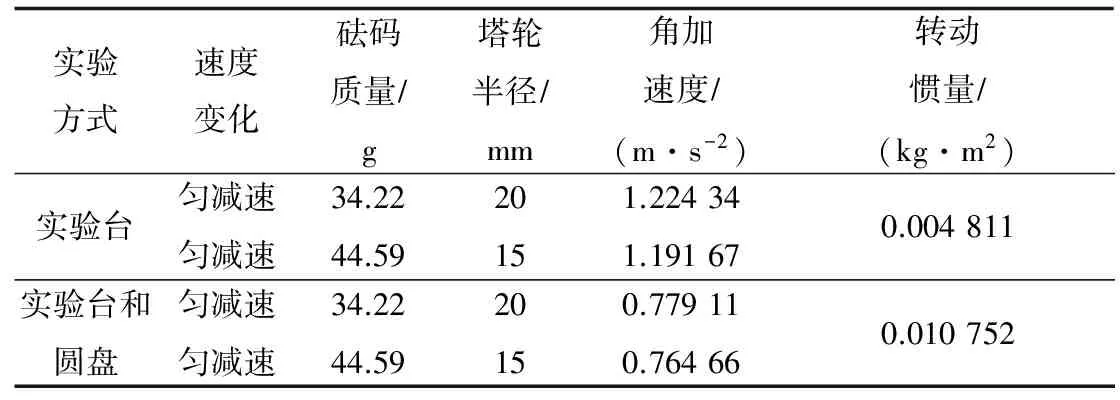
表11 利用匀减速转动测量转动惯量(组合一)

注：圆盘转动惯量实验值为0.005 941 kg·m2，相对误差67.9%。

表12 利用匀减速转动测量转动惯量(组合二)

注：圆盘转动惯量实验值为0.005 215 kg·m2，相对误差47.39%。

表13 利用匀减速转动测量转动惯量(组合三)

注：圆盘转动惯量实验值为0.004 036 kg·m2，相对误差14.06%。

3.4 利用2次匀减速转动测量结果分析

由表11 — 表13可知，利用2次匀减速转动测量数据，使用不同砝码质量和塔轮半径组合测量结果相对误差均较大，说明测量结果也不准确。实验台转动惯量计算结果最小值为0.004 811 kg·m2，最大值为0.007 940 kg·m2，误差约65%；实验台和圆盘转动惯量计算结果最小值为0.010 752 kg·m2，最大值为0.013 155 kg·m2，误差约为22%；圆盘转动惯量计算结果最小值为0.004 036 kg·m2，最大值为0.005 941 kg·m2，误差约为47%。

4 结 语

以上分析结果表明，利用后2种方法测量物体转动惯量，测量结果均不精确，且相对误差大。理论上方法可行，但实际应用效果不好。原因在于，同组数据中两次测量得到的角加速度大小相差较小且有误差，在计算转动惯量时，将2次测量得到的角加速度相减，相减得到的数值为分母。根据误差理论，这种做法结果误差必然很大。

利用改进的恒力矩法进行1次匀加速和1次匀减速转动测量，使用不同质量的砝码和塔轮半径组合，测量物体转动惯量，稳定性和精确度均较好，相对误差较小。这说明改进的恒力矩法能部分解决测量中摩擦阻力矩变化导致的数据不稳定问题。

[1] 班丽瑛.刚体转动惯量实验中影响阻力矩因素研究[J].煤矿机械,2006，27(4)：603-604.

[2] 张艳亮.刚体转动惯量测定实验中阻力矩与角速度关系的研究[J].大学物理实验,2012，25(5)：51-53.

[3] 黄晓清，刘志成，谢鹏,等.刚体转动惯量实验恒力矩测量法数据的稳定性分析[J].中国医学物理学杂志,2016，33(1)：98-102.

[4] 王海林，司嵘嵘，李相银.落体法测量刚体转动惯量实验中引起测量值偏离的因素分析[J].物理实验,2012，32(5)：25-28.

[5] 郭长立，李三庆.落体法测刚体转动惯量的测量方法比较[J].力学与实践,2005，27(3)：69-72.

[6] 庞学霞，邓泽超，李霞,等.恒力矩转动法测刚体转动惯量实验中细线直径的选择[J].实验室科学,2008 (6)：82-83.

[7] 袁树青，范学东，樊林林.用转动惯量仪测刚体的转动惯量误差分析[J].电子测量技术,2013(5)：63-65.

[8] 邓锂强. 刚体转动惯量实验仪实验的误差分析[J]. 实验室科学,2013,16(4): 27-31.

AnImprovedConstantTorqueMethodofMeasuringtheRigidBodyMomentsofInertia

YANGDaxiaoZHANGJiaweiYANGYaohuiCHENXuewenYAOXueTANRenbing

(School of Mathematics and Physics, Chongqing University of Science and Technology, Chongqing 401331, China)

This paper focuses on the study of measurement of rigid body moment of inertia in specialized course of college physics. With the appropriate combination weights and cone radius, the system was carried out a deceleration movement and an acceleration movement, and the rigid body moment of inertia has been measured. With the improved method for measuring constant torque, the impact of variation of resisting moment according to the angular velocity was reduced, and the result was more accurate with smaller error.

resisting moment; rigid body; moment of inertia; constant torque

2017-09-11

国家自然科学基金项目“重味强子的产生和衰变及其新物理效应研究”(11347024)；重庆市科委基金项目“对撞机上重味强子产生和衰变机制的研究”(2014JCYJA00030)；重庆市教委基金项目“重味粒子产生和衰变机制的系统研究”(KJ1401313)；重庆科技学院重点培育基金项目“高亮度正负电子对撞机上重味粒子的研究”(CK2016Z03)

杨达晓(1981 — )，男，硕士，讲师，研究方向为大学物理实验教学。

O313

A

1673-1980(2017)06-0103-05