基于D数的烟花爆竹生产经营企业安全评估

莫泓铭 胡敏 夏龄

(1. 四川民族学院图书馆， 四川 康定 626001； 2. 四川省计算机研究院， 成都 610041；3. 四川民族学院网络信息中心, 四川 康定 626001)

基于D数的烟花爆竹生产经营企业安全评估

莫泓铭1胡敏2夏龄3

(1. 四川民族学院图书馆， 四川 康定 626001； 2. 四川省计算机研究院， 成都 610041；3. 四川民族学院网络信息中心, 四川 康定 626001)

针对烟花爆竹生产经营企业安全评估的问题，建立了基于D数的决策评估模型。该模型充分利用了D数在信息融合、多准则决策方面的优势，可快速系统地实现烟花爆竹生产经营企业的安全性评估。

D数； 证据理论； 安全评估； 烟花爆竹； 企业

一直以来，我国的烟花爆竹行业发展繁荣，缓解了就业压力，也取得了显著的经济效益。然而，烟花爆竹属于易燃易爆产品，在生产中安全事故时发生，往往造成人员伤亡，损失惨重[1]。因此，必须建立合理的安全评估体系，加强烟花爆竹生产经营环节监管，以促进烟花爆竹行业更加安全可靠地发展。

针对烟花爆竹企业的安全性评价问题，研究者提出了安全检查表法、事故树分析法、层次分析法等方法。证据理论作为一种常用的不确定信息表达、融合工具，可应用于烟花爆竹生产经营企业的安全评估。然而，证据理论在实际运用中存在一定的局限性，如一票否决导致违背意愿的结果、各元素之间彼此要相互完全独立、辨识框架要完备等。邓勇教授基于证据理论框架提出了D数理论，该理论完美地解决了证据理论中的这些限制与不足[2]。D数作为一种新的不确定信息表达和处理工具，允许元素间相互不独立的情况存在，同时对于每个元素的信任程度之和可以小于1。D数理论在处理不确定、不完备信息方面具有一定优势，目前已应用于桥梁评估[3]、环境评估[4]、供应商选择[5]、帷幕灌浆效率评估[6]等领域[7-11]。

烟花爆竹生产经营中涉及的安全因素很多，各指标评价体系复杂，且各指标之间可能存在错综复杂的关系。本次研究将建立一套基于D数的烟花爆竹生产经营企业安全评估模型。该模型充分利用了D数表示定性、定量等信息的灵活性，同时运用D数的聚集属性多层次、有步骤地系统化地聚合相关信息，最终得到综合评分，从而完成烟花爆竹生产经营企业的安全评估。

1 证据理论和D数理论

1.1 证据理论

证据理论(evidence theory)是由Dempster于1967年提出，并在1976年由其学生Shafer加以完善推广的一套理论，用于处理不确定信息[12-13]。证据理论不同于传统的贝叶斯概率论，它不需要先验信息，并且将传统概率的单子集赋值拓展到了单子集的幂集空间。由于其强大的信息融合能力，因而广泛用于目标识别、模式识别、故障诊断、风险评估和多属性决策等领域。证据理论的定义如下:

假设，Θ={θ1，θ2，θ3，…，θn}是一个有限的非空互斥集合，证据理论中的辨识框架由该集合的所有子集构成，即Ω={Ø，θ1，θ2，…，θi，…，θn，{θ1，θ2}，{θ1,θ3}，…，Θ}。该框架上的基本概率指派函数(basic probability assignment, BPA)满足以下条件:

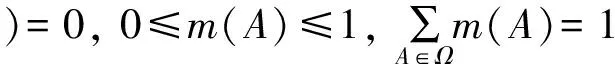
式中：Ø为空集；A为集合Ω的任意子集。

Dempster组合规则是证据理论中的一个重要组成部分，它能够将两个原始的BPA融合并生成一个新的BPA。Dempster组合规则，或称为两个BPA的正交和规则。Dempster组合规则如下：

m(A)=(m1⊕m2)(A)

(1)

(2)

式中，k为冲突系数，反映2个BPA的相容程度。当k=0时，意味着2个BPA是完全一样的。当k=1时，表示2个BPA是完全冲突的，即彼此互相矛盾，Dempster组合规则不适用于此类情形。Dempster组合规则满足交换律和结合律，即：

Ⅰm1⊕m2=m2⊕m1

Ⅱ (m1⊕m2)⊕m3=m1⊕(m2⊕m3)

因此，当存在多个BPA需要融合时，可以不用考虑其先后顺序而逐对进行融合。

1.2 D数理论

D数理论作为证据理论的扩展，克服了证据理论在实际运用中的一些限制与不足[2]，其定义如下：

假设Ω为非空有限集合，D数是一个映射，即D∶Ω→[0，1]，满足以下条件：

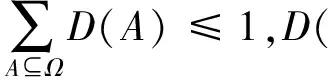
假如Ω={d1，d2，…，di…，dn}，一种特殊形式的D数可以表现为

D(d1)=v1…D(di)=vi…D(dn)=vn

它也可以经简化后表达为：D={(d1，v1)，…，(di，vi)，…，(dn，dn)}。

与证据理论类似，D数也具有以下相应属性。

属性1：交换不变性。假如存在2个D数，D1={(d1，v1)，…，(di，vi)，…，(dn，vn)}，D2={(dn，vn)，…，(di，vi)，…，(d1，v1)}，那么D1和D2被认为是完全相同的。

例1：假设有2个数，D1={(优，0.3)，(良，0.2)}，D2={(良，0.2)，(优，0.3)}，则D1和D2是完全相同的。在本例中，D1和D2的信任度之和均为0.5，小于1，说明这两个D数都是不完备的。

例2：假设有2个数，D1={(1，0.3)，(2，0.2)，(3，0.5)}，D2={(2，0.2)，(3，0.5)，(1，0.3)}，则D1和D2是完全相同的。本例中，D1和D2的信任度之和均为1，说明这2个D数是完备的。

例3：假设在证据理论的同一辨识框架上有2个BPA，B1={(a，0.3)，(b，0.1)，(c，0.6)}，B2={(b，0.1)，(a，0.3)，(c，0.6)}，那么B1和B2是完全相同的。

从上述3个例子可以看出，D数的交换不变性属性在证据理论中也同样适用。

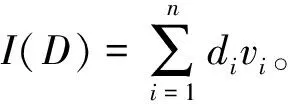
例4：假设一个D数，D={(1，0.5)，(2，0.1)，(3，0.2)，(4，0.2)}，那么I(D)=1×0.5+2×0.1+3×0.2+4×0.2=0.5+0.2+0.6+0.8=2.1。

例5：假设一个D数，D={(3，0.5)，(4，0.1)}，那么I(D)=3×0.5+4×0.1=1.9。

需要说明的是，聚集属性仅适用于特殊的离散的D数。在决策评估中，合理利用D数的聚集属性将大大简化和加快决策评估过程。

2 基于D数的决策评估模型

D数理论提供了一种比证据理论更为灵活的信息表达方式。在D数理论的实际运用中，允许专家根据自身经验、知识等实际情况表达自己的观点，而不必拘泥于观点信任度分配的完备性。D数的聚集属性提供了一种新的层次化、系统化的信息融合方式。在此，我们将构建基于D数的多准则属性评估模型，该模型通过引入评价指标体系、权重等供专家评分参考，专家的观点以D数的方式来表现，运用D数的聚集属性以多层次、递归的方式不断融合相关决策评价信息，最终得到总体评价结果。图1所示为基于D数的决策评估模型流程。

Step 1 每一个对象都不是孤立的，都可以从多角度、多指标出发进行评估。分析待评估对象，选择合理的指标评价体系。

Step 2 选定待评价的指标后，结合评估的侧重点，合理给定权重，或引入第三方评估各指标的权重。

Step 3 提供相关的安全评价标准及其对应的评价值，供专家在评估时选用。安全评价标准即构成D数的辨识框架。

Step 4 专家根据自身经验和知识情况，结合提供的安全评价标准，在充分调研的基础上进行打分、评价。

Step 5 运行D数的聚集属性，分步骤地集成专家对各指标体系的评分结果。

Step 6 根据融合结果，对照安全评价标准的评价值，最终确定评价等级。

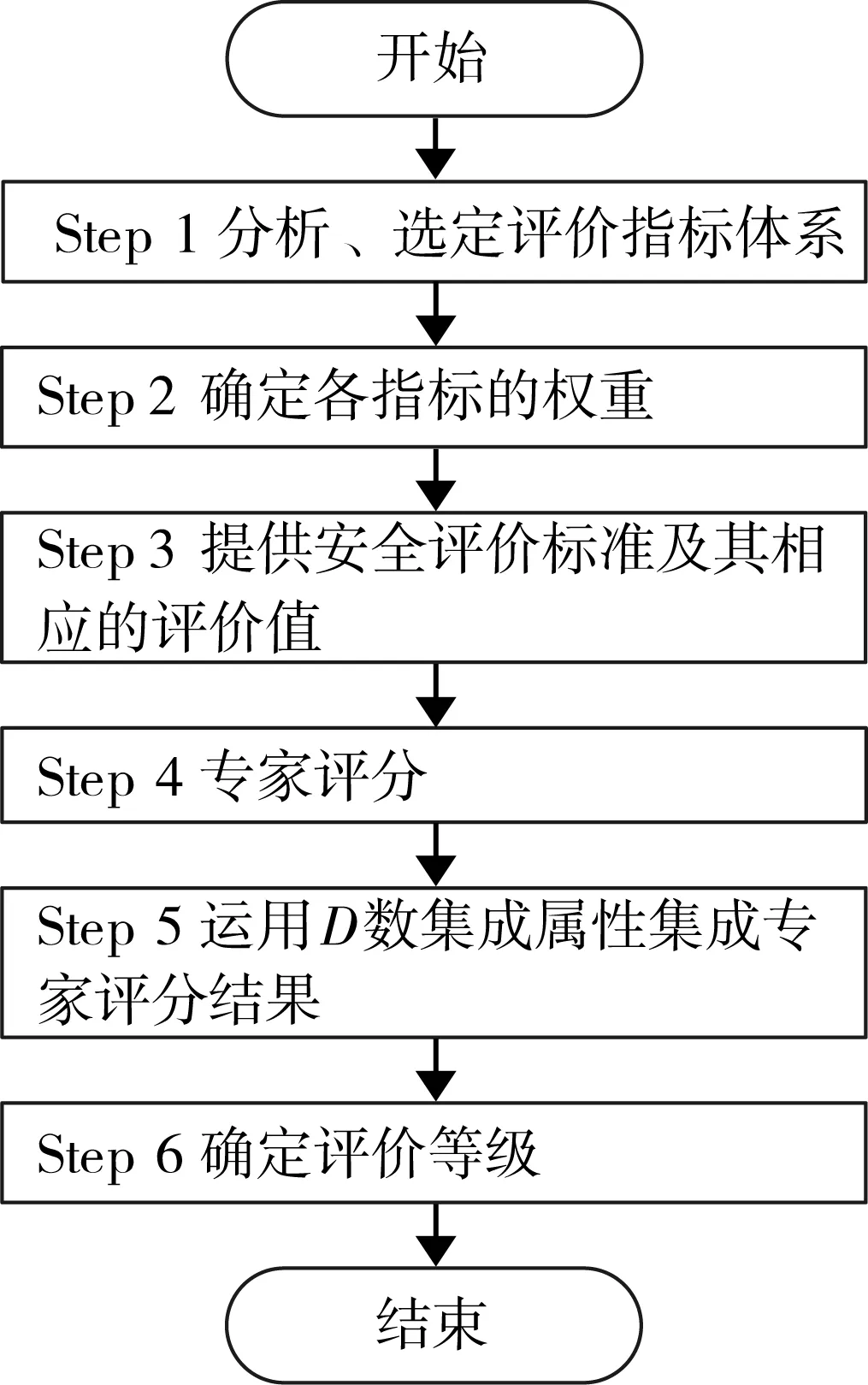
图1 基于D数的决策评估模型流程

3 实例应用

某地拟新建烟花爆炸生产经营企业，该企业向相关部门申请相关安全营业执照许可证。相关部门在收到该企业的申请后，立即组织专家对该企业的安全性进行评估。在评估时，专家采用了基于D数的决策评估模型。其实际评估过程如下：

Step 1 由于烟花爆竹生产经营所涉及到的风险指标较多，选择评价指标时应遵循实用性、可测性、科学性、层次性等原则。在实施评估决策前，应首先对其进行充分分析再选择合适的评价指标[14]。烟花爆竹生产经营系统风险指标体系分为2层结构：第一层为一级指标(模块化)，包括生产储运过程因素指标C1，生产储运条件因素指标C2，安全管理因素指标C3；第二层为由一级指标细化、分解后的二级指标。图2所示为烟花爆竹生产经营系统风险评价指标体系。

Step 2 采用专家打分法确定各指标的权重[14-15]，如表1所示。

Step 3 为专家提供以下模糊评价集[16]作为评估参考，P={P1(差)，P2(较差)，P3(一般)，P4(较好)，P5(好)}，并给出对应的模糊评价值S(P)={0.2，0.4，0.6，0.8，1.0}。

Step 4 组织专家进行评分，评分的原始数据如表2所示。

图2 烟花爆竹生产经营系统风险评价指标体系

表1 烟花爆竹生产经营系统风险评价指标及其权重

表2 专家组决策评分表

Step 5 运用D数的聚集属性，分步融合专家评分信息及相关指标权重，即

(3)

其中，I(Ci)为第i个一级指标的D数聚集值，Wi为第i个一级指标的权重。第i个一级指标Ci的D数聚集值又由其下的j个二级指标Cij分别与其对应的权重Wij之积的和所构成，即

(4)

其中，Cij为第i个一级指标下的第j个二级指标，Wij为第i个一级指标下的第j个二级指标的权重。

(5)

其中，Pk为系统提供的等级评价，Mijk为专家组针对二级指标Cij做出等级为Pk的评分。

接下来，以生产储运过程指标C1为例，演示其基于D数的决策实施过程。

由表1可知，一级指标C1由C11、C12、C13、C14、C15、C16等6个二级指标构成，即q=6。由公式(4)计算一级指标C1的D数聚集值：

其中，I(C1j)的D数聚集值可由相应的评价等级与分数的乘积获得。

以二级指标C11为例，据公式(5)得：

一共产生5个评价等级，即y=5。结合模糊评价，有：

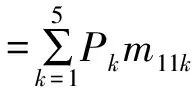
=P1×M111+P2×M112+P3×M113+

P4×M114+P5×M115

=0.2×0+0.4×0+0.6×0.2+

0.8×0.5+1×0.3

=0.82

同理，一级指标C1下的其他二级指标有：

I(C12)=0.82I(C13)=0.84I(C14)=0.86I(C15)=0.80I(C16)=0.80

所以，一级指标C1的D数聚集值有：

=0.82×0.114+0.82×0.204+

0.84×0.176+0.86×0.262+

0.80×0.140+0.80×0.104

=0.829 1

类似地，其他一级指标的D数聚集值有：

I(C2)=0.827 9I(C3)=0.842 5

烟花爆竹生产经营企业安全评价体系由3个一级指标构成，即n=3。据公式(3)，得出下式：

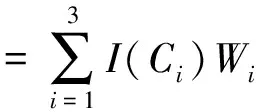
=0.829 1×0.3+0.827 9×0.3+

0.842 5×0.4

=0.834 1

Step 6 该企业安全评价的最终D数评价值为0.834 1。结合模糊评价值及模糊评价集，0.8<0.843 1<1，于是，认定该企业安全评估处于较安全水平。

为验证本决策评估模型的有效性，采用与文献[15]所提出的基于证据理论的方法评估本实例。文献[15]通过证据信度分配及合成的方法得到的结果为较安全，与本次建立模型得到的结果一致。但相较而言，本模型充分利用了D数的聚集属性，模型流程直观，层次清楚，可操作性强。

4 结 语

通过对D数概念及其相关属性的介绍，建立了基于D数的决策评估模型，给出了具体的步骤与实例分析。D数作为一种不确定信息的新表达方法，弥补了证据理论的一些固有缺陷，能更加灵活有效地处理与表达不确定信息。相关研究表明，烟花爆竹生产中，易燃易爆物质多，易发生事故的工艺多，爆炸与燃烧交互进行，爆炸与燃烧的产物有毒有害，人员伤亡率高，必须进行相应的安全性评估。将烟花爆竹生产经营企业所涉及到的安全性指标进行两级分解，分别赋予其不同的权重，组织专家评分评判，通过不断融合专家对各指标的评价，最后得到综合评价。实例验证表明，本模型的操作性强，简单有效，具有实用价值。值得一提的是，相对于基于证据理论的评估模型而言，基于D数的决策评估模型应用范围更广泛，在信息不完备的情况下仍然能有效地融合信息。本次所建决策评估模型具有广泛的拓展性与普适性。

[1] 李秀琴. 烟花爆竹安全与管理[M]. 北京: 化学工业出版社, 2007：10-20.

[2] DENG Y.Dnumbers: theory and applications[J]. Journal of Information and Computational Science, 2012, 9(9): 2421-2428.

[3] DENG X Y，HU Y，DENG Y. Bridge condition assessment using d Numbers[J]. The Scientific World Journal, 2014, 2014: 571-578.

[4] DENG X Y，HU Y，DENG Y，et al. Environmental impact assessment based on d numbers[J]. Expert Systems with Applications, 2014, 41(2): 635-643.

[5] DENG X Y，HU Y，DENG Y，et al. Supplier selection using AHP methodology extended byDnumbers[J]. Expert Systems with Applications, 2014, 41(1): 156-167.

[6] FAN G C，ZHONG D H，YAN F G，et al. A hybrid fuzzy evaluation method for curtain grouting efficiency assessment based on an AHP method extended by d numbers[J]. Expert Systems with Applications, 2016, 44: 289-303.

[7] LIU H C，YOU J X，FAN X J，et al. Failure mode and effects analysis using d numbers and grey relational projection method[J]. Expert Systems with Applications, 2014, 41(10): 4670-4679.

[8] XINYANG DENG，XI LU，FELIX T S C，et al. D-CFPR:Dnumbers extended consistent fuzzy preference relations[J]. Knowledge-Based Systems, 2015, 73: 61-68.

[9] 王宁奎，魏代俊. 基于D数理论的不确定多属性决策方法[J]. 湖北民族学院学报 (自然科学版), 2016, 34(1): 35-39.

[10] ZHOU X Y，DENG X Y，DENG Y，et al. Dependence assessment in human reliability analysis based onDnumbers and AHP[J]. Nuclear Engineering and Design, 2017, 313: 243-252.

[11] 王坚强，黄思旷. 基于模糊熵和证据推理的语言D数多准则决策方法[J]. 控制与决策, 2016, 31(4): 673-677.

[12] DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. The annals of mathematical statistics, 1967, 38(2): 325-339.

[13] SHAFER G. A mathematical theory of evidence[M]. Princeton：Princeton University Press, 1976：10-20.

[14] 王兆国. 烟花爆竹生产经营企业安全标准化规范探讨[D]. 太原：中北大学, 2010：10-20.

[15] 甄超英，董龙洋，鲁文浩. 基于证据理论的烟花爆竹生产经营企业安全评价方法研究[J]. 安全与环境工程, 2012, 19(2): 84-87.

[16] 丁松滨，石荣，施和平. 证据理论在空中交通管理安全评价中的应用[J]. 中国民航学院学报，2006, 24(6): 38-41.

SafetyAssessmentforFireworksandFirecrackersProductionandManagementEnterprisesbasedonDnumbers

MOHongming1HUMin2XIALing3

(1.Library of Sichuan Minzu College, Kangding Sichuang 626001, China; 2.Sichuan Institute of Computer Sciences, Chengdu 610041, China; 3.Network Center of Sichuan Minzu College, Kangding Sichuan 626001, China)

In order to assess the safety of fireworks and firecrackers enterprises, a model of security evaluation is built based onDnumbers. The proposed model takes advantage ofDnumbers in information fusion and multi-criteria decision-making to evaluate the safety for fireworks and firecrackers enterprises quickly and systematically.

Dnumbers; evidence theory; safety assessment; fireworks and firecrackers; enterprise

2017-06-07

四川省教育厅2017年自然科学科研项目“基于信度函数的复杂网络节点重要性评价研究”(17ZB0328)

莫泓铭(1983 — )，男，助理研究员，研究方向为多源信息融合、安全评估、多属性决策等。

X932

A

1673-1980(2017)06-0086-05