考虑井间干扰影响的底水油藏见水时间公式改进
史建国 乐平 周建堂 汤连东 付玉 谢志伟
(1. 长庆油田第四采油厂, 陕西 榆林 719000; 2. 西南石油大学石油与天然气工程学院, 成都 610500)
考虑井间干扰影响的底水油藏见水时间公式改进
史建国1乐平2周建堂1汤连东2付玉2谢志伟2
(1. 长庆油田第四采油厂, 陕西 榆林 719000; 2. 西南石油大学石油与天然气工程学院, 成都 610500)
在井距较小的底水油藏中,井间干扰现象往往影响油井见水时间预测结果的准确性。根据势函数叠加原理,提出考虑井间干扰影响的底水油藏油井见水时间预测方法,探讨井间距离和邻井产量等参数对油井见水时间的影响。计算结果表明,如果井间距离越小、油井产量越大,则井间干扰越大、油井见水时间越早;邻井产量和井距对油井见水时间的影响程度随着井距的增大而减小。
底水油藏; 井间干扰; 见水时间
事先预报油井的见水时间,是底水油藏开发管理工作的任务之一。准确预测底水油藏油井的见水时间,是开采透底水油藏的关键问题之一。本次研究中,基于相关研究成果[1-10],运用势的叠加原理探讨井间干扰现象对底水油藏油井见水时间的影响,对李传亮推导的油井见水时间公式进行了改进。
1 井间干扰现象
通常在研究某问题时,往往假设在圆形地层中心仅有一口生产井,而实践中却是有大批井同时钻探,有些大油田甚至有上千口生产井同时钻探,这些井工作时相互之间会产生一定干扰,这种干扰称为井间干扰。井间干扰通常会导致相邻生产井的压力发生变化[11-12]。图1所示为两口生产井间干扰压力分布曲线。
假设地层中有生产井A井和B井。当两井单独生产时,消耗的地层能量形成图1中实线所示压降漏斗。但实践中,两井往往是同时以原产量水平进行生产,地层原来消耗的能量并不能维持两井的产量水平。此时,为了保持两井产量不变,消耗的地层能量应形成图1中虚线所示压降漏斗。
井间干扰的实质是地层能量的重新平衡。能量的大小通过压力表示,故井间干扰的最终结果表现为地层中压力的重新分布。这种重新分布是按照压降叠加原理进行的,即多井同时工作时,地层内各点的压降等于各井单独工作时的压降代数和。
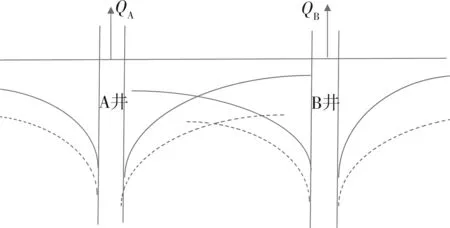
图1 两口生产井间干扰压力分布曲线
2 模型的建立及公式推导
2.1 模型的建立
某无隔板底水油藏有A井和B井(见图1),A井为中心井,B井为偏心井,油层厚度为h。原始油水边界近似为水平面,底水距井底距离为ho,两井间距为R。当油井开始投产后,底水开始向井底锥进(见图2)。模型的假设条件如下:(1)该油层为均质地层,流体在油层中稳定流动; (2)水驱油过程中未发现任何化学物理反应;(3)忽略毛管力、重力和表皮因子的影响,油水的密度和黏度均为常数;(4)油藏供给边界上的压力保持恒定。
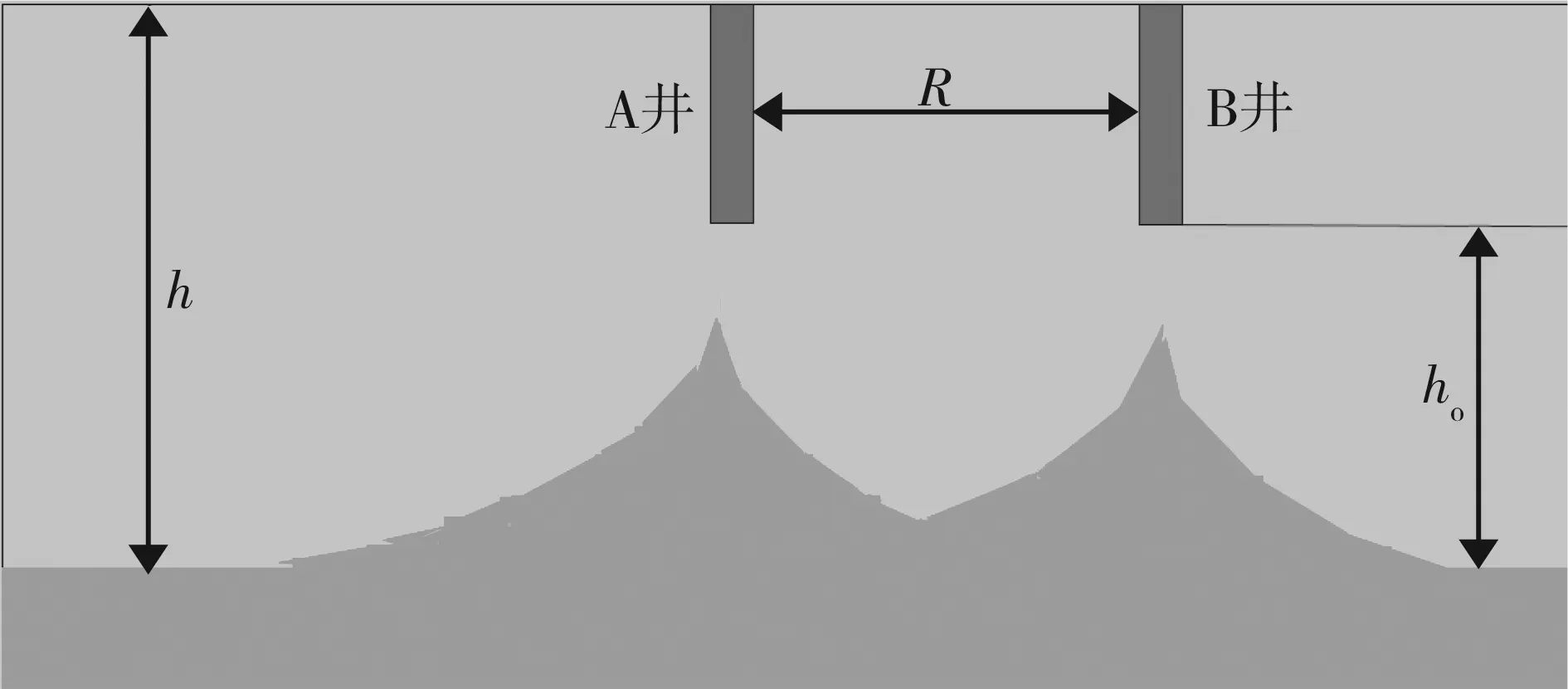
图2 板底水油藏底水锥进示意图
2.2 公式推导
根据地层的井间距离和边界条件,将A井、B井的干扰分为无井间干扰和有井间干扰两种情况。
(1) 无井间干扰。地层中A井、B井同时生产且井距R>Re,或仅单井生产。此时,不考虑井间干扰的影响,油井见水时间均相同[11]。
A井为中心井,其见水时间计算公式如下:
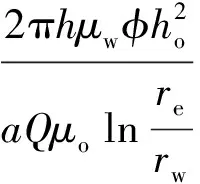
(1)
式中:t—— 见水时间,h;
h—— 油层厚度, m;
ho—— 底水到井底的距离,m;
μw—— 水的黏度,mPa·s;
μo—— 油的黏度,mPa·s;
a—— 储集层垂向渗透率与水平渗透率之比;
φ—— 储集层的孔隙度;
re—— 泄油半径,m;
rw—— 井筒半径,m;
Q—— 油井的总产量, m3d。
B井为偏心井,其见水时间计算公式如下:

(2)
式中:R—— 偏心距,m。
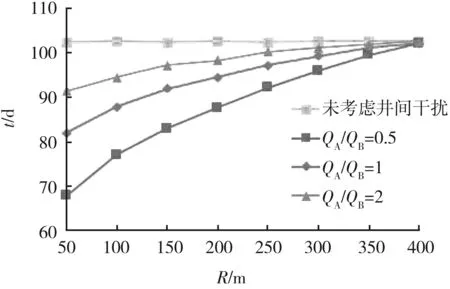
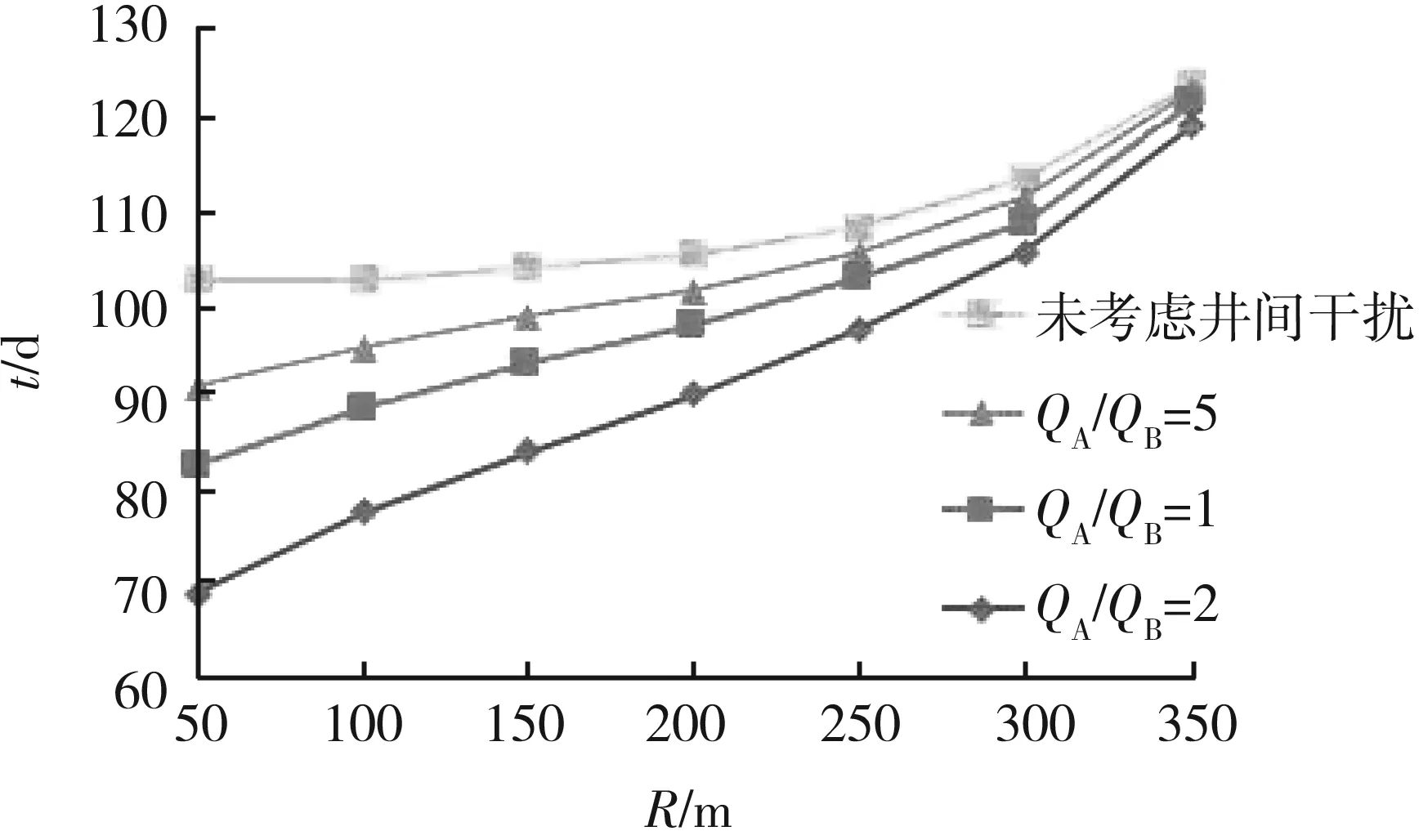
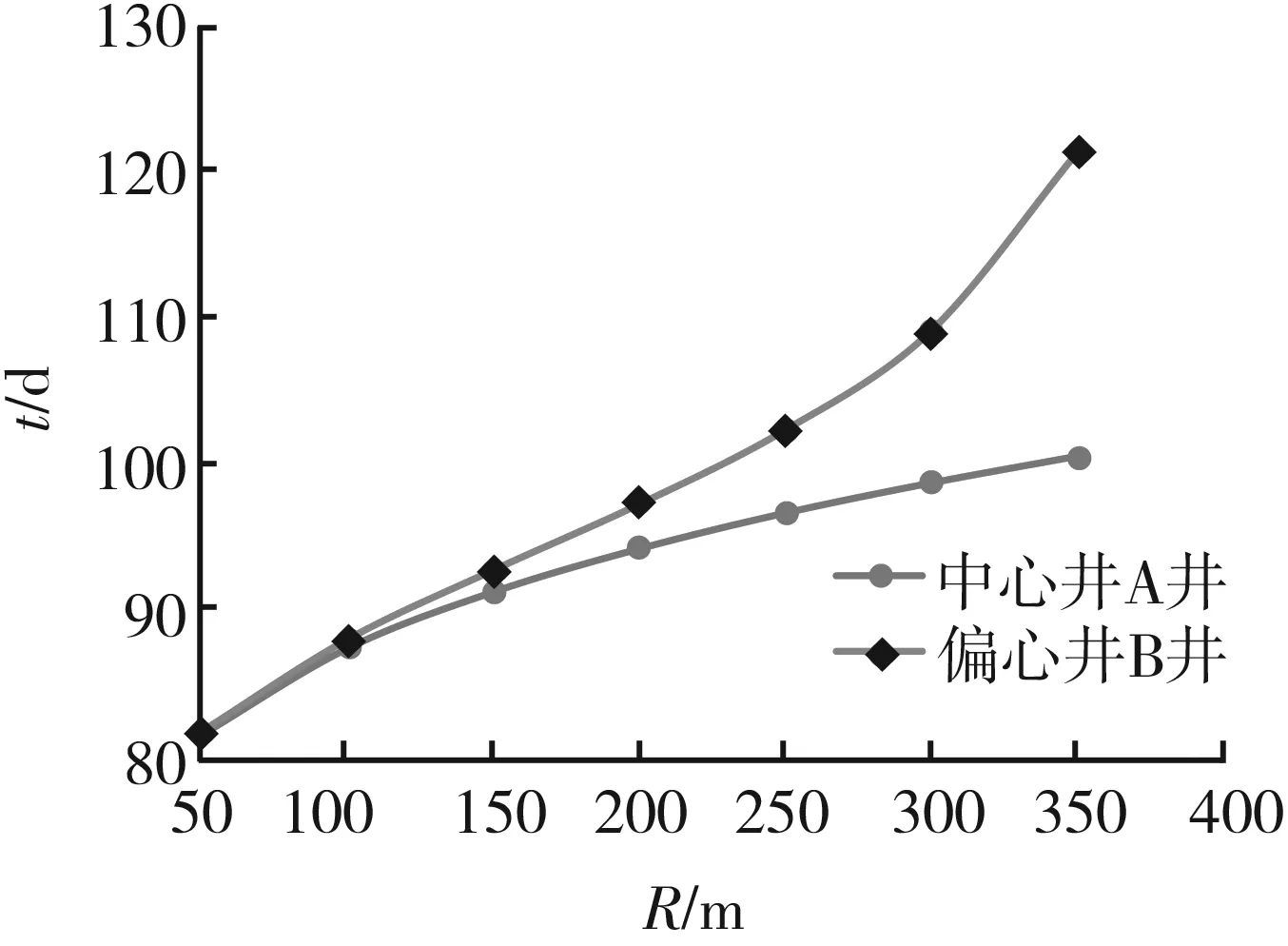
(2) 有井间干扰。当地层中A井、B井的井距为0 A井、B井的产量分别为QA、QB,计算地层平面上任意一点M处的势: (3) 式中:Φ—— 距井半径r处地层的势; r—— 地层中任意一点到井的距离,m; C—— 常数,与边界条件有关; q—— 单位地层厚度的产量。 单位地层厚度的产量为: (4) 根据达西定律计算地层的势: (5) 当A井、B井同时工作时,对于中心井A而言存在以下关系。 地层中供给边缘re处的势Φe为: (6) 油井A井壁边界rw处的势Φw为: (7) 式(6)、(7)相减可得: (8) (9) 式中:pe—— 地层压力,MPa; pw—— 井底流压,MPa。 根据势叠加原理,推导出偏心井B井的井底压降: (10) 李传亮提出的油井见水时间公式为: (11) 该公式并未考虑井间干扰的影响。本次研究将在该公式的基础上加以改进,分析井间干扰现象对底水油藏油井时间的影响。 得到考虑井间干扰的中心井A井见水时间预测改进公式: (12) 偏心油井B井见水时间预测改进公式: (13) 式中:QB—— 偏心井B井产量,m3d; QA—— 中心井A井产量,m3d。 若中心井A井附近有n口偏心井同时生产,根据压降叠加原则,地层中任一点的压降等于毎口井单独工作时该点所产生压降的代数和,得到其数学表达式: Δpn=pe-pn (14) 中心井A井的井底压降为: (15) 此时得到考虑井间干扰的中心油井A井见水时间预测公式为: (16) 以某底水渗透油藏实际相邻的A井、B井为例,研究井间干扰对油井见水时间的影响。A井为中心井,B井为偏心井,计算A、B井的见水时间。油井相关参数如下:油层厚度为30 m;油井打开厚度为15 m;泄油半径为400 m;渗透率为1 500×10-3μm2;井距r处地层的势为0.3;储集层垂向渗透率与水平渗透率之比为0.1;井筒半径为0.1 m;井距R为150 m;原油黏度为5 mPa·s;地层水黏度为0.8 mPa·s;油井产量分别取12、24、48 m3d;井间距分别取50、100、150、200、250、300、350 m。 中心井A井以定产量QA进行生产,改变偏心井到中心井井距R和产量QB,分析两井井距R和偏心井产量QB对中心井见水时间的影响。由图3可知,在考虑井间干扰条件下,中心井见水时间比未考虑井间干扰的见水时间更早。偏心井以相同产量进行生产时, 中心井见水时间随着两井井距的增大而延迟。两井井距R越大,考虑井间干扰与未考虑井间干扰的中心井见水时间误差越小。在相同井距条件下,偏心井的产量越大,中心井见水时间越早。在实际现场中,为了防止底水锥进过快,应该确定合理的两井井距和产量,预测见水时间时必须考虑井间干扰的影响。 图3 中心井A见水时间曲线图 偏心井B井以定产量QB进行生产,改变偏心井到中心井井距R和产量QA,分析两井井距R和中心井产量QA对偏心井见水时间的影响。由图4可知,在考虑井间干扰的情况下,偏心井见水时间比未考虑井间干扰的见水时间更早。中心井以相同产量生产时,偏心井见水时间随着两井井距的增大而变大。两井井距R越大,考虑井间干扰的偏心井见水时间与未考虑井间干扰的偏心井见水时间之间误差越小。在相同井距条件下,中心井的产量越大,偏心井见水越早。 图4 偏心井B见水时间曲线图 在考虑井间干扰的条件下,中心井与偏心井以相同产量进行生产,两井见水时间的关系如图5所示。当两井井距小于150 m时,两井见水时间差相对较小。但随着井距不断增加,中心井与偏心井见水时间差越来越大。偏心井见水时间比中心井更晚。在现场条件下预测油井见水时间时,应分清中心井与偏心井,二者不能采用同一方法来预测,否则预测结果误差较大。 图5 中心井A井与偏心井B井见水关系曲线 本次研究中,基于势叠加原理提出了新的底水油藏见水时间预测模型,推导出考虑井间干扰的底水油藏预测公式,更加符合现场实际情况。为了延缓底水锥进,推迟油井见水时间,应合理确定井间距离和生产产量。井间距离越小、生产产量越大,则井间干扰越大、油井见水时间越早。邻井产量和两井井距对油井见水时间的影响程度随着井距的增加而减小。预测油井见水时间,应区分中心井与偏心井。 当井距较大时,偏心井见水时间比中心井见水时间更晚。两井不能采用同一方法预测,否则预测结果误差较大。 [1] 韦建伟, 罗锋, 唐人选. 关于开采底水油藏几个重要参数的确定[J]. 大庆石油地质与开发, 2003, 22(5):25-27. [2] 唐人选. 底水油藏水锥动态模拟及见水时间预测[J]. 新疆石油地质, 2003, 24(6):572-573. [3] 李传亮. 半渗透隔板底水油藏油井见水时间预报公式[J]. 大庆石油地质与开发, 2001, 20(4):32-33. [4] 朱圣举. 预测无隔板底水油藏油井见水时间的修正式[J]. 新疆石油地质, 1999(1):56-57. [5] 刘彦成, 王健, 戢磊,等. 无隔板底水油藏中堵剂位置的确定[J]. 新疆石油地质, 2010, 31(2):186-187. [6] 熊小伟, 李云鹏, 张静蕾,等. 一种预测底水油藏水锥动态及见水时间的新方法[J]. 断块油气田, 2014, 21(2):221-223. [7] 刘昱, 魏宏让. 缝洞型底水油藏见水时间预测方法研究[J]. 内蒙古石油化工, 2010, 36(3):13-14. [8] 郭秀文. 边底水油藏见水时间及无水期采收率的确定[J]. 断块油气田, 2003, 10(1):51-52. [9] 时宇, 杨正明, 张训华. 气顶底水油藏水平井井间干扰研究[J]. 大庆石油地质与开发, 2008, 27(5):62-66. [10] 范子菲, 傅秀娟. 气顶底水油藏水平井锥进的油藏工程研究[J]. 大庆石油地质与开发, 1995(3):38-43. [11] 李传亮. 油藏工程原理[M]. 北京:石油工业出版社, 2011:363-365. [12] 张建国. 油气层渗流力学[M]. 北京:中国石油大学出版社, 2010:77-83. FormulaofWaterBreakthroughTimeofBottomWaterReservoirConsideringWellInterference SHIJianguo1YUEPing2ZHOUJiantang1TANGLiandong2FUYu2XIEZhiwei2 (1.The Fourth Oil Extraction Plant in Changqing Oilfield, Yulin Shaanxi 719000, China;2.College of Petroleum and Natural Gas Engineering, Southwest Petroleum University, Chengdu 610500, China) The interwell interference often affects the accuracy of the prediction results of water breakthrough time in a bottom water reservoir with smaller well spacing. Based on superposition principle of potential function, a new prediction formula considering the phenomenon of well interference is set up to explore the effects of the distance between adjacent wells and oil well production on water breakthrough time. The results show that smaller distance and greater oil well production would cause bigger interference and earlier water breakthrough time. The influence of the output and well spacing of the well on the water breakthrough time of the well decreases with the increase of the well spacing. bottom water reservoir; well interference; water breakthrough time 2017-06-06 国家自然科学基金青年科学基金项目“考虑启动条件和井筒压降的底水油藏分支水平井水脊耦合模型”(51404201) 史建国(1981 — ),男,工程师,研究方向为油气田开发。 乐平(1983 — ),男,副教授,研究方向为渗流力学与油气藏数值模拟技术。 TE349 A 1673-1980(2017)06-0047-04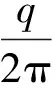
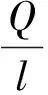
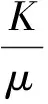


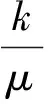
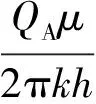
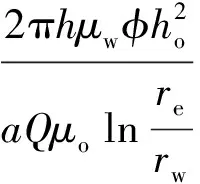
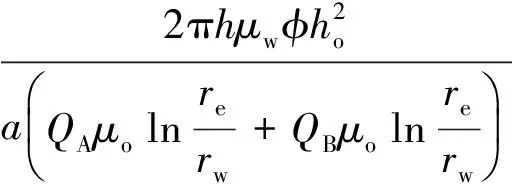
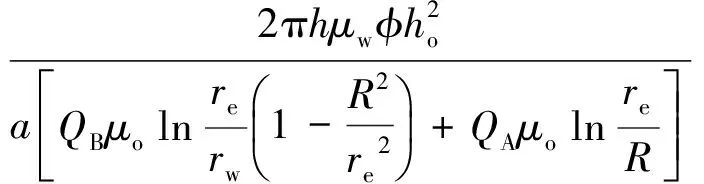
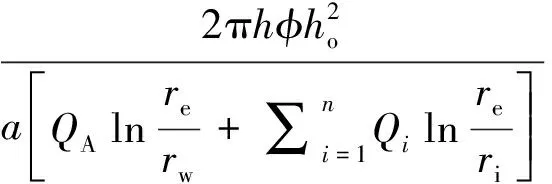
3 实例分析
4 结 语

