直叶桨型科考船艉部振动

，，

(中国舰船研究设计中心，上海 201108)

直叶桨型科考船艉部振动

刘西安，吴广明，李伟杰

(中国舰船研究设计中心，上海 201108)

针对某直叶桨科考船，运用有限元法，参考CCS《船舶振动控制指南》的相关要求，对其艉部区域振动固有频率进行计算，研究甲板板架、船底板架和舱壁板架固有频率计算的边界条件。讨论使用艉部舱段模型计算艉部固有频率的建模范围和附连水施加方法。结果表明，对于甲板，板架垂向建模范围要延伸到二甲板处；船底板架，垂向建模范围要延伸到平台处；横舱壁建模范围在纵向要延伸3个肋位。采用局部舱段模型计算艉部固有频率时，推荐建模范围为1/4船长；流固耦合法和刘易斯法2种附连水施加方法计算结果差异较大，推荐使用流固耦合法。

艉部振动；模态分析；有限元法；附连水质量；流固耦合法

艉部振动是船舶振动的重要组成部分，对艉部振动计算研究对于船舶振动具有重要意义。对于传统船舶而言，推进器位于艉部下方，船舶艉部直接承受由螺旋桨轴承力和表面力引起的振动；船舶艉部舱段也是主机、辅机和传动轴系等机械设备主要布置的区域，机械振动源分布非常密集，因此，船舶艉部受到流体引起的激振力和机械引起的激振力双重作用。然而，为了减小艉部流体阻力，艉部刚度普遍小于中部的刚度，这使艉部更容易出现振动问题。船舶艉部振动[1-4]成为船舶结构工程研究的热点问题之一。

对于直叶浆推进器的船舶，由于船舶特殊的结构形式，船舶底部采用大开口和艉部采用艉部滑道，导致艉部刚度损失的较大；而且对于科考船这类特殊用途的船舶，艉部甲板是科研人员完成科考研究的重要平台，保证科研人员在科考时，船舶艉部整体结构的稳定性是至关重要。因此，准确、合理地预报该类型船舶艉部的振动模态，对于优化船舶结构的动力学特性及避免结构设计中动力学缺陷具有重要意义。

国内外对于船舶振动计算的方法主要包括解析法、数值模拟法和试验法。解析法主要用于研究简单的板、梁及其组合形成的板架结构振动特性；对于简单结构，能够给出相当准确的结果，但是对复杂的船体结构，解析法难以给出准确的计算结果。随着科学技术的进步，计算机技术的飞速发展，以有限元法为主的数值模拟方法，越来越多地被应用于船舶振动的计算，船舶整体模态和局部模态计算结果普遍地被广大的船舶设计者所认可。郭进涛等[5]以某快艇为例，利用ANSYS软件对其艉部的振动特性进行分析，并且对该艇的艉部振动响应进行评估，给出螺旋桨选择的建议。Yucel等[6]通过建立船舶的三维立体有限元模型，分析船体的局部振动和整体振动，比较干湿模态下的船体的固有频率。张新伟等[7]以40万t矿砂船为例，用有限元法对全船和局部的振动性能进行预报，校核该船的振动特性。Kim，Ki-Sun等[8]剖析了传统的基于有限元法的模态分析法分析船体振动的不足之处，提出从振动能力传递的角度出发，通过分析船体振动能量传递和耗散来研究船体的振动。并应用该方法对甲板室的振动进行分析，取得了满意的结果。刘长卿等[9]提出了一种新的艉部计算的模型，艉部详细结构与船体骨架结合的简化有限元模型，以某全回转推进船舶为例，将计算结果与传统的2种模型(艉部详细模型和混合模型)作对比，并且利用试验测试的方法，验证该模型的合理性。近年来，信号处理技术得到了长足的发展，试验测试法[10]已经成为研究船舶振动重要的方法，实测结果被用于理论计算和数值模拟结果的验证。

本文首先校核了板的固有频率，然后对局部板架固有频率计算的边界条件和舱段模型的建模比例问题开展研究。对于甲板板架、船底板架和舱壁板架的局部板架固有频率的计算，采用多个模型，研究边界条件的影响。针对局部舱段模型，研究通过改变建模范围来研究边界条件的影响。并以某直叶桨科考船为例，以混合模型计算为准，采用多个局部舱段模型方案来研究局部舱段模型建模尺度。鉴于附连水质量是影响船体模态的重要因素，应用刘易斯法和流固耦合法施加附连水，研究了艉部振动的附连水施加方法。

1 基本参数

目标船型为直叶型螺旋桨推进科考船，船体艉部为单层底，横骨架式结构，底部有大开口，艉部甲板设有艉部滑道。船舶航区为无限航区，柴油机驱动，双桨船，巡航速度为15 kn，5叶SPV螺旋桨，转速为0～72 r/min，排水量为3 120 t。基本参数见表1。

表1 基本设计参数

2 有限元模型

2.1 模型范围

参照科考船艉部结构设计方案，取全宽、全高范围内的船尾结构建模，长度方向分别取船长的(1/6)L、(1/5)L、(1/4)L、(1/3)L建立详细艉部的三维舱段模型。在混合模型中，舯艏部采用梁模型，由实船的详细结构图可以计算得到梁模型的参数,见表2。

2.2 单元及网格

单元的主要形式有板壳单元、梁单元、质量点单元和刚性连接单元。板壳单元模拟实船结构中的各种板壳结构，以及各种桁材的腹板。以四边形单元为主，长宽比在2∶1以内，在连接、过渡以及曲率变化较大的地方采用少量三角形单元。梁单元主要用于模拟各种纵骨、加强筋、腹板扶强材的面板等，并考虑偏心距的影响。质量点(mass)单元是模拟货物、各种设备、舾装、舱内的油水等质量的。刚性连接单元(rigid)用来连接混合模型中艉部舱段模型和艏部的一维梁模型。通过对单元材质密度的改变保证与实船空船质量一致。将船内主要设备以集中质量单元(mass)的形式施加在节点表现。有限元模型见图1、图2。

图1 底部板架模型

图2 艉部详细模型

2.3 边界条件

在计算板架模态时，分别使用简支约束和固支约束约束板架的四周。在计算艉部舱段模态时，在前端肋位边界处施加约束XYZ方向的位移。混合模型计算艉部舱段模态时，不需要施加约束。

3 板及板架模态分析

3.1 校核标准

依据CCS《船上振动控制指南》，对该科考船的艉部振动进行校核。把艉部振动区域分成3个。

1)螺旋桨脉动压力直接作用区，船底板、板格和舱壁：f01≥3fb=18 Hz，船底板架：f01≥1.3fb=7.8 Hz。

2)非螺旋桨脉动压力直接作用区：船底外板、板格和舱壁板满足下列要求：f01≥2.2fb=13.2 Hz(n=5)。

3)距尾端0.25L范围内，船底外板、板格和舱壁板的频率满足下列要求：f01≥1.5fb=9 Hz(n=5)。

3.2 板的模态校核

对于船体板的模态计算，采用《CCS振动控制指南》提供的船体板的计算公式，典型船体板的固有频率计算结果见表3。

表3 船体板固有频率

3.3 板架的模态校核

使用有限元法对甲板板架、舱壁板架及船底板架的固有频率进行计算。对比不同建模范围和约束条件的板架模型的计算结果，比较各个板架局部模型固有频率与舱段模型、混合模型计算得到的固有频率的误差，研究板架频率模型简化的方法。

3.3.1 甲板板架模态计算

应用不同尺寸的甲板板架的局部模型计算固有频率，并将计算结果与混合模型和艉部舱段模型计算甲板板架频率相比较。在甲板板架的局部模型中，为了模拟实际情况，将支柱、舱壁等简化为简支约束。甲板板架局部模型见图3；计算结果见表4；振动模态见图4。

名称边界条件板架频率/Hz甲板局部模型1固支约束19.23甲板局部模型1简支约束18.49甲板局部模型2固支约束17.00甲板局部模型2简支约束17.01混合模型无16.18艉部详细模型简支约束15.86

3.3.2 船底板板架模态计算

船底板架局部模型见图5。

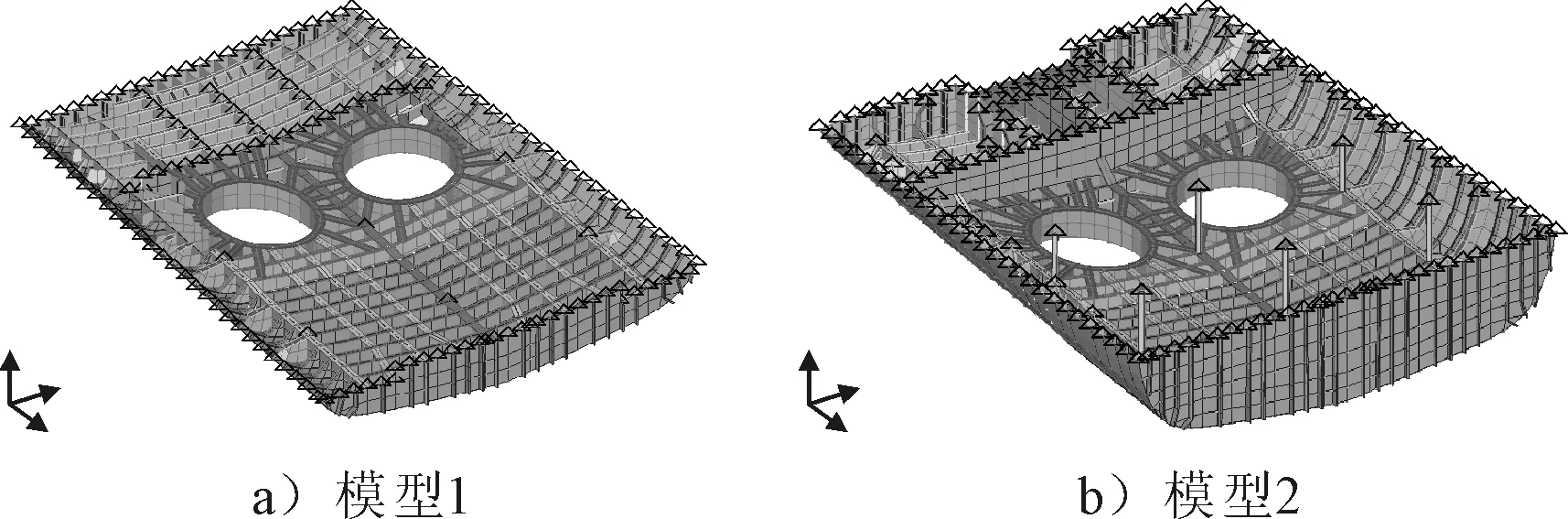
图5 船底局部板架

计算结果见表5，振动见图6。

表5 船底板架频率计算结果

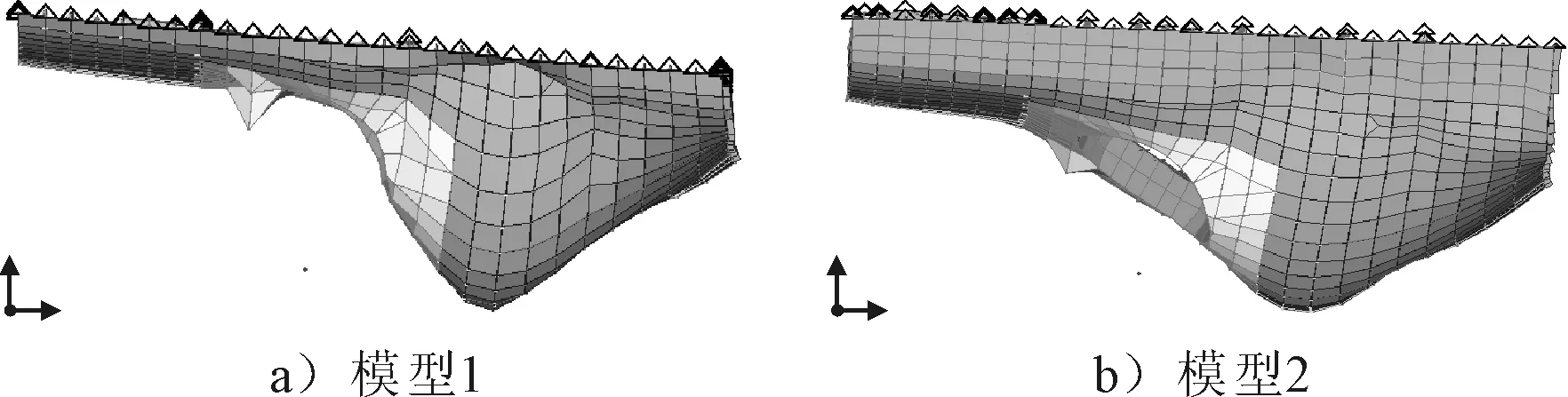
图6 船底局部板架一阶振动

3.3.3 横舱壁板架模态计算

FR16横舱壁板架局部模态计算见图7。

图7 FR16横舱壁板架局部一阶振动

计算结果见表6。

3.3.4 纵舱壁板架模态计算

纵舱壁板架频率计算结果见表7。

各阶模态振型见图8。

由计算结果可知，板和各个板架的振动频率由表8可以看出：均满足规范要求，所以板与板架不会与螺旋桨发生共振。一般将混合模型中计算结果认为是准确的，各个模型相对误差见表8。

表6 FR16横舱壁板架频率计算结果

表7 纵舱壁板架频率计算结果

图8 纵舱壁板架振型

1)采用局部板架模型计算船体板架固有频率时，为了减小边界条件对其影响，要适当扩大建模范围。对于甲板板架的有限元计算模型在垂向延伸到二甲板处；船底板架的有限元计算模型在垂向延伸到邻近的平台处；横舱壁建模范围要向前后延伸至少3个肋位；纵舱壁的建模范围要左右延伸至相邻的纵舱壁或者纵桁处。

表8 频率与误差总结

2)对于船体内部板架结构，横舱壁、纵舱壁和平台等，局部板架模型的约束形式应当采用固支约束；而船体外板架和甲板板架，采用局部板架模型计算固有频率时，边界条件使用简支约束。

4 艉部舱段模态分析

计算船舶艉部舱段振动特性的简化模型主要有2种:一种为仅考虑艉部舱段结构的三维有限元模型，另一种为艉部详细结构和船体梁相结合的混合模型。艉部舱段模型分析艉部振动时，不同的约束条件对其计算结果影响较大。一般情况下船体舱段的约束条件难以确定，因此船舶研究者提出混合模型。该模型既能简化建模工作量，又能避免约束条件对其影响，这种模型应用较为广泛，且计算结果相对准确。然而研究表明，当选择合适的艉部舱段模型时，也能较为准确地反映出船舶艉部振动特性。因此，研究舱段模型建模范围对于简化建模工作和提高计算效率具有重要意义。研究舱段模型建模方案见表9。

表9 局部舱段模型研究方案

另外，计算船体艉部的振动模态，必须考虑附连水对其的影响。传统计算附连水质量的方法为刘易斯法，通过公式计算各阶附连水质量，然后通过改变结构密度或者施加质量单元MASS模拟。随着计算机技术的飞速发展，其与计算力学的结合日益紧密。应用流体单元模拟舷外水与船体相互耦合的方法计算船体振动模态的方法被广泛接受，流固耦合的方法也开始应用于计算船体湿模态。结合上述论述，在计算船舶艉部频率时，分别应用刘易斯法和流固耦合法，比较不同的附连水施加方法对计算结果的影响。流固耦合法是通过定义流体和固体相互作用的耦合面,来模拟船舶在水中自由振动时舷外水对其的影响。在NASTRAN中，通过定义船体湿表面积、流体密度和吃水来施加附连水质量。

流固耦合法艉部舱段模型、刘易斯法艉部舱段模型与流固耦合法混合模型见图9～11。通过研究不同尺寸的舱段模型，总结出舱段模型合理的建模范围。

图9 流固耦合法艉部舱段模型

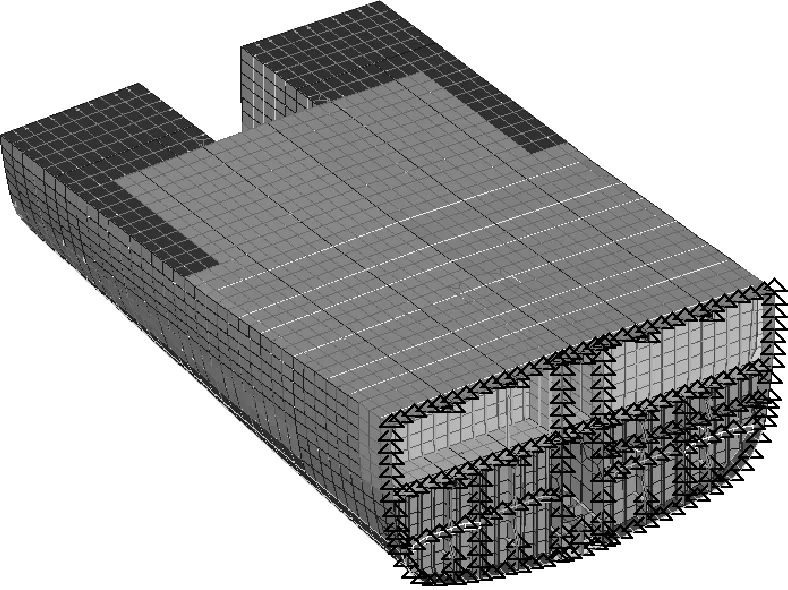
图10 刘易斯法艉部舱段模型

图11 流固耦合法的混合模型

研究不同尺寸的舱段模型，应用不同附连水施加方法计算得到的各个模型频率与混合模型的流固耦合法的相对误差见表10。

表10 各个模型模态计算结果及相对误差汇总

注：L-刘易斯法施加附连水；F-流固耦合法施加附连水。

由表10，可以得到如下结论：

1)研究发现，不同的舱段模型计算得到的结果差异较大，而且，随着建模范围的增大，模态频率在减小，这主要反应了边界条件对模型结果的影响。当舱段模型建模范围恰好选择为船体梁第一阶振动节点附近时，这时候模态计算的结果与混合模型计算结果吻合度较好。方案3的模型范围在振动节点附近，频率计算结果与混合模型计算结果误差很小，控制在5%左右。因此，在选用艉部舱段模型时，本文推荐(1/4)L舱段模型建模范围。

2)舱段模型中，刘易斯法和流固耦合法2种方法计算结果的差异较大。这说明，在使用舱段模型研究结构振动时，局部振动的附连水施加方法和总体振动的附连水施加方法是不一致的。流固耦合法是将船体作为弹性体，通过流体与结构之间相互影响耦合作用，反应出船体振动情况。所以，研究局部舱段振动时，推荐使用虚拟质量的方法考虑附连水的影响。

3)刘易斯法和流固耦合法在使用混合模型计算船体模态时，低阶振动频率吻合较好，但是高阶和扭转模态频率吻合较差，特别是扭转，误差在10%以上。这是因为，在低阶时刘易斯法能够反映附连水的质量，但是随着阶数的增加，误差越来越大；另外，刘易斯法没有计算弯曲-扭转耦合振动的附连水质量公式，而是通过水平附连水质量公式进行代替，这也导致振动计算的结果差异较大。

5 结论

该科考船的板、板架和舱段模态频率的计算结果满足CCS《船上振动控制指南》要求。

在使用板架局部模型计算板架模态频率时，计算结果表明，当板架建模范围满足一定的要求时，可以减小边界条件对计算结果的影响，对于甲板板架的有限元计算模型在垂向延伸到二甲板处；船底板架的有限元计算模型在垂向延伸到邻近的平台处；横舱壁建模范围要向前后延伸至少3肋位；纵舱壁的建模范围要左右延伸至相邻的纵舱壁或者纵桁处；船体板架中，由于板架所处的位置不同，边界条件的约束形式也不同，外板板架和甲板板架采用简支约束，横舱壁、纵舱壁和平台板架采用固支约束。该结论适用于其他船型。

在舱段模态研究中，分析了不同舱段模型建模范围对计算结果影响，研究表明，当舱段建模范围恰好取在节点振动的附近时，该舱段模型模态计算结果与混合模型计算结果吻合度较好，这为我们在使用舱段模型计算船舶艉部振动时，提供了舱段模型的建模范围。对于该类型的船舶，推荐(1/4)L舱段模型建模范围。

在研究不同方法施加附连水对模态频率的影响时，结果表明：刘易斯法和流固耦合法用于计算船舶总体振动的低阶的计算结果相差不大，而在计算局部振动时的结果差异较大。流固耦合法可以较为真实地模拟船体在水中振动的实际情况，并比较准确地反应附连水质量分布，更能准确地计算船体振动的模态频率。因此，在局部振动分析时，采用流固耦合法施加附连水质量。另外，对于局部板架频率计算，如果能够采用弹性边界来模拟，可以进一步提高计算的精确度；对于舱段模型计算艉部频率采用(1/4)L模型，具有一定的局限性，是否能够推广到其他船型还需进一步研究。

[1] 董良雄,张涛,温小飞,等.船舶艉部结构对尾轴振动特性影响研究[J].船舶工程,2016(10):72-75.

[2] 韩正君,梁程诚,梅永娟.带尾滑道船型艉部结构振动固有特性分析[J].船舶与海洋工程,2015(4):26-29.

[3] 梅永娟,曹志岗,杨德庆,等.改装舰艇艉部振动数值预报方法[J].噪声与振动控制,2013(2):173-177.

[4] 冯国平,谌勇,黄修长,等.舰艇艉部纵向激励传递特性分析[J].噪声与振动控制,2009(6):132-135.

[5] 郭进涛,胡要武,董威.基于ANSYS的快艇艉部结构振动响应分析[J].中国水运(下半月),2015(7):4-6,24.

[6] Yucel, Adil1, Arpaci, Alaeddin2. Analysis of free and forced ship vibrations using finite element method[C]. ASME 2010 10th Biennial Conference on Engineering Systems Design and Analysis, ESDA2010,2010.

[7] 张新伟,吴小康,陆利平.40万t矿砂船全船和局部振动研究[J].中国造船,2011(1):26-38.

[8] Kim, Ki-Sun, Heui-Won. Vibration control for ship’s deck house using vibration intensity analysis method[C]. 42nd International Congress and Exposition on Noise Control Engineering 2013, INTER-NOISE 2013: Noise Control for Quality of Life,2013,6:4515-4521.

[9] 刘长卿,车驰东,闫菲.船舶艉部模态数值计算与测试[J].船舶力学,2016(4):478-486.

[10] 傅仁华,刘镇,黄映云.某船船体模态及振动测试[J].船海工程,2007(3):14-17.

Vibration Modal Analysis of Stern Structure for Scientific Research Ship with VSP

LIUXi-an,WUGuang-ming,LIWei-jie

(China Ship Design and Research Centre, Shanghai 201108, China)

The stern natural frequency of the scientific research ship with VSP was checked with FEM, referring to the relevant requirement of the CCS Guide for Ship Vibration Control. The influence of boundary conditions were discussed when the natural frequency of deck plate, bottom plate rack and bulkhead frame were calculated. Different stern cabin models were used to analyze the impact of modeling range on the natural frequency. Lewis method and virtual mass method were both used to consider the influence of outside water upon the wet modal. The results showed that the range FEM of deck rank extended to the second deck in vertical. The range of bottom rank extended to near deck in vertical. The range of bulkhead frame extended to 3 frame-spaces in longitudinal. When the stern cabin model was used to analyze the natural frequency, the reasonable range of the local FEM was 1/4L. The result of the stern cabin model applying the added mass by Lewis method was different greatly from that by fluid-structure interaction method, and the latter was recommended.

stern vibration; modal analysis; additional water mass; FEM; fluid-structure interaction

U661.44

A

1671-7953(2017)06-0032-06

10.3963/j.issn.1671-7953.2017.06.007

2017-03-01

2017-04-13

刘西安(1991—)，男，硕士生

研究方向：船舶振动噪声，结构强度