考虑焊接残余应力的船体板结构屈曲强度

，，

(1.海军工程大学 动力工程学院，武汉 430033；2.91404部队，河北 秦皇岛 066001)

考虑焊接残余应力的船体板结构屈曲强度

刘伯运1，周晓松1，张岳林2

(1.海军工程大学 动力工程学院，武汉 430033；2.91404部队，河北 秦皇岛 066001)

传统的船体板结构屈曲计算模型一般为完整板格模型，但在实际中焊接残余应力的影响是不可避免的。针对这一问题，基于有限元热-力顺序耦合方法，计算加筋板在单轴压缩载荷下的屈曲特征值，结果表明纵筋间距越大，焊接残余应力对加筋板稳定性的影响越大；纵筋长细比越大，焊接残余应力对加筋板稳定性的影响越小。与Recking No.23模型试验对比，验证了热-力顺序耦合方法的有效性和应用价值。

焊接残余应力；加筋板；屈曲强度；热-力顺序耦合；单轴压缩

船体结构是典型的薄壁结构，其主要由加筋板组成，对于此类结构，尤其是在疲劳裂纹萌生之前，其压缩强度往往比拉伸强度更值得关注[1-2]。随着板壳稳定性理论的逐步完善和有限元数值计算能力的不断提高，完整加筋板结构的屈曲强度研究日渐成熟。例如，王伟等[3]利用解析法对加筋板稳定性进行了研究，忽略材料非线性的影响，利用理论方法求解了四边简支加筋板的整体屈曲临界应力；张涛等[4]分析了加筋板非线性屈曲与后屈曲，采用离散加筋板模型,忽略筋截面上的剪切应力,引入板和筋的应力函数,得到了加筋板屈曲的非线性控制方程；曹健[5]基于油船结构共同规范，对屈曲强度进行了直接计算。然而，在建造过程中，加筋板结构不可避免的产生几何变形和残余应力，尤其像船舶这类用焊接连接的钢结构，要完全消除结构的残余应力是不可能的。在焊接钢结构中，在焊缝附近有达到材料屈服极限的残余拉伸应力，与之相平衡的在离焊缝较远处有残余压缩应力[6]。文献[6]还指出，在焊接构件中，焊接导致集中的局部热输入，引起不断变化的不均匀温度场，产生塑性变形。冷却以后，在远离焊缝部位产生压应力，而在焊缝处产生拉应力，由焊接引起的残余应力要比型钢中大得多。可见，船体结构的稳定性不仅取决于船体构件的形状、尺度、材料特性，而且在很大程度上受到焊接残余应力的影响，因此，在结构的屈曲强度分析中要充分考虑。本文将探讨利用有限元法模拟焊接残余应力的方法，进而基于热-力顺序耦合，得到含残余应力加筋板屈曲失稳的一般规律。

1 焊接残余应力的数值模拟

钢材的焊接是一个不均匀加热的过程：焊缝区金属受到电弧加热，迅速升温达到熔化温度，而离电弧较远的金属温度明显较低，仍然接近室温。在ABAQUS中，这种焊接过程可以用热应力分析的方法来模拟，模型产生一定的几何变形和残余应力。具体步骤如下。

1)试验模型的焊缝位于船体板、骨材、肋板等构件的连接处。材料采用E36钢，其弹性模量、热膨胀系数、比热容、热传导系数等物理量与温度的关系见图1[7]。在初始步，所有焊缝处节点的温度等于室温T0=20 ℃。

图1 材料属性

2)定义一个加热步。焊缝节点瞬间升高到1 500 ℃，这是船厂常用的焊接温度。调节焊接加热区域的范围，控制残余应力的大小。焊缝区金属受热膨胀，而四周钢板阻止它的膨胀，从而焊缝区产生压缩应力。当压缩应力超过材料的屈服强度时，焊缝附近的金属产生压缩性的塑性变形。

3)定义一个冷却步。焊缝节点逐渐冷却至室温T0=20 ℃，焊缝区金属开始降温收缩。此时，焊缝的收缩又受到四周钢板的限制，从而焊缝区出现拉应力。整个模型结构是一个内力平衡系统，非焊缝区就会产生压应力来平衡焊缝区的拉应力。焊缝降到室温，试验模型就产生了焊接残余应力和相应的初始几何变形。

以含3根纵筋的船体板为例，材料的杨氏模量E=210 GPa，泊松比μ=0.3，线胀系数1.35×10-5℃-1，使用S4R(4节点双曲线缩减积分壳单元)，划分网格2 016个，见图2。

图2 载荷、边界条件的施加和网格的划分

热应力分析结束之后，试验模型的初始变形和沿板长方向的焊接残余应力见图3。船体外板的平均压缩应力为91.57 MPa，接近文献[8]给出的结果91 MPa，这个数值位于0.15σy和0.3σy之间，达到ISSC[9]规定的焊接残余应力的平均水平。

图3 焊接残余应力云图

2 板壳稳定性基本理论

薄板的线性屈曲分析实际上是无横向载荷作用，在中面力作用下板的弯曲。由平面应力问题求得的板单元的中面力Nx、Ny和剪力Nxy，在板的弯曲过程中，认为中面内力保持不变。薄板单元的中面位能为

即

若采用有限元求解，单元内的位移场为

w=Nu

式中：N、u分别为单元的形函数和节点位移向量。

式中几何刚度矩阵

而H为薄板单元中面力矩阵，其定义为

对于受压结构，随着压应力的增加，结构抵抗横向变形的能力会下降。当载荷大到某一水平，结构总体刚度变为零，丧失稳定性。屈曲分析研究失稳发生时的临界载荷和失稳形态。若采用有限元法求板结构失稳发生时的临界载荷和失稳形态，则其有限元方程为

(K0+λkσ)U=0

式中：K0=∑K0，kσ=∑kσ分别为板结构的弯曲刚度矩阵和几何刚度矩阵；k0为不考虑中面力影响的单元弯曲刚度矩阵；U为板结构的位移向量；λ为屈曲失稳临界载荷因子，K0中已经施加了合适的边界条件。基于失稳时结构系统刚度矩阵会出现奇异，所以可将失稳问题转化成特征值问题处理。

求解板稳定的特征方程为

|K0+λKσ|=0

可用Power Sweep(反迭代法)和Lanczos向量法求解特征值[10]，求出最小的特征值λ1和相应的特征向量后，λ1Nx,λ1Ny,λ1Nxy便是临界中面力，特征向量是板的屈曲形式。

3 含残余应力的加筋板稳定性

热变形工件内部的塑性变形和传热发生在同一空间域和时间域，但由于变形与传热二者属于不同物理性质的问题，分别由弹塑性问题和瞬态热传导问题描述，因此，其对应场量难以采用联立求解的方法分析。一般而言，弹塑性有限元法采用增量法逐步解出工件的有关场量，而温度场则利用时间差分格式逐步积分得到。这样可以在某一瞬时分别计算变形和温度，通过二者之间的联系，将它们的相互作用考虑进去，以达到焊接热力过程的耦合分析。耦合分析是指在有限元分析的过程中考虑了两种或者多种物理场的交叉作用和相互影响。

耦合场的分析可归结为直接耦合(Fully coupling)、间接耦合(Co-simulation)和顺序(Sequential)耦合3种，其中顺序耦合是把间接耦合的多物理场同步协同求解，演变成多物理场多步顺序求解，其应用范围最广，比较适用于含焊接残余应力结构的强度计算，其操作流程见图4。

图4 顺序耦合操作流程

3.1 纵筋间距的影响

取3组算例，每组加筋板纵筋间距c的变化范围为0.25b～b(其中b为板宽)，加筋板四边简支，在板宽和纵筋截面上施加单位壳边载荷(shell edge load)，以c=0.33b为例，含焊接残余应力的加筋板前4阶屈曲模态见图5，当β=0.33时，不同纵筋间距的加筋板第1阶屈曲模态见图6。

图5 加筋板前4阶屈曲模态

图6 不同纵筋间距的加筋板屈曲模态

用Dπ2/hb2量纲一的量化临界应力，得到临界载荷系数k，填入表1、表2中，以表征加筋板的稳定性。

理想加筋板和含焊接残余应力加筋板临界载荷系数随纵筋间距的变化，见图7，由焊接残余应力引起的强度减弱见图8。

表1 加筋板临界载荷系数(β=0.11)

表2 加筋板临界载荷系数(β=0.33)

图7 临界载荷系数随纵筋间距的变化

图8 焊接缺陷加筋板临界载荷系数的减弱

可以看出，加筋板在单轴压缩载荷下，屈曲强度大体上随纵筋间距的增大而减小，减小的程度逐渐减小，特别的，c/b=0.5时的临界载荷系数小于c/b=1的情况，这是因为当c/b=1时，纵筋恰好位于加筋板失稳半波的波峰处，如图6a)所示。这提示我们加筋板屈曲强度不仅与纵筋间距有关，而且很大程度上取决于加强筋的位置。在工程设计中，合理设计纵筋的位置，能在提高加筋板稳定性的基础上节省材料。

观察图8，相对于理想加筋板，焊接加筋板屈曲强度减弱的程度基本上随纵筋间距的增大而增大，即纵筋间距越大，焊接残余应力对加筋板稳定性的影响越大。然而，当c/b=0.5，β=0.33时，焊接加筋板屈曲强度减弱百分比为负值，即焊接加筋板的屈曲强度反而比完整加筋板大。这是因为焊接残余应力的方向与板屈曲失稳的方向相反，即在少数情况下，焊接残余应力能起到良性作用，如利用表面感应淬火技术使工件表面产生残余压应力，抵消工作载荷所产生的一部分拉应力，从而显著提高工件弯曲疲劳抗力和扭转疲劳抗力[11]。

3.2 纵筋截面参数的影响

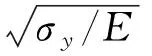
理想加筋板和焊接加筋板临界载荷系数随纵筋长细比的变化见表4和图10。由图10可知，加筋板临界载荷系数随纵筋长细比的增大而增大，当β=0.56时达到最大。由图9e)可知，此时加筋板的失稳模式为板结构整体失稳，继续增大加强筋长细比，板结构屈曲强度开始减小，此时由于纵筋自由边离开与板材连接边的距离增大，纵骨比板材更容易失稳。可见，在工程设计中，纵筋长细比应不大于0.56，否则将失去扶强作用。

图9 屈曲模态随纵筋长细比的变化(r=3)

βIntactpanelWeldedpanelDegradation/%0.113.182.7314.050.224.143.759.360.336.516.263.900.4510.1510.100.460.5611.4611.450.080.6711.4111.410.05

表4 加筋板临界载荷系数随纵筋长细比的变化(r=3)

图10 加筋板临界载荷系数随纵筋长细比的变化

此外，对比图10中r=1和r=2两条曲线(或对比r=3和r=4两条曲线)，我们发现两条曲线在β=0.45之前几乎是重合的。可见在工程设计中，当纵筋长细比大于0.45时，增加加强筋的数目对提高加筋板的屈曲强度才更为显著。

由焊接引起的加筋板屈曲强度减弱见图11。可见，随着纵筋长细比的增大，焊接残余应力对加筋板屈曲强度的影响逐渐减小。

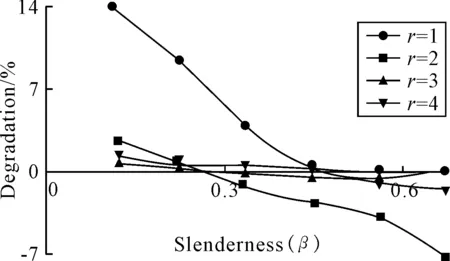
图11 由焊接引起的加筋板稳定性减弱

4 算例分析

4.1 模型概述

本文采用Reckling No.23模型[12]进行计算分析，模型具体参数见图12。

其中模型的长度L=500 mm，甲板板、底板、边板、角钢和扁钢的厚度均为2.5 mm，材料屈服极限为246 MPa，E=210 GPa，泊松比μ=0.3，线胀系数1.35×10-5。

图12 模型参数

4.2 计算分析

建立ABAQUS有限元模型，见图13。赋予截面属性，设置static,general和buckle分析步，创建参考点以及参考点与端面间的耦合约束，见图14。在初始分析步定义温度场，在buckle分析步创建端面简支边界条件，在参考点上施加单位大小的端部弯矩，使用S3(3节点有限薄膜应变壳单元)，划分网格4 240个，见图15。焊接残余应力云图见图16。由图17可知，第1阶屈曲模态屈曲特征值为2.13×108，与试验值2.36×108N·mm较为接近，相对误差为5.5%。

图13 有限元模型

图14 耦合约束

图15 划分网格

图16 焊接残余应力云图

图17 屈曲模态

5 结论

1)无论是否考虑焊接残余应力，加筋板临界载荷系数都随纵筋长细比的增大而增大，当β=0.56时达到最大，此时若继续增大纵筋长细比不再具有工程意义。

2)纵筋间距越大，焊接残余应力对加筋板稳定性的影响越大，纵筋长细比越大，焊接残余应力对加筋板稳定性的影响越小。

3)在少数情况下，焊接残余应力与构件工作应力方向相反，残余应力起到良性作用。

4)除纵筋间距和长细比外，焊接加筋板的稳定性还与纵筋位置有关，有待进一步深入研究。

[1] Mohammad. Strength of steel plates with both-sides randomly distributed with corrosion wastage under uniaxial compression[J]. Thin-walled structures,2011,49:325-342.

[2] JIANG Xiaoli, C. Guedes Soares. A closed form formula to predict the ultimate capacity of pitted mild steel under biaxial compression[J]. Thin-walled structures,2012,50:27-34.

[3] 王伟,吴梵.加筋板整体屈曲临界应力计算与分析[J].中国舰船研究，2011(3)：21-27.

[4] 张涛,刘土光,赵耀,等.初始缺陷加筋板的屈曲与后屈曲分析[J].船舶力学，2003(1)：79-83.

[5] 曹健.基于油船结构共同规范的屈服与屈曲强度直接计算研究[D].哈尔滨：哈尔滨工程大学，2007.

[6] 束长庚,周国华.船舶结构的屈曲强度[M].北京:国防工业出版社,2006.

[7] 陈哲超，陈震.加筋板结构连续焊焊接变形规律[J].中国舰船研究，2016(3)：68-73，88.

[8] 师桂杰.集装箱船船体结构极限强度研究[D].上海：上海交通大学，2011.

[9] ISSC. Proceedings of the 17th international ship and offshore structures congress[C].Korea,2009.

[10] XIANYI Z. Numerical calculating method and fortran language[M]. Beijing: Electrical Industry Press,1986.

[11] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.

[12] RECKLING K A. Behavior of box girder under bending and shear[C]. Proc. ISSC, Paris 1997.

On Buckling Strength of Hull Plates in the 砂船分体式供气的风险Presence of Welding Residual Stress

LIUBo-yun1,ZHOUXiao-song1,ZHANGYue-lin2

(1.Dept. of Power Engineering, Naval University of Engineering, Wuhan 430033, China;2.No.91404 Unit of PLA, Qinhuangdao Hebei 066001, China)

To calculate the stability of hull plate structures in the presence of welding residual stress, the buckling mechanism of stiffened panels under uniaxial compressive load was researched by using FE thermal-force sequential coupling method. The results showed that the influence of welding residual stress upon stability of stiffened panels increases with the incretion of longitudinal spacing and decreases with longitudinal slenderness. Compared with experimental results of Recking No.23 model, the validity and application value of the FE sequential coupling method was verified.

welding residual stress; stiffened panel; buckling strength; sequential coupling; uniaxial compression

U661.43

A

1671-7953(2017)06-0006-06

10.3963/j.issn.1671-7953.2017.06.002

2017-03-06

2017-04-16

国家自然科学基金(51479205)

刘伯运(1977—)，男，博士，副教授

研究方向：舰艇结构系统安全性